深度生成模型:DCGAN与Wasserstein GAN公式深度推导
深度卷积生成对抗网络 DCGAN
在原始 GAN 框架中,生成器和判别器通常使用全连接层构建,这限制了模型处理图像的能力。为此,Radford 等人在 2016 年提出了 DCGAN(Deep Convolutional GANs),将 CNN 架构引入 GAN 系统,在图像生成任务中取得巨大成功。
DCGAN 的网络结构

DCGAN 仍然包括两个模块:
生成器(Generator):
- 输入为一个随机向量 z z z,通常为 z ∼ N ( 0 , 1 ) z \sim \mathcal{N}(0, 1) z∼N(0,1);
- 通过一系列反卷积(Fractional Strided Convolutions / Transposed Convolutions)层将低维噪声向量逐步上采样为图像;
- 输出图像维度如 64 × 64 × 3 64 \times 64 \times 3 64×64×3。
判别器(Discriminator):
- 接收图像(真实或伪造)作为输入;
- 通过一系列普通卷积(strided convolutions)和 LeakyReLU 激活函数进行下采样;
- 最后输出一个标量,表示输入图像为“真实图像”的概率。
图中展示了典型 DCGAN 结构:
- 左侧:生成器网络,逐步上采样生成图像;
- 右侧:判别器网络,逐步提取图像特征进行判断;
- 右上角还展示了反卷积(Transposed Convolution)过程,直观说明如何将小尺寸特征图恢复成大尺寸图像。
DCGAN 的设计原则(五条黄金法则)
去除所有池化层(Pooling):
strided convolutions (discriminator) and fractional-strided convolutions (generator)
在生成器中使用 Fractional Strided Convolution(即反卷积)进行上采样;
在判别器中使用 Strided Convolution 进行下采样。
在生成器和判别器中都使用 Batch Normalization:
- 有助于稳定训练;
- 防止梯度消失;
- 加速收敛。
移除所有全连接隐藏层(fully-connected hidden layers):
- 简化网络结构;
- 提升可扩展性与泛化能力。
激活函数设计:
- 在生成器中,除了最后一层使用 Tanh,其余各层都使用 ReLU 激活;
- 在判别器中,所有层都使用 LeakyReLU 激活,避免死神经。
输出范围规范化:
- 生成器输出图像通过 Tanh 映射到 [ − 1 , 1 ] [-1, 1] [−1,1];
- 因此训练图像也需要归一化处理至 [ − 1 , 1 ] [-1, 1] [−1,1]。
总结
DCGAN 通过引入卷积结构,使得 GAN 在图像领域具备更强建模能力:
- 支持大尺寸图像生成;
- 图像更加平滑、连贯、有结构;
- 训练更稳定,调参更容易;
- 为后续诸如 StyleGAN、Pix2Pix 等强大 GAN 模型奠定了基础。
来源于 Radford 等人发表于 ICLR 2016 的经典论文:
“Unsupervised Representation Learning with Deep Convolutional GANs”
GAN 的核心训练难题:梯度消失(Gradient Vanishing)
尽管 DCGAN 等架构提升了稳定性,但生成对抗网络在训练早期仍然面临一个经典难题:梯度消失问题(vanishing gradient)。
原始目标函数
判别器的训练目标为:
J ( D ) = − E x ∼ p r [ log D ( x ) ] − E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(D)} = -\mathbb{E}_{x \sim p_r}[\log D(x)] - \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(D)=−Ex∼pr[logD(x)]−Ex∼pg[log(1−D(x))]
生成器的训练目标为:
J ( G ) = E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(G)} = \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(G)=Ex∼pg[log(1−D(x))]
生成器尝试最大化 D ( G ( z ) ) D(G(z)) D(G(z)),使得判别器误判其为真实图像。
为什么会发生梯度消失?
在训练初期,生成器 G G G生成的图像往往非常粗糙,不具备真实数据的特征。此时:
- 判别器 D D D很容易分辨出 G ( z ) G(z) G(z)是伪造的;
- 因此 D ( G ( z ) ) ≈ 0 D(G(z)) \approx 0 D(G(z))≈0;
- 那么 log ( 1 − D ( G ( z ) ) ) ≈ 0 \log(1 - D(G(z))) \approx 0 log(1−D(G(z)))≈0,梯度也几乎为零;
- 生成器难以获得有效的梯度信号进行优化。
本质悖论
In GAN, better discriminator leads to worse vanishing gradient in its generator!
- 判别器越强,训练越快,越容易压垮生成器;
- 生成器越弱,收到的训练信号越微弱;
- 双方很难在初期同步进步,导致训练不稳定。
1. 原始 GAN 判别器的最优目标函数推导
我们先从 GAN 中判别器 D D D 的原始损失函数出发:
J ( D ) = − E x ∼ p r [ log D ( x ) ] − E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(D)} = -\mathbb{E}_{x \sim p_r}[\log D(x)] - \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(D)=−Ex∼pr[logD(x)]−Ex∼pg[log(1−D(x))]
这是判别器试图最大化其“判断正确”的期望值:
- 第一项:希望对真实样本 x ∼ p r x \sim p_r x∼pr 输出 D ( x ) D(x) D(x) 尽可能大(接近 1);
- 第二项:希望对生成样本 x ∼ p g x \sim p_g x∼pg 输出 D ( x ) D(x) D(x) 尽可能小(接近 0)。
我们将 J ( D ) J^{(D)} J(D) 看作对 D ( x ) D(x) D(x) 的函数,在每个点 x x x 上独立求偏导并令其为 0,即可求出最优判别器。
2. 最优判别器 D ∗ ( x ) D^*(x) D∗(x) 的解析表达式
当 J ( D ) J^{(D)} J(D) 取极大值时,对每个 x x x,最优解满足:
∂ J ( D ) ∂ D ( x ) = − p r ( x ) D ( x ) + p g ( x ) 1 − D ( x ) = 0 \frac{\partial J^{(D)}}{\partial D(x)} = -\frac{p_r(x)}{D(x)} + \frac{p_g(x)}{1 - D(x)} = 0 ∂D(x)∂J(D)=−D(x)pr(x)+1−D(x)pg(x)=0
d d x log x = 1 x \frac{d}{dx} \log x = \frac{1}{x} dxdlogx=x1
解该方程可得:
D ∗ ( x ) = p r ( x ) p r ( x ) + p g ( x ) D^*(x) = \frac{p_r(x)}{p_r(x) + p_g(x)} D∗(x)=pr(x)+pg(x)pr(x)
这表明,最优判别器会根据两个分布的相对概率密度比值来输出真实的可能性概率。
例如:
- 若 p r ( x ) ≫ p g ( x ) p_r(x) \gg p_g(x) pr(x)≫pg(x),说明该点 x x x 更可能来自真实数据, D ∗ ( x ) → 1 D^*(x) \to 1 D∗(x)→1;
- 若 p g ( x ) ≫ p r ( x ) p_g(x) \gg p_r(x) pg(x)≫pr(x),说明该点更可能是伪造的, D ∗ ( x ) → 0 D^*(x) \to 0 D∗(x)→0;
- 若两者相等, D ∗ ( x ) = 0.5 D^*(x) = 0.5 D∗(x)=0.5,即判别器无法判断。
3. 生成器目标函数下的 JS 散度
在 GAN 中,生成器的原始损失为:
J ( G ) = E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(G)} = \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(G)=Ex∼pg[log(1−D(x))]
若将最优判别器 D ∗ ( x ) D^*(x) D∗(x) 代入,可得生成器最小化的目标函数为:
J ( G ) = E x ∼ p g [ log ( 1 − p r ( x ) p r ( x ) + p g ( x ) ) ] = E x ∼ p g [ log ( p g ( x ) p r ( x ) + p g ( x ) ) ] J^{(G)} = \mathbb{E}_{x \sim p_g} \left[\log\left(1 - \frac{p_r(x)}{p_r(x) + p_g(x)}\right)\right] = \mathbb{E}_{x \sim p_g} \left[\log\left(\frac{p_g(x)}{p_r(x) + p_g(x)}\right)\right] J(G)=Ex∼pg[log(1−pr(x)+pg(x)pr(x))]=Ex∼pg[log(pr(x)+pg(x)pg(x))]
该函数与下面这个表达式一同构成 GAN 最优判别器目标:
J ( D ∗ ) = 2 J S ( p r ∥ p g ) − 2 log 2 J^{(D^*)} = 2\,JS(p_r \| p_g) - 2\log 2 J(D∗)=2JS(pr∥pg)−2log2
即,在 D = D ∗ D=D^* D=D∗ 时,GAN 的优化等价于最小化真实分布 p r p_r pr 与生成分布 p g p_g pg 之间的 Jensen-Shannon 散度(JS divergence)。
4. Jensen-Shannon 散度的定义
JS 散度是衡量两个概率分布相似度的一种对称度量方式,定义为:
J S ( p ∥ q ) = 1 2 K L ( p ∥ m ) + 1 2 K L ( q ∥ m ) JS(p \| q) = \frac{1}{2}KL(p \| m) + \frac{1}{2}KL(q \| m) JS(p∥q)=21KL(p∥m)+21KL(q∥m)
其中, m ( x ) m(x) m(x) 是 p p p 和 q q q 的平均分布:
m ( x ) = 1 2 ( p ( x ) + q ( x ) ) m(x) = \frac{1}{2}(p(x) + q(x)) m(x)=21(p(x)+q(x))
而 KL 散度(Kullback-Leibler Divergence)为:
K L ( p ∥ q ) = − ∑ x p ( x ) log ( q ( x ) p ( x ) ) KL(p \| q) = -\sum_x p(x) \log\left(\frac{q(x)}{p(x)}\right) KL(p∥q)=−x∑p(x)log(p(x)q(x))
特性:
- JS 散度值域在 [ 0 , log 2 ] [0, \log 2] [0,log2];
- JS 散度为 0 当且仅当 p = q p = q p=q;
- 若 p p p 和 q q q 的支持集无交集,则 J S ( p ∥ q ) = log 2 JS(p \| q) = \log 2 JS(p∥q)=log2;
- JS 散度的梯度在边界处为 0,这会导致训练困难(梯度消失)。
推导说明:为什么有
V ( D ∗ , G ) = K L ( p r ∥ m ) + K L ( p g ∥ m ) − 2 log 2 V(D^*, G) = KL(p_r \| m) + KL(p_g \| m) - 2 \log 2 V(D∗,G)=KL(pr∥m)+KL(pg∥m)−2log2
背景:我们从最优判别器的对抗损失出发:
V ( D ∗ , G ) = E x ∼ p r [ log ( p r ( x ) p r ( x ) + p g ( x ) ) ] + E x ∼ p g [ log ( p g ( x ) p r ( x ) + p g ( x ) ) ] V(D^*, G) = \mathbb{E}_{x \sim p_r} \left[ \log \left( \frac{p_r(x)}{p_r(x) + p_g(x)} \right) \right] + \mathbb{E}_{x \sim p_g} \left[ \log \left( \frac{p_g(x)}{p_r(x) + p_g(x)} \right) \right] V(D∗,G)=Ex∼pr[log(pr(x)+pg(x)pr(x))]+Ex∼pg[log(pr(x)+pg(x)pg(x))]关键技巧:定义中间分布:
m ( x ) = 1 2 ( p r ( x ) + p g ( x ) ) ⇒ p r ( x ) + p g ( x ) = 2 m ( x ) m(x) = \frac{1}{2}(p_r(x) + p_g(x)) \quad \Rightarrow \quad p_r(x) + p_g(x) = 2m(x) m(x)=21(pr(x)+pg(x))⇒pr(x)+pg(x)=2m(x)换分母:
p r ( x ) p r ( x ) + p g ( x ) = p r ( x ) 2 m ( x ) , p g ( x ) p r ( x ) + p g ( x ) = p g ( x ) 2 m ( x ) \frac{p_r(x)}{p_r(x) + p_g(x)} = \frac{p_r(x)}{2m(x)}, \quad \frac{p_g(x)}{p_r(x) + p_g(x)} = \frac{p_g(x)}{2m(x)} pr(x)+pg(x)pr(x)=2m(x)pr(x),pr(x)+pg(x)pg(x)=2m(x)pg(x)带入期望后:
V ( D ∗ , G ) = E x ∼ p r [ log ( p r ( x ) 2 m ( x ) ) ] + E x ∼ p g [ log ( p g ( x ) 2 m ( x ) ) ] V(D^*, G) = \mathbb{E}_{x \sim p_r} \left[ \log \left( \frac{p_r(x)}{2m(x)} \right) \right] + \mathbb{E}_{x \sim p_g} \left[ \log \left( \frac{p_g(x)}{2m(x)} \right) \right] V(D∗,G)=Ex∼pr[log(2m(x)pr(x))]+Ex∼pg[log(2m(x)pg(x))]拆开 log \log log 用恒等式:
log ( p ( x ) 2 m ( x ) ) = log ( p ( x ) m ( x ) ) − log 2 \log \left( \frac{p(x)}{2m(x)} \right) = \log \left( \frac{p(x)}{m(x)} \right) - \log 2 log(2m(x)p(x))=log(m(x)p(x))−log2log ( a b ) = log a − log b \log \left( \frac{a}{b} \right) = \log a - \log b log(ba)=loga−logb
所以:
V ( D ∗ , G ) = K L ( p r ∥ m ) + K L ( p g ∥ m ) − 2 log 2 V(D^*, G) = KL(p_r \| m) + KL(p_g \| m) - 2 \log 2 V(D∗,G)=KL(pr∥m)+KL(pg∥m)−2log2小结:对抗损失在 D ∗ D^* D∗ 时,等价于:
V ( D ∗ , G ) = 2 ⋅ J S ( p r ∥ p g ) − 2 log 2 V(D^*, G) = 2 \cdot JS(p_r \| p_g) - 2 \log 2 V(D∗,G)=2⋅JS(pr∥pg)−2log2也就是说:GAN 实际上在最小化 JS 散度
5. 支持集不重叠时的问题
如图所示:

- 图 A:两个分布完全不重叠, J S = log 2 JS = \log 2 JS=log2;
- 图 B:两者有轻微重叠,JS 仍较大。
在这种情况下, J ( G ) J^{(G)} J(G) 的梯度为 0:
∇ θ g J ( G ) = 0 \nabla_{\theta_g} J^{(G)} = 0 ∇θgJ(G)=0
这意味着:生成器无法收到任何学习信号!
这是原始 GAN 的根本性问题所在。
图 A:无重叠的支持集
红色区域代表真实数据的概率密度 p r ( x ) p_r(x) pr(x);
黄色区域代表生成器生成的数据密度 p g ( x ) p_g(x) pg(x);
二者没有任何交集(支持集 disjoint):
supp ( p r ) ∩ supp ( p g ) = ∅ \text{supp}(p_r) \cap \text{supp}(p_g) = \varnothing supp(pr)∩supp(pg)=∅
此时最优判别器为:
D ∗ ( x ) = { 1 x ∈ supp ( p r ) 0 x ∈ supp ( p g ) D^*(x) = \begin{cases} 1 & x \in \text{supp}(p_r) \\ 0 & x \in \text{supp}(p_g) \end{cases} D∗(x)={10x∈supp(pr)x∈supp(pg)
- 对于 K L ( p ∣ m ) KL(p | m) KL(p∣m):
仅在 p ( x ) > 0 p(x) > 0 p(x)>0 的地方有贡献,此时 m ( x ) = 1 2 p ( x ) m(x) = \frac{1}{2}p(x) m(x)=21p(x),所以:
K L ( p ∥ m ) = ∑ x ∈ supp ( p ) p ( x ) log ( p ( x ) 1 2 p ( x ) ) = ∑ x ∈ supp ( p ) p ( x ) log 2 = log 2 KL(p \| m) = \sum_{x \in \text{supp}(p)} p(x) \log \left( \frac{p(x)}{\frac{1}{2}p(x)} \right) = \sum_{x \in \text{supp}(p)} p(x) \log 2 = \log 2 KL(p∥m)=∑x∈supp(p)p(x)log(21p(x)p(x))=∑x∈supp(p)p(x)log2=log2
因为 ∑ x ∈ supp ( p ) p ( x ) = 1 \sum_{x \in \text{supp}(p)} p(x) = 1 ∑x∈supp(p)p(x)=1。
导致 V ( D ∗ , G ) = 2 ⋅ log 1 2 = − 2 log 2 V(D^*, G) = 2 \cdot \log \frac{1}{2} = -2 \log 2 V(D∗,G)=2⋅log21=−2log2,即:
J S ( p r ∥ p g ) = log 2 JS(p_r \| p_g) = \log 2 JS(pr∥pg)=log2因为 JS 散度已达最大值,其导数(梯度)为 0,生成器 无法获得有效梯度,这就是梯度消失问题的本质。
图 B:轻微重叠的支持集
真实分布和生成分布有部分重叠:
supp ( p r ) ∩ supp ( p g ) ≠ ∅ \text{supp}(p_r) \cap \text{supp}(p_g) \neq \varnothing supp(pr)∩supp(pg)=∅
在重叠区域中, D ∗ ( x ) D^*(x) D∗(x) 不再是 0 或 1,而是一个概率:
D ∗ ( x ) = p r ( x ) p r ( x ) + p g ( x ) ∈ ( 0 , 1 ) D^*(x) = \frac{p_r(x)}{p_r(x) + p_g(x)} \in (0,1) D∗(x)=pr(x)+pg(x)pr(x)∈(0,1)
因此:
J S ( p r ∥ p g ) < log 2 JS(p_r \| p_g) < \log 2 JS(pr∥pg)<log2
梯度 ∇ θ g J ( G ) \nabla_{\theta_g} J^{(G)} ∇θgJ(G) 不再为零,生成器可以继续更新。
公式结合解释
从前面的推导我们知道:
V ( D ∗ , G ) = 2 ⋅ J S ( p r ∥ p g ) − 2 log 2 V(D^*, G) = 2 \cdot JS(p_r \| p_g) - 2 \log 2 V(D∗,G)=2⋅JS(pr∥pg)−2log2
- 图 A: J S ( p r ∥ p g ) = log 2 ⇒ V = − 2 log 2 JS(p_r \| p_g) = \log 2 \Rightarrow V = -2 \log 2 JS(pr∥pg)=log2⇒V=−2log2,梯度消失;
- 图 B: J S ( p r ∥ p g ) < log 2 ⇒ V > − 2 log 2 JS(p_r \| p_g) < \log 2 \Rightarrow V > -2 \log 2 JS(pr∥pg)<log2⇒V>−2log2,仍有学习信号。
Wasserstein GAN :从距离度量到训练对抗目标的革新
什么是分布距离?
为度量两个概率分布 P P P 和 Q Q Q 的差异,常见方法包括:
KL 散度(Kullback–Leibler divergence):
K L ( P ∥ Q ) = ∑ x P ( x ) log ( P ( x ) Q ( x ) ) KL(P \| Q) = \sum_x P(x) \log \left( \frac{P(x)}{Q(x)} \right) KL(P∥Q)=x∑P(x)log(Q(x)P(x))JS 散度(Jensen–Shannon divergence):
J S ( P ∥ Q ) = 1 2 K L ( P ∥ P + Q 2 ) + 1 2 K L ( Q ∥ P + Q 2 ) JS(P \| Q) = \frac{1}{2} KL\left(P \| \frac{P+Q}{2} \right) + \frac{1}{2} KL\left(Q \| \frac{P+Q}{2} \right) JS(P∥Q)=21KL(P∥2P+Q)+21KL(Q∥2P+Q)Wasserstein 距离(Earth-Mover Distance):
W ( P ∥ Q ) = inf γ ∈ Π ( P , Q ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W(P \| Q) = \inf_{\gamma \in \Pi(P, Q)} \mathbb{E}_{(x, y) \sim \gamma}[\|x - y\|] W(P∥Q)=γ∈Π(P,Q)infE(x,y)∼γ[∥x−y∥]
其中 γ \gamma γ 是所有边缘分布分别为 P P P 和 Q Q Q 的联合分布集合 Π ( P , Q ) \Pi(P, Q) Π(P,Q)。可理解为:将 P P P 的质量“搬运”到 Q Q Q 所需的最小代价。
KL / JS / W 三种距离的对比示意
我们来考虑一个简单案例: P 1 P_1 P1 和 P 2 P_2 P2 是两个具有间隔 θ \theta θ 的分布。
| 距离类型 | 数学形式 | 特性 |
|---|---|---|
| K L ( P 1 ∣ P 2 ) KL(P_1 | P_2) KL(P1∣P2) | ∞ \infty ∞(若 θ ≠ 0 \theta \ne 0 θ=0);0(若 θ = 0 \theta = 0 θ=0) | 不连续;无梯度 |
| J S ( P 1 ∣ P 2 ) JS(P_1 | P_2) JS(P1∣P2) | log 2 \log 2 log2(若 θ ≠ 0 \theta \ne 0 θ=0);0(若 θ = 0 \theta = 0 θ=0) | 不连续;梯度为零 |
| W ( P 1 , P 2 ) W(P_1, P_2) W(P1,P2) | $ | \theta |
结论:Wasserstein 距离对分布支持集是否重叠不敏感,始终提供有用的梯度。
Wasserstein GAN 正式引入
WGAN 引入 Earth-Mover 距离作为衡量真实分布 P r P_r Pr 和生成分布 P g P_g Pg 的距离:
W ( P r , P g ) = inf γ ∈ Π ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r, P_g)} \mathbb{E}_{(x, y) \sim \gamma}[\|x - y\|] W(Pr,Pg)=γ∈Π(Pr,Pg)infE(x,y)∼γ[∥x−y∥]
但由于直接优化该形式极其困难,WGAN 利用其对偶形式重写:
W ( P r , P g ) = sup ∥ f ∥ L ≤ 1 E x ∼ P r [ f ( x ) ] − E x ∼ P g [ f ( x ) ] W(P_r, P_g) = \sup_{\|f\|_L \le 1} \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{x \sim P_g}[f(x)] W(Pr,Pg)=∥f∥L≤1supEx∼Pr[f(x)]−Ex∼Pg[f(x)]
这里:
f f f 是一类满足 Lipschitz 条件的函数;
∥ f ∥ L ≤ 1 \|f\|_L \le 1 ∥f∥L≤1 表示 f f f 是 1-Lipschitz 连续函数;
∣ ∣ f ( x ) − f ( y ) ∣ ∣ ≤ ∥ x − y ∥ ||f(x) - f(y)|| \le \|x - y\| ∣∣f(x)−f(y)∣∣≤∥x−y∥
“supremum” 表示在所有满足条件的函数中取最大值。
对于更一般的 K-Lipschitz 函数( ∣ ∣ f ∣ ∣ L ≤ K ||f||_L \le K ∣∣f∣∣L≤K),有:
W ( P r , P g ) = 1 K sup ∥ f ∥ L ≤ K E x ∼ P r [ f ( x ) ] − E x ∼ P g [ f ( x ) ] W(P_r, P_g) = \frac{1}{K} \sup_{\|f\|_L \le K} \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{x \sim P_g}[f(x)] W(Pr,Pg)=K1∥f∥L≤KsupEx∼Pr[f(x)]−Ex∼Pg[f(x)]
什么是 K-Lipschitz 函数?
函数 f f f 是 K-Lipschitz 的含义为:
∥ f ( x ) − f ( y ) ∥ ≤ K ⋅ ∥ x − y ∥ 对所有 x , y 成立 \|f(x) - f(y)\| \le K \cdot \|x - y\| \quad \text{对所有 } x, y \text{ 成立} ∥f(x)−f(y)∥≤K⋅∥x−y∥对所有 x,y 成立
- 当 K = 1 K = 1 K=1,即为标准的 1-Lipschitz 函数;
- Lipschitz 条件确保 f f f 的梯度幅度不会过大,提供优化稳定性。
这个约束是 WGAN 成立的理论基础,也是后续训练中判别器(critic)要满足的重要条件。
用神经网络近似 Lipschitz 函数
为近似 Lipschitz 函数族 { f } \{f\} {f},WGAN 引入判别器(或称 critic) f w f_w fw,令其参数 w w w 落在某个约束空间中(如 w ∈ [ − c , c ] w \in [-c, c] w∈[−c,c]),以保证 f w f_w fw 是 Lipschitz。
最终形式为:
W ( P r , P g ) ≈ max w ∈ W E x ∼ P r [ f w ( x ) ] − E x ∼ P g [ f w ( x ) ] W(P_r, P_g) \approx \max_{w \in \mathcal{W}} \mathbb{E}_{x \sim P_r}[f_w(x)] - \mathbb{E}_{x \sim P_g}[f_w(x)] W(Pr,Pg)≈w∈WmaxEx∼Pr[fw(x)]−Ex∼Pg[fw(x)]
其中 W \mathcal{W} W 是所有 K K K-Lipschitz 参数的集合。
WGAN 做法:使用 weight clipping 强制 f w f_w fw 满足 Lipschitz 条件。
例如: W = [ − c , c ] l W =[−c, c]^l W=[−c,c]l为了满足这一要求,WGAN通过应用权值裁剪(weight clipping)来强制D在紧化空间[-c, c]中的权值
WGAN 的训练目标
判别器(Critic)优化目标:
L D = E x ∼ P r [ f w ( x ) ] − E x ∼ P g [ f w ( x ) ] \mathcal{L}_D = \mathbb{E}_{x \sim P_r}[f_w(x)] - \mathbb{E}_{x \sim P_g}[f_w(x)] LD=Ex∼Pr[fw(x)]−Ex∼Pg[fw(x)]
即最大化 Wasserstein 距离。
生成器优化目标:
L G = − E x ∼ P g [ f w ( x ) ] = − E z ∼ p ( z ) [ f w ( G ( z ) ) ] \mathcal{L}_G = -\mathbb{E}_{x \sim P_g}[f_w(x)] = -\mathbb{E}_{z \sim p(z)}[f_w(G(z))] LG=−Ex∼Pg[fw(x)]=−Ez∼p(z)[fw(G(z))]
即最小化 Wasserstein 距离。
WGAN 相比传统 GAN 的优势
| 指标 | 原始 GAN | WGAN |
|---|---|---|
| 判别器输出 | 概率(0~1) | 实值(任意实数) |
| 判别器损失 | JS 散度 | Wasserstein 距离 |
| 训练稳定性 | 极差,易崩 | 稳定,可控 |
| 梯度消失 | 常见 | 极少 |
WGAN 本质上是将原始 GAN 中的 JS 散度替换为 Wasserstein 距离,从而有效解决了梯度消失与训练不稳定的问题。
WGAN 训练算法流程
超参数设定
- α \alpha α:学习率(建议 5 × 10 − 5 5 \times 10^{-5} 5×10−5)
- c c c:权重裁剪边界(如 ± 0.01 \pm 0.01 ±0.01)
- m m m:每个批次的数据量(如 64)
- n critic n_{\text{critic}} ncritic:每次更新生成器前,critic 网络的更新次数(通常为 5)
整体流程
初始化参数:critic 的参数 w 0 w_0 w0,生成器参数 θ 0 \theta_0 θ0。
迭代训练:直到 θ \theta θ 收敛:
Step 1:更新 critic(判别器) n critic n_{\text{critic}} ncritic 次:
从真实数据分布 P r P_r Pr 中采样一个 minibatch { x ( i ) } \{x^{(i)}\} {x(i)};
从潜在分布 p ( z ) p(z) p(z) 中采样一组噪声 { z ( i ) } \{z^{(i)}\} {z(i)};
计算损失的梯度:
g w ← ∇ w [ 1 m ∑ i = 1 m f w ( x ( i ) ) − f w ( g θ ( z ( i ) ) ) ] g_w \leftarrow \nabla_w \left[ \frac{1}{m} \sum_{i=1}^m f_w(x^{(i)}) - f_w(g_\theta(z^{(i)})) \right] gw←∇w[m1i=1∑mfw(x(i))−fw(gθ(z(i)))]用 RMSProp 或 SGD 执行梯度上升:
w ← w + α ⋅ RMSProp ( w , g w ) w \leftarrow w + \alpha \cdot \text{RMSProp}(w, g_w) w←w+α⋅RMSProp(w,gw)执行 weight clipping:
w ← clip ( w , − c , c ) w \leftarrow \text{clip}(w, -c, c) w←clip(w,−c,c)
这一步保证 f w f_w fw 是 K-Lipschitz 函数(保持对偶形式成立)。
Step 2:更新生成器 G θ G_\theta Gθ 一次:
从噪声分布 p ( z ) p(z) p(z) 中采样 z ( i ) z^{(i)} z(i);
计算生成器梯度(负 critic 输出):
g θ ← − ∇ θ [ 1 m ∑ i = 1 m f w ( g θ ( z ( i ) ) ) ] g_\theta \leftarrow -\nabla_\theta \left[ \frac{1}{m} \sum_{i=1}^m f_w(g_\theta(z^{(i)})) \right] gθ←−∇θ[m1i=1∑mfw(gθ(z(i)))]执行梯度下降:
θ ← θ − α ⋅ RMSProp ( θ , g θ ) \theta \leftarrow \theta - \alpha \cdot \text{RMSProp}(\theta, g_\theta) θ←θ−α⋅RMSProp(θ,gθ)
有意义的损失指标(Meaningful Loss Metric)
GAN 的一个关键问题是:损失值是否能有效反映生成样本的质量?
Vanilla GAN 的问题
如下图所示,Vanilla GAN 使用 JS 散度(JSD estimate)作为训练目标,但其在训练过程中的表现不稳定且无法作为样本质量的衡量指标:
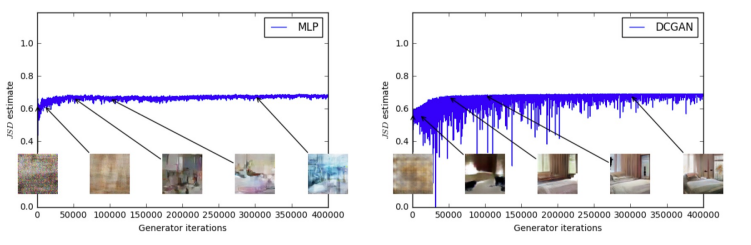
- 左图:MLP 生成器在训练过程中,生成样本逐渐变好,但 JSD 并没有显著下降。
- 右图:DCGAN 生成器样本质量明显提升,但 JSD 曲线波动剧烈,甚至略有上升。
结论:JSD 损失和样本质量之间没有明显的正相关性,因此 JSD 并不是一个有意义的训练指标。
WGAN 的优势
相比之下,WGAN 使用 Wasserstein 距离作为训练目标,其数值变化与生成样本的质量变化高度一致:

- 左图:MLP 生成器从模糊块逐渐生成清晰卧室图像,Wasserstein 距离稳定下降;
- 右图:DCGAN 同样表现出 Wasserstein 距离逐步收敛,与图像质量一致。
结论:WGAN 的损失函数具有实际意义,能够真实反映训练进度与样本质量。