混合效应模型(Mixed Effects Model)
对于数据来说,我们通常把所有样本共有的影响因素(性别,实验处理,实验方法),这种可以推广到总体的叫做固有效应,而仅适用于特定分组的(个体差异),叫做随机效应,混合效应模型就是用于处理既有固有效应又有随机效应的方法。
举一些具体点的例子,像同一个患者在一周内的血压数据,不同班级的学生成绩,不同地区的空气质量和查看对照实验的结果等,我们可以看到这些数据都有一些共同的特点,数据基本都有分组,且每个分组内的数据都有自己的特点,像学生成绩的固有效应就来自于考试的卷子难度,而随机效应既有学生的个体差异,也有师资差异,这需要我们在使用的时候有自己的判断。
下面我们举一个学生成绩的例子来举例:
set.seed(123)
n_students <- 100
n_classes <- 5
# 模拟数据(保持不变)
data <- data.frame(
student_id = 1:n_students,
class_id = sample(1:n_classes, n_students, replace = TRUE),
teaching_method = sample(c("A", "B"), n_students, replace = TRUE),
baseline_score = rnorm(n_students, mean = 70, sd = 10)
)
data$score <- with(data,
baseline_score +
ifelse(teaching_method == "A", 5, -2) + # 固定效应
rnorm(n_classes, sd = 3)[class_id] + # 随机效应(班级)
rnorm(n_students, sd = 2) # 个体误差
)
# 拟合模型(添加错误处理)
tryCatch({
model <- lmer(score ~ teaching_method + (1 | class_id), data = data)
summary(model)
}, error = function(e) {
message("lme4出错,改用nlme包:")
library(nlme)
model <- lme(score ~ teaching_method, random = ~ 1 | class_id, data = data)
summary(model)
})
# 绘图(保持不变)
ggplot(data, aes(x = teaching_method, y = score, color = factor(class_id))) +
geom_boxplot() +
labs(title = "成绩按教学方法和班级分布",
x = "教学方法",
color = "班级") +
theme_minimal()输出:
Random effects:
Formula: ~1 | class_id
(Intercept) Residual
StdDev: 1.056784 11.59231
Fixed effects: score ~ teaching_method
Value Std.Error DF t-value p-value
(Intercept) 75.44703 1.692050 94 44.58913 0e+00
teaching_methodB -7.93749 2.323873 94 -3.41563 9e-04
从输出可以看得出来,班级间的差异只有1.06,说明班级的分类对成绩的影响较小,而同一班级内不同学生的差异来到了11.59,说明成绩的变化主要来自于学生自己(比如有课外补习,下课有的人会勤快的问老师问题,有的学生特别聪明等);而从教学方法的p值可以看出,A教学方法对成绩的提升是最明显的,如果是研究不同老师的教学能力,可以将其纳入指标中(前提是控制学生群体相同),注意如果班级的数量大于5,即使随机效应里的标准差较小,最好也采用混合模型,因为班级数量太多的话,班级数量会呈现一定的结构,采用不同的模型可能会忽略层级结构的影响。
生存分析(Survival Analysis)
生存分析,很容易联想到是预测病人死亡的案例,事实上,确实是这样,生存分析是用来预测某个事件发生前的时间,像病人从治疗到死亡的时间,机器从使用到故障的时间,用户从注册到流失的时间等,反映出的核心问题是,在某个时间点,事件发生的概率是多少。
生存分析的关键在于从开始观察到事件发生的时间段内,是否发生了我们想要看到的事件,像预测病人死亡时,我们就会用到生存分析,但不一样的是,我们需要对数据进行筛选,就像生存分析的核心所说的,要筛选出符合所要事件的数据,当然了,这就跟指标有关了,比如在医学中常见的课题:患某类病的病人,在患有另一种病后死亡的概率,这种就需要筛选病人的药物,两种病的合并症,拿取的数据是否是在两类病发生中间的等等。而且,生存分析还可以利用缺少”结局“的数据,即如果病人还活着的数据,而不需要人为地赋予一个结局。
总而言之,通过生存分析,我们可以关注到是哪些因素影响到了事件发生的概率。
依然是通过一个例子来说明:
set.seed(123)
n <- 100
treatment <- sample(c("A", "B"), n, replace = TRUE)
data <- data.frame(
patient_id = 1:n,
treatment = treatment,
age = rnorm(n, mean = 60, sd = 10),
time_to_event = round(rexp(n, rate = ifelse(treatment == "A", 0.01, 0.02)) + 30),
event = rbinom(n, 1, 0.8)
)
# 生存分析
surv_obj <- Surv(data$time_to_event, data$event)
fit <- survfit(surv_obj ~ treatment, data = data)
# 绘制生存曲线
ggsurvplot(fit, data = data,
pval = TRUE, # 显示组间差异p值
risk.table = TRUE, # 显示风险表
title = "生存曲线(治疗A vs B)")
# Cox模型(分析影响因素)
cox_model <- coxph(Surv(time_to_event, event) ~ treatment + age, data = data)
summary(cox_model)输出:
Call:
coxph(formula = Surv(time_to_event, event) ~ treatment + age,
data = data)
n= 100, number of events= 75
coef exp(coef) se(coef) z Pr(>|z|)
treatmentB 1.012157 2.751528 0.266035 3.805 0.000142 ***
age -0.007869 0.992162 0.012148 -0.648 0.517146
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
treatmentB 2.7515 0.3634 1.6335 4.635
age 0.9922 1.0079 0.9688 1.016
Concordance= 0.626 (se = 0.036 )
Likelihood ratio test= 14.09 on 2 df, p=9e-04
Wald test = 14.57 on 2 df, p=7e-04
Score (logrank) test = 15.58 on 2 df, p=4e-04
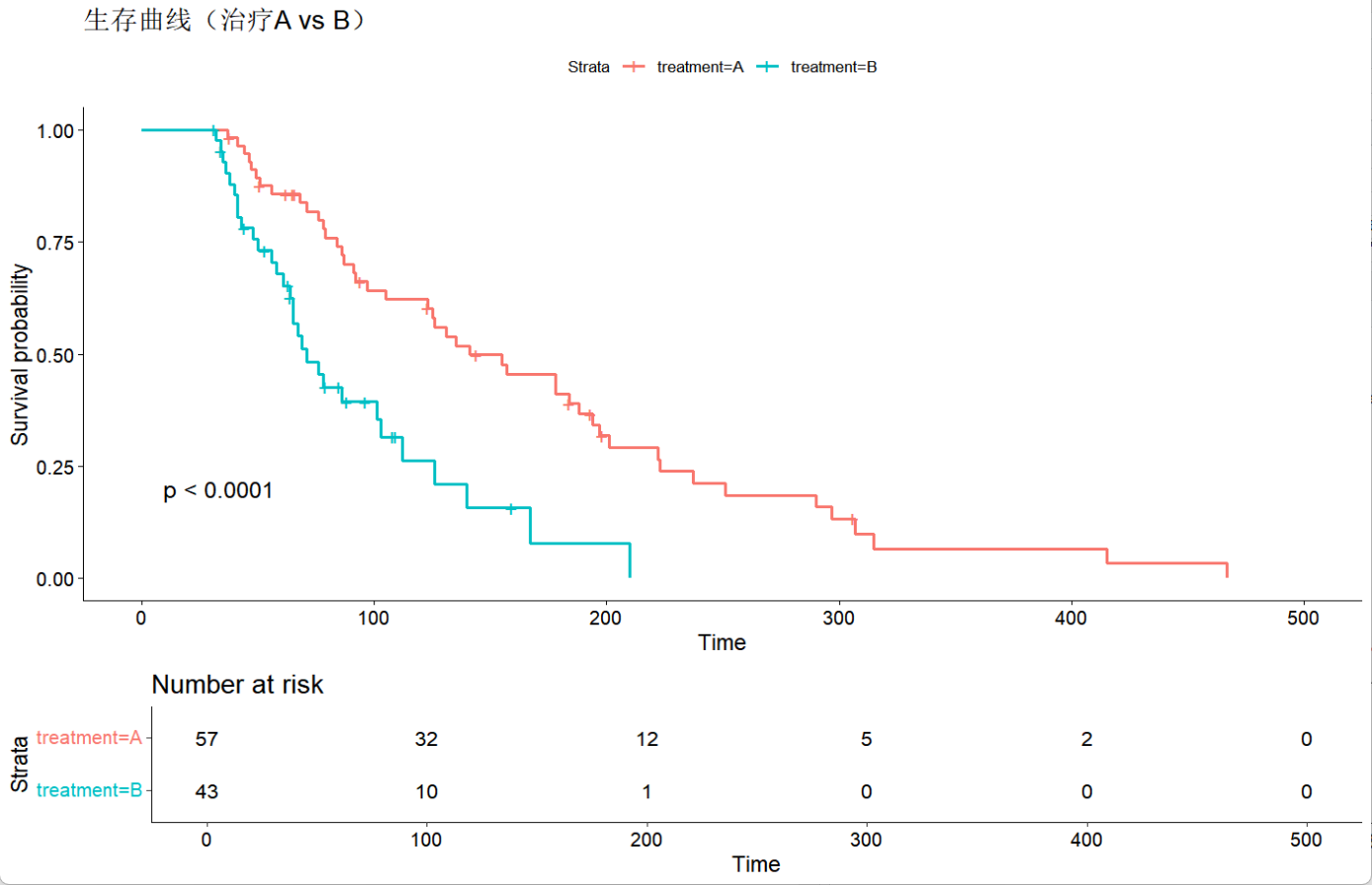
从输出我们可以看到,在100个样本数据中,有缺失数据的有25个。而通过观察年龄和治疗方案的输出,首先从三个检验值Likelihood ratio test,Wald test和Score test能看出模型整体是存在差异的,说明至少有一个预测变量起到了显著影响,而通过观察coef和p值,我们可以判断年龄对病人的生存时间没有太大影响,相反治疗方案的选择,在死亡风险上展示出了较大的差异。不过模型的C-index为0.626,接近于0.5,说明模型的解释力一般,要谨慎对待结果。