Double/Debiased Machine Learning

独立同步分布的观测数据 { W i = ( Y i , D i , X i ) ∣ i ∈ { 1 , . . . , n } } \{W_i=(Y_i,D_i,X_i)| i\in \{1,...,n\}\} {Wi​=(Yi​,Di​,Xi​)∣i∈{1,...,n}}，其中$Y_i$表示结果变量，$D_i$表示因变量，$X_i$表示控制变量。

目标参数${\theta }_0$的一般定义形式为：

$$E[m(W;{\theta }_0,{\eta }_0)]=0$$

$W$为观测到的变量，${\theta }_0\in \Theta$为目标参数，${\eta }_0\in \mathcal{T}$为辅助参数

例如，ATE 的定义为：

$${\theta }_0^{ATE}\equiv E[E[Y_i|D_i=1,X_i]-E[Y_i|D_i=0,X_i]]$$

ATE的IPW估计定义为：

$$m_{IPW}(W_i;\theta ,\alpha )\equiv \alpha (D_i,X_i)Y_i-\theta \equiv [\frac{D_i}{E[D_i|X_i]}-\frac{1-D_i}{1-E[D_i|X_i]}]Y_i-\theta$$

ATE的Doubly Robust估计的定义为：

$$m_{DR}(W_i;\theta ,\eta )\equiv \alpha (D_i,X_i)(Y_i-E[Y_i|D_i,X_i])Y_i+E[Y_i|D_i=1,X_i]-E[Y_i|D_i=0,X_i]-\theta$$

$$\equiv [\frac{D_i}{E[D_i|X_i]}-\frac{1-D_i}{1-E[D_i|X_i]}]Y_i+E[Y_i|D_i=1,X_i]-E[Y_i|D_i=0,X_i]-\theta$$

一般情况下，目标参数${\theta }_0$的估计值定义为：

$$\hat{\theta }:\frac{1}{n}\sum _{i=1}^{n}m(W_i;\hat{\theta },\hat{\eta })=0$$

一阶泰勒展得出：

$$\frac{1}{n}\sum _{i=1}^{n}m(W_i;\hat{\theta },\hat{\eta })\approx \frac{1}{n}\sum _{i=1}^{n}m(W_i;{\theta }_0,{\eta }_0)+\frac{1}{n}\sum _{i=1}^n\frac{\partial }{\partial \theta }m(W_i;{\theta }_0,{\eta }_0)(\hat{\theta }-{\theta }_0)+\frac{1}{n}\sum _{i=1}^n\frac{\partial }{\partial \eta }m(W_i;{\theta }_0,{\eta }_0)(\hat{\eta }-{\eta }_0)\approx 0$$

$$({\theta }_0-\hat{\theta })\approx [\frac{1}{n}\sum _{i=1}^n\frac{\partial }{\partial \theta }m(W_i;{\theta }_0,{\eta }_0){]}^{-1}\frac{1}{n}\sum _{i=1}^{n}m(W_i;{\theta }_0,{\eta }_0)+[\frac{1}{n}\sum _{i=1}^n\frac{\partial }{\partial \theta }m(W_i;{\theta }_0,{\eta }_0){]}^{-1}(\hat{\eta }-{\eta }_0)\frac{1}{n}\sum _{i=1}^n\frac{\partial }{\partial \eta }m(W_i;{\theta }_0,{\eta }_0)$$

目标参数的估计偏差$({\theta }_0-\hat{\theta })$将受到辅助参数估计偏差$(\hat{\eta }-{\eta }_0)$的影响，说明目标参数的估计偏差的两种来源分别是：

• 辅助参数的估计偏差$(\hat{\eta }-{\eta }_0)$本身，称之为正则化偏差
• 辅助参数的估计偏差$(\hat{\eta }-{\eta }_0)$与$W_i$的强相关性，称之为过拟合偏差

Neyman Orthogonality

∂ ∂ λ { E [ ψ ( W i ; θ 0 , η 0 + λ ( η − η 0 ) ) ] } ∣ λ = 0 = 0 , ∀ η ∈ T \frac{\partial}{\partial\lambda}\{E[\psi(W_i;\theta_0,\eta_0 + \lambda(\eta-\eta_0))]\}|_{\lambda=0}= 0,\forall\eta\in \mathcal{T} ∂λ∂​{E[ψ(Wi​;θ0​,η0​+λ(η−η0​))]}∣λ=0​=0,∀η∈T

$m_{IPW}$ is not Neyman orthogonal, $m_{DR}$ is Neyman orthogonal.

Cross Fitting

$$\hat{\theta }:\frac{1}{n}\sum _{k=1}^K\sum _{i\in I_k}m(W_i;\hat{\theta },{\hat{\eta }}_{-k})=0$$

DML

$$\hat{\theta }:\frac{1}{n}\sum _{k=1}^K\sum _{i\in I_k}\psi (W_i;\hat{\theta },{\hat{\eta }}_{-k})=0$$

直接回归不满足 Neyman 正交性

$$Y=\theta T+g(X)+ϵ$$

$$m(W;\theta ,g)=Y-\theta T-g(X)+ϵ$$

$$\frac{\partial }{\partial \lambda }E[m(w;\theta ,g+\lambda \Delta g)]{|}_{\lambda =0}=E[-\Delta g(x)]\ne 0$$

DML 满足Neyman正交性

$$Y-l(x)=\theta (T-m(x))+{ϵ}^{\prime },l(x)=E[Y|X=x],m(x)=E[T|X=x]$$

$$m(W;\theta ,\eta )=Y-l(x)-\theta (T-m(x))-{ϵ}^{\prime },\eta =(l,m)$$

$$\frac{\partial }{\partial \lambda }E[W;\theta ,\eta +\lambda \Delta \eta ]{|}_{\lambda =0}=E[-\Delta l(x)+\theta \Delta m(x)]=0$$

Example

模拟数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
import dowhy.datasets, dowhy.plotter
rvar = 1 if np.random.uniform() > 0.2 else 0
is_linear = False # A non-linear dataset. Change to True to see results for a linear dataset.
data_dict = dowhy.datasets.xy_dataset(10000, effect=rvar,
                                      num_common_causes=2,
                                      is_linear=is_linear,
                                      sd_error=0.2)
df = data_dict['df']
print(df.head())
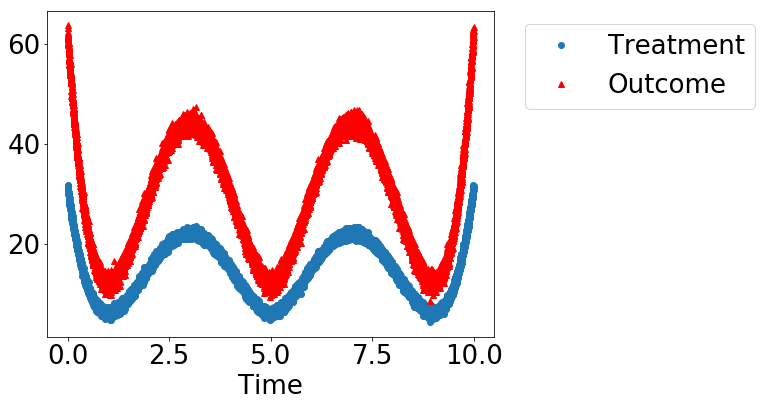
dowhy.plotter.plot_treatment_outcome(df[data_dict["treatment_name"]], df[data_dict["outcome_name"]],
                             df[data_dict["time_val"]])

因果关系假设：

• 基于领域知识提出因果关系的假设，定义模型结构

from dowhy import CausalModel
model= CausalModel(
        data=df,
        treatment=data_dict["treatment_name"],
        outcome=data_dict["outcome_name"],
        common_causes=data_dict["common_causes_names"],
        instruments=data_dict["instrument_names"])
model.view_model(layout="dot")

因果关系识别：

identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)

因果关系估计：

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LassoCV
from sklearn.ensemble import GradientBoostingRegressor
dml_estimate = model.estimate_effect(identified_estimand, method_name="backdoor.econml.dml.DML",
                                     control_value = 0,
                                     treatment_value = 1,
                                 confidence_intervals=False,
                                method_params={"init_params":{'model_y':GradientBoostingRegressor(),
                                                              'model_t': GradientBoostingRegressor(),
                                                              "model_final":LassoCV(fit_intercept=False),
                                                              'featurizer':PolynomialFeatures(degree=2, include_bias=True)},
                                               "fit_params":{}})
print(dml_estimate)

因果关系反驳测试：

res_placebo=model.refute_estimate(identified_estimand, dml_estimate,
        method_name="placebo_treatment_refuter", placebo_type="permute",
        num_simulations=20)
print(res_placebo)