一、单值二叉树
二叉树为二叉链表形式，结点为：
大概看看题就知道这道题让我们判断一个树到底所有结点的值是不是相同，相同就是单值二叉树。在实现二叉树相关操作的时候已经体会到了，递归来遍历二叉树是非常舒服的（做这些题本质都得遍历）。
所以我们考虑考虑递归怎么个递归法，而二叉树递归其实就是考虑根结点以及左右子树之间的关系。
容易想到判断根结点与左右孩子结点是否结点，当然，由于需要访问左右孩子结点，根结点不能为空，而且因为访问的是三个结点的值，所以肯定三个结点都得先保证不为空。
这个就有点讲究了，根结点不能为空，假设刚好遍历到一个空结点，空结点的值实际上并不是二叉树实际上的值，对二叉树是不是单值二叉树不影响，所以碰见为空返回值需要不影响判断结果。
接下来就是分别判断左右子树是不是也符合了，这个逻辑就简单了，因为直接上递归就行，新的根结点分别是root->left和root->right，其它就没了。
代码表达：
只不过最后的递归直接省成一个布尔表达式了，因为能走到最后一个retrun语句至少说明根结点和它的左右孩子符合单值二叉树，如果左右子树同时符合单值二叉树，那肯定就是单值二叉树，但凡出现不符合的情况，我们给出来的语句都可以判断，且有&&，一个不符合最后都是false。
测试通过：
提交通过：
二、相同的树
给你一个树，你得给我判断出来到底是相同还是不同的，什么是相同的树呢，结构和数值完全一样的树就是相同的树。比如典例2，典型的数值一样，但是同样的根结点，左边的树，左孩子为2，右孩子为空；典例3这俩树不看数值其实是完全一样的，但是孩子结点的数值并不是一一对应的。
其实说来还是遍历，只不过是同步遍历，也就是这样：
如果同步遍历完了还没有检测出不一样的结点，显然就是相同的树，否则就是不同的树。
还是立足根结点写出代码，再用递归去判断左右子树的情况。
因为要判断值，所以肯定保证根不为空，因为两个根，所以就有三种情况了：
都为空，一个为空（显然不是相同树，因为同步遍历），都不为空。
只不过需要注意的是第二个条件的写法，全空已经排除过了，那至少有一个为非空，此时就剩下一个空一个非空和全非空，如果再有空岂不是就是一个空一个非空了嘛，直接return false就行，其它都简单。
三、对称二叉树
这道题其实基本不用做了，因为如果相同二叉树做出来了，那么对称二叉树很明显就是每次遍历的结点刚好走的路径相反而已：
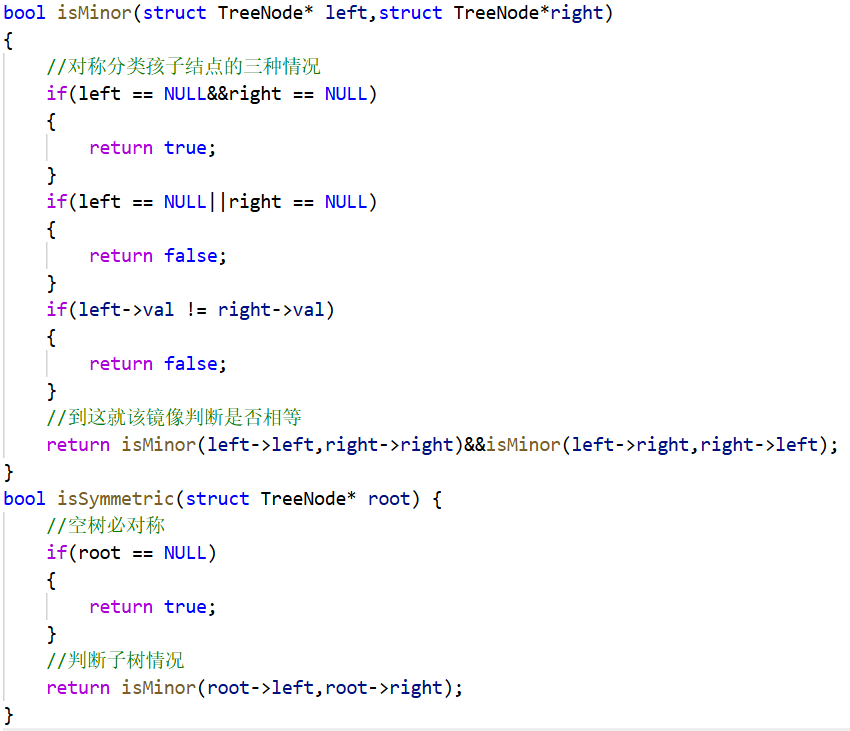
分类基本是模仿相同树来的，当然，return啥肯定得对着典例写。
比较容易弄错的就是最后递归按镜像走路，不过对着典例写就行。
四、另一棵树的子树
其实这个题在我们做过判断二叉树是否相同以后就简单了，遍历整棵树，如果找到和subRoot相同根结点的结点的值，这里就可能是子树可能相同的地点，直接套判断相同的树的代码就可以了。
root防止为空是考虑到了在遍历的过程中可能一条路走到黑而导致触发空结点，return false是作为递归的终点，代表这条路找不到能与subRoot这个根结点相同的值。
如果找到了，就判断是否相同，不相同就一直遍历，直到遍历完整个树。
但是代码一碰见这蔫了，因为找到结点相同的了，就判断是不是相同，那肯定不同啊，相当于这样：
这样能通过就怪了。
想出来个这修改真是艰难，因为判断相等是肯定要有的，那干脆别以值相等做条件了，万一前面有跟上面这个例子一样，递归还没展开，先找到相等的值，那不直接炸了，如果递归展开了，就不用老担心：
这个图就是递归已经展开了才被拦截，最后肯定还是能找到只有1的subRoot。
所以直接一点，改成有相等的树才能返回true，不然就遍历完整棵树后返回false。
五、二叉树的遍历（前中后序）
遍历的思想基本没啥可讲了，但是放在oj题里可没有那么轻轻松松就能做出来：
比如前序遍历，最难的其实不是前序遍历完二叉树，注意看最后的返回值，要的是int*类型的
但是实际上这道题的意思是最后把遍历的数据放到数组最后返回数组的地址，这个数组还必须是动态开辟的数组，并且参数returnSize是用来确定遍历到的二叉树的结点的个数（最终存到数组内的元素个数）给远程服务器，前序遍历简单，但是一个一个放这些数据就有点讲究了。
上来问题就来了，那就是开辟多大空间的数组，那就免不了遍历二叉树去计算二叉树结点个数：
准备好以后就该前序遍历，并放到数组里：
最重要的就是写出来怎么把现在遍历到的根结点放到数组里，毕竟左子树右子树的遍历仅仅是递归而已。
容易想到的是必须带上偏移量，因为每次放置一个元素以后指针肯定要后移：
偏移量肯定不能传形参，你在Dispose这个函数里面往这次的arr+i所指向的位置存了以后就该++了，但是如果传值根本不能对偏移量i产生影响。
具体细节：
必须以i的地址为一个变量一直传给preOrder函数，因为每次递归如果不传i的地址，或者传值，前者得到的结果就是每次进入新的递归以后都会新建一个int i = 0；这样会造成偏移量实际没有后移，因为每次进新函数栈帧都是重新定义i；后者传值不会对偏移量产生影响，这个见过了。
成功通过，经过这道题掌握一种“常驻变量的改变”。
至于中序后序不多bb，调换个位置而已。
六、二叉树的构建和遍历
1.先序遍历字符串构建二叉树
2.二叉树中序遍历并输出
难的就是第一步，直接画图看看最终生成的是一棵什么样的树，并在画图过程中体会代码怎么写：
容易得到，如果碰不到空结点，肯定得一直根左右，那么就是这样的，接下来该返回到b了，因为c的根左右已经结束了：
紧接着就是遍历d的左右子树：
又碰到双空就得回头了：
再还原一下，检验正确。
最重要的递归构建树：
其实也没多高级，他说啥是啥，我们只需要注意先序遍历构建的顺序即可。
其它代码很简单，直接给出来了：
当然，这里输入确实偷懒了。