光伏功率预测 | LSTM多变量单步光伏功率预测（Matlab完整源码和数据）

光伏功率预测 | MATLAB实现基于LSTM长短期记忆神经网络的光伏功率预测

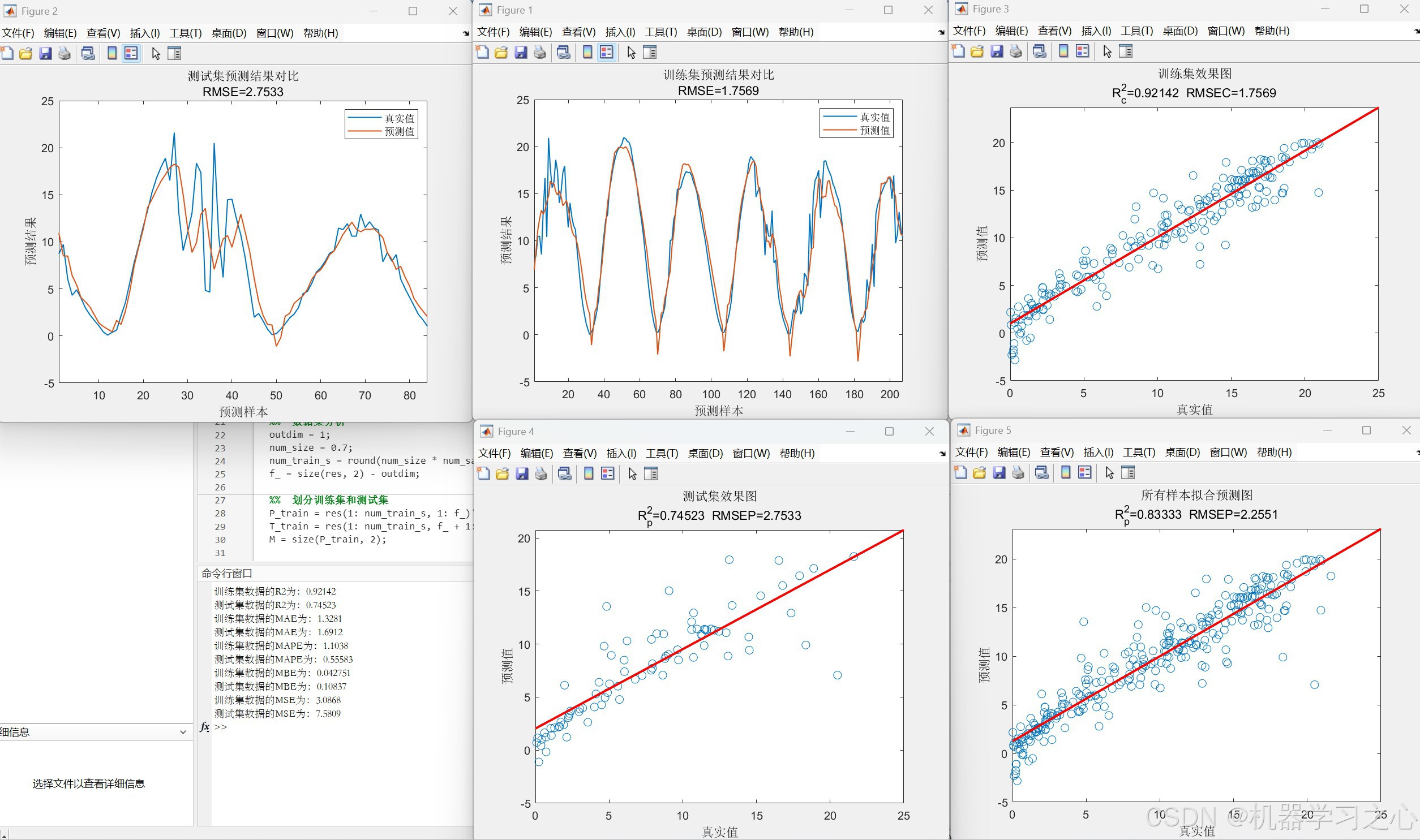
效果一览

基本介绍

光伏功率预测 | LSTM多变量单步光伏功率预测（Matlab完整源码和数据）

LSTM（长短期记忆网络）由Hochreiter和Schmidhuber于1997年提出，旨在解决传统RNN存在的长期依赖问题。其核心结构包括 细胞状态（Cell State） 和三个门控机制：

1. 遗忘门（Forget Gate） ：决定细胞状态中哪些信息需要被丢弃，通过Sigmoid函数输出0-1的权重。
   
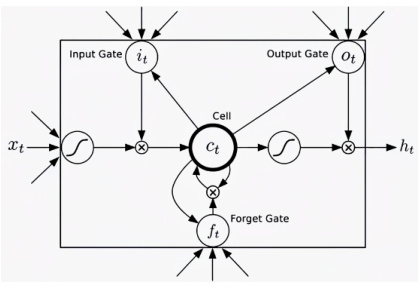
2. 输入门（Input Gate） ：筛选当前输入（如气象数据、历史功率）中需要保留的信息，并更新细胞状态。
3. 输出门（Output Gate） ：控制细胞状态对当前时刻隐藏状态$h_t$的输出，影响最终预测结果。

优势：通过门控机制和细胞状态的恒定误差流，LSTM能有效捕捉时间序列中的长期依赖关系，尤其适合光伏功率这类受历史气象条件影响显著的任务。

单步预测的适用场景与技术特点

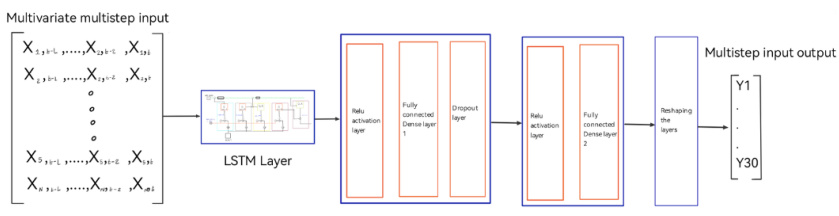
1. 定义：单步预测指利用历史数据$t-k$至$t$的输入（如气象变量、历史功率），预测$t+1$时刻的输出功率。
2. 与多步预测对比：
   • 误差累积：单步预测每次使用真实值输入，避免多步预测中误差迭代传播的问题。
   • 适用性：适合短期调度（如日内电力平衡）、实时性要求高的场景。
3. LSTM单步预测流程：
   • 输入维度：$[batch\_size,time\_steps,features]$，例如滑动窗口长度为24小时、包含5个气象变量。
   • 输出层：单神经元全连接层，直接输出下一时刻功率值。
     

评估指标与模型验证

1. 常用指标：

   • RMSE（均方根误差）：反映预测值与实际值的偏差，计算公式：
     $$\text{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n({\hat{y}}_i-y_i{)}^2}$$

   • MAE（平均绝对误差）：衡量预测误差的绝对值平均。

   • R²（决定系数）：评估模型拟合优度，接近1表示解释力强。

2. 实际应用标准：
   • 光伏功率预测允许误差范围通常为±10%（晴天）至±20%（极端天气）。
   • 在山西电力市场案例中，预测偏差均值-0.03p.u.，表明模型普遍略高估实际出力。

LSTM多变量单步预测通过整合气象时序特征与门控机制，在光伏功率预测中展现出高精度与鲁棒性。未来研究可进一步探索多模态数据融合与在线学习机制，以应对复杂气象条件下的预测挑战。

程序设计

完整代码获取链接：光伏功率预测 | LSTM多变量单步光伏功率预测（Matlab完整源码和数据）

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据
result = xlsread('北半球光伏数据.xlsx');

%%  数据分析
num_samples = length(result);  % 样本个数
or_dim = size(result, 2);      % 原始特征+输出数目
kim =  4;                      % 延时步长（kim个历史数据作为自变量）
zim =  1;                      % 跨zim个时间点进行预测

%%  划分数据集
for i = 1: num_samples - kim - zim + 1
    res(i, :) = [reshape(result(i: i + kim - 1, :), 1, kim * or_dim), result(i + kim + zim - 1, :)];
end

%%  数据集分析
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度

%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%%  数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  数据平铺
%   将数据平铺成1维数据只是一种处理方式
%   也可以平铺成2维数据，以及3维数据，需要修改对应模型结构
%   但是应该始终和输入层数据结构保持一致
P_train =  double(reshape(P_train, f_, 1, 1, M));
P_test  =  double(reshape(P_test , f_, 1, 1, N));

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718