【论文阅读33】滑坡易发性 PINN （ EG2025 )

把Newmark永久变形模型嵌入深度学习神经网络，利用物理约束提升滑坡易发性预测的空间泛化性与物理解释性，且在空间交叉验证场景下显著优于纯数据驱动模型。

期刊 Engineering Geology （2025）

作者：
Ashok Dahal（第一作者，通讯作者） , Luigi Lombardo

单位：
University of Twente, Faculty of Geo-Information Science and Earth Observation (ITC)
特文特大学 地理信息科学与地球观测学院（ITC）
荷兰 恩斯赫德，邮政信箱 217，邮编 AE 7500

[1] Dahal A, Lombardo L. Towards physics-informed neural networks for landslide prediction[J]. Engineering Geology, 2025, 344: 107852.

本研究相关补充材料可通过以下链接在线获取：
https://doi.org/10.1016/j.enggeo.2024.107852

数据可用性声明

为促进实验结果的复现性和可重复性，本文相关数据与代码已在以下GitHub仓库中公开共享：
https://github.com/ashokdahal/PINN.git

• 目前滑坡灾害易发性建模主要有两类方法：

  1. 数据驱动方法：区域尺度上表现好，但缺少物理解释性。
  2. 物理机制方法：物理一致，但计算开销大，且主要应用在局地尺度。

这两者各有优劣，缺少兼顾预测性能与物理可解释性的方法。

📊 本文方法：物理信息神经网络（PINN）

• 将Newmark永久变形模型嵌入深度神经网络，通过网络隐变量（latent variables）学习地质力学参数（如内摩擦角φ、黏聚力c/t）。
• 预测地震诱发滑坡发生概率时，不直接输出0/1，而是用以5 cm为中心的sigmoid函数，代替传统物理模型中的Heaviside阶跃函数（避免优化困难）。
• 物理方程作为损失函数中的额外约束项，与观测数据拟合项共同优化。

📈 结果与分析

• 预测性能：

  • 随机交叉验证下，PINN和纯数据驱动模型性能接近，部分区域更优。
  • 空间交叉验证下，PINN明显优于纯深度学习方法，尤其在东南部地区几乎无误判。

• 物理一致性：

  • 学到的地质力学参数空间分布合理，符合地质背景（高喜马拉雅、Siwalik山系摩擦角高，中部山区土壤区摩擦角低）。
  • **临界加速度（critical acceleration）**分布具备物理解释性，能区分高易发性区域和稳定区域。

• 模型泛化性：

  • 在数据稀缺或外推情况下，PINN具备更好的空间泛化能力。

📌 论文的意义与展望

• 意义：

  • 提供了一种结合物理机制与深度学习的方法，兼顾预测性能与物理解释性。
  • 在滑坡灾害区域性预测和准实时应用上，PINN框架具有良好前景。

• 局限性：

  • 目前仅基于永久变形模型，忽略了应力–应变全过程。
  • Ground motion数据基于经验关系，未用全波形模拟。
  • 滑坡触发过程复杂，涉及多物理过程（降雨、地震、地下水），当前模型未完全覆盖。

• 未来工作：

  • 融合应力–变形（stress–deformation）模型
  • 引入多物理过程耦合建模
  • 使用全波形地震动模拟
  • 拓展至不同诱发因素（如降雨诱发滑坡）

摘要

数十年来，区域尺度的滑坡预测解决方案主要依赖于数据驱动模型，这些模型本质上与滑坡失效机制的物理原理相脱节。这类工具的成功和广泛应用源于其能够利用代理变量而非明确的岩土参数，因为后者在广阔区域中难以获取。我们的研究采用了一种物理信息神经网络（Physics-Informed Neural Network, PINN）方法，通过在标准数据驱动架构中增加一个中间约束，用于解决Newmark边坡稳定性方法中典型的永久变形问题。这转化为一个神经网络任务，即从常见的代理变量中显式检索岩土参数，并针对可用的同震滑坡清单最小化损失函数。结果令人鼓舞，因为我们的模型不仅在标准易发性输出方面表现出色，还在过程中生成了区域尺度上预期的岩土属性地图。因此，这种架构旨在解决同震滑坡预测问题，如果在其他研究中得到验证，可能会开启基于PINN的近实时预测的可能性。

关键词：物理信息神经网络 滑坡预测 区域化边坡稳定性 深度学习

1. 引言

滑坡是一种典型的次生地质灾害，主要由两类地球系统过程触发：固体地球过程与水文过程。固体地球过程诱发的滑坡通常由地震、火山活动及其他地球物理现象引发，而水文过程则主要通过地下水位变化和地表水饱和作用触发滑坡（C.D.C., 2019）。无论何种诱因，滑坡均源于潜在滑动面上的应力或“驱动力”增大，这些力通常被称为触发力（Newmark, 1965；Jibson, 1993；Fan 等, 2019）。滑坡的全球分布导致了巨大的基础设施损失和人员伤亡（Petley, 2012；Fidan 等, 2024）。此外，随着气候变化情景下水文诱发滑坡频率增加（Gariano 和 Guzzetti, 2016；Dahal 等, 2024a）以及在人类开发活动导致的固体地球诱发滑坡易发区暴露度提升（Reichenbach 等, 2018；Wang 等, 2024a），这一趋势预计还将加剧。因此，滑坡的准确可靠建模已成为持续关注的重要研究方向。

在地震诱发滑坡中，本质上是因地震动对原本稳定边坡产生扰动，最终导致破坏（Gorum 和 Carranza, 2015）。一般而言，地震滑坡危险性建模需识别并估算使边坡失稳所需的地震动条件（Jibson, 2011）。这类方法可大致分为两类：基于物理机理的模型与数据驱动模型（Fan 等, 2019）。其中，基于物理机理的模型通过已知岩土参数及触发力求解物理系统正演问题（Memon, 2018），而数据驱动模型则基于统计与机器学习方法，利用显式或潜在解释变量来模拟滑坡发生（Amato 等, 2023）。

基于物理的滑坡建模自土力学理论诞生以来便已确立（Terzaghi, 1950），其核心是基于力平衡原理求解。针对地震诱发滑坡，Jibson (2011) 将此类方法分为三类：拟静力法、应力变形法与永久变形法。
拟静力法（Terzaghi, 1950）将地震动等效为作用在静态极限平衡图上的永久体力，当地震动产生的驱动力超过抗力时，边坡即发生破坏。尽管该方法直观简便，且应用历史悠久，但其仅能判断边坡稳定或破坏，无法估计不稳定后的后果或破坏概率（Jibson, 2011）。
应力变形法基于 Clough (1990) 提出的有限元方法，通过计算地震动作用下因土体刚度降低而引发的应力变化与变形，确定潜在破坏面（Memon, 2018）。该方法计算复杂、需详细岩土参数，但能自然演化破坏面，是当前最为真实的坡体破坏模拟方式（Jibson, 2011）。
永久变形法最早由 Newmark (1965) 提出，后经 Jibson (1993) 简化，介于前两者之间，兼具相对合理精度与适中数据需求。该方法将滑坡视为位于已知临界地震加速度斜坡上的刚性块体，当地震扰动超过该加速度，斜坡开始位移，达到一定位移阈值后即视为破坏。若已知边坡几何、土体性质与地震动参数，该方法预测效果良好（Jibson, 1993；Hsieh 和 Lee, 2011）。
然而，所有基于物理的模型均需空间异质性的详细岩土参数（如黏聚力、内摩擦角、密度、厚度等）（Fan 等, 2019），这在单个或少数边坡上尚可实现，但在区域尺度应用则极具挑战。

数据驱动滑坡建模方法主要分为统计方法与机器学习方法（Dahal 和 Lombardo, 2023）。统计方法基于环境变量，估算滑坡概率、频率或强度，变量形式可显式或潜在表达（Lombardo 等, 2019）。常用方法包括二元模型、逻辑回归、广义线性模型、广义加性模型及 Cox 过程等（Atkinson 和 Massari, 1998；Brenning, 2008；Yalcin, 2008；Steger 等, 2016a；Lombardo 等, 2020；Yadav 等, 2023）。尽管数学形式各异，这些方法本质上均旨在识别自变量与因变量间的显著统计关系，因变量通常表示滑坡发生（易发性）、频率或强度（如体积、面积、冲击力）（Dahal 等, 2024c,a）。模型通过极大似然或最小化损失函数拟合，力求预测值与观测值尽可能接近（Taylor 和 Diggle, 2014）。拟合完成后，须通过独立数据集验证预测能力，确保未来应用可靠性（Steger 等, 2016b）。

机器学习方法与统计方法原理类似（Jackson, 1988），不同之处在于，机器学习不预设明确的函数形式，能够表达潜在高度非线性关系（Dahal 等, 2024a）。深度学习方法主要通过最小化损失函数优化（Yang 等, 2019），模型架构与优化策略近几十年不断完善，显著提升了模型性能。当前滑坡灾害建模中常用的机器（深度）学习模型包括人工神经网络（ANN）（Gomez 和 Kavzoglu, 2005）、循环神经网络（RNN）（Fang 等, 2023）、Transformer（Dahal 等, 2024b）以及卷积神经网络（CNN）（Dahal 等, 2024c）。

然而，数据驱动方法主要问题在于未能遵循滑坡发生的物理机制，且神经网络往往对特定训练数据依赖性强，难以推广至其他区域，原因是缺乏对变量函数依赖关系的物理认知（Dahal 和 Lombardo, 2023）。同样，基于物理的方法由于动态岩土参数获取困难，区域尺度应用受限（Fan 等, 2019）。此外，岩土参数还受局地气候条件影响，如长期降雨或干旱（Kramer, 1996）。因此，亟需一种能够基于潜在变量推断滑坡发生，同时尊重其物理过程的建模框架。

目前，关于物理约束神经网络（Physics-Informed Neural Networks, PINN）的滑坡研究仅有两篇（Liu 等, 2023；Moeineddin 等, 2023）。此类模型位于物理与数据驱动模型之间，神经网络作为求解器，同时需学习滑坡破坏机制物理规律，而非单纯基于输入预测滑坡存在/不存在（Raissi 等, 2019）。其中，Liu 等 (2023) 利用 scoop3d 模型（Reid 等, 2015）标记非滑坡位置（伯努利分布中的0值），据此宣称其模型具物理约束性。尽管该方法方向正确，但严格来说仍未完整符合 PINN 定义，因为模型未正式融入物理方程，仅是以物理方式约束数据，神经网络需从 scoop3d 模拟结果中“学出”物理过程，因此缺少标准 PINN 的核心要素。
Moeineddin 等 (2023) 则正确将滑坡蠕变机制嵌入建模框架，符合 PINN 定义。但该方法仅能在具备岩土参数的特定单一边坡求解偏微分方程，无法推广至区域尺度。换言之，除非定义出可推广的 PINN，否则传统数据驱动方法的优势仍不可替代。

本研究旨在开发一种具物理约束、可区域尺度推广的通用 PINN。方法上，将岩土参数视作深度学习模型中的潜在变量，先基于环境因子估算，再将估算参数用于建模滑坡易发性及地震动扰动效应。后文将依次介绍研究区与数据（第2节）、方法框架（第3节，采用严格数学形式，便于今后学者复现）、结果（第4节）、讨论（第5节）及未来展望（第6节）。

2. 数据与测试区概述

为了训练和评估本文提出的 PINN 模型，我们选用了 Dahal 和 Lombardo（2023）公开发布的数据集。研究区位于尼泊尔，曾在 2015 年经历了 7.8 级 Gorkha 地震，诱发了数以万计的同震滑坡（见图 1a）。这些滑坡由 Roback 等（2017）编制成了一套可公开获取的滑坡清单。由于采用了人工解译与超高分辨率光学影像相结合的方法，该滑坡清单被 Schmitt 等（2017）与 Tanyaş 等（2017）公认为全球同类资料库中质量（Tanyaş 和 Lombardo，2019）与完整性（Tanyaş 和 Lombardo，2020）均处于领先水平的成果之一。

本研究区位于尼泊尔，地貌环境极为崎岖，受喜马拉雅山脉影响，坡度变化范围为 5°–80°，高差变化从约 500 m 至 5000 m 不等。值得注意的是，Gorkha 地震发生在尼泊尔旱季，地下水对浅层滑坡（Roback 等人报道的主导机制）的贡献可认为微不足道（Regmi 等，2016）。不过，虽然前几个月仅有零星降水，降水对植被状况和土壤含水率仍具影响，进而可能诱发不同类型的滑坡。因此，尽管降水不足以显著抬升地下水位，我们仍将其纳入预测因子体系中。

本次试验区主要出露的地层为 Siwalik 组，其次为 Himal 组，以及 Seti 和 Sarung Khola 等多种河流地层（Dahal，2012）。其中，Siwalik 组主要由喜马拉雅 Molasse 沉积组成，包含砂岩、泥岩、页岩和砾岩（Upreti，2001）。中喜马拉雅地区的河流地层以片岩、花岗岩、片麻岩、千枚岩和石英岩为主（Upreti，2001；Dahal，2012）。而上喜马拉雅区域则以受强烈构造压缩影响的变质岩为主，包括片岩、片麻岩、混合岩和大理岩（Upreti，2001）。本研究所用的地质图来自 Wandrey（1998），将研究区划分为九个地质类型单元，预测因子用地质图见图 1-b。

本研究所采用的制图单元为坡单元（Slope Units，简称 SU）。SU 本质上是沿主流域坡面方向划分的半子流域，具备整体坡向一致的特点（Alvioli 等，2016）。SU 在滑坡研究中多用于数据驱动模型（如 Tanyaş 等，2019），仅有 Domènech 等（2020）在后处理阶段将其应用于基于物理的斜坡稳定性模型。本研究旨在利用 SU 来表征“无限边坡”问题（Xiao 等，2016；Xi 等，2024）。区域性研究中，SU 被普遍认为是最佳的空间划分方式，能较好地地理近似丘陵坡面的失稳响应特性（Alvioli 等，2020）。同样的地貌学依据在本 PINN 模型架构中依然成立，且 SU 的坡面同质性特点也符合伪静力法和永久变形法分析所假设的斜坡均匀性（Newmark，1965）。

在定义 SU 时，我们曾考虑采用 Alvioli 等（2022）为整个喜马拉雅地区划分的 SU，但由于其空间尺度过大，无法满足本模型需求，最终选用了 Dahal 和 Lombardo（2023）采用的小尺度划分方案。该方案通过 r.slopeunits 参数化（参见 Alvioli 等，2016）多版本划分组合并经人工检视筛选确定。每个 SU 均作为本研究汇总预测因子和滑坡稳定/不稳定标签的空间尺度。滑坡与非滑坡单元的判定方法为，将滑坡滑动区（不含堆积区和泥流区）叠置于 SU 单元，若滑动区落入 SU 范围内，则该 SU 判定为发生滑坡，否则视为未发生滑坡（见图 1-a）。

为便于理解，以下简要总结了本研究选取的预测因子及其选取依据，各因子详细分布图见附录图 1：

1. 东向性（Eastness）：表示坡面朝东的程度，完全朝东值为 1，完全背离东向值为 0，间接表征坡面受光照强度，对滑坡发生具潜在影响（Olaya，2009）。
2. 北向性（Northness）：类似于东向性，反映坡面朝北的程度，作用相同（Olaya，2009）。
3. 水平曲率（Horizontal Curvature）：衡量坡面相对于假想水平切线的“水平弯曲度”，是坡面三维几何形态的代理指标（Hengl 和 Reuter，2008）。
4. 垂直曲率（Vertical Curvature）：衡量坡面相对于垂直铅垂线的“垂直弯曲度”（Hengl 和 Reuter，2008）。
5. 坡度（Slope）：衡量坡面的陡峭程度，是控制滑坡发生的重要一阶因子，因为重力作用始终沿坡面方向影响物体稳定性（Hengl 和 Reuter，2008；Lombardo 等，2019）。
6. 降水量（Precipitation）：表示地震发生前三个月内，各 SU 区域累计降水量，间接反映坡面相对湿润度和潜在的浅层破坏面状态（Moore 等，1991）。
7. 植被指数（NDVI）：反映区域植被状况，间接表征植被根系抗滑强度。
8. 峰值地面加速度（PGA）：反映地震动扰动强度，是控制地震诱发滑坡的重要一阶因子（Dahal 等，2023）。
9. 砂、粉、黏含量（Sand, Silt, Clay Content）：反映 SU 上方 2 米土层中三种粒径组分的平均含量，对浅层滑坡至关重要。因实测困难，引用 Hengl 等（2017）基于全球土壤样本与机器学习模型的预测数据，虽存在一定不确定性，但区域尺度下依然是可接受的代表性数据。
10. 容重（Bulk Density）：即土壤烘干状态下的单位体积质量，反映潜在破坏面和破坏物质的物理性质，同样来自 Hengl 等（2017）的全球推算数据。
11. 地质类型（Geology）：与地震动、坡度同为滑坡发生的重要一阶控制因子，提供 SU 区域的地质构造信息，不同地质单元与滑坡发生概率及类型有显著关联（Dahal，2006；Wandrey，1998）。

3 方法

滑坡易发性（Landslide susceptibility）可定义为在特定位置和时间下滑坡发生的概率 KaTeX parse error: Undefined control sequence: \[ at position 13: L(s, t) \in \̲[̲0, 1]，其中 $L(s,t)=1$ 表示发生滑坡（Fell et al., 2008；van Westen et al., 2008）。在评估某一区域发生边坡失稳的倾向性时，通常采用历史滑坡清单（Maharaj, 1993）或事件性滑坡清单（Lombardo and Tanyas, 2020），但这常常忽略了滑坡发生的时间因素。因此，易发性通常被空间定义为 $\mathcal{X}\_s$，其表示形式可简化为 $L(s)=1$。我们再次强调，易发性通常通过基于物理的方法或数据驱动方法获得（Fan et al., 2019）。

在物理方法中，易发性 KaTeX parse error: Undefined control sequence: \[ at position 13: p\_p(s) \in \̲[̲0, 1] 定义为在给定地质力学条件 $G(s)$ 下，任意位置 $s$ 处的位移 $D$ 超过某一最小位移阈值 $d\_p$（或某些情况下为速度）的概率（Huang et al., 2020）：

$$p_p(s)=\mathrm{Pr}(D(s)\ge d_p\mid G(s)=x(s))$$

但在很多情况下，变量 $G(s)$ 无法在区域尺度上获取，因此物理方法在区域尺度应用时，通常将这些变量简化，假设研究区域 $\mathcal{X}\_s$ 内地质力学性质恒定（Fan et al., 2019）。

在这一背景下，数据驱动模型提供了可行的替代方案。统计模型可基于一组预测因子，直接推断随机过程的概率，进而估计在环境条件 $X(s)$ 下滑坡发生（$L(s)=1$）的概率（Dahal et al., 2024a）。考虑到 $L(s)=1$ 的二元性质，伯努利分布非常适用于该分类任务，概率分布记为 $L(s)\sim \mathrm{Ber}(p\_d(s))$。因此，滑坡发生概率 KaTeX parse error: Undefined control sequence: \[ at position 13: p\_d(s) \in \̲[̲0, 1] 可表示为：

p d ( s ) = Pr ⁡ { L ( s ) = 1 ∣ X ( s ) = x ( s ) } p_d(s) = \Pr\{L(s) = 1 \mid X(s) = x(s)\} pd​(s)=Pr{L(s)=1∣X(s)=x(s)}

然而，以上两种体系存在根本差异。数据驱动方法中，$X(s)$ 往往不能准确代表滑坡发生时真实的地质力学条件，且模型本身也不遵循滑坡过程的物理机理（Dahal and Lombardo, 2023）。因此，数据驱动方法更适合作为滑坡灾害的一阶估算工具，可用于筛选高易发性区域，再通过物理方法进一步分析。

但该序列存在两个主要问题：第一，若数据驱动方法将部分高易发性位置误判，或存在 II 型错误，则后续分析可能遗漏危险区；第二，这种理想流程仅适用于灾前预判，而在应急救援阶段则不切实际。强震诱发大范围滑坡时，只能实现近实时的滑坡易发性评估（Jessee et al., 2018），无法进行详细分析（Mon et al., 2018）。

为解决上述问题，本文提出融合两者优势的单一模型，兼具区域尺度预测、地质力学解释性以及预训练后的近实时预测能力。方法是通过深度学习非线性函数 $F$，由环境变量 $X(s)$ 估计地质力学参数 $G(s)$：

$$G(s)=F(X(s))\mid X(s)=x(s)$$

再将估计得到的 $G(s)$ 传入物理模型计算滑坡易发性。

本研究中，神经网络函数 $F$ 采用简单架构，包含 16 个神经网络块。每个块为一个包含 64 个神经元的全连接神经网络，末尾块包括批归一化层（Ioffe and Szegedy, 2015）、丢弃层（丢弃率 0.3，Srivastava et al., 2014）和 ReLU 激活函数（Yarotsky, 2017；Nair and Hinton, 2010）。权重与偏置通过正态分布随机初始化（Thimm and Fiesler, 1995）。批归一化与丢弃层用于防止过拟合，ReLU 激活将模型转化为非线性形式。最后一层的神经元数等于所需估计的地质力学参数数量，此处为 2 个。

输入该模型的数据为所有影响滑坡稳定性的环境因子 $X(s)=x(s)$，通过神经网络逐层处理后，输出 $G(s)$，再传入物理计算模块。

在物理层面，我们选取适用于震触发滑坡的永久位移方法（Newmark 法，Jibson, 2007；Gallen et al., 2015）。Newmark 方法定义滑坡易发性为地震扰动下永久位移的函数（Newmark, 1965）。

假设无地震扰动时，边坡的安全系数取决于地质力学参数和几何条件。影响安全系数的参数包括：土体黏聚力 $C$、滑动块厚度 $t$、岩土密度 $\rho \_r$、水密度 $\rho \_w$、内摩擦角 $\varphi$、滑动面坡度 $\alpha$、饱和厚度与总厚度比值 $m$，以及重力加速度 $g$。Gallen 等（2015, 2017）将安全系数公式定义为：

$$FS=\frac{C}{tm({\rho }_{r}g)\sin (\alpha )}+\frac{\tan (\varphi )}{\tan (\alpha )}-\frac{m({\rho }_{w}g)\tan (\varphi )}{({\rho }_{r}g)\tan (\alpha )}$$

鉴于 Gorkha 地震发生在喜马拉雅旱季，假设地下水位低于滑面，$m=0$（Gallen et al., 2017），公式得以简化。

同时，区域内岩土密度取常数 $\rho \_r=2300kg/{\mathrm{m}}^3$。原因是该区域绝大部分地质类型相同，且不同风化程度岩土缺乏密度数据。与其在未知代表性前提下引入微小密度差异，不如固定密度值，让模型通过砂、粉、黏粒含量、容重和地质类型学习地质力学参数变化。同理，重力常数 $g=9.8m/{\mathrm{s}}^2$。

安全系数分子项代表坡体抗滑强度，可转换为滑动块在斜面上发生滑动所需的临界加速度 $a\_c$（Jibson, 1993）：

$$a_c=(FS-1)g\sin \alpha$$

加入地震动峰值加速度 $a\_p$ 后，可利用 Jibson (2007) 和 Gallen 等 (2015, 2017) 提出的经验模型计算滑动块的 Newmark 位移 $D(s)$：

$$\log D(s)=0.215+\log \left[{\left(1-\frac{a_c}{a_p}\right)}^{2.341}{\left(\frac{a_c}{a_p}\right)}^{-1.438}\right]\pm 0.51$$

上述公式（(1)、(2)、(3)）组合成物理层函数 $\psi$，输入包括环境变量中的坡度 $\alpha (s)\in X(s)$ 和峰值加速度 $a\_p(s)\in X(s)$ 及神经网络估计的地质力学参数 $G(s)$。其中 $G(s)$ 包含黏聚力与厚度比值 $C/tm$ 和内摩擦角 $\varphi$。$\psi$ 返回永久位移项的指数值 $\exp (D(s))$。

需注意，$G(s)$ 为物理量，存在已知的合理范围，因此采用数值裁剪方法，将其限制在区间 KaTeX parse error: Undefined control sequence: \[ at position 1: \̲[̲0, 60] 度（$\varphi$）和 KaTeX parse error: Undefined control sequence: \[ at position 1: \̲[̲5, 40] \ \mathr…（$C/tm$）内。这一做法有两点好处：其一，估计值符合物理模型边界条件；其二，避免因非现实数值导致梯度爆炸或消失。

最终，位移模型表示为：

$$D(s)=\psi (G(s),\sigma (s),a_p(s))$$

由于我们无法观测滑坡体的中间变形，仅知其是否滑动，因此设定 5 cm 为判别阈值，超过即视为滑坡（Wieczorek et al., 1985；Gallen et al., 2017）。

然而，上述方法仍然无法直接提供滑坡发生的概率（或易发性），而是以二元分类的形式表达滑坡过程。因此，我们对人工神经网络（ANN）中的 sigmoid 函数 $\varsigma$ 进行了改造，使其围绕 $5,\text{cm}$ 的位移阈值居中，从而输出物理信息约束的数据驱动型滑坡易发性 KaTeX parse error: Undefined control sequence: \[ at position 10: p(s) \in \̲[̲0,1]，具体表达式为：

$$p(s)=\varsigma (D(s))=\frac{1}{1+e^{(5-D(s))}}$$

即式 (4)。该公式与传统 sigmoid 激活函数类似，但以 $5,\text{cm}$ 为中心，对 $D(s)\gg 5,\text{cm}$ 的情况赋予较高概率，对 $D(s)\ll 5,\text{cm}$ 的情况赋予较低概率。该函数的图形化形式见图 2。

因此，整个基于物理信息集成的滑坡易发性模型可表示为：

$$p(s)=\varsigma (\psi (F(X(s)),\sigma (s),a_p(s)))\mid X(s)=x(s),\sigma (s)\in x(s),a_p(s)\in x(s)$$

进一步简化表示为：

$$\Theta (X(s))\mid X(s)=x(s)$$

该模型结构、损失函数与反向传播过程见图 3。此处需强调，所有神经网络结构均依赖损失函数来收敛至最优解。因此，为训练模型 $\Theta (X(s))$ 中的可训练部分，我们采用二元交叉熵损失函数（Good, 1963；Akaike, 1998），因为模型输出是伪概率值 KaTeX parse error: Undefined control sequence: \[ at position 10: p(s) \in \̲[̲0,1]。具体写作式 (5)：

Loss = − ∑ i ∈ BN { l i log ⁡ ( p i ( s i ) ) + ( 1 − l i ) log ⁡ ( 1 − p i ( s i ) ) } \text{Loss} = - \sum_{i \in \text{BN}} \left\{ l_i \log(p_i(s_i)) + (1-l_i) \log(1-p_i(s_i)) \right\} Loss=−i∈BN∑​{li​log(pi​(si​))+(1−li​)log(1−pi​(si​))}

其中，$l\_i$ 为第 $i$ 个坡单元在地震事件期间的实际滑坡发生值，$p\_i(s\_i)$ 为该坡单元的预测发生概率。训练过程中，我们采用小批量（mini-batch）随机优化策略，将训练样本划分为 $N<n$ 的小批量 $\text{BN}\subset 1,\dots ,n$，其中 $n$ 为总样本量（Li et al., 2014）。

总结该模型及训练策略：首先将第 2 节定义的环境变量作为输入，传递至神经网络模型（见图 3），神经网络初始估计一组随机地质力学参数，随后将这些参数输入 Newmark 方法计算滑坡易发性。模型输出的易发性再与实际滑坡分布进行比较，根据损失函数计算误差，并通过反向传播不断更新神经网络参数，直到模型学会估计足够合理的地质力学参数，从而生成与实际滑坡分布相近的易发性结果。

在该损失函数和模型设定下，训练集占数据总量 70%，剩余 30% 数据分成一半用于验证模型，另一半用于测试。优化器选用 Adam（Kingma and Ba, 2014），因其在深度神经网络训练中的鲁棒性表现优异。初始学习率设为 $1\times 10^{-3}$，每训练 10000 个小批次后将学习率降低 90%。批次大小设为 1024，表示每次迭代随机选取 1024 条训练数据送入模型。

模型性能通过传统受试者工作特征曲线（ROC）下的面积（AUC）、平衡准确率（balanced accuracy）及 F1 分数（Thibos et al., 1979；Goutte and Gaussier, 2005）评估。此外，为验证模型稳定性，执行 10 折交叉验证，每次随机抽取九成数据训练，剩余一成测试。鉴于二元分类模型的空间相关性特性，纯随机抽样交叉验证可能导致乐观偏倚（Brenning, 2012），因其未打破数据中的空间结构，从而交叉验证结果可能接近整体拟合结果。为此，文献建议采用空间交叉验证以全面评估预测性能（Pohjankukka et al., 2017）。空间交叉验证基于坡单元地理位置分组，确保空间相关性被打破，从而获得无偏性能评估。

因此，本文同样引入了 10 折空间交叉验证，将坡单元数据划分为 10 个空间簇，每次选取其中 9 个簇训练，1 个簇测试。具体簇划分方法参见 Dahal and Lombardo (2023) 中图 3，本文沿用相同划分方式。

除性能评估外，本文模型的核心优势在于地质力学参数可解释性。因此，不仅输出滑坡易发概率 $p(s)$（即易发性分布图），还可输出模型估算的地质力学参数 $G(s)$，以及模型对各坡单元估计值的置信水平。

在我们定义的 PINN 模型结构中，这些参数为坡体黏聚力与滑移块体厚度之比 $C/t\_m$ 以及内摩擦角 $\phi$。同时，由于模型包含多个“层”，我们可逐层提取影响地震诱发滑坡的关键控制参数。例如，可提取临界加速度 $a\_c$，判断坡体发生滑坡所需最小地震激励强度。该参数由坡度和材料强度共同决定，由神经网络模型输出。

同样，地质力学参数 $C/t\_m$ 和 $\phi$ 可通过神经网络最后一层在进入“物理层”之前、在给定环境条件下提取。但考虑到区域尺度分析，地质力学参数本身存在一定的不确定性，必须评估模型估计结果的可靠性。

为评估不确定性，本文采用自助法（bootstrap）对整体数据集进行 50 次抽样，每次随机选取 50% 数据训练模型，剩余数据用于估计。这样可获得 50 个不同训练模型，检验模型在未见数据上的物理合理性及结果一致性。由于每个深度学习模型训练结果略有差异，能由此估计模型输出地质力学参数的内在不确定性。

最终，我们预测出每次 bootstrap 模型估算的地质力学参数值，提取其中位数、第 5 百分位数和第 95 百分位数，从而为每个坡单元提供一组地质力学参数分布的统计汇总结果。

4. 结果

本节展示了模型在空间和随机交叉验证下的性能评估结果、中间岩土参数以及滑坡易发性结果。我们采用了两种主要方法对模型进行评估。首先，使用 ROC 曲线及其曲线下面积 (AUC) 值，其中根据多个阈值及其对应的真正率和假正率绘制 ROC 曲线。其次是 F1-Score 和平衡精度 (balanced accuracy) 指标，这可以更全面评估模型预测精度，因为在许多情况下，单独依赖 ROC 和 AUC 往往会高估模型性能。总体而言，我们的 PINN 模型取得了优异的性能表现（参见 Hosmer 和 Lemeshow, 2000 提出的分类标准），AUC 值达到了 0.87。

为了完整评估模型性能，我们还计算了以 0.5 为概率阈值时的平衡精度和 F1-Score 值，考虑到数据集存在不平衡的情况，这样可以使模型表现相对平衡。评估结果分别为 0.79 和 0.78。这表明基于整体数据集构建的参考模型，能够准确区分稳定与不稳定的坡单元 (SU)。

图 4 补充展示了两种交叉验证方案的性能评估结果。随机交叉验证的结果展示于图 4 的 panel (a) 混淆图 (Titti et al., 2022) 和 panel © 中对应的 ROC 曲线及 AUC 值。从图中可以看出，模型能够预测 10 折随机交叉验证过程中大部分滑坡发生位置。除了少数暗红色和暗蓝色的位置外，大部分区域与观测数据拟合良好。聚焦于假阳性和假阴性，它们主要集中在发生滑坡和未发生滑坡坡单元簇的过渡带。这反映出接近优异的分类性能，K 折随机交叉验证的 AUC 值分布在 KaTeX parse error: Undefined control sequence: \[ at position 1: \̲[̲0.86, 0.90] 范围内。

类似地，图 4 还报告了空间交叉验证产生的混淆图 (panel b) 及其对应性能 (panel d)。即便如此，大部分误分类的坡单元仍集中在滑坡发生簇和未发生簇的过渡区域。对比这两张混淆图，虽然总体模式基本一致，但空间交叉验证的性能波动更大，AUC 值在 KaTeX parse error: Undefined control sequence: \[ at position 1: \̲[̲0.69, 0.89] 之间。

由于我们沿用了 Dahal 和 Lombardo (2023) 中的相同数据和交叉验证结构，因此可以将本研究结果与前人基于标准 ANN 模型的结果进行对比。比较随机交叉验证下的混淆图，当前方法和前人研究预测模式相似。需要强调的是，深度学习方法的目标是最大化预测性能，因此即使模型未整合任何物理过程，也能取得较好表现，这也是深度学习方法如今被广泛应用的原因。

但最有趣的发现来自于本研究与 Dahal 和 Lombardo (2023) 混淆图的对比。此前的模型由于未纳入物理机制，导致研究区东南部出现大量假阳性。而我们基于 PINN 的结果则没有此问题。同样从预测性能来看，当前空间交叉验证中最差的 AUC 值为 0.69，而标准神经网络模型在相同折次下仅为 0.58。我们希望特别强调这一点，并在第 5 节进一步探讨标准神经网络与物理信息神经网络的对比。

与仅提供预测性能评估和最终结果的数据驱动模型不同，我们的框架还能展示估计得到的岩土工程参数。我们在图 5 和图 6 中展示了基于 Bootstrap 的单位厚度抗剪强度 ($c/t$) 和内摩擦角 ($\phi$)。$c/t$ 和 $\phi$ 的值在第 5 和第 95 百分位上均出现饱和值现象。这是由于这两个百分位位于分布的两端，难以代表参数分布的主体部分。尽管这两个百分位值的空间变化较少，但其数值范围仍处于物理量常规合理范围内（Gallen et al., 2017），表明模型运行过程符合物理过程边界条件。

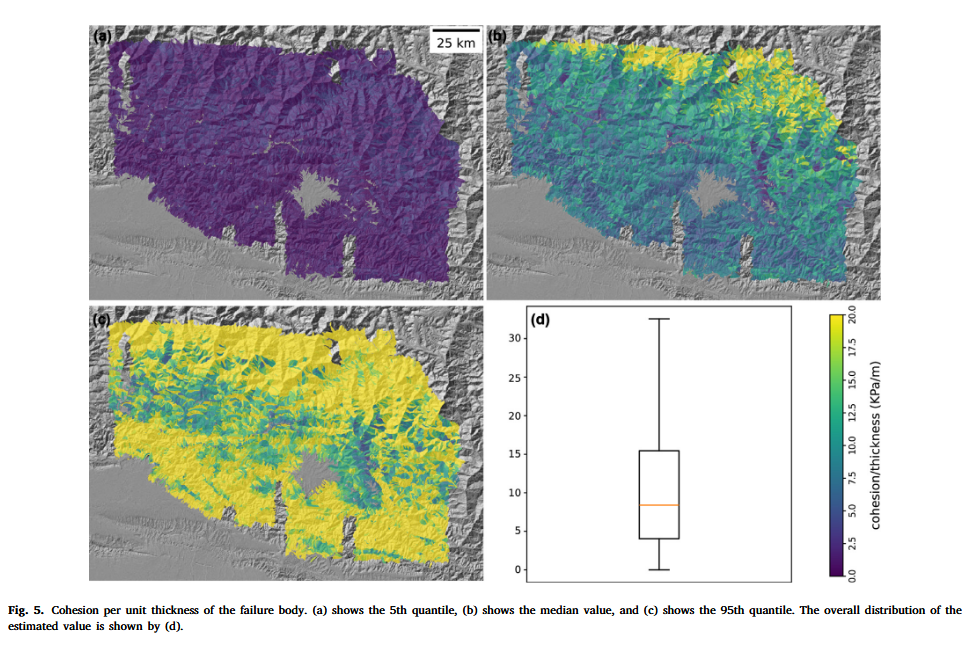
仔细观察中位数结果，发现 $c/t$ 值在喜马拉雅山脉北部（上喜马拉雅区）较高，表明该区域以岩质材料为主。反之，在中喜马拉雅和下喜马拉雅地区，$c/t$ 值逐渐减小，这与覆土层厚度增加相符。有趣的是，一些流域表现出极低的 $c/t$ 值，可能间接表明滑体厚度较大或潜在滑动面较深。总体上，$c/t$ 的空间分布趋势较为饱和，几乎不受百分位影响，这很可能是因为取 $c$ 与 $t$ 的比值后，$t$ 将参数分布拉平，减弱了空间差异性。

而 $\phi$ 的情况不同，如图 6 所示，其空间变异性明显更高，且上、中、下喜马拉雅区呈现合理的分布格局。上喜马拉雅区表现出较高的内摩擦角，而滑坡发生的坡单元则对应较低的内摩擦角。

为了进一步理解预测结果，我们在图 7 中展示了临界加速度和通过主模型获得的滑坡易发性分布图。临界加速度表示触发某坡面失稳所需的最小地震动强度。该参数的空间分布基本随机，取决于各坡面的岩土参数与坡度。尽管部分坡单元的临界加速度值表现出与低易发性坡单元相匹配的空间格局，但总体而言并无明显规律。关于临界加速度的进一步讨论将在第 5 节展开。

至于滑坡易发性分布图，可以看到大部分滑坡发生在中喜马拉雅区，该区域被判定为高易发性区。向南延伸，滑坡易发性逐渐降低，只有少数坡单元簇呈现较高滑坡易发性。

5. 讨论

本研究开发的模型或可作为滑坡灾害建模的一种有价值的替代方案，因为相较于传统的数据驱动方法，它具备一系列优势。首先，正如 PINN（Physics-Informed Neural Network，物理信息神经网络）定义所暗含的那样，模型能够遵循地震诱发滑坡失稳过程的物理机理。其次，PINN 将岩土工程参数视为潜变量（latent predictors），通过数据反演得到这些参数。通常，许多基于物理的方法的弱点恰恰在于其对明确岩土工程信息的依赖，因此这类方法要么只能应用于地理范围有限的小区域，要么在大区域内预测能力不足。这是因为在区域尺度上获取岩土工程数据代价高昂，难以实现。因此，当这些方法用于区域性边坡稳定性分析时，往往需要对参数取值作简化假设，例如假定整个研究区内采用相同的岩土参数值（Fan et al., 2019）。

而在另一个极端，数据驱动模型通常难以在单个边坡或少数流域范围内有效工作，因为滑坡目录（inventory）中若滑坡数量有限，便难以支撑稳定/失稳边坡与预测因子之间的统计关系构建。一般而言，大规模的滑坡目录通常来自更大区域，除非某次极端诱发事件在局部产生大量滑坡（例如 Görüm et al., 2023；Santangelo et al., 2023）。换言之，尽管理论上数据驱动方法对滑坡数量没有严格下限，但若仅有数十条滑坡记录，显然无法可靠建立统计模型。这也是为何现有数据驱动滑坡易发性模型多应用于区域（如 Wan, 2009；Frattini et al., 2010；Lin et al., 2018）、国家（如 Trigila et al., 2013；Lima et al., 2017；Wang et al., 2022）乃至全球尺度（如 Jia et al., 2021；Felsberg et al., 2022；Tang et al., 2023）之中。然而，尽管数据驱动模型具有优异的预测性能，但通常缺乏物理一致性（Glade et al., 2005）。迄今为止，较好的做法是通过统计模型解释回归系数（Steger et al., 2022, 2024），或对机器学习模型提取预测因子重要性（Di Napoli et al., 2020；Meena et al., 2022），以及近年来常用的 SHAP 值（Collini et al., 2022；Wang et al., 2024b）分析。

因此，我们强调本研究所提出的建模方法可视为朝着结合物理基础与数据驱动模型、获得物理一致性、具备区域尺度推广性且可靠的滑坡易发性评价结果迈出的重要一步。传统 PINNs 用神经网络求解物理问题，尽管其精度通常不及有限元等数值方法（Grossmann et al., 2023），但计算速度快，且对训练样本数量要求较低。另一方面，目前一些通过数百万基于物理假设的数值模拟生成样本，训练出的模型虽然形式上借助了物理，但本质上仍是数据驱动模型，其泛化能力与典型数据驱动方法面临相同的问题。

在本研究中，我们并未直接求解滑坡力学的偏微分方程（如流变方程），因为缺乏足够的区域性岩土工程数据及滑坡变形观测数据，难以通过 PINN 在区域尺度解算该类问题。但我们实现了在已知滑坡发生结果的基础上，结合环境与地质因子，反演推断岩土工程参数。由于滑坡过程遵循一定物理规律，我们可将这些规律以约束形式加入损失函数，通过反演方法估计给定地质与环境条件下的岩土工程参数。一旦模型充分训练完成，即使环境条件发生变化（如降雨、植被覆盖变化），模型也具备估算参数的能力。这一方法赋予模型一定物理约束，但尚未达到通过 PINN 求解偏微分方程的程度，是迈向区域尺度滑坡灾害物理信息神经网络建模的重要探索。

在方法实现上，我们将 Newmark（1965）提出的永久变形法嵌入深度学习模型中，反演其相关参数，类似于将地震动扰动作用叠加至 Terzaghi（1950）静力极限平衡方法中，从而模拟地震扰动诱发的失稳。本方法当前适用于浅层滑坡场景，因为忽略了地下水位因素，且研究区内滑坡均属浅层滑坡。若应用于其他类型滑坡，需相应调整控制方程及物理模型。

另一个本方法解决的问题是，即便某些区域能获得可靠的区域性岩土工程参数（据我们所知，目前仅在美国 Northridge 地区有类似数据，Dreyfus et al., 2013），这些参数也仅代表采样点当时条件，且常受降雨、植被、人类活动等因素影响而变化。因此，基于物理的滑坡模型需频繁更新或重标定（Clarke and Burbank, 2011；Townsend et al., 2020；Singeisen et al., 2022）。而我们的方法尝试估算地震触发前边坡的岩土工程状态，即神经网络反演得到的参数，反映滑坡发生前土体与边坡的物理状态。这在本研究中尤为合理，因为地震扰动是在模型后续步骤中施加，而不是一开始就作为输入条件。因此，虽然我们同样无法验证反演参数是否与地震前真实值完全一致，但由于模型在单个坡单元（SU）尺度提取参数，空间分辨率较高，可作为区域滑坡易发性评价中岩土工程条件定量化的一种便捷手段。

在坡单元尺度上，单点岩土参数的细微变化对整体结果的影响有限，因此理论上模型对参数波动的敏感性较低。即使存在这类问题，相较于系统性的野外调查，本方法无疑是一种成本更低、效率更高的区域岩土参数估算手段。

另一个值得讨论的重要点是，我们在模型中选择以 5 cm 为中心的 sigmoid 函数，而非像物理模型方法（如 Jibson, 1993）那样，使用 Heaviside 阶跃函数在 5 cm 处区分滑坡的存在与否。这是因为在采用二元交叉熵损失函数训练深度学习模型时，模型输出若为离散的 0 或 1，往往不利于优化过程的稳定与收敛。因此，引入 sigmoid 函数是必要的选择。

关于 5 cm 阈值的设定，实际上在自然界中，滑坡是否发生并不总是以 5 cm 的永久位移作为判断标准。在许多情况下，坡体稳定性并不能由某个固定值简单划分，已有诸多研究在不同情境下采用不同的阈值。考虑到深度学习和数据驱动领域通常将概率阈值设定为 0.5，并将大于 0.5 的概率判定为滑坡发生，小于 0.5 判定为未发生，因此我们决定将 5 cm 作为 0.5 概率阈值，意味着超过该位移值即具有潜在滑坡可能，低于该值则认为坡体尚未失稳。当然，位移小于 5 cm 并不代表坡体绝对稳定，裂缝的出现依然可能预示潜在滑坡风险。

需要注意的是，这种方法虽然具有优势，但在与标准深度学习架构的性能对比中，也存在局限性。PINN 通过引入物理定律作为额外的约束条件，通常会导致预测性能低于纯数据驱动、仅依赖环境因子进行拟合的神经网络模型。这是现有 PINN 相关技术文献中的普遍假设（参见 Cuomo et al., 2022）。由于我们与 Dahal 和 Lombardo (2023) 采用了相同数据，因此可将前人研究作为基线，对这一普遍假设进行验证。

有趣的是，在本研究中，无论是空间交叉验证还是随机交叉验证，PINN 模型的表现与此前实验相当，甚至有所提升。例如，在 10 折随机交叉验证结果（图 4）中，误分类的滑坡点主要集中在滑坡与非滑坡坡单元（SU）边界附近。这可能是因为在相似环境条件下，模型估算出的岩土工程参数值相近，加之地震动强度数据在空间上较为平滑，邻近坡单元受到的地震动特性相似。这类问题较难避免，源于物理约束方法与环境预测因子数据分布特性之间的耦合。因此，我们发现模型误分类主要集中在失稳坡单元与稳定坡单元的过渡区域。

而在空间交叉验证中，PINN 模型性能明显优于未嵌入物理约束的前人模型（Dahal 和 Lombardo, 2023），特别是在研究区东南部，PINN 几乎无误分类，而前人方法却在该区域存在明显误判。我们将其解读为模型空间可转移性（spatial transferability）的提升。换言之，当数据不足或性能导向型模型在新数据上预测时，PINN 因需遵循物理定律，提供了更可靠的估计结果。

从生成的研究区岩土参数反演结果来看，估算出的 $c/t$ 与 $\phi$ 在中位数空间分布图中呈现出显著空间差异，符合自然界岩土参数空间变异性特征，相较于单一取值假设更具现实意义。中位数值范围落在合理的岩土参数区间内，且表现出合理的空间变化特征，如喜马拉雅主山脉及 Siwalik 地区内部摩擦角 $\phi$ 较高，而土壤密实度较高的中喜马拉雅地区内部摩擦角较低。$c/t$ 的空间分布规律与之类似，但由于归一化至可能的滑动体厚度，差异性不如 $\phi$ 明显，因为浅层滑坡通常发生在低粘聚力土层，而高粘聚力材料通常对应较深滑动面。

在第 5 百分位图中，两个参数的空间变异性非常小，几乎趋于常数值。这种情况在 Gallen et al. (2015) 中曾用常数值解释滑坡密度分布，依然是现实可行的估计。在第 95 百分位图中，$\phi$ 基本处于饱和值，$c/t$ 也处于高值区间。这表明基于自助法（bootstrap）估算的岩土工程参数在中位数范围内合理，且具备作为默认值使用的潜力，此外也可基于全部估计值开展参数不确定性传播分析。

模型生成的临界加速度（critical acceleration）与滑坡易发性产品也表现出有趣特性。滑坡易发性产品的空间分布与实际滑坡目录高度吻合，易发性值在滑坡点与非滑坡点之间区分明显，反映出模型在滑坡易发性估计中的高置信度。尤为值得关注的是，临界加速度作为岩土参数与坡度的函数，其空间分布表面上呈现较随机态势，但在滑坡高发区内，非滑坡坡单元的临界加速度与滑坡坡单元表现相似。临界加速度表示坡体失稳所需的地震动强度，当实测地震动强度超过临界值后，滑坡易发性与滑坡密度相应升高。

将物理约束融入滑坡易发性建模，可为数据驱动方法开辟新路径。这一框架适用于极端气候或不同灾害场景下滑坡建模（Dahal et al., 2024a）。特别是传统 AI 数据驱动模型在训练域外泛化能力有限，而本研究表明，嵌入物理机制可有效改善这一问题。因此，未来可将该方法同时应用于降雨诱发滑坡和地震诱发滑坡（Cuomo et al., 2022；Maleki et al., 2022），应对不同气候与地质环境场景。

此外，具备数学与物理一致性的模型可提供可解释性优势，便于分析中间产品，判断模型行为是否合理。这种“人-机协同”的建模理念，对近实时滑坡易发性预测尤为重要，因为预测结果直接关系到后续应急响应决策（Dahal 和 Lombardo, 2023）。

尽管本研究提出了新的滑坡灾害建模框架，但仍存在局限性，有待后续改进。首先，所采用的数学/物理框架基于永久变形分析方法，其本质仍是对滑坡过程的简化，假设失稳沿固定滑面发生，且坡度恒定（Jibson, 2011）。然而，自然界中的坡面形态复杂，通常需通过坡单元划分简化坡度。此外，滑动面多为假设，而非实测。

应力-变形方法（stress-deformation approach）可根据应力-应变场自动形成滑动面（Griffiths 和 Lane, 1999），但需依赖应力参数及基于网格划分的有限元法，每个网格单元将自身应力-应变特性传递至相邻单元（Memon, 2018）。该方法在物理模型研究中较为常见，但由于浅层滑坡多在数秒内发生，缺少失稳传播数据，本研究暂无法应用。但在区域尺度慢速滑坡场景下，仍可结合神经网络反演岩土参数，再基于有限元法求解应力变形问题（Moeineddin et al., 2023）。

滑坡过程由多个地球系统过程耦合驱动，数据驱动方法通常难以顺序或同步模拟这些过程（Fan et al., 2019）。其中，级联灾害过程（cascading hazard process）尤为关键，涉及多种潜在物理机制对坡体失稳的影响。该问题多通过物理模型方法求解（van den Bout et al., 2021；Pudasaini 和 Krautblatter, 2021），但同样存在前述局限，因此未来可尝试多过程物理模型耦合，实现更逼真的级联滑坡灾害模拟。

本研究面临的另一局限是地震动数据来源于经验公式（Wald et al., 2022），所采用的永久变形模型本身也具备经验性质（Jibson, 2007）。虽然这便于近实时建模，因为主震发生后一小时内可获取首批地震动估算，但若能利用完整地震动波形模拟，可更充分遵循 Newmark (1965) 方法，在区域尺度内提升建模精度（Dahal et al., 2023）。此类模型结构需由简单人工神经网络向更复杂的循环神经网络（Medsker et al., 2001）或 Transformer 模型（Jaderberg et al., 2015）拓展。

6. 结论性评述

物理信息建模方法（Physics-informed modelling approaches）代表了系统科学领域未来科学建模的发展方向。此类方法兼具数据驱动与物理机制约束两方面的优势，具备良好的鲁棒性与应用潜力。在滑坡灾害科学中，数据驱动方法和物理基础方法分别主导了区域尺度与局地尺度的灾害评估，两者各自侧重且互为补充。将两者有机结合，优势互补，可为滑坡易发性与危险性建模提供一种有效的替代路径。

本研究提出的建模框架将永久变形（permanent deformation）分析方法融入深度学习架构之中。该方法通过潜变量（latent variables）学习地质力学参数，并据此估算受物理机制约束的滑坡发生概率。研究结果表明，模型估算得到的地质力学参数值处于可观测且合理的取值范围内，并允许其在空间上呈现差异。这一特性在确保物理可解释性的同时，亦带来了优异的模型预测性能。

在未来应用前景方面，该框架可进一步扩展应用于准实时（near-real-time）预测系统。尽管当前模型中纳入的物理约束能够较好地拟合观测数据并展示出良好的应用潜力，但若能在滑坡启动阶段进一步引入应力-变形（stress–deformation）分析方法，将有助于模型性能的提升。实现这一目标需依赖具备中间变形量观测以及应力–应变条件记录的高质量滑坡灾害目录。此外，本研究还可通过引入多物理过程（multi-physical earth system process）对地球系统耦合过程的建模，进一步提升滑坡易发性预测模型的通用性与物理一致性。

致谢

本研究使用了荷兰国家电子基础设施，获得SURF Cooperative机构提供的No. EINF-7984号资助。同时，作者感谢沙特阿卜杜拉国王科技大学（KAUST）竞争性科研资助计划对本研究提供资金支持（项目编号：URF/1/4338-01-01）。

附录 A. 补充数据

本研究相关补充材料可通过以下链接在线获取：
https://doi.org/10.1016/j.enggeo.2024.107852

数据可用性声明

为促进实验结果的复现性和可重复性，本文相关数据与代码已在以下GitHub仓库中公开共享：
https://github.com/ashokdahal/PINN.git