二分查找有三种
[0,n-1] <= +-1更新
[0,n-1) < r=
(-1,n) l+1<r l / r=
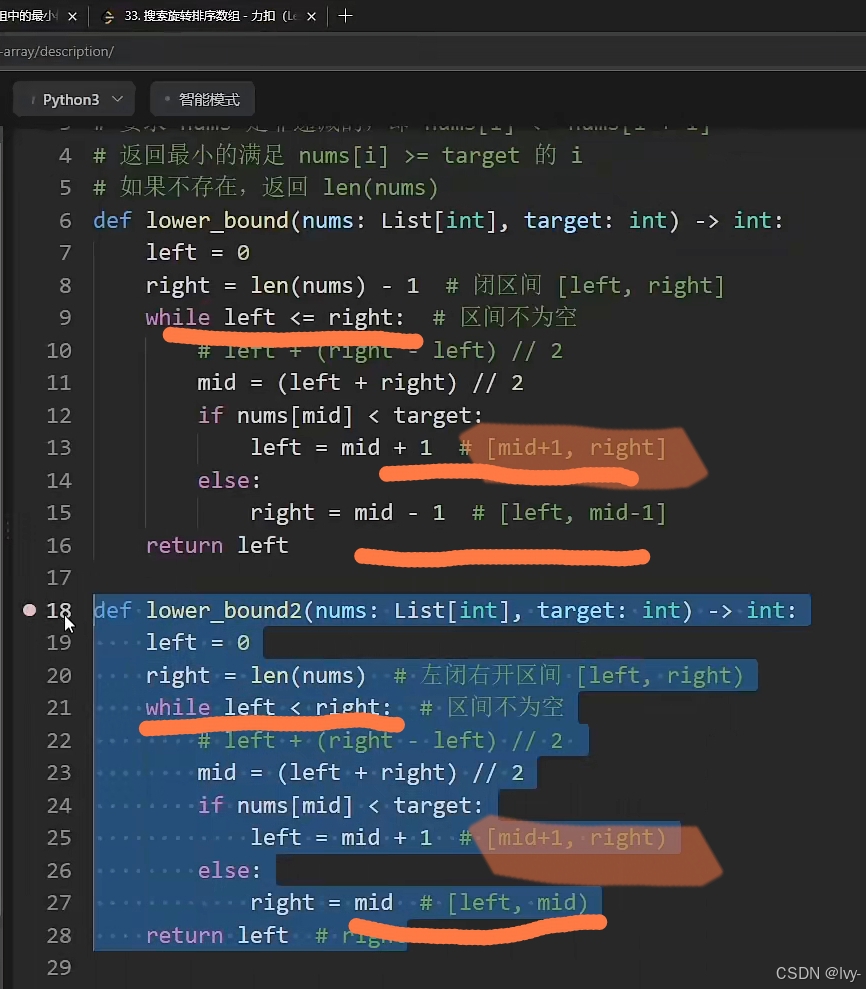

闭区间,找数组上下界
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target)
{
int l=0,n=nums.size();
if(n==0 || nums[n-1]<target)
return {-1,-1};
int r=n-1;
while(l<=r)
{
int mid=l+(r-l)/2;
if(nums[mid]<target)
l=mid+1;
else
r=mid-1;
}
if(nums[l]!=target) return {-1,-1};
int low=l;
l=0;
r=n-1;
while(l<=r)
{
int mid=l+(r-l)/2;
if(nums[mid]<=target)
l=mid+1;
else
r=mid-1;
}
int up=r;
return {low,up};
}
};
寻找峰值
左闭右开,return l
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int n = nums.size();
if (n == 1) return 0;
int l = 0, r = n - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] > nums[mid + 1]) {
r = mid; // 峰值在左半部分
} else {
l = mid + 1; // 峰值在右半部分
}
}
return l; // 最终l=r,指向峰值位置
}
};
闭区间,旋转数组最小值,和最后一个数比较
class Solution {
public:
int findMin(vector<int>& nums)
{
int n=nums.size();
int l=0,r=n-1;
while(l<=r)
{
int mid=l+(r-l)/2;
if(nums[mid]>nums[n-1])
l=mid+1;
else
r=mid-1;
}
return nums[l];
}
};
lc33.两次二分
1.二分找旋转点
2.判断所在区间
3.区间二分找tar
但下面代码对处理n=2存在漏洞,待解决
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
if (n == 0) return -1;
// 第一步:找到旋转点(数组开始递增的位置)
int l = 0, r = n - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] < nums[n - 1]) {
r = mid; // 旋转点在左半部分
} else {
l = mid + 1; // 旋转点在右半部分
}
}
int rotatePos = l; // 旋转点位置
// 第二步:根据旋转点确定二分搜索范围
if (target >= nums[0]) {
// 目标值在非旋转的前半部分
l = 0; r = rotatePos;
} else {
// 目标值在旋转的后半部分
l = rotatePos; r = n - 1;
}
// 第三步:在确定的范围内二分搜索目标值
while (l <= r) {
int mid = l + (r - l) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return -1; // 目标值不存在
}
};
二分查找_求处理后的最小的最大值
猜数字游戏
class Solution {
public:
int minimumSize(vector<int>& nums, int maxOperations) {
auto check = [&](int m) -> bool {
long long cnt = 0;
for (int x : nums) {
cnt += (x - 1) / m;
}
return cnt <= maxOperations;
};
int left = 0;
int right = ranges::max(nums);
while (left + 1 < right) {
int mid = left + (right - left) / 2;
(check(mid) ? right : left) = mid;
}
return right;
}
}
「二分查找」求「处理后数组的最大值的最小值」,核心逻辑像猜数字游戏
1. 问题场景
假设你有一堆数(比如[3,6,7]),每次操作可以把一个数x分成多个数,但每个数至少为1。比如7可以分成3+4(最大值4),或2+2+3(最大值3)。现在最多能操作maxOperations次,求处理后数组的最大值的最小可能值。
2. 核心思路:二分猜答案
- 我们要猜一个「目标最大值m」,然后验证:用不超过maxOperations次操作,能否让所有数处理后都≤m。
- 如果能,说明m可能还能更小;如果不能,说明m需要更大。
3. 关键函数check(m)
判断「用m作为最大值时,需要多少次操作」:
- 对每个数x,计算需要切多少次才能让每段≤m。公式是 (x-1)/m 。
比如x=7,m=3:
- (7-1)/3 = 2次操作,切成3+3+1(最大值3),确实切2次。
原理:x除以m的商向下取整,(x-1)/m等价于(x+m-1)//m -1,即最少切分次数。
- 所有数的操作次数总和≤maxOperations时,说明m可行。
4. 二分查找过程
- 左边界left:初始设为0(此时check(0)一定不成立,因为数不能≤0)。
- 右边界right:初始为数组最大值(此时每个数不切分,操作次数0,check一定成立)。
- 循环条件 left+1 < right :每次取中间值mid,根据check结果调整边界:
- 如果check(mid)成立(操作次数足够),说明m可以更小,让right=mid;
- 否则,需要增大m,让left=mid。
- 循环结束后,right就是满足条件的最小m。
举个例子
数组nums=[3,6,7],maxOperations=2:
1. right=7(数组最大值),left=0
2. 第一次mid=(0+7)/2=3:
- 计算操作次数:
(3-1)/3=0,(6-1)/3=1,(7-1)/3=2 → 总和0+1+2=3>2,check(3)不成立 → left=3
3. 第二次mid=(3+7)/2=5:
- 操作次数:
(3-1)/5=0,(6-1)/5=1,(7-1)/5=1 → 总和0+1+1=2≤2,check(5)成立 → right=5
4. 此时left+1=4 < right=5,循环继续:
mid=(3+5)/2=4:
- 操作次数:
(3-1)/4=0,(6-1)/4=1,(7-1)/4=1 → 总和0+1+1=2≤2,check(4)成立 → right=4
5. 现在left=3,right=4,left+1不小于right,循环结束,返回right=4。
验证:用4作为最大值时,操作次数刚好2次:
- 6→2+4(切1次),7→3+4(切1次),3不切,最终数组[3,2,4,3,4],最大值4,符合要求。
二分查找

class Solution {
public:
int findDuplicate(vector<int>& nums) {
int min = 1; // 所查找数字范围的最小值
int max = nums.size(); // 所查找数字范围的最大值
while (min < max) {
int mid = (min + max) / 2;
// 计数
int cnt = 0;
for (int v : nums) {
if (v >= min && v <= mid) {
cnt++;
}
}
if (cnt > mid - min + 1) // 个数超出范围长度,即存在重复数
max = mid;
else
min = mid + 1;
}
return min;
}
};
有序链表转二叉搜索树
快慢指针➕前序处理
每一步要记得断开链表

class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
// 如果链表为空,返回空节点
if (!head) return nullptr;
// 只有一个节点时,直接返回这个节点作为根
if (!head->next) {
return new TreeNode(head->val);
}
// 快慢指针找中间节点
ListNode* slow = head;
ListNode* fast = head;
ListNode* prev = nullptr; // 记录 slow 前面的节点
while (fast && fast->next) {
prev = slow;
slow = slow->next;
fast = fast->next->next;
}
// 创建当前根节点
TreeNode* root = new TreeNode(slow->val);
// 断开链表,分成左右两部分
prev->next = nullptr;
// 递归构建左右子树
root->left = sortedListToBST(head); // 左边
root->right = sortedListToBST(slow->next); // 右边
return root;
}
};
二分查找

代码
class Solution {
public:
int maximumTastiness(vector<int>& price, int k) {
sort(price.begin(), price.end());
int n = price.size();
int l = -1, r = (price.back() - price[0]) / (k - 1) + 1, m;
while(l + 1 < r) {
m = l + (r - l) / 2;
int ret = 1, x = price[0];
for(int i = 1; i < n; i++) {
if(price[i] - x >= m) {
ret++;
x = price[i];
}
}
if(ret >= k) l = m;
else r = m;
}
return l;
}
};
这段代码是在解决“最大美味值”问题,核心思路是用「二分查找」找最大间隔,通俗解释如下:
1. 先排序价格
sort(price.begin(), price.end());
把价格从小到大排好序,比如价格数组是[1,3,5,7],排序后方便找规律。
2. 确定二分查找的范围
- l = -1 (左边界,初始设为-1)
- r = (price最后一个 - 第一个)/(k-1) + 1 (右边界)
这里的逻辑是:假设选k个价格,最小间隔的最大可能值不会超过 (最大值-最小值)/(k-1) ,比如选3个数,最大间隔理论上是 (7-1)/(3-1)=3 ,+1是为了包含边界情况。
3. 二分查找过程
循环条件 l + 1 < r :每次取中间值 m ,判断是否能选出k个价格,每个价格之间的间隔至少为 m 。
- 初始化 ret=1 (至少选第一个价格), x=price[0] (第一个价格)
- 遍历数组:如果当前价格减前一个选中的价格≥m,就选这个价格( ret++ ),并更新前一个价格为当前价格。
- 如果能选出≥k个价格( ret>=k ),说明m可以更大,左边界移到m;否则,右边界移到m。
4. 最终结果
循环结束后, l 就是满足条件的最大间隔,即最大美味值。
举个例子
比如价格数组是[1,2,3,4,5],k=3:
- 排序后还是[1,2,3,4,5]
- 右边界r=(5-1)/(3-1)+1=3
- 第一次m=( -1+3 )/2=1:检查能否选3个间隔≥1的价格,显然可以(1,2,3),所以l=1
- 第二次m=(1+3)/2=2:检查能否选3个间隔≥2的价格(1,3,5),可以,l=2
- 第三次m=(2+3)/2=2.5(取整2),此时l+1=3等于r,循环结束,返回l=2。
所以最大美味值是2,即选3个价格,最小间隔为2。