数据结构与算法学习（一）

1 字典树（前缀树）

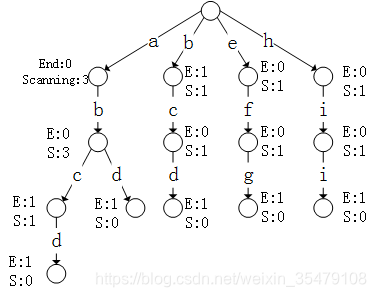
前缀树是N叉树的一种特殊形式。通常来说，一个前缀树是用来存储字符串的。前缀树的每一个节点代表一个字符串（前缀）。每一个节点会有多个子节点，通往不同子节点的路径上有着不同的字符。子节点代表的字符串是由节点本身的原始字符串，以及通往该子节点路径上所有的字符组成的。

对于前缀树，根节点不包含信息，路径保持字符，结点存两个值：pass 和 end。

1. Trie() 初始化前缀树对象
2. void insert(string word) 将字符串word插入前缀树之中
3. int search(string word) 返回前缀树中字符串word的实例个数
4. int prefixNumber(string prefix) 返回前缀树中以prefix为前缀的字符串个数
5. void delete(string word) 从前缀树中移出字符串word

(1) 从类的角度进行描述和实现（哈希）

数据结构的实现，采用struct来构建Trie的节点

// 字典树节点结构
    struct TrieNode {
        int pass;       // 有多少个单词经过此节点
        int end;        // 有多少个单词以此节点结尾
        std::unordered_map<char, TrieNode*> nexts; // 子节点映射表
        TrieNode() : pass(0), end(0) {}
        ~TrieNode() {
            // 递归删除所有子节点，防止内存泄漏
            for (auto& pair : nexts) {
                delete pair.second;
            }
        }
    };
    TrieNode* root; // 根节点

将字符串word插入前缀树之中

void insert(const std::string& word) {
	if (word.empty()) return;
	 TrieNode* node = root;
	 node->pass++;
	 for (char c : word) {
	     if (node->nexts.find(c) == node->nexts.end()) {
	         node->nexts[c] = new TrieNode();
	     }
	     node = node->nexts[c];
	     node->pass++;
	 }
	 node->end++;
}

搜索字符串在树中出现的次数

int countWordsEqualTo(const std::string& word) const {
    const TrieNode* node = root;
    // 利用哈希表来寻找下一个节点
    for (char c : word) {
        auto it = node->nexts.find(c);
        if (it == node->nexts.end()) {
            return 0;
        }
        node = it->second;
    }
    return node->end;
}

返回前缀树中以prefix为前缀的字符串个数

int countWordsStartingWith(const std::string& prefix) const {
    const TrieNode* node = root;
    for (char c : prefix) {
        auto it = node->nexts.find(c);
        if (it == node->nexts.end()) {
            return 0;
        }
        node = it->second;
    }
    return node->pass;
}

从前缀树中删除指定单词

void erase(const std::string& word) {
    if (word.empty() || countWordsEqualTo(word) == 0) return;
    TrieNode* node = root;
    node->pass--; // root中的pass表示有多少个word
    for (char c : word) {
        TrieNode* next = node->nexts[c];
        if (--next->pass == 0) {
            // 递归删除子树
            delete next;
            node->nexts.erase(c);
            return;
        }
        node = next;
    }
    node->end--;
}

最终代码实现

#include <string>
#include <unordered_map>

class Trie {
private:
    // 字典树节点结构
    struct TrieNode {
        int pass;       // 有多少个单词经过此节点
        int end;        // 有多少个单词以此节点结尾
        std::unordered_map<char, TrieNode*> nexts; // 子节点映射表

        TrieNode() : pass(0), end(0) {}
        ~TrieNode() {
            // 递归删除所有子节点，防止内存泄漏
            for (auto& pair : nexts) {
                delete pair.second;
            }
        }
    };

    TrieNode* root; // 根节点

public:
    // 构造函数
    Trie() : root(new TrieNode()) {}

    // 析构函数
    ~Trie() {
        delete root;
    }

    // 插入单词到字典树
    void insert(const std::string& word) {
        if (word.empty()) return;
        
        TrieNode* node = root;
        node->pass++;
        
        for (char c : word) {
            if (node->nexts.find(c) == node->nexts.end()) {
                node->nexts[c] = new TrieNode();
            }
            node = node->nexts[c];
            node->pass++;
        }
        node->end++;
    }

    // 从字典树中删除单词
    void erase(const std::string& word) {
        if (word.empty() || countWordsEqualTo(word) == 0) return;
        
        TrieNode* node = root;
        node->pass--;
        
        for (char c : word) {
            TrieNode* next = node->nexts[c];
            if (--next->pass == 0) {
                // 递归删除子树
                delete next;
                node->nexts.erase(c);
                return;
            }
            node = next;
        }
        node->end--;
    }

    // 统计完全匹配的单词数量
    int countWordsEqualTo(const std::string& word) const {
        const TrieNode* node = root;
        
        for (char c : word) {
            auto it = node->nexts.find(c);
            if (it == node->nexts.end()) {
                return 0;
            }
            node = it->second;
        }
        return node->end;
    }

    // 统计以prefix为前缀的单词数量
    int countWordsStartingWith(const std::string& prefix) const {
        const TrieNode* node = root;
        
        for (char c : prefix) {
            auto it = node->nexts.find(c);
            if (it == node->nexts.end()) {
                return 0;
            }
            node = it->second;
        }
        return node->pass;
    }
};

2 从数组的角度进行实现

#include <string>
#include <cstring>

class Trie {
private:
    static const int MAXN = 150001; // 最大节点数，可根据数据量调整
    int tree[MAXN][26];             // 存储子节点的索引
    int end[MAXN];                  // 标记该节点是否为单词结尾
    int pass[MAXN];                 // 记录经过该节点的单词数量
    int cnt;                        // 当前使用的节点数量

public:
    // 初始化字典树
    Trie() {
        build();
    }

    // 重置字典树
    void build() {
        cnt = 1;
        memset(tree, 0, sizeof(tree));
        memset(end, 0, sizeof(end));
        memset(pass, 0, sizeof(pass));
    }

    // 插入单词到字典树
    void insert(const std::string& word) {
        if (word.empty()) return;
        
        int cur = 1; // 从根节点开始(索引1)
        pass[cur]++; // 根节点pass值增加
        
        for (char c : word) {
            int path = c - 'a'; // 计算字符对应的路径索引(0-25)
            if (tree[cur][path] == 0) {
                tree[cur][path] = ++cnt; // 分配新节点
            }
            cur = tree[cur][path];
            pass[cur]++; // 经过当前节点的单词数+1
        }
        end[cur]++; // 单词结尾标记+1
    }

    // 统计完全匹配的单词数量
    int search(const std::string& word) const {
        if (word.empty()) return 0;
        
        int cur = 1;
        for (char c : word) {
            int path = c - 'a';
            if (tree[cur][path] == 0) {
                return 0; // 路径不存在，单词不存在
            }
            cur = tree[cur][path];
        }
        return end[cur]; // 返回单词结尾标记值
    }

    // 统计以prefix为前缀的单词数量
    int prefixNumber(const std::string& prefix) const {
        if (prefix.empty()) return 0;
        
        int cur = 1;
        for (char c : prefix) {
            int path = c - 'a';
            if (tree[cur][path] == 0) {
                return 0; // 前缀路径不存在
            }
            cur = tree[cur][path];
        }
        return pass[cur]; // 返回经过该节点的单词数
    }

    // 从字典树中删除单词
    void deleteWord(const std::string& word) {
        if (word.empty() || search(word) == 0) return;
        
        int cur = 1;
        pass[cur]--; // 根节点pass值减1
        
        for (char c : word) {
            int path = c - 'a';
            int next = tree[cur][path];
            if (--pass[next] == 0) {
                tree[cur][path] = 0; // 移除路径
                return; // 子树已删除，直接返回
            }
            cur = next;
        }
        end[cur]--; // 单词结尾标记减1
    }

    // 清空字典树
    void clear() {
        for (int i = 1; i <= cnt; i++) {
            memset(tree[i], 0, sizeof(tree[i]));
            end[i] = 0;
            pass[i] = 0;
        }
        cnt = 1;
    }
};

数组中两个数的最大异或值

1. 指针类型的Trie解决

struct Trie{
    // 只包含0和1两个数，因此只需要两个左右指针
    Trie* left = nullptr;
    Trie* right = nullptr;
    Trie() {}
};

class Solution {
private:
    Trie* root = new Trie();
    static constexpr int HIGH_BIT = 30;

public:
    void insert(int num){
        Trie* cur = root;
        for(int k = HIGH_BIT; k >= 0; k--){
            int bit = (num >> k) & 1; //保存第k位的值
            if(bit == 0){
                if(!cur -> left){
                    cur -> left = new Trie();
                }
                cur = cur -> left; //此时指向左边
            }
            else{
                if(!cur -> right){
                    cur -> right = new Trie();
                }
                cur = cur -> right;
            }
        }
    }

    int MaxXor(int num){
        Trie* cur = root;
        int x = 0;
        for(int k = HIGH_BIT; k >= 0; k--){
            int bit = (num >> k) & 1;
            if(bit == 0){
                //此时希望异或最大，去寻找包含1的右节点
                if(cur -> right){
                    cur = cur -> right;
                    x = (x << 1) + 1;
                }
                else{
                    cur = cur -> left;
                    x = x << 1;
                }
            }
            else{
                if(cur -> left){
                    cur = cur -> left;
                    x = (x << 1) + 1;
                }
                else{
                    cur = cur -> right;
                    x = x << 1;
                }
            }
        }
        return x;
    }

    int findMaximumXOR(vector<int>& nums) {
        int x = 0;
        for(int i = 1; i < nums.size(); i++){
            insert(nums[i-1]);
            x = max(x, MaxXor(nums[i]));
        }
        return x;
    }
};

2. 数组类型的Trie解决