【CF】⭐Day104——Codeforces Round 840 (Div. 2) CE (思维 + 分类讨论 | 思维 + 图论 + DP)

C. Another Array Problem

题目：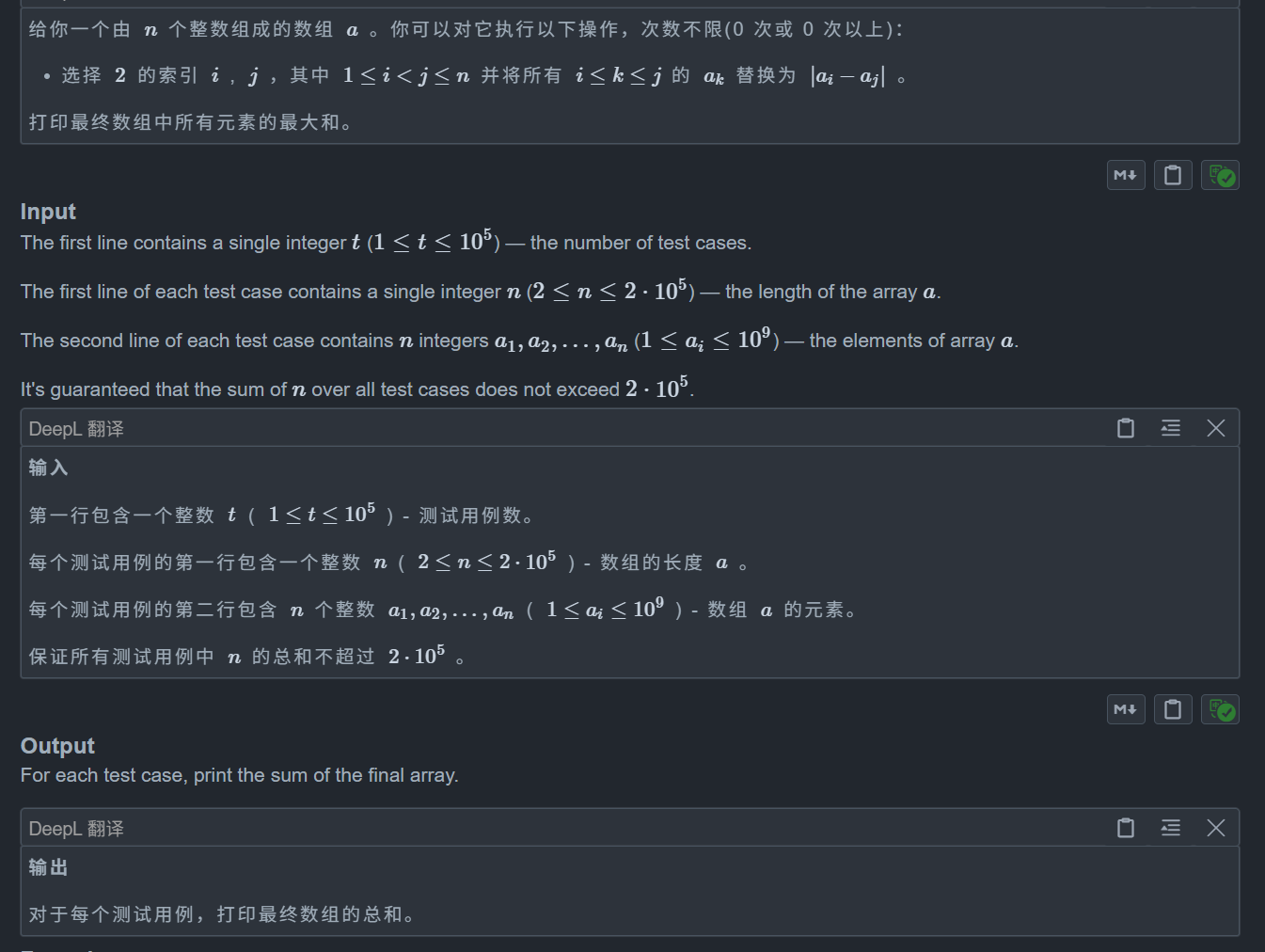

思路：

纯思维题，但是理解错题意

我们题目中说可以执行任意次操作，那么我们如果对同一个地方执行两次操作呢？

显然这一块都将变成 0，那么我们就能执行最优操作了

我们分类讨论一下：

①. n >= 4

此时我们无论最大值 mx 处于哪里，我们都能将所有值变为 mx，如果处于中间，那么就直接将两边全变为 0，然后再变成 mx 即可，如果处于端点，那么也是一样的操作，如果处于次边缘（如第二个），那么就要有点细节了，先把一边全变成 mx，然后再把第一个和第二个变成 0，最后再变成 mx

②. n == 2

此时暴力枚举即可，一个是不改变即 a0 + a1，一个是变成 2 * abs(a0 - a1) 

③. n == 3

此时有些细节，首先肯定是有不改变这个操作，即 a0 + a1 + a2

然后根据 mx 的位置再次讨论，如果 mx 处于两边，那么显然可以变成 3 * a0 或 3 * a2

如果处于中间呢？那么我们肯定是将 a1 与左右两边的试图合并一下，即有 abs(a0 - a1) 或 abs(a1 - a2)，那么对于这个值我们同样也可以全变成他，即变成 3 * abs(***) 

最后我们将所有结果取 max 即可

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
#include <complex>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"

void solve()
{
    int n;
    cin >> n;
    vector<int> a(n,0);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    if (n == 2)
        cout << max({ 2 * abs(a[0] - a[1]), a[0] + a[1] });
    else if (n == 3)
        cout << max({ 3 * (abs(a[0] - a[1])), 3 * (abs(a[2] - a[1])), 3 * a[0], 3 * a[2], a[0] + a[1] + a[2] });
    else
    {
        int mx = 0;
        for (auto i : a)
            mx = max(i, mx);
        cout << n * mx;
    }
    cout << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

E. Node Pairs

题目：

思路：

感觉遇到相互到达什么的就应该往联通上想

首先题目让我最小化节点数，那么根据题目中的定义，一个大小为 s 的强连通分量的奉献就是 s * (s - 1) / 2，因为其中的点两两互达

所以我们可以做一个完全背包，具体实现在代码中

对于第二问要让我们单项节点对数最大，那么对于所有节点来说任意两点都有一条边是最优的，即有 tot * (tot - 1) 条边，但是由于其中 p 条都是双向的，以此还需要减去 p

具体如何构造呢？我们直接将强连通分量缩点，然后对于每两个点之间就是 size_a * sizeb_b 个单项边了

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
#include <complex>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"

void solve()
{
    int p;
    cin >> p;
    //dp[i] 代表 含有 i 对节点时的最少节点数
    vector<int> dp(p+1, 1e18);
    dp[0] = 0;
    //完全背包，枚举 节点对数 i
    for (int i = 1; i <= p; ++i)
    {
        //枚举强联通分量大小，大小为 s 的强联通分量能产生 s * (s - 1) / 2 个节点对，其含有的节点数为 s
        for (int s = 1; (s * (s - 1)) / 2 <= i; ++s)
        {
            dp[i] = min(dp[i], dp[i - (s * (s - 1)) / 2] + s);
        }
    }
    //对于所有节点我们能构造出 cnt * (cnt - 1) / 2 个点对，其中 p 个是双向的，而我们恰好能构造出 tot - p 的图
    cout << dp[p] << " " << dp[p] * (dp[p] - 1) / 2 - p << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    while (t--)
    {
        solve();
    }
    return 0;
}