文章目录
前言
感觉前四道,就是考对于题目的理解能力,以及自己的模拟能力
A.Only One Digit
题目传送门:Only One Digit



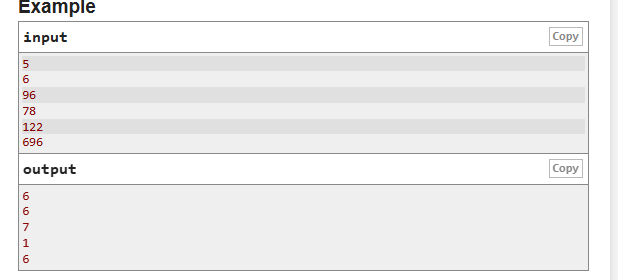

对于这一题,只要读懂题之后,一个排序就行了
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
void solve()
{
string s;
cin>>s;
ll n[5];
for(ll i=0;i<s.size();i++)
{
n[i]=s[i]-'0';
}
sort(n,n+s.size());
cout<<n[0]<<endl;
}
signed main()
{
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
B.No Casino in the Mountains
题目传送门:No Casino in the Mountains


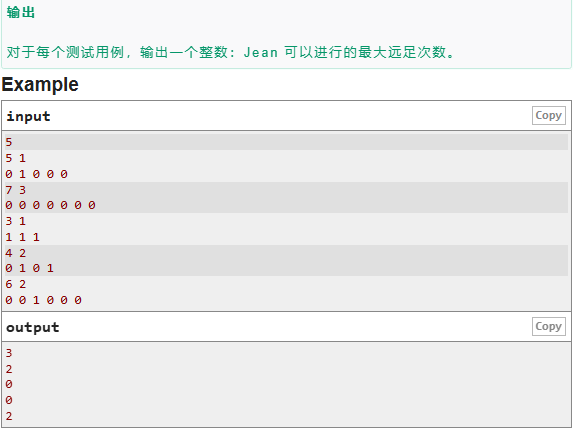

这一题由于只有0和1,故就想到了前缀和,然后再按照题目描写的模拟一下就行了
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll s[N];
ll a[N];
void solve()
{
ll n,k;
cin>>n>>k;
ll sum=0;
ll ans=0;
for(ll i=1;i<=n;i++)
{
cin>>s[i];
a[i]=a[i-1]+s[i];
if(s[i]==1)
sum++;
}
if(sum==n)//特判一下是否全为1
{
cout<<0<<endl;
return ;
}
ll x=0;
for(ll i=1;i<=n;i++)
{
x=i;
if(s[i]==0)//为了去除开头连续的1
break;
}
for(ll i=x;i+k-1<=n;i++)
{
if(a[i+k-1]-a[i]==0&&s[i]==0)//判断一下是否满足条件
{
ans++;
i=i+k;
}
}
cout<<ans<<endl;
}
signed main()
{
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
C. I Will Definitely Make It
题目传送门:I Will Definitely Make It
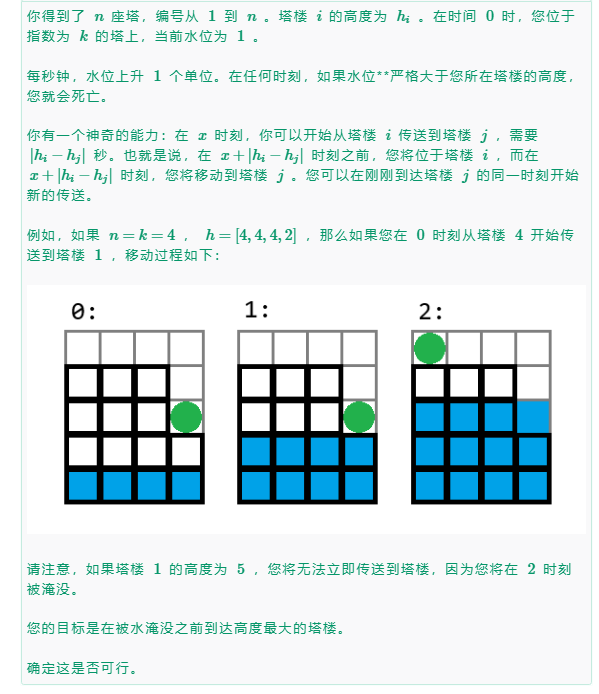

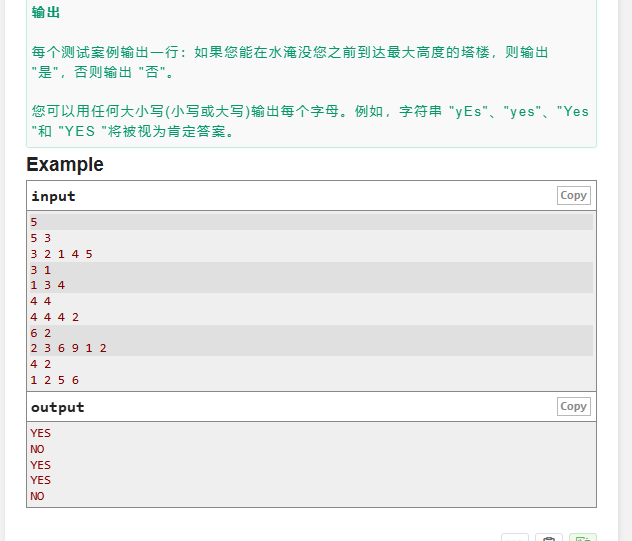

对于这一题当时快写吐了,等到快结束的时候,又重新读了一下题,才发现之前理解错了,导致一直过不了,最后剩几分钟,也来不及改了,结束之后,重新敲了一遍,直接过了,无语。
主要思路:
通过观察会发现当开始在哪座山时,只要之后的山与当前的位置高度小于等于,最开始山的高度,就不会被淹,只需要排完序之后,来进行判断从最开始的山一直到最高的山是否,会出现高度差大于最开始山的高度。如果出现了就是“NO”,否则就是“YES”;
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll s[N];
ll s1[N];
void solve()
{
ll n,k;
cin>>n>>k;
for(ll i=1;i<=n;i++)
{
cin>>s[i];
}
ll a=s[k],x=0;;
sort(s+1,s+n+1);
for(ll i=1;i<=n;i++)
if(s[i]==a)
x=i;
ll m=1;
for(ll i=x;i+1<=n;i++)
{
s1[m++]=s[i+1]-s[i];//将高度差存入数组中
}
sort(s1+1,s1+m);//对其进行排序
ll f=0;
for(ll i=1;i<m;i++)
{
if(s1[i]>a)//如果出现大于起始高度时就进行标记,如何跳出循环
{
f=1;
break;
}
}
if(f)
cout<<"NO"<<endl;
else
cout<<"YES"<<endl;
}
signed main()
{
IOS;
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
D.This Is the Last Time
题目传送门:This Is the Last Time


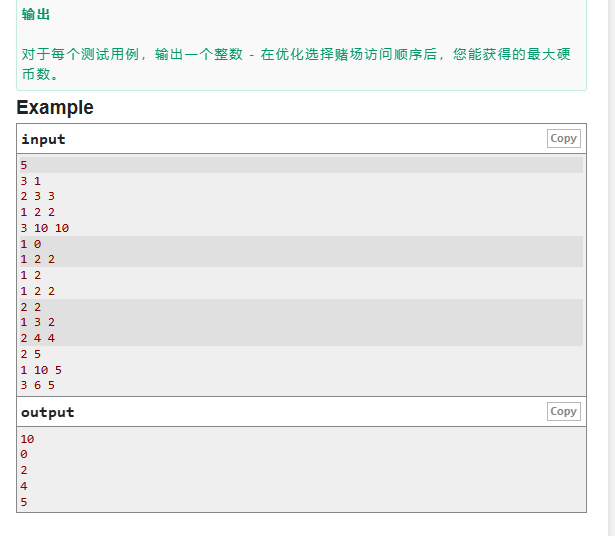

这一题就是贪心,当时只想着就进行排序,然后对其答案进行更新,没有约束最大值,导致wa了两发,然后改了过来,由于数组开小了,又wa了1发。WA警示自己!!!
解题思路:
这一题只需要利用结构体按照L从小到大排序,然后循环,最后再循环的时候约束一下最大值就行了。
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e5+10;
struct node{
ll x,y,sum;
}s[N];
bool cmd(node a,node b)
{
return a.x<b.x;
}
void solve()
{
ll n,k;
cin>>n>>k;
for(ll i=1;i<=n;i++)
{
cin>>s[i].x>>s[i].y>>s[i].sum;
}
sort(s+1,s+1+n,cmd);//按照x从小到大排序
ll ans=k;
for(ll i=1;i<=n;i++)
{
if(ans>=s[i].x&&ans<=s[i].y&&ans<=s[i].sum)//如果大于sum,则进行更新,
ans=s[i].sum;
}
cout<<ans<<endl;
}
signed main()
{
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
E.G-C-D, Unlucky!
题目传送门:E.G-C-D, Unlucky!


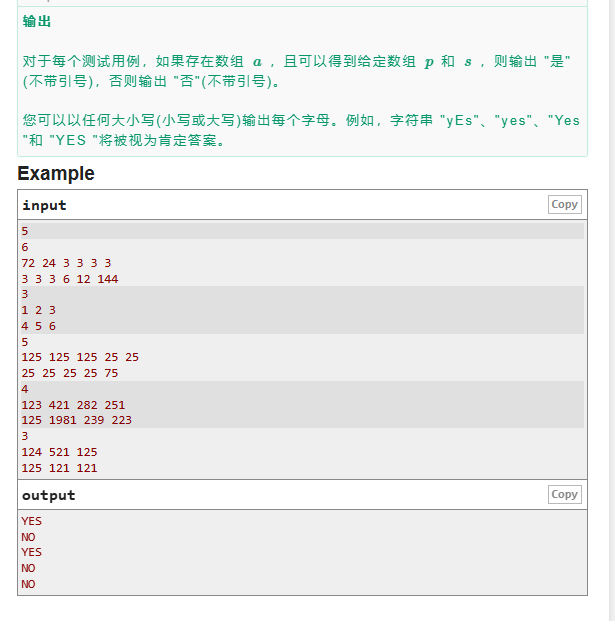

解题思路:
这一题就是找规律题,
1. 通过前缀与后缀的定义就会发现,前缀与后缀数组,到最后都是包含了所有数;故前缀数组的最后一个数与后缀数组的第一个数应该相同。
2. 由于公约数是求两个数的公因数,而公因数都是小于等于这这两个数最小的本身,由此可以得到,其数组必定是单调的
前缀: 非单调递增。
后缀:非单调递减。
3. 就是公约数的性质了


AC代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll a[N],b[N],c[N];
ll lcm(ll x,ll y)
{
return x*y/__gcd(x,y);
}
void solve()
{
ll n;
cin>>n;
for(ll i=1;i<=n;i++)
cin>>a[i];
for(ll i=1;i<=n;i++)
cin>>b[i];
if(a[n]!=b[1])
{
cout<<"NO"<<endl;
return ;
}
for(ll i=1;i+1<=n;i++)
{
if(a[i]<a[i+1])
{
cout<<"NO"<<endl;
return ;
}
}
for(ll i=1;i+1<=n;i++)
{
if(b[i]>b[i+1])
{
cout<<"NO"<<endl;
return ;
}
}
for(ll i=1;i<=n;i++)
{
ll l=lcm(a[i],b[i]);
if(i>1&&__gcd(a[i-1],l)!=a[i])
{
cout<<"NO"<<endl;
return;
}
if(i+1<=n&&__gcd(b[i+1],l)!=b[i])
{
cout<<"NO"<<endl;
return;
}
}
cout<<"YES"<<endl;
}
signed main()
{
IOS;
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
lcm(a[i],b[i])
a[i]=p[i];
b[i]=s[i];
如果从传递性来进行推理的话
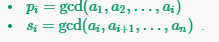
lcm求出来的就是a[i]然后再利用传递性与p[i-1]求最大公因数
构造的核心思想:
对于每个位置 i,构造候选的数组 a 元素为 a[i](前缀 GCD)和 b[i](后缀 GCD)的最小公倍数 l。因为 a 数组的元素需要同时是前缀 GCD 和后缀 GCD 的倍数,最小公倍数是满足该条件的最小可能值 。
总结
不知道是在协会敲代码,敲习惯了,看着大屏幕,很少分神。然而到了寝室看自己的电脑敲代码,总是很难集中注意看题。总是看着题目读着读着心神就飘到其他地方去了~~~~
嗯,集中注意力,下回必须集中注意力!!!