图像分析学习笔记（2）：图像处理基础

图像增强方法

• 目的：改善视觉效果，例如增强对比度
• 定义：为了改善视觉效果、便于人或计算机对图像的分析理解，针对图像的特点或存在的问题，采取的改善方法或加强特征的措施。
• 本质：有选择地加强图像中的某些信息，抑制另一些信息，产生一幅新的图像
• 增强方法的分类：空间与方法，频域方法，混合域方法
• 空间域方法：直方图，回复直方图是灰度的概率密度，横坐标为灰度，纵坐标为每种灰度的像素频率
  • 通常情况下，若一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀，则该图像会有高对比度的外观$\to$直方图均衡化：找到一种变换使得变换后的概率密度函数均匀分布。$$s_k^{\prime }=T(r_k)=\sum _{j=0}^{k}P(r_j)$$
  • 直方图均衡化的实质：占有较少像素的灰度变换后被归并；直方图均衡化的缺点：由于灰度归并，可能损失一些图像细节；处理后的图像显得粗犷。
• 频域方法
  • 二维傅里叶变换
    $$F(u,v)=\frac{1}{MN}\sum _{x=0}^{M-1}\sum _{y=0}^{M-1}f(x,y)exp[-j2\pi (\frac{ux}{M}+\frac{vy}{N})]u=0,1,\dots ,M-1,v=0,1,\dots ,N-1$$
  • 二维傅里叶变换的物理意义：
    类比一维傅里叶变化，二维傅里叶变化的本质在于将图像分解成若干个平面正弦波之和。
  • 二维正弦波的确定需要四个参数：幅值、频率、相位、方向。
  • 高频分量代表图像中的边缘、细节等内容；低频分量代表图像中缓慢变化的内容。
  • 同态滤波：目的：改善图像中偏暗的区域。 模型：建立图像的反射成像模型为：$$f(x,y)=i(x,y)r(x,y)$$
    $i(x,y)$:照度分量，缓慢变化，对应于低频部分；$r(x,y)$:反射分量，快速变化，对应于高频部分。 方法：为增强较暗部分的细节，将图像转到频域，设计频域滤波函数，减弱图像的低频分量，加强高频分量。
• 同态滤波步骤：
  • 根据反射成像模型，有：$f(x,y)=i(x,y)r(x,y)$；
  • 两边取对数：$lnf(x,y)=lni(x,y)+lnr(x,y)$
  • 两边取傅氏变换：$F(u,v)=I(u,v)+R(u,v)$
  • 用同态滤波函数$H(u,v)$处理$F(u,v)$：$$H(u,v)F(u,v)=H(u,v)I(u,v)+H(u,v)R(u,v)$$
  • 两边取反傅氏变换：$f^{\prime }(x,y)=i^{\prime }(x,y)+r^{\prime }(x,y)$
  • 两边取指数：$g(x,y)=exp|f^{\prime }(x,y)|$
• 为什么叫同态滤波？同态系统：通过非线性变换将非线性组合信号变换为线性组合信号，以便于进行线性处理的一类系统的总称。

图像复原方法

• 图像复原的目的：恢复出最接近原始图像的输出图像

• 图像复原的概念

  • 图像退化：图像获取过程可能出现模糊、畸变、噪声，使图像降质的现象。
  • 图像复原：根据退化模型和先验信息，按照某种准则，从退化图像恢复出最接近原始图像的输出图像。
  • 与图像增强的区别：图像复原会用到先验信息。

• 图像退化的原因：

  • 相机与景物之间存在相对运动，造成运动模糊
  • 图像在成像、采集、处理过程中，引入噪声
  • 光学系统的像差、镜头畸变、带宽有限，造成图像失真
  • 相机扫描机构的非线性，引起几何失真
  • 光学系统或探测器特性不均匀，造成相同亮度的景物表现出不同灰度（灰度失真）
  • 传输介质（如大气湍流、大气成分变化）引起辐射失真

• 图像退化和复原的过程建模：

  • $$\begin{gathered} g(x,y)=H[f(x,y)]+n(x,y) \\ f(x,y)=P[g(x,y)] \end{gathered}$$

• 图像去噪：噪声：在成像、数字化、采集和处理过程中产生的；会扰乱图像的可观测信息。噪声的描述与建模：噪声类型由产生噪声的物理过程决定，通常用特定的概率密度函数(PDF)建模。 高斯噪声：高温引起的传感器噪声（热噪声）脉冲噪声：电磁干扰以及通信系统的故障和缺陷（雪花噪声）瑞利噪声。指数噪声。

  • 图像去噪的分类： 空域滤波方法：均值滤波器；统计排序滤波器； 频域滤波方法：带阻滤波器、带通滤波器、陷波滤波器
  • 空域滤波：使用空域模板进行的图像处理。模板又被称为空域滤波器。$$g(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t)$$
  • 均值滤波的作用 减小图像灰度的“尖锐”变化，减小噪声；由于图像边缘是由图像灰度尖锐变化引起的，所以也存在边缘模糊的问题。
  • 统计排序滤波器：以目标像素邻域的像素值排序结果代替中心像素的值。最大值滤波器：用像素领域内的最大值代替该像素（去除胡椒噪声）；最小值滤波器：用像素领域内的最小值代替该像素（去除盐噪声）；中值滤波器：用像素领域内的中间值代替该像素（去除脉冲噪声）

• 退化模型估计：在退化函数H满足线性性、位置不变性的条件下，图像退化过程可以表示为：一个空域滤波器 h(x,y) 在图像 f(x,y) 上的卷积。

  • 图像观察估计：只有退化图像的信息，没有任何关于退化函数的信息。
  • 试验估计：在具有相同的装置，且能够进行重复试验的情况下
  • 建模估计：知道引起图像退化的物理特性/机理，且能够使用数学模型进行表示时可使用该方法。
  • 以运动模糊为例：正常拍照情况下，如果画面是f(x,y)，假设曝光时间为T，则成像g(x,y)的表达式如下：$$g(x,y)={\int }_0^{T}f(x,y)dt=Tf(x,y)$$ 传感器上成的像，是画面在曝光时间下累积在传感器上的能量。

• 逆滤波复原
  

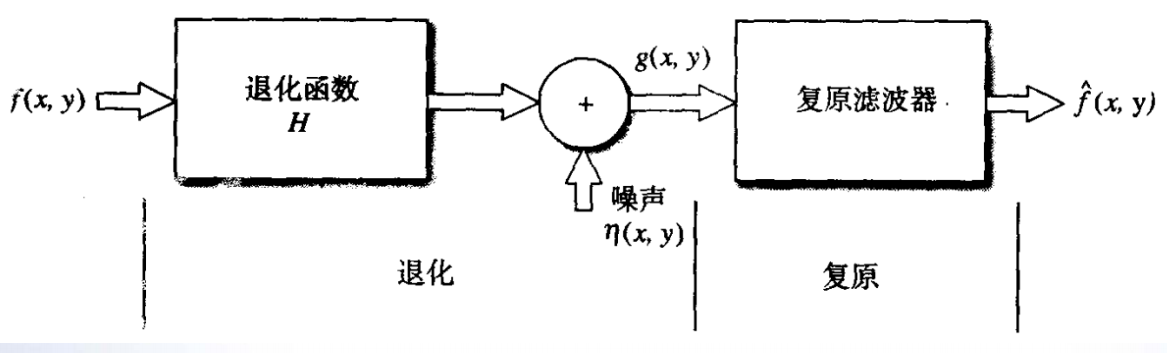
• 维纳滤波复原：使复原图像与原始图像的均方误差最小，即：$$\min ({\epsilon }^2)=\min (E\left\{{\left[f(x,y)-\hat{f}(x,y)\right]}^2\right\})$$

• 维纳滤波 v.s.逆滤波 无噪声时，$S_{nn}(u,v)=0$，维纳滤波即为逆滤波。有噪声时，维纳滤波用噪信功率比对恢复过程进行修正。

图像分割方法

• 图像分割的目的：将目标从背景中分离出来。
• 图像分割与图像语义分割的区别：图像分割的结果不需要提供区域的语义类别信息。
• 根据灰度、颜色、纹理、形状等特征，将图像分成若干个区域｛S1, S2 … Sn｝，让区域间显差异性，区域内呈相似性。
• 正确的区域分割必须满足以下条件：
  • 图像分割的完整性：图像中的像素无一漏网：
  • 区域之间互不相交
  • 同一区域内特征一致
  • 相邻区域特征不一致
  • $$\begin{array}{c}X={\bigcup }_{i=1}^{n}S,\\ S_i\cap S_j=\Phi ,\\ P(S_i)=True,\\ P(S_1\cup S_2)=False\end{array}$$
• 图像分割的输出：一般为二值图像
• 区域：在数字图像中，每个像素周围有8个邻接像素，常见的邻接关系有3种：4邻接、8邻接、混合邻接。若两个像素之间有一条通路能通过邻接关系把它们连接
  起来，那么这两个像素就是连通的。彼此连通的点形成了的集合称为连通区域。
• 图像分割的实质：对图像的特征空间进行划分
• 以灰度特征为例，图像分割的基本思路：①、以寻找区域间的不一致性为出发点 基于边缘的分割方法。②、以寻找区域内的一致性为出发点 基于阈值的分割方法 基于区域的分割方法 基于聚类的分割方法
• 基于边缘的分割方法：边缘意味着一个区域的终结，和另一个区域的开始。
• 基于阈值的分割方法：确定灰度阈值，并将图像中每个像素的灰度值与阈值进行比较，根据比较结果将像素分配到合适的类别中。关键问题在于灰度阈值的确定。单阈值分割：针对图像中只有目标和背景的情况。
  • 单阈值分割：针对图像中只有目标和背景的情况。
  • 确定阈值的三种方法：手动阈值分割；直方图双峰法；自适应阈值图像分割。
    • 直方图双峰法：已知图象仅包含具有明显灰度差别的目标和背景，此时灰度直方图通常为双峰单谷型，取谷底点为阈值即可完成分割。
    • 自适应阈值图像分割：定义一种准则，自动求解阈值，使得分割结果满足上述准则。迭代法和大津法
• 基于区域的分割方法
  • 区域生长：将每个像素与邻域中足够相似的像素连接，完成图像分割。关键：确定生长准则 or 相似性度量。灰度差；相对灰度差（像素间灰度差/邻域标准差）
  • 区域分割与聚合：按照特定的准则将图像分割成一系列任意不相关的区域，然后将它们合并以满足限制条件。
  • 分水岭分割算法：地形图(topographic map)：地表起伏形态和地理位置、形状在水平面上的投影图。 每幅图像都是一幅“地形图”，以图像长宽为x，y轴，以像素亮度为z轴。模拟自底向上逐渐淹没地形过程。当两个山谷的水将要汇合时，在汇合处建立堤坝，直到整个
    地形都被淹没，从而就得到了各个堤坝(分水岭)和一个个被堤坝分开的盆地(目标物体)。
• 基于聚类的分割方法：寻找不同“类别”的中心点
• 拓展：基于图理论的分割方法

形态学处理

• 以形态为基础对图像进行分析。简化图像数据，保持它们基本的形状特性，并除去不相干的结构。
• 形态学处理的数学基础是集合论
• 集合运算：映像、位移
• 形态学处理的基本思想：采用一定形态的结构元素B，去度量和提取图像A中物体的形状。
• 形态学处理的基本运算：膨胀、腐蚀、开操作、闭操作。
  • 膨胀运算定义为集合 $A$ 与结构元素 $B$ 的平移并集：
    A ⊕ B = { z ∣ ( B ^ ) z ∩ A ≠ ∅ } A \oplus B = \{ z | (\hat{B})_z \cap A \neq \emptyset \} A⊕B={z∣(B^)z​∩A=∅}
    其中 $\hat{B}$ 表示 $B$ 的反射（对称集），$(\hat{B}{)}_z$ 表示 $B$ 平移 $z$ 后的集合。
    膨胀的目的是将二值化图像的边界向外扩张，扩张的方式由结构元素
    决定。
  • 腐蚀运算定义为结构元素 $B$ 完全包含在集合 $A$ 中的所有平移点：
    A ⊖ B = { z ∣ B z ⊆ A } A \ominus B = \{ z | B_z \subseteq A \} A⊖B={z∣Bz​⊆A}
    其中 $B_z$ 表示 $B$ 平移 $z$ 后的集合。
    目的：将二值图像中物体的边界向内收缩，使其“腐蚀”。
  • 开操作是先腐蚀后膨胀的复合运算：
    $$A\circ B=(A\ominus B)\oplus B$$
    目的为断开图像中狭窄的连接和消除细的突出物。
  • 闭操作是先膨胀后腐蚀的复合运算：
    $$A\bullet B=(A\oplus B)\ominus B$$
    目的：消除图像中小的孔洞，并填补轮廓线中的断裂。
• 基本运算的应用：边界提取、区域填充、连通分量的提取、细化、粗化
• 形态学应用中，结构元素的形状由具体任务确定
• 形态学可以拓展至灰度图像：二值形态学中用到的和并运算在灰度形态学中分别用最大极值和最小极值运算代替。