作为集成学习的“元老”技术,Bagging(Bootstrap Aggregating) 凭借其简单高效的特点,成为提升模型性能的利器。今天我们就来拆解它的工作原理,并揭秘如何用它和决策树构建强大的随机森林(Random Forest)!
🎯 一、Bagging是什么?为什么需要它?
Bagging = Bootstrap(自助采样) + Aggregating(结果聚合)
想象你有一份原始数据集(比如1000张猫狗图片),直接训练一个决策树模型,可能因数据噪声或模型敏感导致过拟合(训练集表现好,测试集翻车)。
Bagging的解决方案很巧妙:
“与其依赖一个复杂模型,不如训练多个简单模型,让它们投票做决定!”
通过并行训练多个基学习器(如决策树)并汇总结果,显著降低模型方差,提升泛化能力
🔄 二、Bagging工作流程三步曲
1️⃣ Step 1:Bootstrap采样——数据界的“幸运大转盘”
操作:从原始数据集 有放回地随机抽取样本(比如抽1000次)
特点:每个子集大小 = 原始集,但样本可能重复
隐藏福利:约36.8%的样本未被抽中(称为 OOB数据),可当免费验证集
2️⃣ Step 2:训练基学习器——种下多棵“差异化的树”
对每个子集训练一个基学习器(常用决策树)
关键点:树之间要有差异性!
方法1:每棵树用不同数据子集(Bagging核心)
方法2:随机森林中额外限制特征选择(后文详解)
3️⃣ Step 3:结果聚合——民主投票定结果
分类任务:所有树投票,少数服从多数(硬投票)
如:3棵树的预测为 [猫, 狗, 猫] → 最终预测“猫”。
- 回归任务:所有树输出取平均值
如:3棵树预测房价 [100, 105, 102] → 最终预测102.3万
🌱 三、为什么用决策树做Bagging?
决策树是Bagging的“黄金搭档”,因为:
高方差敏感:单棵树容易过拟合,Bagging能有效降低方差
训练效率高:树结构简单,适合并行训练
解释性保留:虽失去单棵树的可解释性,但特征重要性仍可分析
🌲 四、从Bagging到随机森林:双重随机性!
随机森林是Bagging的升级版,核心改进:引入特征随机性!
随机森林=Bagging +决策树
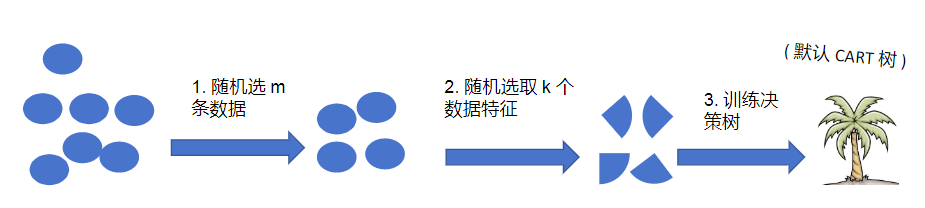
🔍 随机森林工作流程:
样本随机:继承Bagging的Bootstrap采样(每棵树用63.2%的样本)
特征随机:每棵树分裂节点时,随机选部分特征(比如总特征数√d)
训练决策树: 默认 CART 树
重复1-3步构造n个弱决策树
平衡投票集成n个若决策树
⚙️ 为什么需要特征随机?
传统Bagging中,若所有树用相同特征,模型多样性不足
特征随机性进一步降低树之间的相关性,增强抗过拟合能力
🧪 五、实战案例:Python手把手实现随机森林
场景:鸢尾花分类(3种花,4个特征)
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 随机森林参数设置
rf = RandomForestClassifier(
n_estimators=100, # 树的数量
max_features="sqrt", # 每棵树随机选√4=2个特征
max_depth=3, # 控制树复杂度
oob_score=True # 使用OOB数据评估模型
)
rf.fit(X_train, y_train)
# 评估
print("测试集准确率:", rf.score(X_test, y_test))
print("OOB准确率:", rf.oob_score_) # 免交叉验证!🔧 关键参数解释:
n_estimators:树的数量(越多越稳定,但计算量增大)。max_features:每棵树使用的特征数(推荐"sqrt"或"log2")。max_depth:树的最大深度(控制复杂度,防止过拟合)。
📊 输出特征重要性(随机森林的隐藏技能!)
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
# 加载 iris 数据集
iris = load_iris()
X = iris.data # 特征
y = iris.target # 目标变量
# 训练一个随机森林模型(假设 rf 是已经训练好的模型)
# 如果还没有训练模型,需要先训练,例如:
rf = RandomForestClassifier()
rf.fit(X, y)
# 获取特征重要性
features = iris.feature_names # 特征名称
importances = rf.feature_importances_ # 特征重要性
# 可视化
plt.barh(features, importances)
plt.title("特征重要性排序")
plt.xlabel("特征重要性")
plt.show()输出结果:
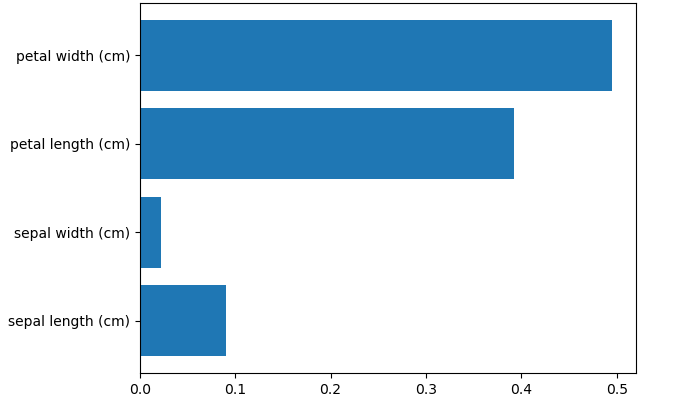
由此可以看到 petal length 和 petal width 的重要性远高于其他特征。
⚖️ 六、Bagging vs 随机森林 vs 其他集成方法
特性 |
Bagging |
随机森林 |
Boosting(如GBDT) |
|---|---|---|---|
样本处理 |
有放回抽样 |
有放回抽样 |
加权错误样本 |
特征处理 |
全特征 |
随机选子特征 |
全特征 |
训练方式 |
并行 |
并行 |
串行 |
核心目标 |
降低方差 |
降低方差+特征鲁棒 |
降低偏差 |
典型基模型 |
任意模型 |
决策树 |
决策树 |
💡 关键区别:随机森林通过特征随机性进一步打破树的相关性,比普通Bagging更鲁棒!
🔍 七、随机森林 vs Bagging决策树:实战对比
| 特性 | Bagging决策树 | 随机森林 |
|---|---|---|
| 样本随机性 | ✅ 有放回采样 | ✅ 有放回采样 |
| 特征随机性 | ❌ 使用所有特征 | ✅ 随机选择特征子集 |
| 过拟合风险 | 中(仅样本随机) | 低(双重随机) |
| 计算成本 | 中(多棵树) | 高(多棵树+特征随机) |
| 适用场景 | 数据量大、特征相关性低 | 数据量大、特征复杂、高维数据 |
💎 八、总结:什么时候用随机森林?
✅ 推荐场景:
数据维度高(如基因数据、文本特征)
存在噪声或缺失值(随机森林对此不敏感)
需要快速基线模型(无需精细调参即有效)
⚠️ 注意事项:
避免用在线性数据(如房价预测),传统回归更合适
树数量
n_estimators建议100~500,过多可能边际效益递减特征随机比例
max_features:分类问题用sqrt(d),回归问题用d/3