论文Review Registration TEASER | TRO | MIT出品，点云配准经典BenchMark | 硬核的数学长文

基本信息

题目：TEASER: Fast and Certifiable Point Cloud  Registration

来源：2021 TRO

学校：MIT

是否开源：https://github.com/MIT-SPARK/TEASER-plusplus

摘要：大量外点情况下的全局点云配准方法

        针对存在大量离群点对应关系的两组三维( 3-D )点的配准，我们提出了第一个快速且可证明的算法。可证明算法是试图解决一个难以解决的优化问题(例如,带有异常值的robust估计)，并提供易于检查的条件来验证返回的解是否是最优的(例如,如果算法在面对异常值时产生了最准确的估计)或限制其次优性或准确性。为了实现这一目标，我们首先使用截断最小二乘( truncated least squares，TLS )cost重新计算配准问题，该cost使得估计对很大一部分伪对应不敏感。然后，我们提供了一个通用的图论框架来解耦尺度、旋转和平移估计，这允许对三种变换进行级联求解。尽管每个子问题(尺度、旋转和平移估计)在性质上仍然是各自非凸的且彼此耦合，但我们表明：

1. TLS尺度和(component-wise)平移估计，可以通过自适应投票方案在polynomial time内求解；
2. TLS旋转估计，可以 relax 为半正定规划( SDP )，即使在极端离群率的情况下，relaxation is tight；
3. 图论框架允许通过寻找最大团对离群值进行大幅度剪枝。我们将得到的算法命名为TEASER (截断最小二乘估计与半正定松弛)。

        由于求解大型SDP松弛通常是缓慢的，我们开发了第二个快速且可证明的算法，命名为TEASER++，它使用渐进非凸性来解决旋转子问题，并利用Douglas-Rachford Splitting来有效地证明全局最优性。对于这两种算法，我们都给出了估计误差的理论上界，这在robust registration问题中是第一种。此外，我们在公共开源数据集、目标检测数据集和3DMatch扫描匹配数据集上测试了它们的性能，结果表明：

1. 这两种算法在当前最先进的(例如, RANSAC ,分支定界,启发式等)中占主导地位，并且在尺度已知的情况下对超过99 %的异常值具有鲁棒性；
2. TEASER++ 可以在毫秒级运行，是目前最快的鲁棒配准算法；
3. TEASER++ 非常鲁棒，可以解决没有对应关系的问题(例如,假设所有的对应关系)。其中它在很大程度上优于ICP，它比Go-ICP更准确，同时速度快几个数量级。

Introduction

        点云配准point cloud registration(也称为扫描匹配scan matching或点云对齐point cloud alignment)是机器人学和计算机视觉中的一个基本问题，其核心是寻找使两片点云对齐的最佳变换(旋转、平移和潜在尺度)。它在运动估计和三维重建，物体识别和定位，全景图拼接，以及医学成像等方面都有应用。

        当点云之间的真实对应关系已知且点受零均值高斯噪声影响时，由于各向同性噪声情况下存在优美的闭式解[ 14 ]，[ 15 ]，配准问题可以很容易地解决。然而，在实际中，这些对应关系要么是未知的，要么包含许多异常值，导致这些求解器产生较差的估计。大的离群率是三维关键点检测和匹配的典型特征。（准确找到点云中的对应关系并不容易，这点跟视觉一样，前端特征匹配效果直接影响定位性能，后来视觉用上了深度学习，有可能点云配准也得走这条路）。

[14] B. K. P. Horn, “Closed-form solution of absolute orientation using unit quaternions,” J. Opt. Soc. Amer., vol. 4, no. 4, pp. 629–642, Apr. 1987.

[15] K. Arun, T. Huang, and S. Blostein, “Least-squares fitting of two 3D point sets,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 9, no. 5, pp. 698–700, Sep. 1987.

        通常使用的具有未知或不确定对应关系的配准方法要么依赖于未知变换(例如,迭代最近点, ICP )的初始猜测的可用性，要么隐含地假设存在一组小的异常值(例如, RANSAC )1。这些算法可能在没有预见[见图1 ( b )和( e )]的情况下失败，并且可能返回距离真实变换任意远的估计（也就是到达局部最优）。一般来说，文献分为启发式方法，即快速但脆弱的方法和保证鲁棒性的全局方法，但在最坏情况下运行需要耗费指数级的时间(例如,分支定界方法,如Go-ICP )。 

1.RANSAC的运行时间随着离群点比率的增加呈指数增长，并且当离群点比例较大时，RANSAC通常表现不佳。

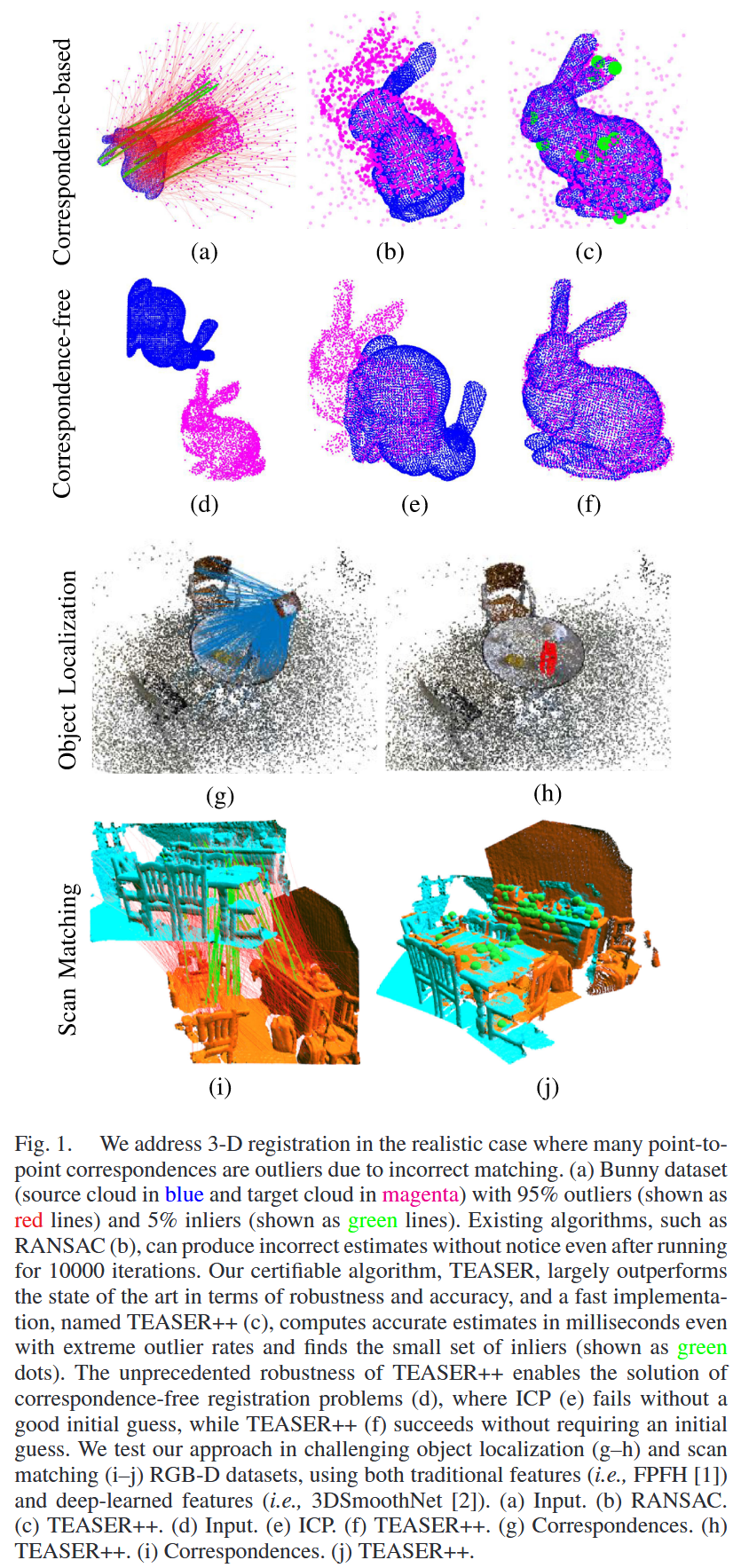
        本文的目标是设计一种方法，

1. 能够解决全局配准(不依赖于初始猜测initial guess)，
2. 能够容忍极端数量的异常值(例如,当99 %的对应关系为异常值时)，
3. 在多项式时间内运行，并且在实际(即,可以在机器人上实时操作)中运行速度快，
4. 提供良好的性能保证。

特别地，我们寻找一个后验保证，例如执行算法后可以检查的条件，以评估估计的质量。这就引出了可证明算法的概念，即一种试图求解的算法成为一个棘手的问题，并为其是否成功提供了可检验的条件。感兴趣的读者可以在[ 27 ]的附录A中找到更广泛的讨论。

[27] H. Yang, J. Shi, and L. Carlone, “TEASER: Fast and certifiable point cloud registration,” 2020, arXiv: 2001.07715.

         贡献：本文提出了第一个带离群点的三维配准可认证算法。我们使用截断最小二乘( TLS )代价(第四部分提出了)重新建模配准问题，该代价对一大部分虚假对应不敏感，但导致一个困难的、组合的和非凸的优化。

• 第一个贡献(见第五节)是一个解耦尺度、旋转和平移估计的通用框架。我们的方案的新颖之处有四点：
  • ( i )我们发展了不变量测量来估计尺度( 其他方法假设规模给定)，
  • ( ii )我们在未知但有界误差的假设下将解耦形式化，
  • ( iii )我们提供了一个通用的图论框架来推导这些不变量测量，
  • ( iv )我们证明了这个框架允许通过寻找由不变量测量(见第六节)定义的图的最大团来修剪大量的异常值。
• 解耦允许对尺度、旋转和平移进行级联求解。然而，每个子问题本质上仍然是组合的。我们的第二个贡献是证明了
  • 1 )在标量情况下，TLS估计可以使用自适应投票机制在多项式时间内精确求解，这使得对尺度和(分量)平移(见第七节)的有效估计成为可能；
  • 2 )我们可以建立一个紧半定规划( SDP )relaxation来估计旋转，并建立一个后验条件来检查松弛(见第八节)的质量。
  • 我们注意到，本文所解决的旋转子问题本身就是视觉(其中,称为旋转搜索)和航天(其中,称为Wahba问题)中的一个基础性问题。我们的SDP松弛是第一个可认证的鲁棒旋转搜索算法。
• 我们的第三个贡献(见第九节)是一组理论结果，证明了我们的算法返回的解的质量，称为截断最小二乘估计和半正定松弛( TEASER )。在无噪声的情况下，我们提供了易于检查的条件，在该条件下，TEASER可以在存在离群点的情况下恢复点云之间的真实变换。在有噪声的情况下，我们给出了地面真值转换与TEASER估计之间距离的界。据我们所知，这是第一个关于带有异常值的几何估计问题的非渐近误差界，而统计中关于稳健估计的文献(例如, )通常研究欧氏空间中的更简单的问题，并专注于渐近界。
• 我们的第四个贡献(见第十节)是实现了一个快速版本的TEASER，命名为TEASER++，它使用渐进非凸性( GNC ) 来估计旋转，而不需要求解一个大的SDP。我们证明了TEASER++也是可证明的，特别地，我们利用Douglas–Rachford Splitting ( DRS ) 设计了一个可扩展的最优性证明器，可以断言GNC返回的估计的全局最优性。我们发布了TEASER++的快速开源C + +实现。
• 我们的最后一个贡献(见第11节)在标准基准测试和真实数据集上进行了广泛的评估，用于目标检测和扫描匹配。特别地，我们证明了
  • 1 ) TEASER和TEASER++都超过当前SOTA的方法(例如, RANSAC ,分支定界,启发式等)，并且在尺度已知的情况下对超过99%的异常值具有鲁棒性；
  • 2 ) TEASER++可以在毫秒级运行，是目前最快的鲁棒配准算法；
  • 3 ) TEASER++非常鲁棒，它还可以解决没有对应关系的问题(例如,假设所有的对应关系)，其中它在很大程度上优于ICP，并且它比Go-ICP更准确，同时速度快几个数量级；
  • 4 ) TEASER++与深度学习的关键点检测和匹配相结合可以提高配准性能。（这一条很感兴趣，这给点云配准开辟了一条新路，也就是给激光SLAM开辟了一条新路，不过当然是四年前的路）

（太夸张了，从来没见过能写一整页贡献的，这就是TRO吗？这就是MIT吗？后面还有两段又描述了一下本文的创新点和行文结构，太夸张了，写了11章）

Related Works

        对于三维点云的配准，目前比较流行的有两种方法：Correspondence-based的方法和Simultaneous Pose and Correspondence(SPC) (即,correspondence-free)方法。

A. Correspondence-Based Methods

        基于对应关系的方法首先使用特征描述子[ FPFH等 ]检测和匹配点云之间的三维关键点，然后使用估计器从这些假定的对应关系中推断转换。与SIFT和ORB等2D关键点匹配相比，3D关键点匹配的准确性较低，因此导致了更高的离群率，例如95%的伪匹配被认为是常见的[ 19 ]。因此，一个能够处理极端离群率的稳健后端是非常可取的。

[19] Á. Parra Bustos and T. J. Chin, “Guaranteed outlier removal for point cloud registration with correspondences,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 40, no. 12, pp. 2868–2882, Dec. 2018.

       Registration Without Outliers：有文献证明当对应点已知且点受各向同性的零均值高斯噪声影响时，尺度、旋转和平移的最优解(在最大似然意义下)可以用闭合形式计算。基于分支定界( Branch-and-bound，BnB )的方法，该方法是全局最优的，并且允许点对点，点对线和点对面的对应。

        如果两组点仅相差一个未知的旋转(也就是说,我们不试图估计尺度和平移)，则得到一个简化版本的配准问题，即计算机视觉中的旋转搜索，或航空航天中的Wahba问题。在航天航空中，矢量观测通常是卫星上传感器观测到的指向可见星的方向。利用四元数和旋转矩阵的表示，Wahba问题的闭式解是已知的。Wahba问题也与著名的正交Procrustes问题有关，即寻找正交矩阵(而不是旋转)，该问题也存在闭式解。计算机视觉领域已经研究了点云配准，图像拼接，运动估计和三维重建。特别地，Horn [ 14 ]和Arun等[ 15 ]（参考文献见上）的闭式解可用于各向同性高斯噪声下的(无异常值)旋转搜索。针对各向异性高斯噪声的情况……（存在一些远古数学大神的论文中。。。这里并非本文的阅读目的）

        Robust Registration：可能最广泛使用的鲁棒配准方法是基于RANSAC。尽管RANSAC在低噪声和低离群点的情况下是有效的，但在离群率较大的情况下，RANSAC表现出收敛速度慢和精度低，其中采样一个"好"的consensus set变得更加困难。另一些方法采用M估计，也就是用对异常值不太敏感的鲁棒代价函数代替最小二乘目标函数。[ 56 ]提出了快速全局配准( FGR )，使用GemanMcClure代价函数，并利用GNC来解决产生的非凸优化。尽管FGR是有效的，但它并没有提供最优性保证。事实上，正如我们在第11节中所示，当异常比率较高( > 80 % )时，FGR往往会失败。Parra和Chin [ 19 ]提出了保证离群点移除( Guaranteed Outlier REmoval，GORE )技术，在将离群点对应传递到优化后端之前，使用几何操作来显著减少离群点对应的数量。GORE已被证明对95 %的伪对应具有鲁棒性[ 19 ]。在一项独立的工作中，Parra等人[ 58 ]使用实用的最大团( PMC )算法在三维配准中发现了成对一致的对应关系。虽然在精神上与我们最初的提议相似[ 39 ]，但GORE和PMC都没有估计配准的尺度，而且由于它们依赖于BnB (见文献[ 19 ,算法2 ])，所以速度通常较慢。Yang和卡洛内[ 39 ]提出了第一个可认证的鲁棒配准算法，但该算法需要求解一个大规模的SDP，因此仅限于小问题。

[56] Q. Zhou, J. Park, and V. Koltun, “Fast global registration,” in Proc. Eur. Conf. Comput. Vis., 2016, pp. 766–782.

[19] Á. Parra Bustos and T. J. Chin, “Guaranteed outlier removal for point cloud registration with correspondences,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 40, no. 12, pp. 2868–2882, Dec. 2018.

58] A. Parra Bustos, T.-J. Chin, F. Neumann, T. Friedrich, and M. Katzmann, “A practical maximum clique algorithm for matching with pairwise constraints,” 2019, arXiv:1902.01534.

[39] H. Yang and L. Carlone, “A polynomial-time solution for robust registration with extreme outlier rates,” in Proc. Robot.: Sci. Syst., 2019. [Online]. Available: http://rss2019.informatik.unifreiburg.de/papers/0013_FI.pdf(pdf), http://rss2019.informatik.unifreiburg.de/videos/0013_VI_fi.mp4(video), http://news.mit.edu/ 2019/spotting-objects-cars-robots-0620(media), https://www. sciencedaily.com/releases/2019/06/190620121444.htm(media), http://www.ansa.it/canale_scienza_tecnica/notizie/tecnologie/20 19/ 06/21/i-robot-imparano-a-vedere-nella-nebbia-_9e59485c-ff17-4d628224-1d42f 44111b9.html(media)

        与配准问题类似，带离群点的旋转搜索也在计算机视觉领域得到了研究。用于鲁棒旋转搜索的局部技术也是基于RANSAC或M估计，但很脆弱，并没有提供性能保证。全局方法(保证计算出全局最优解)基于Consensus Maximization共识最大化和BnB。BnB可以保证返回全局最优解，但在最坏情况下，它以指数时间运行。另一类全局一致性最大化方法枚举所有可能的测量子集，其大小不超过问题维度(三个用于旋转搜索)，解析计算候选解，然后使用计算几何验证全局最优性。类似地，TLS估计也可以通过枚举规模不大于模型维数的子集来全局求解。然而，这些方法需要穷举，当问题维数(例如, 6用于3D配准)较大时变得棘手。在[ 40 ]中，我们提出了第一个基于四元数的鲁棒旋转搜索可认证算法。

40] H. Yang and L. Carlone, “A quaternion-based certifiably optimal solution to the Wahba problem with outliers,” in Proc. Int. Conf. Comput. Vis. (ICCV), 2019.

（搞机器人、计算机这些做应用的和在搞数学的人面前真是太渺小了……这都是什么玩意……学个机器人算法或者计算机算法就焦头烂额了） 

B. Simultaneous Pose and Correspondence Methods

        SPC方法在寻找对应关系和计算给定对应关系的最佳变换之间交替进行。

       Local Methods：迭代最近点( Iterative Closest Point，ICP )算法被认为是点云配准的里程碑。然而，ICP容易收敛到局部极小值，只有在良好的初始猜测下才能表现出良好的性能。ICP的多个变体都提出使用鲁棒代价函数来提高收敛性。概率解释也被提出来改进ICP，即最小化两个混合模型之间的Kullback–Leibler散度。Clark等人[ 79 ]使用黎曼优化Riemannian optimization将点云对齐为连续函数。[ 80 ]使用半定松弛为随机方法生成假设。所有这些方法都不能提供全局最优性保证。

[79] W. Clark, M. Ghaffari, and A. Bloch, “Nonparametric continuous sensor registration,” 2020, arXiv:2001.04286.

[80] H. M. Le, T.-T. Do, T. Hoang, and N.-M. Cheung, “SDRSAC: Semidefinite-based randomized approach for robust point cloud registration without correspondences,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2019, pp. 124–133.

        Global Methods: 全局SPC方法在没有初始猜测的情况下计算全局最优解，通常基于BnB。一系列的几何技术被提出来改善边界紧密度[ 20 ]（太老的方法就不引用了）和提高搜索速度[ 20 ]。然而，BnB的运行时间随点云规模呈指数增长，并且由于高离群率导致的局部极小值数量激增而变得更糟[ 19 ]。全局SPC注册也可以描述为一个混合整数规划[ 84 ]，尽管运行时间仍然是指数级的。Maron等人[ 85 ]设计了一个紧半定松弛，然而，该松弛仅适用于完全重叠的SPC配准。 

[20] J. Yang, H. Li, D. Campbell, and Y. Jia, “Go-ICP: A globally optimal solution to 3D ICP point-set registration,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 38, no. 11, pp. 2241–2254, Nov. 2016. 

[84] G. Izatt, H. Dai, and R. Tedrake, “Globally optimal object pose estimation in point clouds with mixed-integer programming,” Robot. Res., 2020, pp. 695–710.

[85] H. Maron, N. Dym, I. Kezurer, S. Kovalsky, and Y. Lipman, “Point registration via efficient convex relaxation,” ACM Trans. Graph., vol. 35, no. 4, pp. 1–12, 2016.

       Deep Learning Methods（会是真神降临吗？）: 深度学习在三维点云(例如,PointNet和DGCNN )上的成功为从数据中学习点云配准打开了新的机会。深度学习方法首先学习在高维特征空间中嵌入点云，然后学习匹配关键点生成对应关系，然后在刚性变换空间上进行优化以获得最佳对齐效果。PointNetLK[88]使用点网络学习特征表示，然后迭代地对齐特征表示，而不是三维坐标。DCP [ 89 ]使用DGCNN特征进行对应匹配，使用Horn方法进行端到端的配准( Horn方法是可微的)。 PRNet将DCP扩展到对齐部分重叠的点云。Scan2CAD及其改进[ 92 ]使用类似的pipeline将CAD模型对齐到RGB-D scans。3DSmoothNet使用孪生深度学习架构在两个点云之间建立关键点对应关系。FCGF利用稀疏的高维卷积从点云中提取稠密的特征描述子。Deep global registration[ 93 ]采用FCGF特征描述子进行点云配准。在第11节中，我们展示了1 )我们的方法为深度学习的关键点匹配算法(我们用【2】 )提供了一个robust的后端，2 )当前的深度学习方法在实际问题中仍然难以产生可接受的内点率。

[88] Y. Aoki, H. Goforth, R. A. Srivatsan, and S. Lucey, “Pointnetlk: Robust & efficient point cloud registration using PointNet,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2019, pp. 7163–7172.

[89] Y. Wang and J. M. Solomon, “Deep closest point: Learning representations for point cloud registration,” in Proc. Int. Conf. Comput. Vis., 2019, pp. 3523–3532.

[92] A. Avetisyan, A. Dai, and M. Nießner, “End-to-End CAD model retrieval and 9DoF alignment in 3D scans,” in Proc. Int. Conf. Comput. Vis., 2019, pp. 2551–2560.

[93] C. Choy, W. Dong, and V. Koltun, “Deep global registration,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2020, pp. 2511–2520.

[2] Z. Gojcic, C. Zhou, J. D. Wegner, and A. Wieser, “The perfect match: 3d point cloud matching with smoothed densities,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2019, pp. 5545–5554.

        注1 (Correspondence-based和SPC方法的协调)：Correspondence-based的方法和SPC方法是紧密耦合的。首先，类似ICP的方法在寻找对应关系和解决对应基问题之间交替进行。更重要的是，人们总是可以重新表述一个SPC该问题是一个基于对应关系的问题，通过假设所有点到所有点的对应关系，即把第一个点云中的每个点关联到第二个点云中的所有点。但是它导致了极端数量的异常值。在本文中，我们证明了我们的方法确实可以解决SPC问题，这得益于其对异常值(见第11节)前所未有的鲁棒性。

III. NOTATIONS AND PRELIMINARIES

Scalars, Vectors, Matrices

 Sets

Quaternions

        四元数是表示3D旋转的一种数学工具，特别在 SO(3)（3维旋转群）中有广泛应用。论文中定义了单位四元数，并详细描述了其表示和运算。

 IV. ROBUST REGISTRATION WITH TRUNCATED LEAST SQUARES COST

1. 问题背景

Registration Without Outliers:

 Truncated Least Squares Registration:

Remark 2 (TLS versus Consensus Maximization)

Remark 3 (Hardness of TLS Estimation):

 V. DECOUPLING SCALE, ROTATION, AND TRANSLATION ESTIMATION

        论文提出了一种解耦方法，用于解决截断最小二乘（TLS）配准问题，即估计尺度 s 、旋转 R∈SO(3) 和平移  。关键洞察是通过重新构造测量值），得到对某些变换（尺度、旋转或平移）不变的量，从而将问题分解为三个子问题，分别估计 s 、R 和 t 。这种不变测量（invariant measurements）的方法降低了问题的复杂性，尤其是在存在大量异常值的情况下。

A. Translation Invariant Measurements (TIMs)

（这怎么能直接减呢？假设两个点云位于同一个坐标系吗，如果是两激光帧相减还好。如果是全局坐标系下的两个点云，scan-to-map这能减吗？）

Theorem 4 (Translation Invariant Measurements)

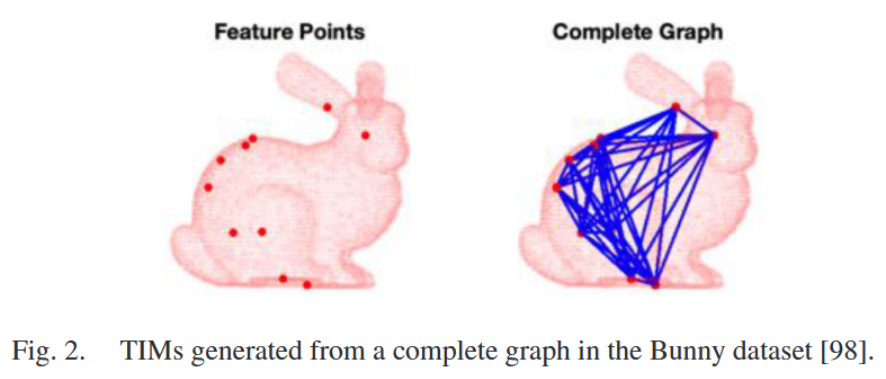
 B. Translation and Rotation Invariant Measurements (TRIMs)

Remark 5 (Novelty of Invariant Measurements)

• TIM的创新：虽然TIM的概念在众多文献中出现过，但定理4的图论解释是新的，允许基于图结构剪枝异常值。
• TRIM的创新：TRIM是本文提出的全新概念，用于尺度估计。
• 应用：不变测量不仅用于过滤异常值或加速分支定界（Branch-and-Bound, BnB），还用于解耦尺度、旋转和平移估计。

VI. TRUNCATED LEAST SQUARES ESTIMATION AND SEMIDEFINITE RELAXATION (TEASER): OVERVIEW

（理论工具已经备好，终于步入正题！）

 1. TEASER算法概述

TEASER（Truncated least squares Estimation And SEmidefinite Relaxation）是一种级联方法，按以下步骤解耦和解决TLS配准问题：

1. 使用TRIM估计尺度  。
2. 使用估计的 和TIM估计旋转  。
3. 使用 、 和原始点对 估计平移  。

A. Robust Scale Estimation

 B. Robust Rotation Estimation

C. Robust Component-Wise Translation Estimation

（这么看，虽然理论工具很吓人，但是算法流程其实很简单也很明确，先求尺度，再求旋转，最后求平移。对于激光来说，尺度是一致的，不需要求。问题就变成了先旋转后平移问题） 

D. Boosting Performance: Max Clique Inlier Selection (MCIS)

E. Pseudocode of TEASER

算法1总结了TEASER的流程：

1. 使用TRIM估计尺度 （调用 estimate_s）。
2. 使用 和TIM估计旋转 （调用 estimate_R）。
3. 使用 、 和原始点对估计平移 （调用 estimate_t）。
4. 可选：在尺度估计后，通过最大团剪枝异常值。

（这个过程还是很清晰和简单的，虽然证明和推导过程非常繁琐） 

VII. ROBUST SCALE AND TRANSLATION ESTIMATION: ADAPTIVE VOTING

A. Adaptive Voting for Scalar TLS Estimation

        自适应投票（Adaptive Voting）算法，用于精确求解标量TLS问题，即鲁棒尺度估计（公式11）和分量式平移估计（公式13）。这两个问题本质上都是在存在异常值的测量数据中估计一个标量（尺度 s 或平移分量 tj），通过自适应投票算法可以在多项式时间内获得全局最优解。

 Theorem 7 标量TLS估计的最优解

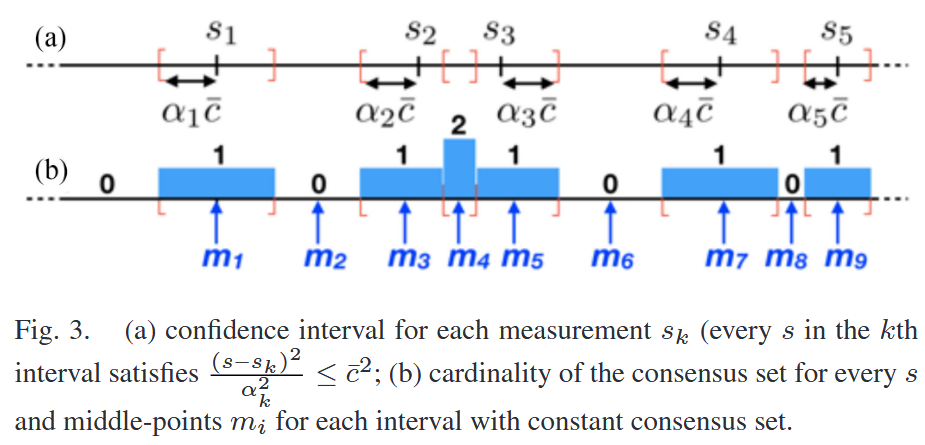
Remark 8 (Adaptive Voting)

• 自适应投票算法是对Scaramuzza 的直方图投票方法的推广：
  • 直方图投票使用固定bin大小，可能无法精确求解TLS。
  • 自适应投票动态调整bin大小（基于噪声界  ​），保证全局最优。
• 自适应投票也可用于一致性最大化（Consensus Maximization），只需返回最大的一致集 Ii。

应用：

• 尺度估计：函数 estimate_s 调用算法2计算 。
• 平移估计：函数 estimate_t 对 t1,t2,t3 ​分别调用算法2三次，得到   。

 VIII. ROBUST ROTATION ESTIMATION: SEMIDEFINITE RELAXATION AND FAST CERTIFICATES

1. 概述

 A. Robust Rotation Estimation as a QCQP

B. Semidefinite Relaxation

C. Fast Global Optimality Certification

        解决大型SDP（公式23）计算成本高（例如，使用MOSEK求解 K=100 时需约1200秒）。而快速启发式算法（如GNC）可在毫秒内提供高质量解，但无法保证全局最优。论文提出快速全局最优认证（fast optimality certification），验证给定旋转估计是否为全局最优。

 （已经没有耐心了，快直接告诉我结论！这个算法又快又准又好用！）

IX. PERFORMANCE GUARANTEES

第IX节为TEASER算法提供了理论性能保证，基于之前的定理（7、13、14）分析TEASER估计结果与真实变换（ground truth）的偏差。分析分为两种情况：

• 无噪内点（noiseless inliers）：仅考虑异常值（outliers），分为随机异常值和对抗性异常值。
• 有噪内点（noisy inliers）：同时考虑噪声和异常值，提供更弱但更现实的界限。

A. Exact Recovery With Outliers and Noiseless Inliers

 B. Approximate Recovery With Outliers and Noisy Inliers

X. TEASER++: A FAST C++ IMPLEMENTATION

TEASER++是TEASER算法的快速C++实现，旨在展示其在机器人、计算机视觉和图形学中的实时应用能力。TEASER++开源，通过优化算法和实现细节，实现毫秒级运行时间，同时保留理论保证。

2. 实现细节

• 算法框架：遵循第VI节的解耦方法（尺度 → 旋转 → 平移），但对旋转估计进行了优化：
  • 避免直接求解大型SDP（公式23，计算成本高，例如 K=100 时需约1200秒）。
  • 使用GNC（Graduated Non-Convexity）快速求解TLS旋转估计问题（公式12），然后通过算法3（快速认证）验证全局最优性。
• 高效性原因：
  • 尺度估计（第VI-A节）和最大团内点选择（第VI-D节）已移除大部分异常值，使GNC只需处理较少的异常值（GNC在异常值率 <80% 时表现优异 ）。
  • 结合快速启发式（GNC）和可扩展的认证算法（DRS），TEASER++实现快速且可认证的配准。
• 优化技术：
  • 线性代数：使用Eigen3库进行高效矩阵运算。
  • 并行计算：通过OpenMP并行化算法2（自适应投票）、TIM/TRIM计算和最大团寻找 。
  • 最大团算法：采用快速精确的并行最大团算法 ，优化异常值剪枝。
• 接口与集成：
  • 提供Python和MATLAB绑定，便于快速原型设计和可视化。
  • 提供ROS封装，支持实时机器人应用。

3. 核心特点

• 快速性：TEASER++在实际问题中运行时间为毫秒级，远快于直接求解SDP。
• 可认证性：通过算法3验证GNC解的全局最优性，保留第IX节的性能保证。
• 开源性：开放源代码，增强可复现性和应用范围。

实验

硬件平台

i7-8850H CPU，32GB RAM笔记本电脑（部分实验在Xeon Platinum 8259CL服务器上，12线程）。

数据集

使用Stanford 3-D扫描存储库中的Bunny、Armadillo、Dragon、Buddha点云 [98]

[98] B. Curless and M. Levoy, “A volumetric method for building complex models from range images,” in Proc. SIGGRAPH, 1996, pp. 303–312.

Benchmark

• TEASER、TEASER++。
• FGR（Fast Global Registration） [56]。
• GORE（Guaranteed Outlier Removal） [19]。
• RANSAC（两种变体：RANSAC1K（1000次迭代），RANSAC1min（60秒超时））。

B. Benchmarking on Standard Datasets

1. 实验设置

• 数据集：Stanford 3-D扫描存储库的Bunny、Armadillo、Dragon、Buddha，下采样至 N=100个点。
• 比较方法：
  • TEASER、TEASER++。
  • FGR（Fast Global Registration） [56]。
  • GORE（Guaranteed Outlier Removal） [19]。
  • RANSAC（两种变体：RANSAC1K（1000次迭代），RANSAC1min（60秒超时））。
• 协议：与XI-A相同，测试Bunny数据集。
• 评估指标：旋转误差、平移误差、运行时间。

2. 已知尺度（s=1 ）

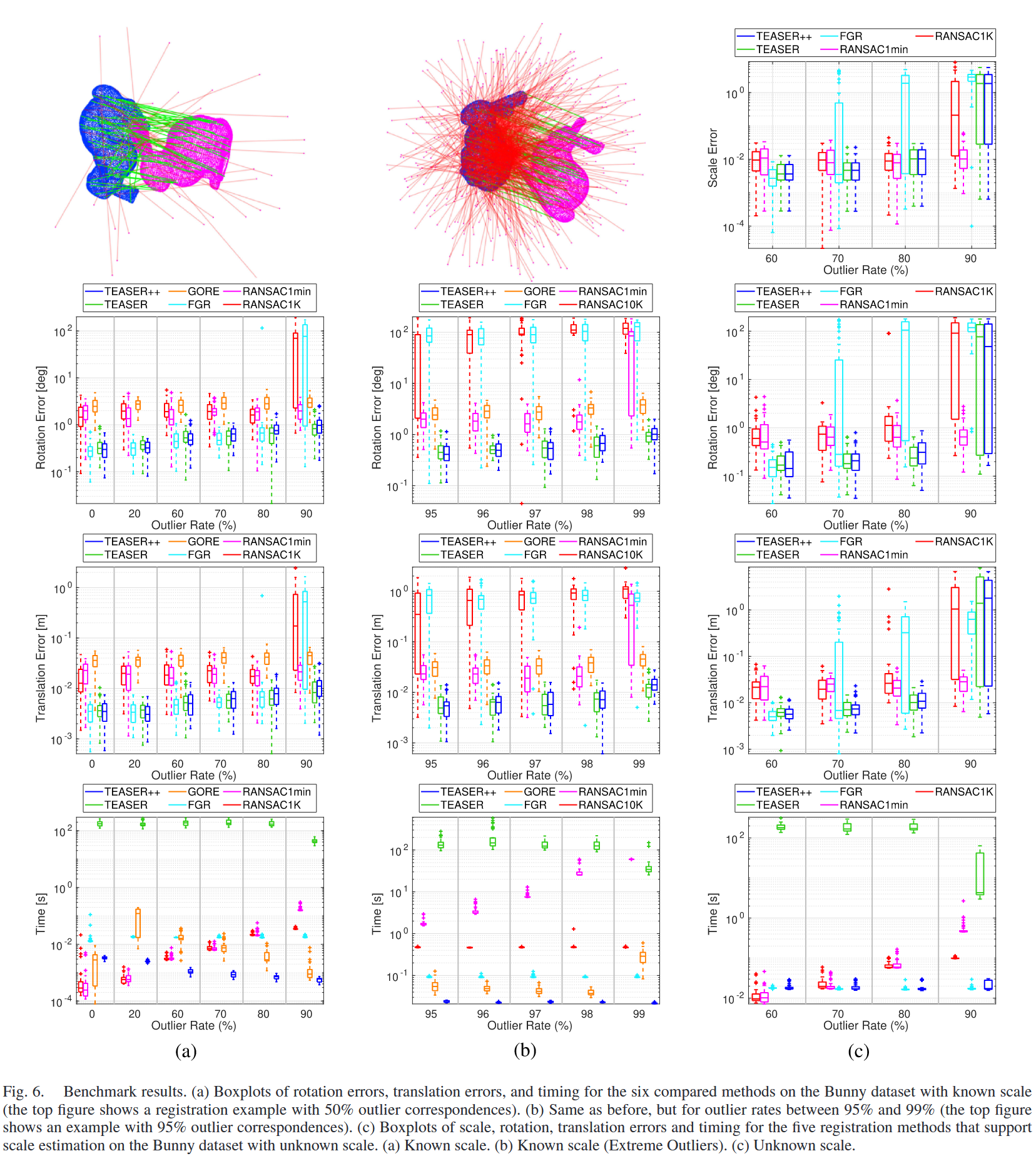
• 结果（图6(a)）：
  • TEASER、TEASER++、GORE、RANSAC1min在高达90%异常值率下鲁棒，TEASER和TEASER++精度高于GORE。
  • FGR在70%异常值率崩溃，RANSAC1K在90%崩溃。
  • TEASER++运行时间 <10ms，远快于TEASER（不适合实时应用）。
• 分析：
  • TEASER++的快速性和鲁棒性得益于GNC+算法3的组合，MCIS进一步降低了异常值率。
  • RANSAC1min需 >10^5 次迭代才能在90%异常值率下收敛，效率低。
  • 定理16（第IX节）解释了TEASER在高内点比例下的精确恢复能力。

3. 极端异常值率（95%–99%）

• 设置：N=1000 ，RANSAC1K替换为RANSAC10K。
• 结果（图6(b)）：
  • TEASER、TEASER++、GORE鲁棒至99%异常值率，TEASER和TEASER++误差更低。
  • RANSAC1min在98%异常值率下有效（10^6 次迭代），RANSAC10K和FGR表现较差。
  • TEASER++运行时间比GORE快一个数量级。
• 分析：
  • MCIS将异常值率降至 <10%，使TEASER++能在极端条件下保持高精度。
  • 定理15（第IX节）支持随机异常值下只需少量内点的精确恢复。

4. 未知尺度

• 结果（图6(c)）：
  • 所有方法在 <60% 异常值率下表现良好。
  • FGR在70%崩溃，RANSAC1K、TEASER、TEASER++在90%失败。
  • RANSAC1min在90%表现最佳，但需 >10^5 次迭代。
  • TEASER++运行时间 <30ms。
• 分析：
  • 未知尺度增加了问题难度，需更多内点（定理17）。
  • TEASER++的快速性和鲁棒性使其适合实时应用。

C. Simultaneous Pose and Correspondences (SPC)

1. 实验设置

• 任务：无对应关系时求解配准（SPC问题）。
• 方法：下采样Bunny至 N=100 N = 100 N=100，应用随机旋转和平移，移除部分点模拟部分重叠（例如，80%重叠移除20%点）。比较：
  • TEASER++：生成所有可能的对应关系（∣A∣⋅∣B∣≈104 |A| \cdot |B| \approx 10^4 ∣A∣⋅∣B∣≈104）。
  • ICP：初始为单位变换。
  • Go-ICP [20]：尝试30%、60%、90%修剪比例。
• 评估：旋转误差、平移误差、运行时间。

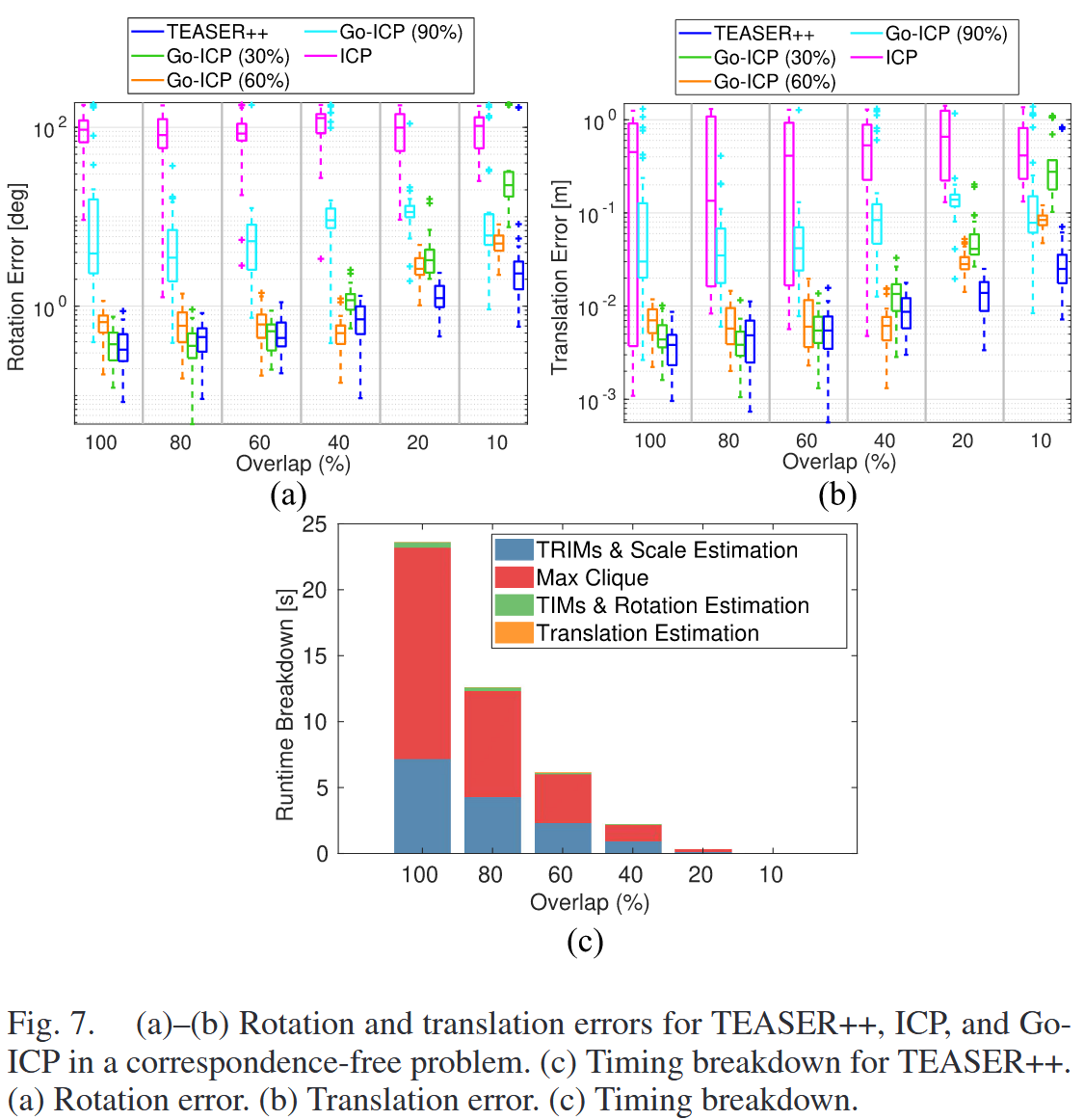
2. 结果（图7(a)、7(b)）

• ICP几乎全部失败，因初始猜测不在最优解的收敛域。
• Go-ICP（全局方法）表现优于ICP，但对修剪比例敏感，60%修剪最佳但仍不如TEASER++。
• TEASER++在重叠率 >10% 时成功，运行时间随对应数量增加而增加（图7(c)）。
• TEASER++比Go-ICP快数个数量级（Go-ICP平均16秒）。

3. 分析

• TEASER++通过MCIS和TLS处理大量异常对应关系，验证了定理15和16的鲁棒性。
• Go-ICP需用户指定修剪比例，限制了通用性。
• TEASER++在低重叠率（<40%）下的快速性得益于高效的最大团和尺度估计（图7(c)）。

D. Application 1: Object Pose Estimation and Localization

. 实验设置

• 数据集：[37] 的大规模点云数据集，提取谷物盒/帽作为物体，应用随机变换生成场景-物体对。
• 方法：使用FPFH特征描述子建立初始对应，TEASER计算相对位姿。下采样物体和场景至2000点。
• 评估：旋转误差、平移误差、FPFH对应数量、内点比例。

[37] K. Lai, L. Bo, X. Ren, and D. Fox, “A large-scale hierarchical multi-view RGB-D object dataset,” in Proc. IEEE Int. Conf. Robot. Autom., 2011, pp. 1817–1824. 

2. 结果（图8、表I）

• 内点比例 <10%（通常 <5%）。
• TEASER成功定位谷物盒，误差低（表I列出八个场景的均值和标准差）。
• 附录T [27] 提供八个场景的定性结果。

3. 分析

• 低内点比例验证了TEASER在极端异常值率下的鲁棒性（定理15）。
• FPFH对应质量较差，但TEASER通过MCIS和TLS有效识别内点。

 E. Application 2: Scan Matching

• 数据集：3DMatch数据集 [38]，包含62个室内RGB-D场景（54训练，8测试），每场景5000个关键点。
• 方法：
  • 使用3DSmoothNet [2] 计算关键点局部描述子，通过最近邻搜索生成对应。
  • 比较TEASER++、RANSAC1K、RANSAC10K、TEASER++ (CERT)（使用算法3，次优界 $$ \eta = 3% \））。
• 评估：成功匹配比例（旋转误差 <10°，平移误差 <30cm），运行时间。
• 环境：Xeon Platinum 8259CL服务器，12线程，( \beta_i = 5\text{cm} $$。

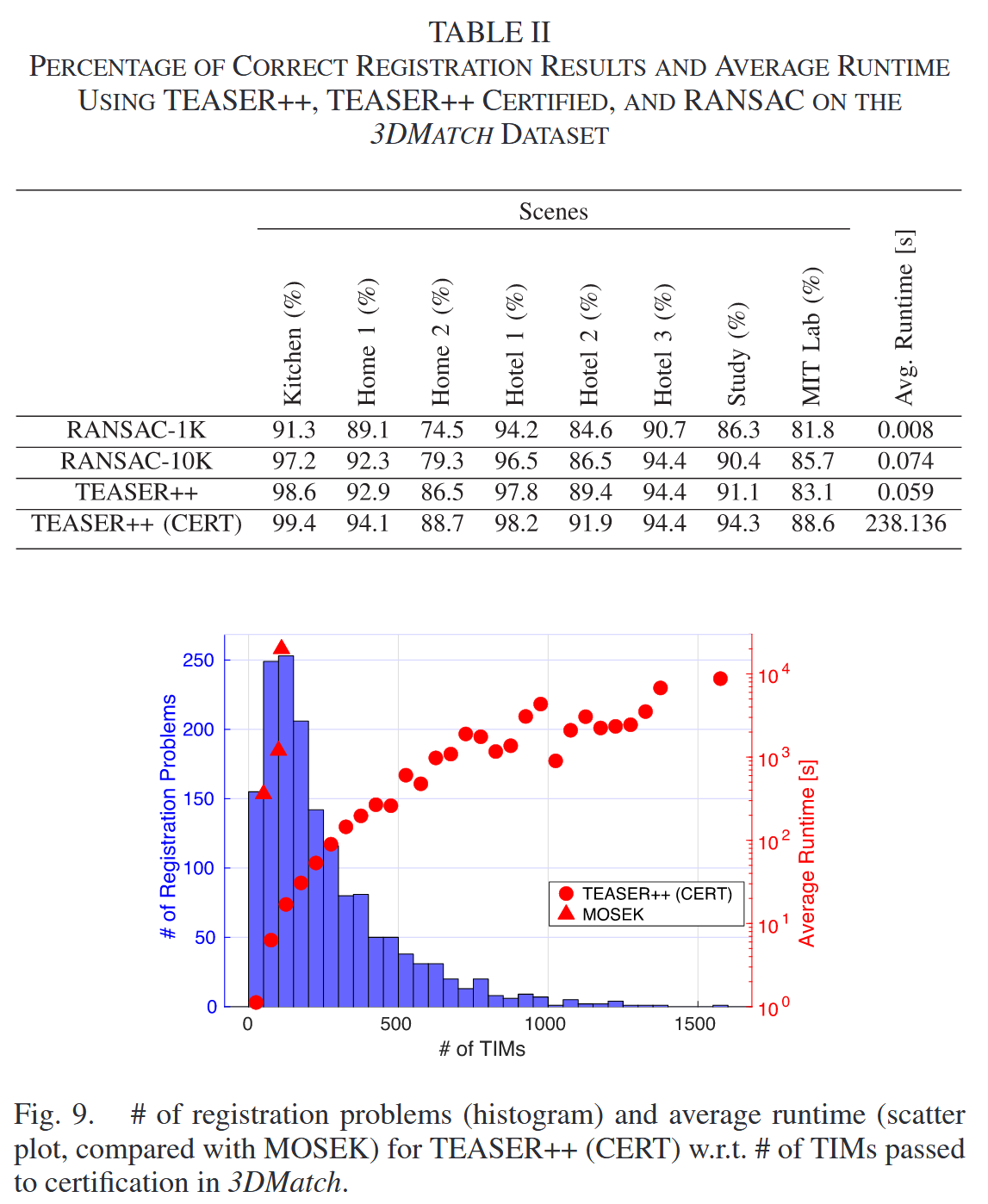
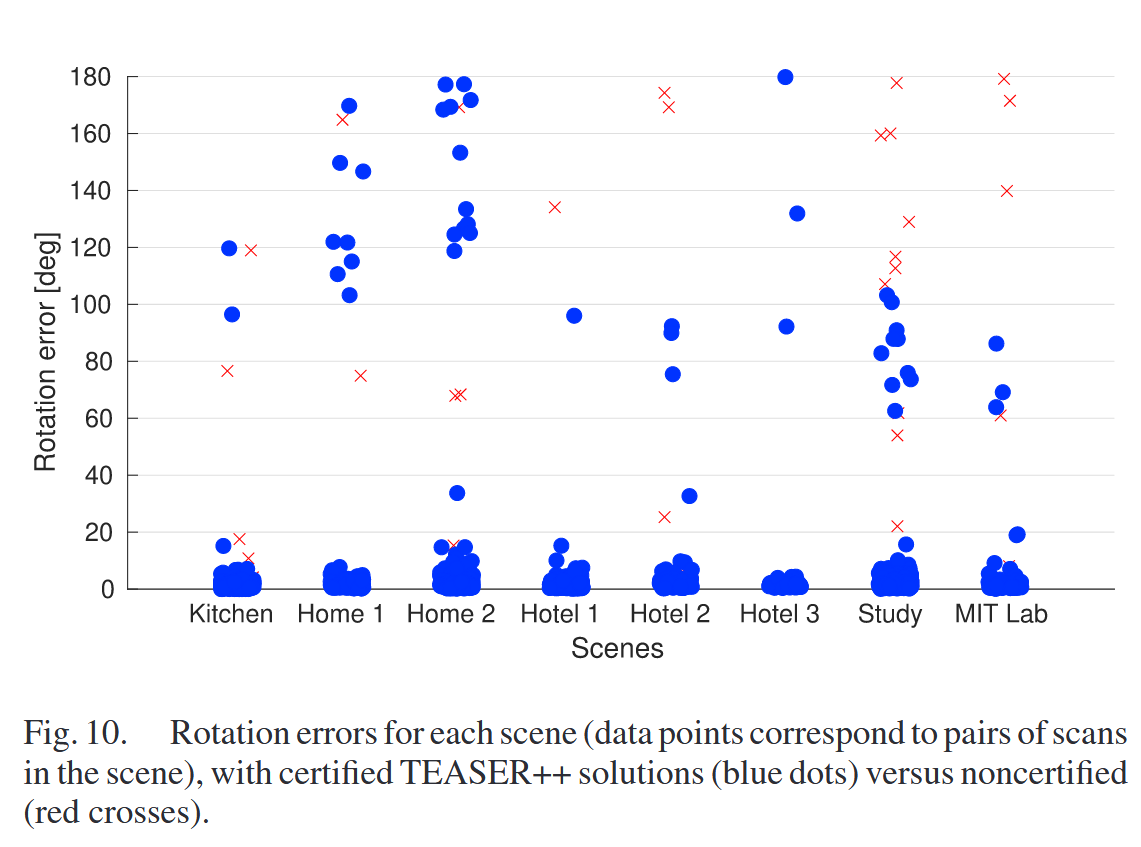
2. 结果（表II、图9、10、11）

• 成功率：TEASER++优于RANSAC1K（差最高12%）和RANSAC10K（多数场景更精确）。TEASER++ (CERT)严格优于其他方法，因其拒绝不可靠结果。
• 运行时间：TEASER++平均 <100秒，TEASER++ (CERT) <200秒，远快于MOSEK（>150 TIMs时内存不足）。
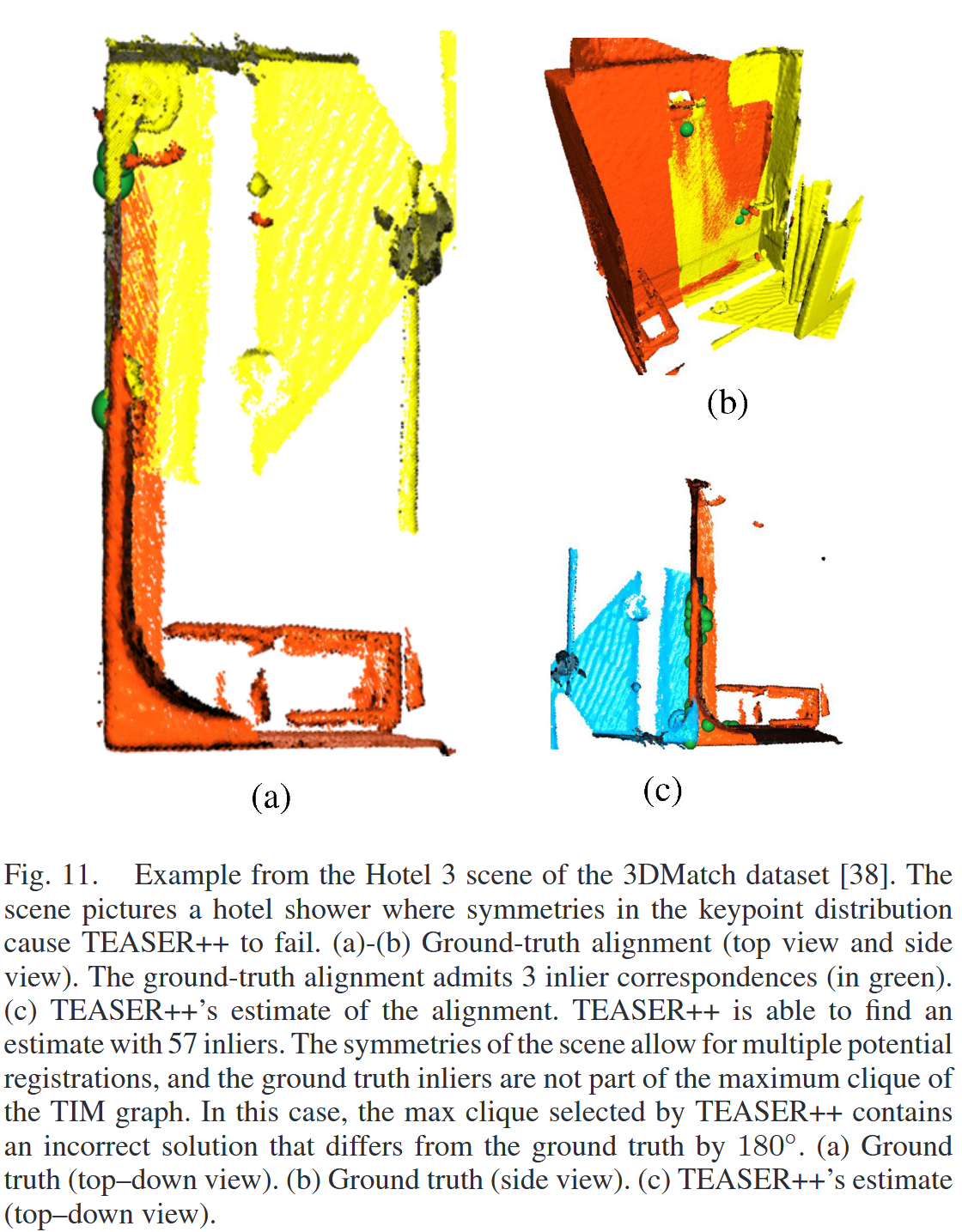
• 失败原因（图10、11）：
  • 关键点描述子质量差，导致无内点或内点不足（<3个，定理15–17）。
  • 场景对称性导致非唯一配准（误差约90°或180°）。
• 认证效率（图9）：TEASER++ (CERT)比MOSEK快数个数量级，50 TIMs认证时间1.12秒。

3. 分析

• TEASER++的鲁棒性得益于MCIS和GNC+算法3的组合，适合SLAM中的循环闭合检测。
• TEASER++ (CERT)通过拒绝错误配准提升可靠性，验证了定理14的认证能力。
• 失败案例凸显了深度学习关键点检测的局限性，需改进描述子质量。

总结： 

• 模块性能（XI-A）：
  • 尺度、平移估计在80%异常值率下鲁棒，符合定理15–17。
  • MCIS将异常值率降至 <10%，支持后续估计的高效性。
  • 四元数SDP优于旋转矩阵SDP，GNC+算法3在TEASER++中平衡了速度和精度。
• 基准测试（XI-B）：
  • TEASER++在已知和未知尺度下均表现优异，运行时间 <30ms，适合实时应用。
  • 极端异常值率（99%）下仍保持鲁棒，验证了定理15的理论保证。
• SPC问题（XI-C）：
  • TEASER++无需初始猜测，优于ICP和Go-ICP，验证了其处理大量异常对应的能力。
• 应用（XI-D、XI-E）：
  • 物体定位和扫描匹配展示了TEASER在低内点比例下的实用性。
  • TEASER++ (CERT)通过认证提升SLAM可靠性。

（原来作者本科是清华的，中国人！我说怎么这么牛逼！）

初体验

TODO