深度学习（鱼书）day03--神经网络（后两节）

深度学习day02–神经网络（后两节）

一、3层神经网络的实现

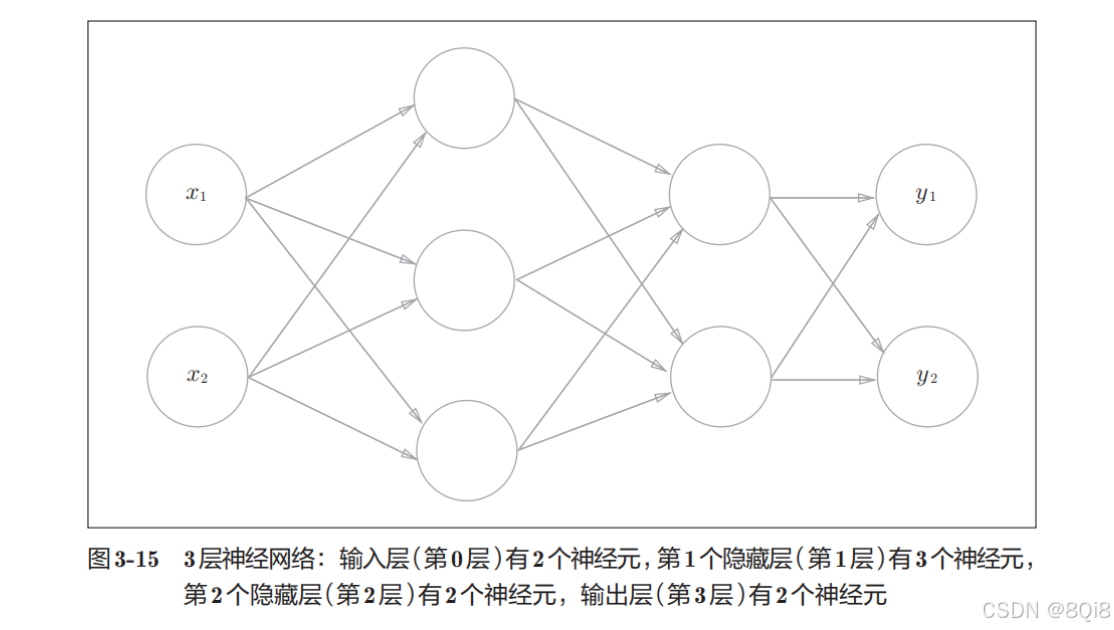
以下图的3层神经网络为对象，实现从输入到输出的（前向）处理。

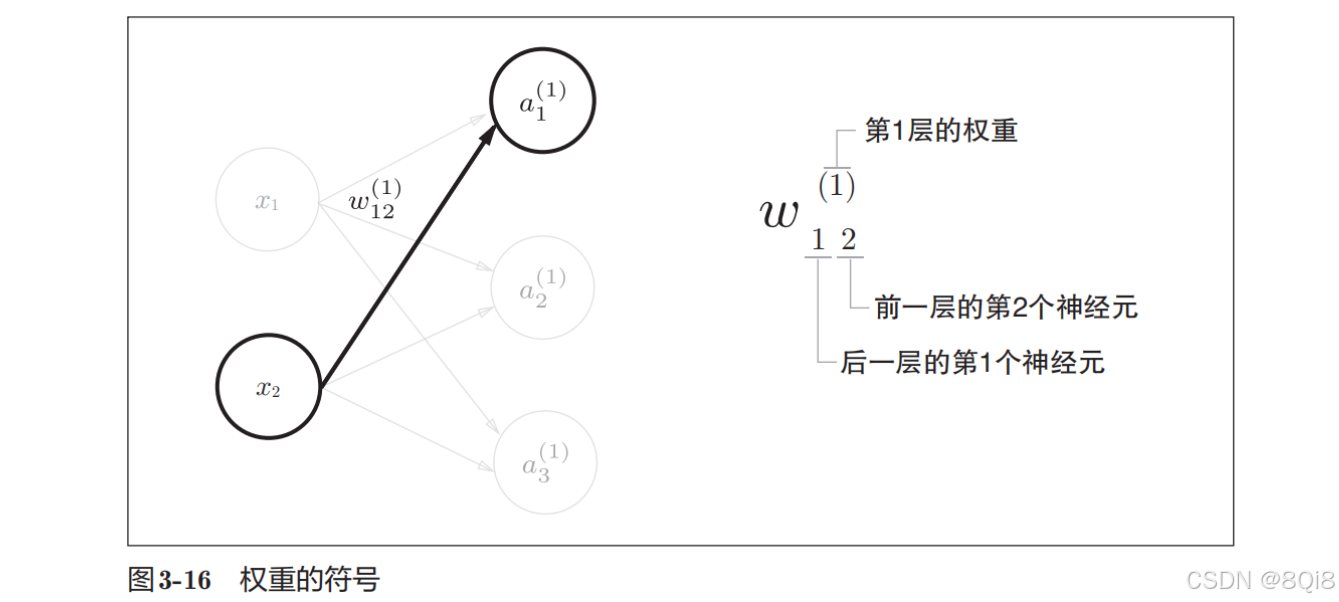
1. 符号确认

2. 各层间信号传递的实现

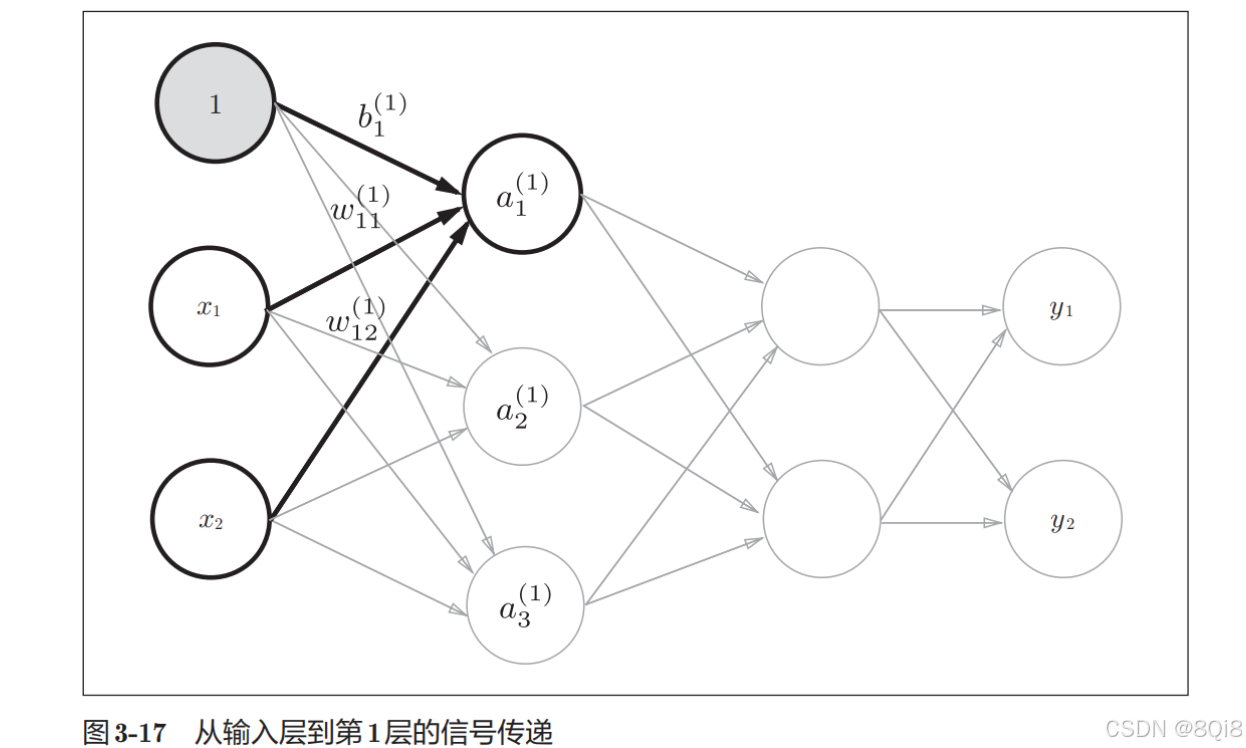
任何前一层的偏置神经元“1”都只有一个。偏置权重的数量取决于后一层的神经元的数量（不包括后一层的偏置神经元“1”）。

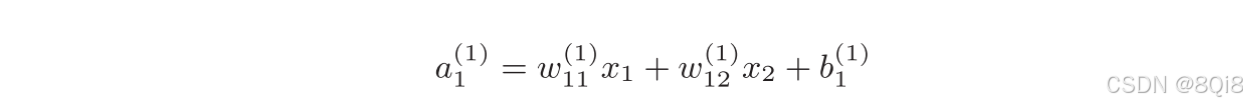
如果使用矩阵的乘法运算，则可以将第1层的加权和表示成下面式子：

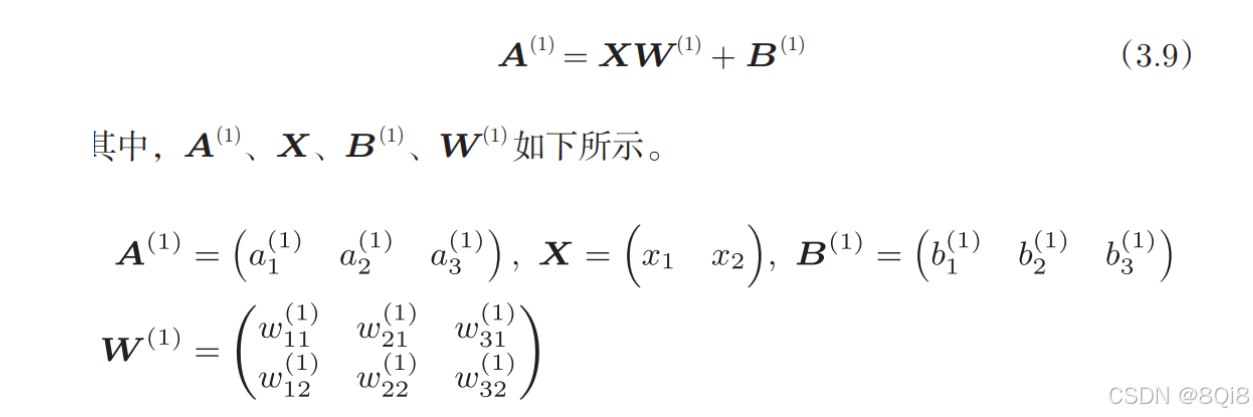
计算过程：

这里将输入信号、权重、偏置设置成任意值。

X = np.array([1,0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
print(W1.shape) # (2, 3)
print(X.shape) # (2,)
print(B1.shape) # (3,)
A1 = np.dot(X, W1) + B1

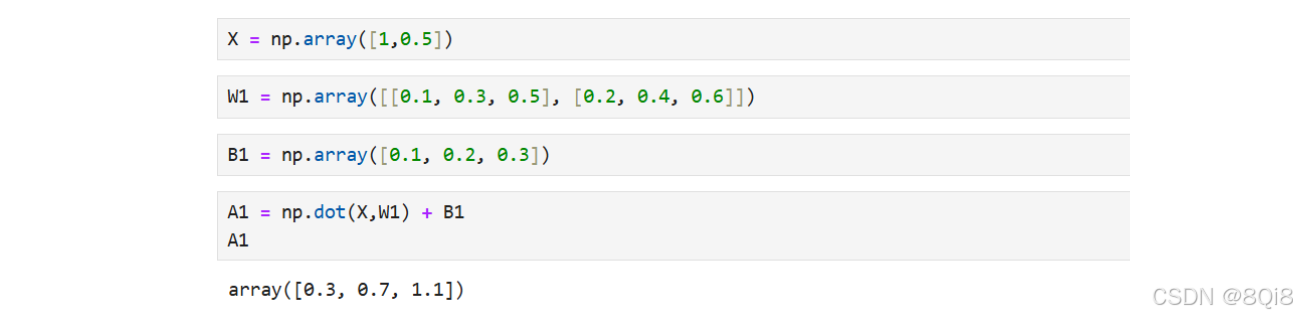
接下来，我们观察第1层中激活函数的计算过程：

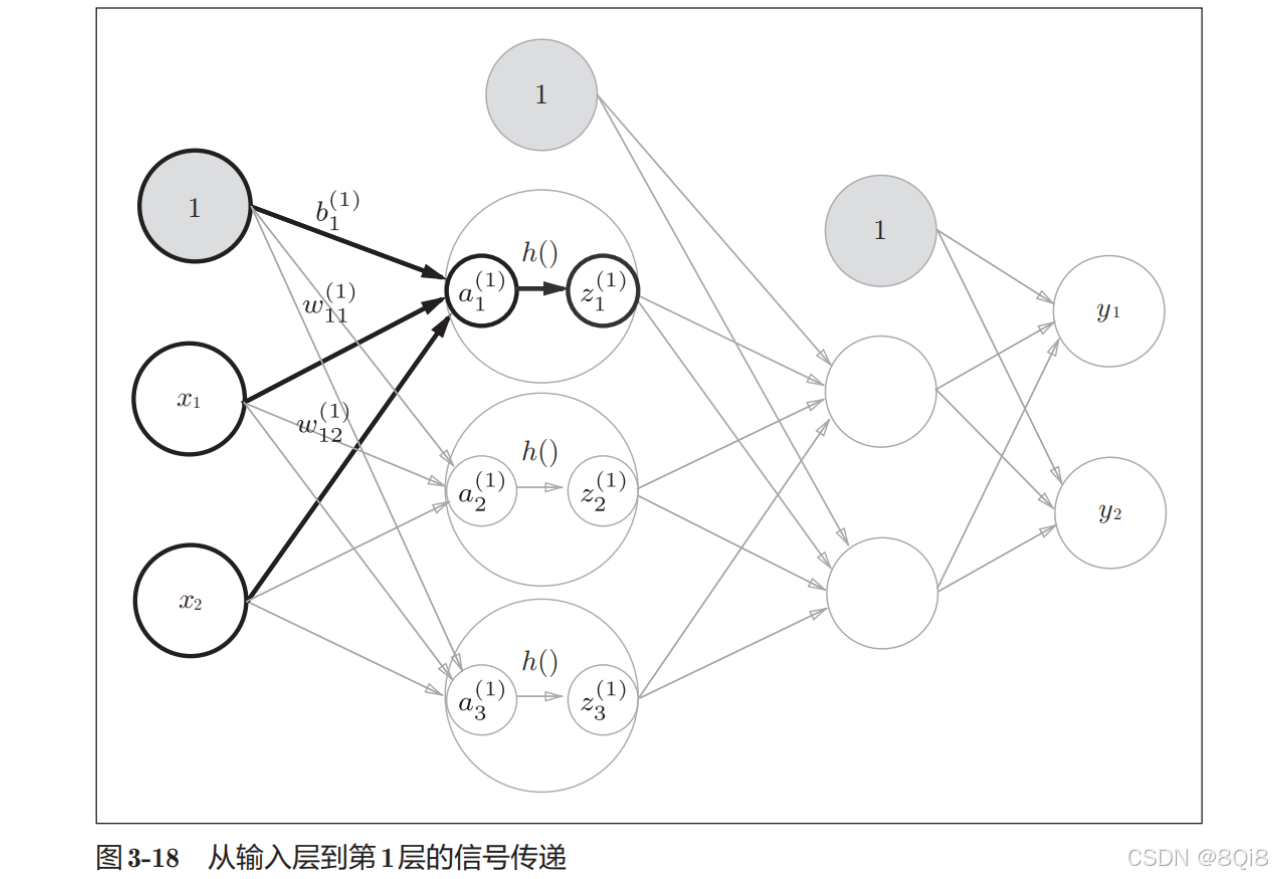
隐藏层的加权和（加权信号和偏置的总和）用a表示，被激活函数转换后的信号用z表示。此外，图中h()表示激活函数，这里我们使用的是sigmoid函数。

Z1 = sigmoid(A1)
print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.57444252, 0.66818777, 0.75026011]

接下来是第1层到第2层的信号传递：

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print(Z1.shape) # (3,)
print(W2.shape) # (3, 2)
print(B2.shape) # (2,)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

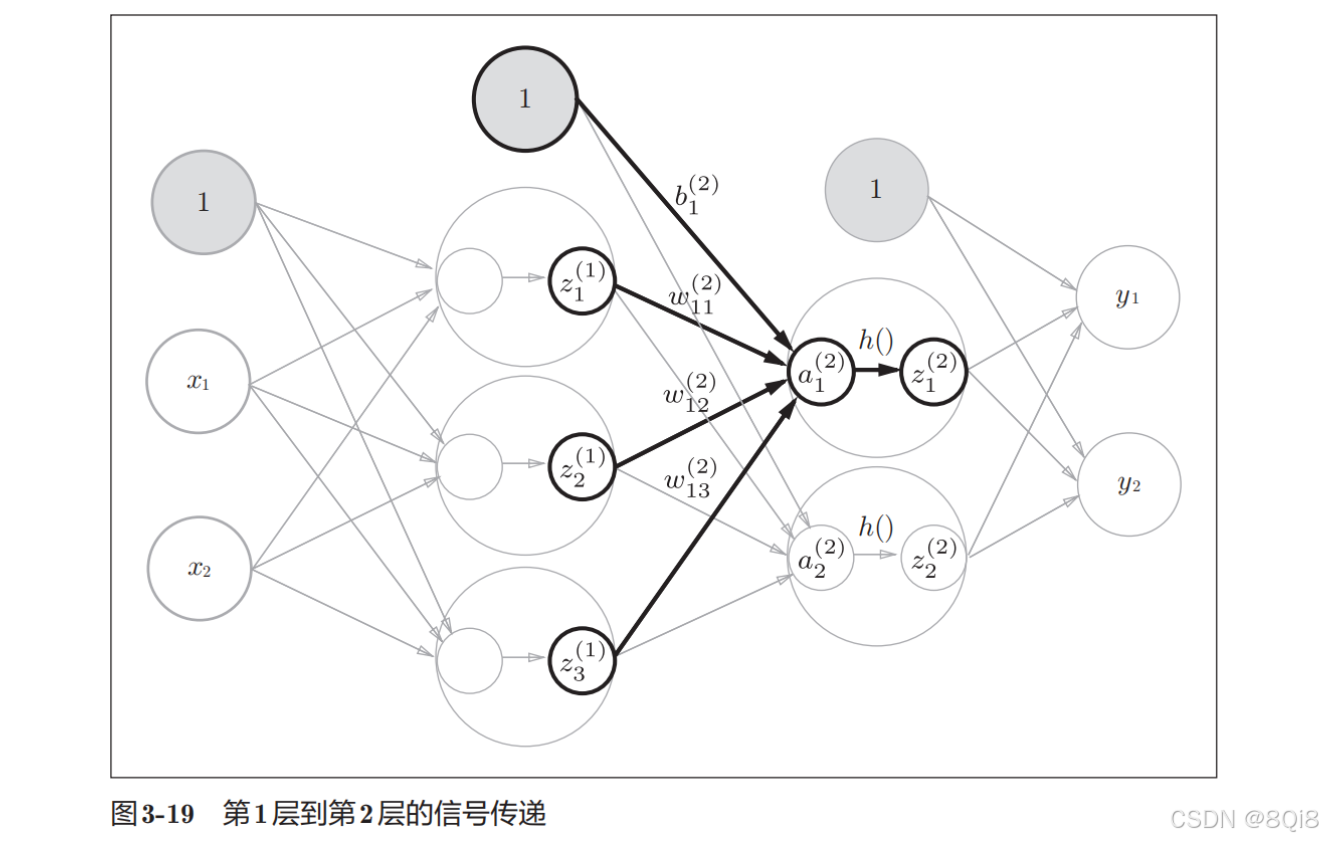
第2层到最后一层（输出层）的传递：

最后是第2层到输出层的信号传递。输出层的实现也和之前的实现基本相同。不过，最后的激活函数和之前的隐藏层有所不同。

# 恒等函数
def identity_function(x):
	return x

W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) # 或者Y = A3

恒等函数会将输入按原样输出，因此，这个例子中没有必要特意定义identity_function()。这里这样实现只是为了和之前的流程保持统一。另外，输出层的激活函数用σ()表示，不同于隐藏层的激活函数h()（σ读作sigma）。

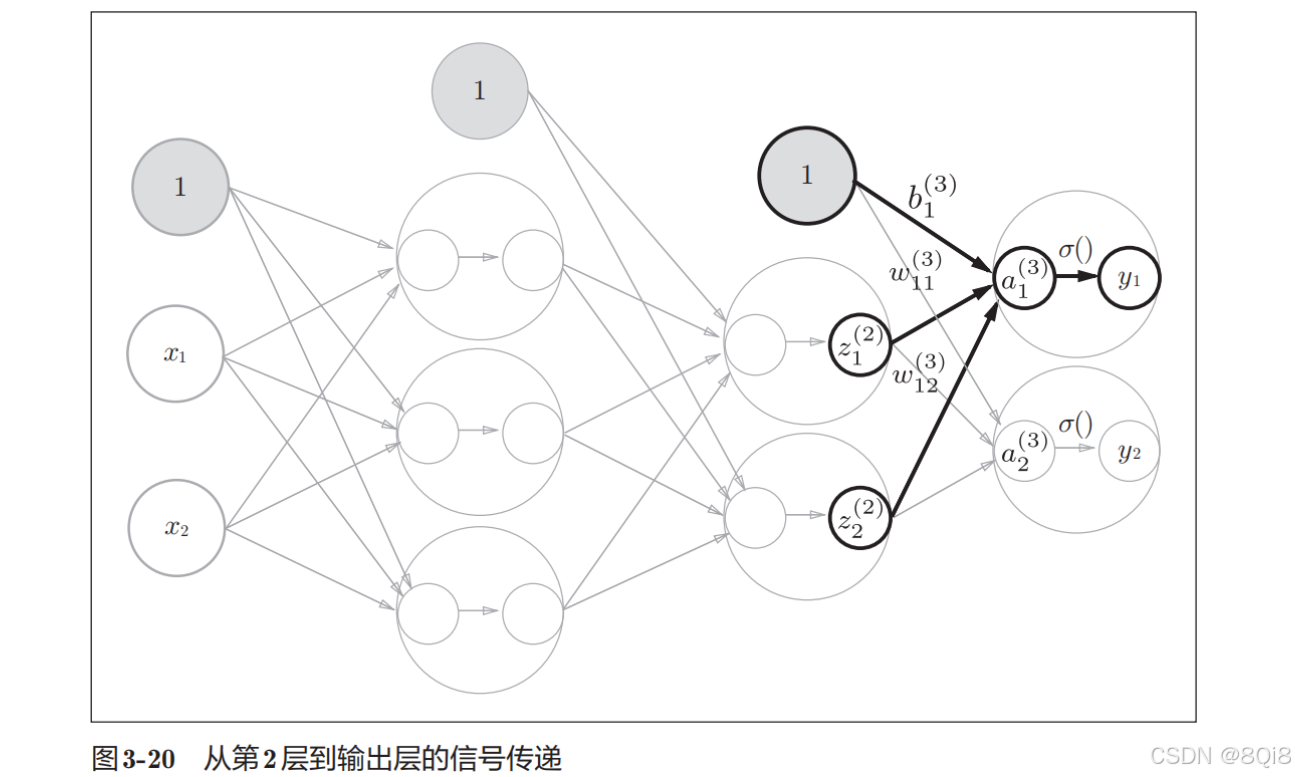
输出层所用的激活函数，要根据求解问题的性质决定。回归问题可以使用恒等函数，二元分类问题可以使用sigmoid函数，多元分类问题可以使用softmax函数。

3. 代码小结

   整理上述神经网络实现代码如下：

   def init_network():  # 初始化权重和参数
       network = {}
       network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
       network['b1'] = np.array([0.1, 0.2, 0.3])
       network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
       network['b2'] = np.array([0.1, 0.2])
       network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
       network['b3'] = np.array([0.1, 0.2])
       return network
   
   def forward(network,x):  # 前向传播
       W1,W2,W3 = network['W1'],network['W2'],network['W3']
       b1,b2,b3 = network['b1'],network['b2'],network['b3']
       a1 = np.dot(x,W1) + b1
       z1 = sigmoid(a1)
       a2 = np.dot(z1,W2) + b2
       z2 = sigmoid(a2)
       a3 = np.dot(z2,W3) + b3
       y = identity_function(a3)
       return y
   
   network = init_network()
   x = np.array([1,0.5])
   y = forward(network,x)
   y
   

二、输出层的设计

机器学习的问题大致可以分为分类问题和回归问题。

• 分类问题是数据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性的问题就是分类问题。

• 而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题（类似“57.4kg”这样的预测）。

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题用恒等函数，分类问题用softmax函数。

1. 恒等函数和softmax函数

   恒等函数会将输入按原样输出，对于输入的信息，不加以任何改动地直接输出。因此，在输出层使用恒等函数时，输入信号会原封不动地被输出。将恒等函数的处理过程用之前的神经网络图来表示的话，则如下图所示：

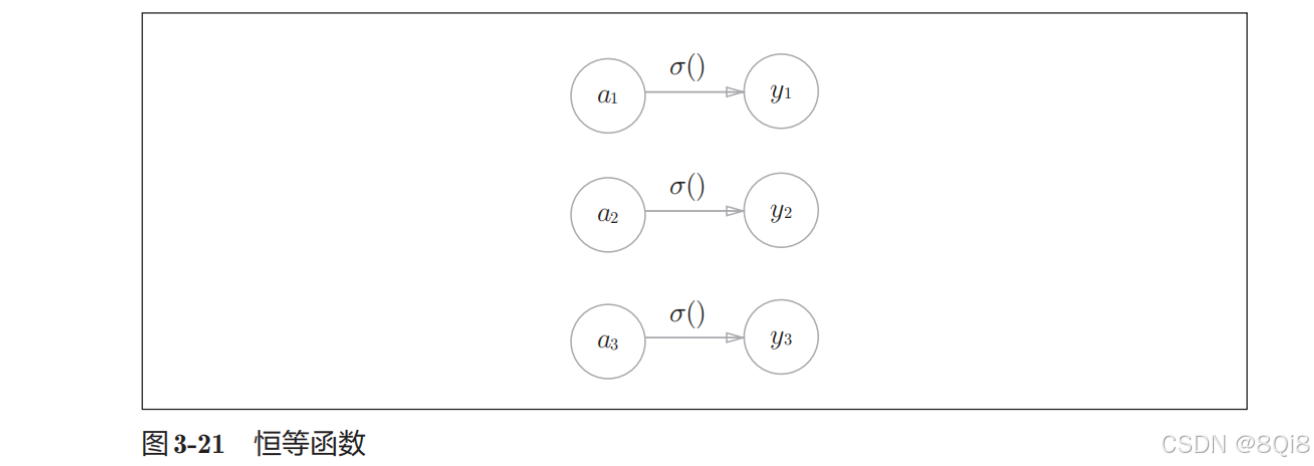
分类问题中使用的softmax函数可以用下式所示：
$$y_k=\frac{\exp (a_k)}{{\sum }_{i=1}^n\exp (a_i)}$$
表示假设输出层共有n个神经元，计算第k个神经元的输出yk。softmax函数的分子是输入信号ak的指数函数，分母是所有输入信号的指数函数的和。

用图表示softmax函数的话，如图所示，softmax函数的输出通过箭头与所有的输入信号相连。这是因为，输出层的各个神经元都受到所有输入信号的影响。

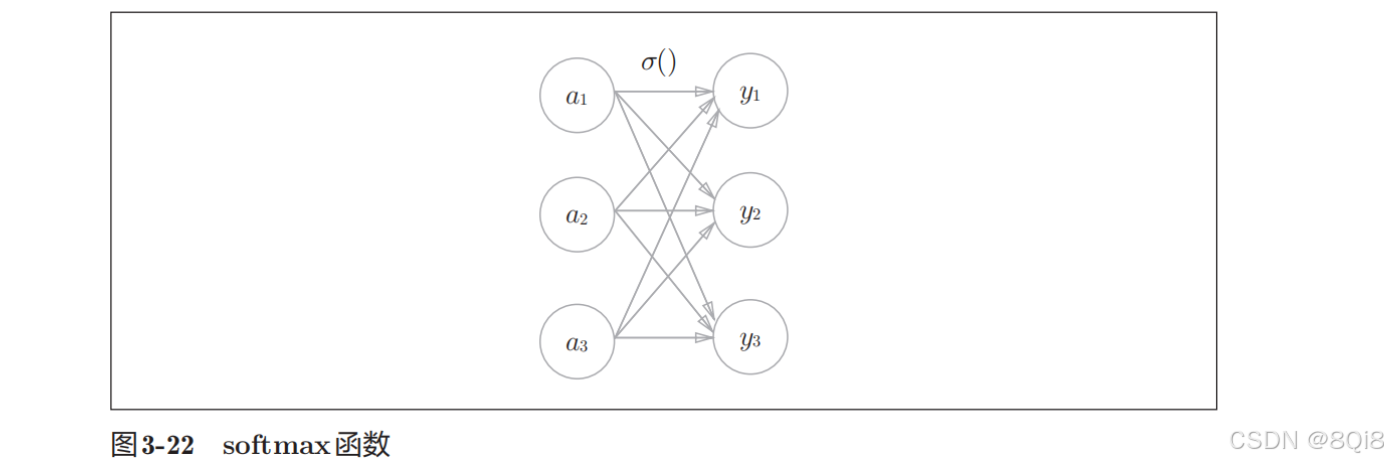
softmax函数实现：

a = np.array([0.3, 2.9, 4.0])
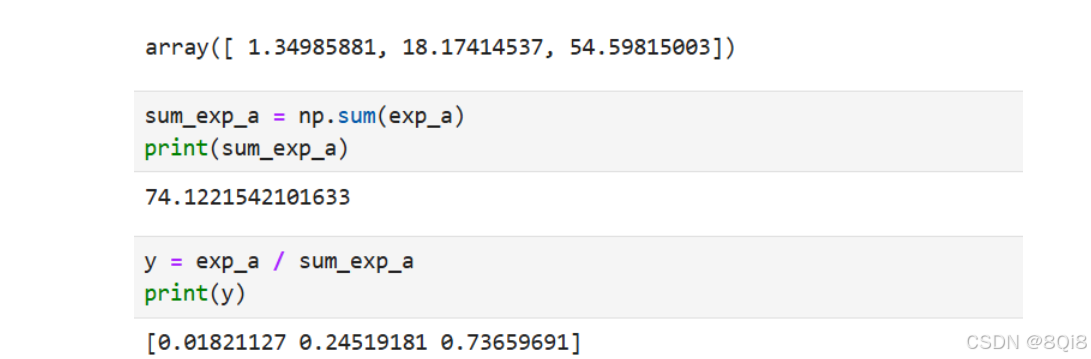
exp_a = np.exp(a)
exp_a
sum_exp_a = np.sum(exp_a)
print(sum_exp_a)
y = exp_a / sum_exp_a
print(y)

# 定义成函数
def softmax(a):
	exp_a = np.exp(a)
	sum_exp_a = np.sum(exp_a)
	y = exp_a / sum_exp_a
    return y

2. 实现softmax函数时的注意事项

   计算机的运算上有一定的缺陷。这个缺陷就是溢出问题。softmax函数的实现中要进行指数函数的运算，但是此时指数函数的值很容易变得非常大。$e^{10}$的值会超过20000，$e^{100}$会变成一个后面有40多个0的超大值，$e^{1000}$的结果会返回一个表示无穷大的inf。如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况。

   softmax函数的实现可以像下式这样进行改进。
   $$\begin{array}{rl}{y}_k& =\frac{\exp (a_k)}{{\sum }_{i=1}^n\exp (a_i)}=\frac{C\exp (a_k)}{C{\sum }_{i=1}^n\exp (a_i)}\\ & =\frac{\exp (a_k+\log C)}{{\sum }_{i=1}^n\exp (a_i+\log C)}\\ & =\frac{\exp (a_k+C^{\prime })}{{\sum }_{i=1}^n\exp (a_i+C^{\prime })}\end{array}$$
   首先，在分子和分母上都乘上C这个任意的常数。然后，把这个C移动到指数函数（exp）中，记为log C。最后，把log C替换为另一个符号C‘ 。这里的C’ 可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。

   例子：

   a = np.array([1010, 1000, 990])
   exp_a = np.exp(a)
   print(exp_a)
   np.exp(a) / np.sum(np.exp(a))
   

c = np.max(a)
print(a-c)
print(np.exp(a-c) / np.sum(np.exp(a-c)))

修改后的softmax函数：

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

3. softmax函数的特征
   

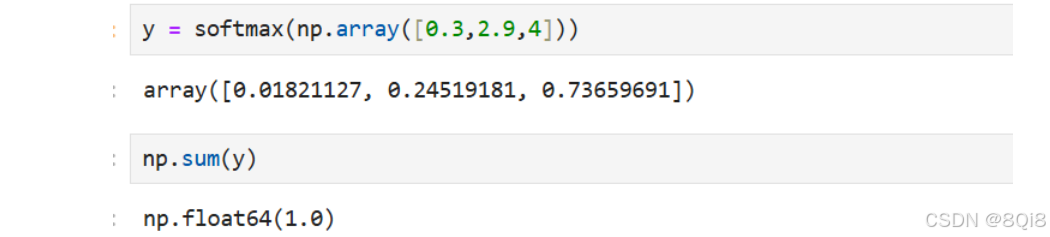
   如上所示，softmax函数的输出是0.0到1.0之间的实数。并且，softmax函数的输出值的总和是1。正因为有了这个性质，我们才可以把softmax函数的输出解释为“概率”。

   上面的例子可以解释成y[0]的概率是0.018（1.8 %），y[1]的概率是0.245（24.5 %），y[2]的概率是0.737（73.7 %）。也就是说，通过使用softmax函数，我们可以用概率的（统计的）方法处理问题。

   注意：即便使用了softmax函数，各个元素之间的大小关系也不会改变。因为指数函数**（y = exp(x)）是单调递增函数**。

• 一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果。即便使用softmax函数，输出值最大的神经元的位置也不会变。因此，神经网络在进行分类时，输出层的softmax函数可以省略。在实际的问题中，由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数一般会被省略。
• 求解机器学习问题的步骤可以分为**“学习”和“推理”**两个阶段。首先，在学习阶段进行模型的学习，然后，在推理阶段，用学到的模型对未知的数据进行推理（分类），推理阶段一般会省略输出层的 softmax函数。

4. 输出层的神经元数量

   对于分类问题，输出层的神经元数量一般设定为类别的数量。比如，对于某个输入图像，预测是图中的数字0到9中的哪一个的问题（10类别分类问题），可以像下图这样，将输出层的神经元设定为10个。其中，神经元y2颜色最深，输出的值最大。这表明这个神经网络预测的是y2对应的类别，也就是“2”。