0 专栏介绍
🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
🚀详情:运动规划实战进阶:轨迹优化篇
1 连续系统离散化
定义在时域的连续时间系统方程为
{ x ˙ ( t ) = A x ( t ) + B u ( t ) y ( t ) = C x ( t ) + D u ( t ) \begin{cases} \dot{\boldsymbol{x}}(t) = \boldsymbol{A}\boldsymbol{x}(t) + \boldsymbol{B}\boldsymbol{u}(t) \\ \boldsymbol{y}(t) = \boldsymbol{C}\boldsymbol{x}(t) + \boldsymbol{D}\boldsymbol{u}(t) \end{cases} {x˙(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)
经过 z z z变换后可得 z z z 域系统方程及传递函数:
{ z X ( z ) = A d X ( z ) + B d U ( z ) Y ( z ) = C d X ( z ) + D d U ( z ) ⟹ G ( z ) = C d ( z I − A d ) − 1 B d + D d \begin{cases} z\boldsymbol{X}(z) = \boldsymbol{A}_d\boldsymbol{X}(z) + \boldsymbol{B}_d\boldsymbol{U}(z) \\ \boldsymbol{Y}(z) = \boldsymbol{C}_d\boldsymbol{X}(z) + \boldsymbol{D}_d\boldsymbol{U}(z) \end{cases} \implies G(z) = \boldsymbol{C}_d(z\boldsymbol{I} - \boldsymbol{A}_d)^{-1}\boldsymbol{B}_d + \boldsymbol{D}_d {zX(z)=AdX(z)+BdU(z)Y(z)=CdX(z)+DdU(z)⟹G(z)=Cd(zI−Ad)−1Bd+Dd
连续系统离散化的核心在于用差分方法估计连续系统的微分量 x ˙ ( t ) \dot{\boldsymbol{x}}(t) x˙(t),并建立离散状态矩阵与连续矩阵的关系。不妨将对微分 x ˙ ( t ) \dot{\boldsymbol{x}}(t) x˙(t)的估计问题转变为对积分
x ( t ) = ∫ x ˙ ( t ) \boldsymbol{x}(t) = \int \dot{\boldsymbol{x}}(t) x(t)=∫x˙(t)
的估计问题, x ( t ) \boldsymbol{x}(t) x(t)的物理意义是从初始时刻到 t t t时刻 x ˙ ( t ) \dot{\boldsymbol{x}}(t) x˙(t)的积分值—— x ˙ ( t ) \dot{\boldsymbol{x}}(t) x˙(t)曲线下方的面积。接下来,基于上述概念推导常用的连续系统离散化方法。
2 欧拉法
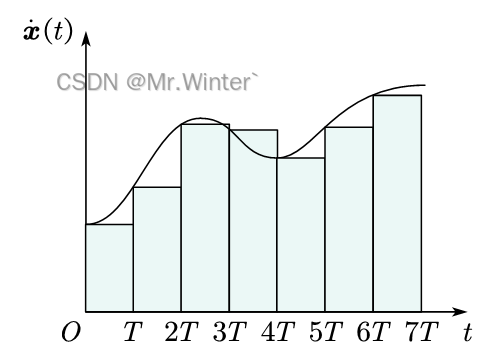
如图所示,采用左端点矩形近似 x ( t ) \boldsymbol{x}(t) x(t),则 x ( k T + T ) = x ( k T ) + x ˙ ( k T ) ⋅ T \boldsymbol{x}(kT + T) = \boldsymbol{x}(kT) + \dot{\boldsymbol{x}}(kT) \cdot T x(kT+T)=x(kT)+x˙(kT)⋅T,对方程两边应用 z z z变换和Laplace变换有:
z X ( z ) = X ( z ) + s T X ( s ) z\boldsymbol{X}(z) = \boldsymbol{X}(z) + sT\boldsymbol{X}(s) zX(z)=X(z)+sTX(s)
令 X ( s ) = X ( z ) X(s) = X(z) X(s)=X(z)(即频域映射关系),即得欧拉法的映射:
s = z − 1 T s = \frac{z - 1}{T} s=Tz−1
将该式代入连续系统方程,使连续系统映射到离散系统:
G d ( z ) = C ( z − 1 T I − A ) − 1 B + D ⇒ G d ( z ) = C ( z I − ( I + T A ) ) − 1 B T + D \boldsymbol{G}_d(z) = \boldsymbol{C}\left( \frac{z - 1}{T} \boldsymbol{I} - \boldsymbol{A} \right)^{-1} \boldsymbol{B} + \boldsymbol{D} \Rightarrow \boldsymbol{G}_d(z) = \boldsymbol{C}(z \boldsymbol{I} - (\boldsymbol{I} + T \boldsymbol{A}))^{-1} \boldsymbol{B} T + \boldsymbol{D} Gd(z)=C(Tz−1I−A)−1B+D⇒Gd(z)=C(zI−(I+TA))−1BT+D
对比离散系统标准形式,即得欧拉法离散化公式:
A d = I + T A , B d = B T , C d = C , D d = D \boldsymbol{A}_d = \boldsymbol{I} + T \boldsymbol{A}, \quad \boldsymbol{B}_d = B T, \quad \boldsymbol{C}_d = \boldsymbol{C}, \quad \boldsymbol{D}_d = \boldsymbol{D} Ad=I+TA,Bd=BT,Cd=C,Dd=D
以及离散化差分方程:
x ( k + 1 ) = ( I + T A ) x ( k ) + B T u ( k ) y ( k ) = C x ( k ) + D u ( k ) \begin{matrix} \boldsymbol{x}(k+1) = (\boldsymbol{I} + T \boldsymbol{A}) \boldsymbol{x}(k) + B T \boldsymbol{u}(k) \\ \boldsymbol{y}(k) = \boldsymbol{C} \boldsymbol{x}(k) + D \boldsymbol{u}(k) \end{matrix} x(k+1)=(I+TA)x(k)+BTu(k)y(k)=Cx(k)+Du(k)
根据泰勒展开:
x ( t + T ) = x ( t ) + T x ˙ ( t ) + 1 2 T 2 x ¨ ( t ) + ⋯ \boldsymbol{x}(t+T) = \boldsymbol{x}(t) + T \dot{\boldsymbol{x}}(t) + \frac{1}{2} T^2 \ddot{\boldsymbol{x}}(t) + \cdots x(t+T)=x(t)+Tx˙(t)+21T2x¨(t)+⋯
可知,欧拉法近似误差为采样周期的一阶精度:
x ( t + T ) − x ( t ) T − x ˙ ( t ) ≈ 1 2 T x ¨ ( t ) = O ( T ) \frac{\boldsymbol{x}(t+T) - \boldsymbol{x}(t)}{T} - \dot{\boldsymbol{x}}(t) \approx \frac{1}{2} T \ddot{\boldsymbol{x}}(t) = O(T) Tx(t+T)−x(t)−x˙(t)≈21Tx¨(t)=O(T)
3 双线性变换

如图所示, 采用梯形近似 x ( t ) \boldsymbol{x}(t) x(t), 则
x ( k T + T ) = x ( k T ) + T 2 ( x ^ ( k T ) + x ( k T + T ) ) \boldsymbol{x}(k T+T)=\boldsymbol{x}(k T)+\frac{T}{2}(\hat{\boldsymbol{x}}(k T)+\boldsymbol{x}(k T+T)) x(kT+T)=x(kT)+2T(x^(kT)+x(kT+T))
对方程两边应用 z z z变换和Laplace 变换有
2 z X ( z ) = 2 X ( z ) + T ( s X ( s ) + s z X ( s ) ) 2 z \boldsymbol{X}(z)=2 \boldsymbol{X}(z)+T(s \boldsymbol{X}(s)+s z \boldsymbol{X}(s)) 2zX(z)=2X(z)+T(sX(s)+szX(s))
令 X ( s ) = X ( z ) \boldsymbol{X}(s)=\boldsymbol{X}(z) X(s)=X(z)即得双线性变换映射
s = 2 ( z − 1 ) T ( z + 1 ) s=\frac{2(z-1)}{T(z+1)} s=T(z+1)2(z−1)
将该式代入 (8.2) 使连续系统映射到离散系统
G d ( z ) = C ( z I − ( I − 1 2 T A ) − 1 ( I + 1 2 T A ) ) − 1 1 2 ( I − 1 2 T A ) − 1 B T ( z + 1 ) + D \boldsymbol{G}_{d}(z)=\boldsymbol{C}\left(z \boldsymbol{I}-\left(\boldsymbol{I}-\frac{1}{2} T \boldsymbol{A}\right)^{-1}\left(\boldsymbol{I}+\frac{1}{2} T \boldsymbol{A}\right)\right)^{-1} \frac{1}{2}\left(\boldsymbol{I}-\frac{1}{2} T \boldsymbol{A}\right)^{-1} \boldsymbol{B} T(z+1)+\boldsymbol{D} Gd(z)=C(zI−(I−21TA)−1(I+21TA))−121(I−21TA)−1BT(z+1)+D
进一步得到
A d = ( I − 1 2 T A ) − 1 ( I + 1 2 T A ) B d = 1 2 ( I − 1 2 T A ) − 1 B T C d = C ( I + ( I − T 2 A ) − 1 ( I + T 2 A ) ) D d = D + C B T 2 ( I − T 2 A ) − 1 A_{d}=\left(I - \frac{1}{2}TA\right)^{-1}\left(I + \frac{1}{2}TA\right) \\ B_{d}=\frac{1}{2}\left(I - \frac{1}{2}TA\right)^{-1}BT \\ C_{d}=C\left(I+\left(I - \frac{T}{2}A\right)^{-1}\left(I + \frac{T}{2}A\right)\right) \\ D_{d}=D+\frac{CBT}{2}\left(I - \frac{T}{2}A\right)^{-1} Ad=(I−21TA)−1(I+21TA)Bd=21(I−21TA)−1BTCd=C(I+(I−2TA)−1(I+2TA))Dd=D+2CBT(I−2TA)−1
和离散化差分方程组
{ x ( k + 1 ) = ( I − T 2 A ) − 1 ( I + T 2 A ) x ( k ) + B T 2 ( I − T 2 A ) − 1 u ( k ) y ( k ) = C ( I + ( I − T 2 A ) − 1 ( I + T 2 A ) ) x ( k ) + ( D + C B T 2 ( I − T 2 A ) − 1 ) u ( k ) \begin{cases} x(k + 1)=\left(I - \frac{T}{2}A\right)^{-1}\left(I + \frac{T}{2}A\right)x(k)+\frac{BT}{2}\left(I - \frac{T}{2}A\right)^{-1}u(k)\\ y(k)=C\left(I+\left(I - \frac{T}{2}A\right)^{-1}\left(I + \frac{T}{2}A\right)\right)x(k)+\left(D+\frac{CBT}{2}\left(I - \frac{T}{2}A\right)^{-1}\right)u(k) \end{cases} {x(k+1)=(I−2TA)−1(I+2TA)x(k)+2BT(I−2TA)−1u(k)y(k)=C(I+(I−2TA)−1(I+2TA))x(k)+(D+2CBT(I−2TA)−1)u(k)
基于泰勒展开的公式:
x ( t + T ) − x ( t ) T = x ˙ ( t ) + 1 2 T x ¨ ( t ) + 1 6 T 2 x ¨ ( t ) + ⋯ \frac{\boldsymbol{x}(t + T)-\boldsymbol{x}(t)}{T}=\dot{\boldsymbol{x}}(t)+\frac{1}{2}T\ddot{\boldsymbol{x}}(t)+\frac{1}{6}T^{2}\ddot{\boldsymbol{x}}(t)+\cdots Tx(t+T)−x(t)=x˙(t)+21Tx¨(t)+61T2x¨(t)+⋯
对比双线性变换公式:
x ( t + T ) − x ( t ) T = 1 2 ( x ˙ ( t ) + x ˙ ( t + T ) ) = 1 2 x ˙ ( t ) + 1 2 ( x ˙ ( t ) + T x ¨ ( t ) + 1 2 T 2 x ¨ ( t ) + ⋯ ) = x ˙ ( t ) + 1 2 T x ¨ ( t ) + 1 4 T 2 x ¨ ( t ) + ⋯ \begin{align*} \frac{\boldsymbol{x}(t + T)-\boldsymbol{x}(t)}{T}&=\frac{1}{2}(\dot{\boldsymbol{x}}(t)+\dot{\boldsymbol{x}}(t + T))\\ &=\frac{1}{2}\dot{\boldsymbol{x}}(t)+\frac{1}{2}\left(\dot{\boldsymbol{x}}(t)+T\ddot{\boldsymbol{x}}(t)+\frac{1}{2}T^{2}\ddot{\boldsymbol{x}}(t)+\cdots\right)\\ &=\dot{\boldsymbol{x}}(t)+\frac{1}{2}T\ddot{\boldsymbol{x}}(t)+\frac{1}{4}T^{2}\ddot{\boldsymbol{x}}(t)+\cdots \end{align*} Tx(t+T)−x(t)=21(x˙(t)+x˙(t+T))=21x˙(t)+21(x˙(t)+Tx¨(t)+21T2x¨(t)+⋯)=x˙(t)+21Tx¨(t)+41T2x¨(t)+⋯
可得双线性变换近似误差为采样周期的二阶精度 O ( T 2 ) O(T^{2}) O(T2)。
4 龙格库塔法
由拉格朗日中值定理,若函数 f ( x ) f(x) f(x) 满足在闭区间 [ a , b ] [a, b] [a,b]上连续,在开区间 ( a , b ) (a, b) (a,b) 上可导,则在 ( a , b ) (a, b) (a,b)上至少存在一点 ξ \xi ξ 使等式 f ( b ) − f ( a ) = f ′ ( ξ ) ( b − a ) f(b) - f(a) = f'(\xi)(b - a) f(b)−f(a)=f′(ξ)(b−a) 成立。
因此, x ( k T + T ) \boldsymbol{x}(kT + T) x(kT+T) 的准确解为 x ( k T + T ) = x ( k T ) + x ˙ ( ξ ) T \boldsymbol{x}(kT + T) = \boldsymbol{x}(kT) + \dot{\boldsymbol{x}}(\xi)T x(kT+T)=x(kT)+x˙(ξ)T。前向差分法和后向差分法相当于分别用区间端点的斜率近似,即 x ˙ ( ξ ) = x ˙ ( k T ) \dot{\boldsymbol{x}}(\xi) = \dot{\boldsymbol{x}}(kT) x˙(ξ)=x˙(kT) 与 x ˙ ( ξ ) = x ˙ ( k T + T ) \dot{\boldsymbol{x}}(\xi) = \dot{\boldsymbol{x}}(kT + T) x˙(ξ)=x˙(kT+T),显然不够准确。基于此,龙格库塔法的核心思想是通过区间多点采样逼近 x ˙ ( ξ ) \dot{\boldsymbol{x}}(\xi) x˙(ξ) 实现更精确的离散化估计,其中采样点数定义为龙格库塔法的阶数。欧拉法可视为一阶龙格库塔法。
一般地,令 x ˙ ( t ) = f ( x , t ) \dot{\boldsymbol{x}}(t) = f(\boldsymbol{x}, t) x˙(t)=f(x,t), x ( k T ) = x k \boldsymbol{x}(kT) = \boldsymbol{x}_k x(kT)=xk, k T = t k kT = t_k kT=tk ,则泰勒展开
x k + 1 = x k + T x ˙ k + 1 2 T 2 x ¨ k + O ( T 3 ) \boldsymbol{x}_{k+1} = \boldsymbol{x}_k + T\dot{\boldsymbol{x}}_k + \frac{1}{2}T^2\ddot{\boldsymbol{x}}_k + O(T^3) xk+1=xk+Tx˙k+21T2x¨k+O(T3)
其中 x ¨ ( t ) = d f ( x , t ) / d t = f t ( x , t ) + f ( x , t ) ⋅ f x ( x , t ) ⇒ x ¨ k = f t ( x k , t k ) + f ( x k , t k ) ⋅ f x ( x k , t k ) \ddot{\boldsymbol{x}}(t) = \mathrm{d}f(\boldsymbol{x}, t)/\mathrm{d}t = f_t(\boldsymbol{x}, t) + f(\boldsymbol{x}, t) \cdot f_{\boldsymbol{x}}(\boldsymbol{x}, t) \Rightarrow \ddot{\boldsymbol{x}}_k = f_t(\boldsymbol{x}_k, t_k) + f(\boldsymbol{x}_k, t_k) \cdot f_{\boldsymbol{x}}(\boldsymbol{x}_k, t_k) x¨(t)=df(x,t)/dt=ft(x,t)+f(x,t)⋅fx(x,t)⇒x¨k=ft(xk,tk)+f(xk,tk)⋅fx(xk,tk)。代入上式可得
x k + 1 = x k + T f + 1 2 T 2 ( f t + f f x ) + O ( T 3 ) \boldsymbol{x}_{k+1} = \boldsymbol{x}_k + Tf + \frac{1}{2}T^2(f_t + ff_{\boldsymbol{x}}) + O(T^3) xk+1=xk+Tf+21T2(ft+ffx)+O(T3)
二阶龙格库塔法在区间 [ t k , t k + 1 ] [t_k, t_{k+1}] [tk,tk+1]上采样两个点,分别记为
{ k 1 = f ( x k , t k ) k 2 = f ( x k + c 1 k 1 T , t k + c 2 T ) ⟹ x k + 1 = x k + ( λ 1 k 1 + λ 2 k 2 ) T \begin{cases} k_1 = f(x_k, t_k) \\ k_2 = f(x_k + c_1 k_1 T, t_k + c_2 T) \end{cases} \implies x_{k+1} = x_k + (\lambda_1 k_1 + \lambda_2 k_2) T {k1=f(xk,tk)k2=f(xk+c1k1T,tk+c2T)⟹xk+1=xk+(λ1k1+λ2k2)T
其中 λ i \lambda_i λi与 c i c_i ci均为待定系数。对 k 2 k_2 k2一阶泰勒展开有:
k 2 = f ( x k + c 1 k 1 T , t k + c 2 T ) = f + c 2 T f t + c 1 T f x + O ( T 3 ) k_2 = f(x_k + c_1 k_1 T, t_k + c_2 T) = f + c_2 T f_t + c_1 T f_{x} + \mathrm{O}(T^3) k2=f(xk+c1k1T,tk+c2T)=f+c2Tft+c1Tfx+O(T3)
将 k 1 k_1 k1和 k 2 k_2 k2代入 x k + 1 x_{k+1} xk+1可得:
x k + 1 = x k + ( λ 1 + λ 2 ) T f + T 2 2 ( 2 λ 2 c 2 f t + 2 c 1 λ 2 f x x ) + O ( T 3 ) x_{k+1} = x_k + (\lambda_1 + \lambda_2) T f + \frac{T^2}{2} \left( 2 \lambda_2 c_2 f_t + 2 c_1 \lambda_2 f_{xx} \right) + \mathrm{O}(T^3) xk+1=xk+(λ1+λ2)Tf+2T2(2λ2c2ft+2c1λ2fxx)+O(T3)
对比系数可知:
{ λ 1 + λ 2 = 1 λ 2 c 1 = λ 2 c 2 = 1 2 \begin{cases} \lambda_1 + \lambda_2 = 1 \\ \lambda_2 c_1 = \lambda_2 c_2 = \frac{1}{2} \end{cases} {λ1+λ2=1λ2c1=λ2c2=21
这个不定方程的一组可行解为 λ 1 = λ 2 = 1 / 2 , c 1 = c 2 = 1 \lambda_1 = \lambda_2 = 1/2,c_1 = c_2 = 1 λ1=λ2=1/2,c1=c2=1,所以二阶龙格库塔法表述为:
x k + 1 = x k + ( 1 2 k 1 + 1 2 k 2 ) T , { k 1 = f ( x k , t k ) k 2 = f ( x k + T , t k + 1 ) x_{k+1} = x_k + \left( \frac{1}{2} k_1 + \frac{1}{2} k_2 \right) T, \quad \begin{cases} k_1 = f(x_k, t_k) \\ k_2 = f(x_k + T, t_k + 1) \end{cases} xk+1=xk+(21k1+21k2)T,{k1=f(xk,tk)k2=f(xk+T,tk+1)
二阶龙格库塔法也称为改进欧拉法。依次类推,可以得到高阶龙格库塔法公式。四阶龙格库塔法达到了精度和效率的最佳平衡,因此工程中应用最广泛。接下来推导基于状态方程的四阶龙格库塔法积分。假定状态方程时不变,则
x k + 1 = x k + T 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) , { k 1 = f ( x k , u k ) k 2 = f ( x k + k 1 2 T , u k ) k 3 = f ( x k + k 2 2 T , u k ) k 4 = f ( x k + k 3 T , u k ) \boldsymbol{x}_{k+1}=\boldsymbol{x}_k+\frac{T}{6}\left( \boldsymbol{k}_1+2\boldsymbol{k}_2+2\boldsymbol{k}_3+\boldsymbol{k}_4 \right) , \begin{cases} \boldsymbol{k}_1=\boldsymbol{f}\left( \boldsymbol{x}_k, \boldsymbol{u}_k \right)\\ \boldsymbol{k}_2=f\left( \boldsymbol{x}_k+\frac{\boldsymbol{k}_1}{2}T, \boldsymbol{u}_k \right)\\ \boldsymbol{k}_3=f\left( \boldsymbol{x}_k+\frac{\boldsymbol{k}_2}{2}T, \boldsymbol{u}_k \right)\\ \boldsymbol{k}_4=f\left( \boldsymbol{x}_k+\boldsymbol{k}_3T, \boldsymbol{u}_k \right)\\\end{cases} xk+1=xk+6T(k1+2k2+2k3+k4),⎩ ⎨ ⎧k1=f(xk,uk)k2=f(xk+2k1T,uk)k3=f(xk+2k2T,uk)k4=f(xk+k3T,uk)
5 Python实验
定义微分方程
y ′ = f ( x , y ) = − 0.9 y 1 + 2 x y'= f(x, y) = -\frac{0.9 y}{1 + 2x} y′=f(x,y)=−1+2x0.9y
其解析解为
y exact ( x ) = ( 1 + 2 x ) − 0.45 y_{\text{exact}}(x) = (1 + 2x)^{-0.45} yexact(x)=(1+2x)−0.45
欧拉法实现
def euler(f, x0, y0, h, n): x = np.zeros(n + 1) y = np.zeros(n + 1) x[0], y[0] = x0, y0 for i in range(n): y[i + 1] = y[i] + h * f(x[i], y[i]) x[i + 1] = x[i] + h return x, y改进欧拉法实现
def rk2(f, x0, y0, h, n): x = np.zeros(n + 1) y = np.zeros(n + 1) x[0], y[0] = x0, y0 for i in range(n): k1 = f(x[i], y[i]) k2 = f(x[i] + h, y[i] + h * k1) y[i + 1] = y[i] + h * (k1 + k2) / 2 x[i + 1] = x[i] + h return x, y三阶龙格库塔法
def rk3(f, x0, y0, h, n): x = np.zeros(n + 1) y = np.zeros(n + 1) x[0], y[0] = x0, y0 for i in range(n): k1 = f(x[i], y[i]) k2 = f(x[i] + h / 2, y[i] + h * k1 / 2) k3 = f(x[i] + h, y[i] - h * (k1 + 2 * k2)) y[i + 1] = y[i] + h * (k1 + 4 * k2 + k3) / 6 x[i + 1] = x[i] + h return x, y四阶龙格库塔法
def rk4(f, x0, y0, h, n): x = np.zeros(n + 1) y = np.zeros(n + 1) x[0], y[0] = x0, y0 for i in range(n): k1 = f(x[i], y[i]) k2 = f(x[i] + h / 2, y[i] + h * k1 / 2) k3 = f(x[i] + h / 2, y[i] + h * k2 / 2) k4 = f(x[i] + h, y[i] + h * k3) y[i + 1] = y[i] + h * (k1 + 2 * k2 + 2 * k3 + k4) / 6 x[i + 1] = x[i] + h return x, y
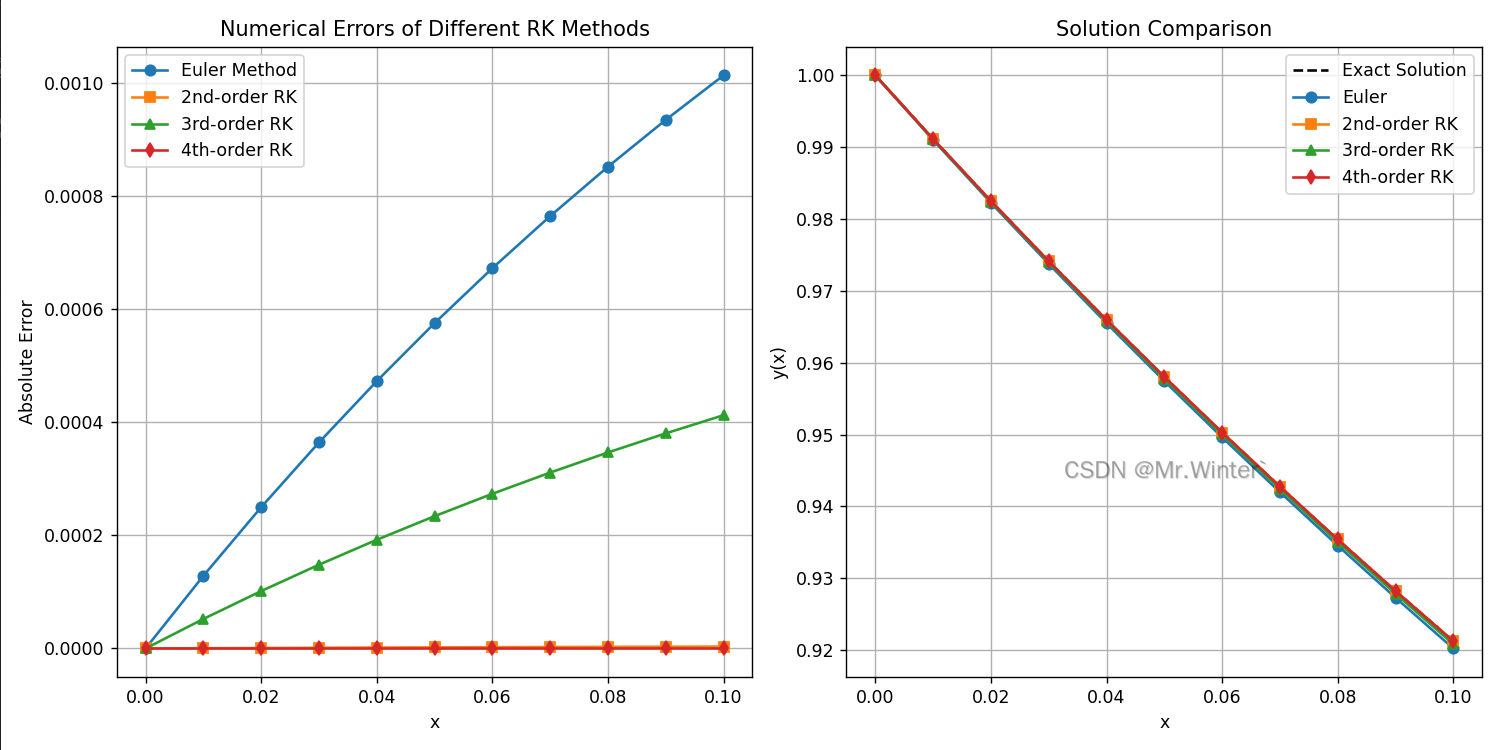
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏: