2025年最新中科院1区SCI-基尔霍夫定律优化算法Kirchhoff’s law algorithm-附完整Matlab免费代码

1、简介

本研究引入了基尔霍夫定律算法（KLA）是一种受电路定律，特别是基尔霍夫电流定律（KCL）启发的新型优化方法。本文首次开发了基尔霍夫定律算法（KLA）。KLA是一种熟练且有竞争力的优化技术，它借鉴了电路定律，即基尔霍夫电流定律（KCL）。在这方面，电路中的可变电阻由不同种群的成本目标函数建模。相比之下，节点电压和电压源分别由算法种群的位置和迭代次数建模。目标是最小化通过支路的电流流或减少由种群位移实现的功率损耗，即改变节点电压。将其结果与文献中关于各种优化问题算法的其他结果进行了比较，以确定所提出的KLA的关键方面。所提出的KLA在各种基准函数和实际优化问题上的性能表明，该算法能够解决广泛的优化问题，包括电力系统中的最佳资源调度、裂缝识别问题、通信问题、控制工程问题、医疗方面等。KLA是一种自由参数算法，可以采用不同的修改方法。KLA的引入可以说是优化领域以及封装设计、控制机制和工程领域许多其他领域的突破。作为嵌入在KLA中的物理激励算法，它为优化提供了一个新的视角，同时将纯粹的研究与应用联系起来。

2、基尔霍夫定律算法（KLA）

本节首先介绍了KLA的灵感来源，然后讨论了KLA中的数学模型和优化过程。它还讨论了所提出的KLA的潜在利弊。KLA源于电阻网络中电流的固有行为。在这种方法中，两个解之间的代价函数类似于电阻，每个潜在解都表示为抽象电路中的一个节点。基尔霍夫电流定律指出，进出节点的总电流是守恒的，电流有利于电阻降低的路径。
在优化的背景下，更好的（即更低的成本）解决方案对搜索轨迹产生更显著的影响。KLA利用这种相似性反复细化解决方案位置：类似电流的冲击将算法从一次迭代引导到随后的迭代，消除了控制参数的必要性。两个解决方案之间的电阻取决于它们的成本值，更新规则说明了实际电路中电流的流动——从高潜人才到低，有利于低电阻路径。这种物理并行有助于保持多样性，同时固有地促进向搜索空间的有利区域收敛。KLA利用基于物理定律的直观、自我调节的过程，与依赖于精心调整参数的典型算法形成鲜明对比。
该电压降由欧姆定律具体确定，并且是电路中最简单、或许也是最常用的元件之一——电阻器。简单来说，电阻器实现过程中所利用的电能效应与通过它的电流和电阻器本身直接成正比，并可根据欧姆定律用数学公式描述为$V=IR$。这种关系在电气工程中非常重要，因为它提供了一种简单的技术，用于在确定电阻器的电流和电阻时计算电压降。因此，欧姆定律极其简单且有效，可用于检查电路中各个阶段的电压和电流，使其成为电路分析和设计中不可或缺的工具。

$$V_R=I_R\times R（1）$$

其中，$V_R$是电阻两端的电压，$I_R$是通过电阻$R$的电流。这种关系被称为著名的欧姆定律，它表明每个电阻元件两端的电压与通过该元件的电流直接相关。
当所有系统元件均为线性时，所考虑的系统模型也将是线性的。如果一个元件满足叠加原理，则称其为线性元件。对于电阻$R$，叠加原理指出：对于给定电流$I_1$，电阻两端的电压为$V_1$；对于另一个给定电流$I_2$，电压为$V_2$。只有当电流为$(I_1+I_2)$时，电压等于$(V_1+V_2)$，该电阻才是线性的。电路分析的目的是找到给定元件或支路中的电流，并确定元件或电路两点之间的电压或电位差。基尔霍夫电流定律（KCL）已被用于分析电路。KCL（如图1所示）用于本文提出的建模中，它指出流入给定节点（即$N!$）的所有电流的代数和为零。电路中的节点是多个元件的共同连接点。对于一个具有四个输入电流的节点$N!=A$，这四个电流的代数和为零，即${\sum }_{n=1}{I}_n=I_1+I_2+I_3-I_4=0$。此处，流入/流出的电流分别具有正/负符号。因此，需要指出的是，在我们的模型中，理想电压源不能并联连接，理想电流源也不能串联连接。

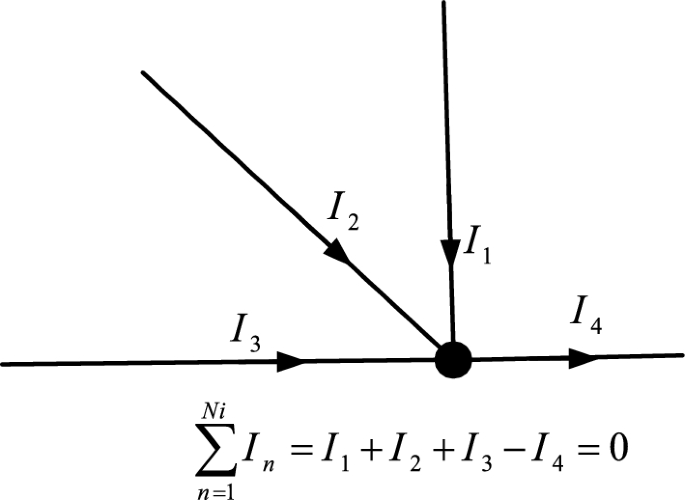
图1 基尔霍夫电流定律（KCL）：流入节点的所有电流的代数求和等于零
图2展示了一个电路中基尔霍夫电流定律（KCL）的通用示例，包括用于KLA的元件。考虑通过修改网络元件的特定参数来改变电流流动，从而降低网络损耗的可能性。例如，假设电压源的值被修改了ΔE，则可以计算出电流I1的新值，即$I_{new1}=I_1+\Delta I_1$。现在，对第一个节点（V1，绿色节点）应用KCL：

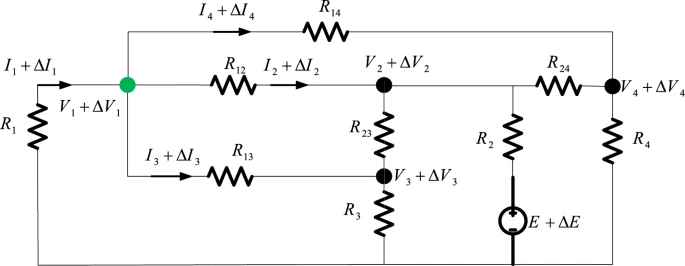
图2 用于算法目的的等效电路（示例1）
$$\{\begin{array}{c}{I}_1^{new}=I_1+\Delta I_1=I_2+\Delta I_2+I_3+\Delta I_3+I_4+\Delta I_4\\ \Delta I_1=\Delta I_2+\Delta I_3+\Delta I_4\\ I_1^{new}=I_2^{new}+I_3^{new}+I_4^{new}\end{array}$$
电压表述为
$$\{\begin{array}{c}{V}_1^{new}=V_1+\Delta V_1\\ V_2^{new}=V_2+\Delta V_2\\ V_3^{new}=V_3+\Delta V_3\\ V_4^{new}=V_4+\Delta V_4\end{array}$$
电流表述为
$$\{\begin{array}{c}{I}_2^{new}=\frac{\left(V_1^{new}-V_2^{new}\right)}{R_{12}}\\ I_3^{new}=\frac{\left(V_1^{new}-V_3^{new}\right)}{R_{13}}\\ I_4^{new}=\frac{\left(V_1^{new}-V_4^{new}\right)}{R_{14}}\\ I_1^{new}=I_2^{new}+I_3^{new}+I_4^{new}=\frac{\left(V_1^{new}-V_2^{new}\right)}{R_{12}}+\frac{\left(V_1^{new}-V_3^{new}\right)}{R_{13}}+\frac{\left(V_1^{new}-V_4^{new}\right)}{R_{14}}\end{array}$$
这些方程描述了电路中更新后的电流和电压值。值得注意的是，方程（4）展示了如何基于通过KCL计算得到的更新后电压$V_1^{new}$、$V_2^{new}$、$V_3^{new}$和$V_4^{new}$来计算$I_1^{new}$。这一过程能够推导出节点电压，从而为电路的分析和优化提供便利。总体而言，图2中电路配置的选择展示了KCL在KLA背景下的应用，为理解该算法的基础原理提供了帮助。优化算法已经从传统的线性规划类优化，逐渐发展为基于梯度的优化以及元启发式算法的兴起。这一领域的发展主要源于需要解决的实际问题的数量和难度，以及这些问题通常涉及对多个冲突标准和约束的优化。尽管一些早期技术对于简单问题完全可行，但在应用于更复杂的情况时可能缺乏可扩展性或鲁棒性。元启发式方法基于自然、物理世界和社会的原理应运而生，极大地推动了搜索算法的改进，提供了在更广阔和更复杂的解空间中进行搜索的方法。随着计算能力的不断提升，解决这些问题变得更加容易，进而催生了更优、更完善且更集成的优化方法。

2.1 KLA的基本概念

KLA利用电路分析的原理来优化现实世界的问题。在这种方法中，电路中的节点电压充当EA中种群或阵列的位置。这些节点电压之间的电阻被视为目标函数的变量函数。优化目标是通过调整节点电压来最小化能量损失，类似于找到最佳化问题的最佳解决方案。KLA基于KCL迭代更新节点电压，并将其与以前的解决方案相结合，以生成改进的种群。

为了阐明算法制定中选择电路架构背后的原因，必须强调所采用的建模方法。选择电路配置不是因为它的物理布置，而是因为它代表了基本的优化动态。每个电阻器表示两个候选解决方案之间基于成本的关系，而每个节点表示一个潜在的解决方案。在这种情况下，电阻器R2表示指定候选节点与其邻居之间的电阻，影响从该邻居接收的电流。相邻节点上目标函数的减小值导致等效电阻R2减小，从而根据欧姆定律增加流入候选节点的电流。如果下一个节点具有较差的目标值，则R2会增加，从而减少其对KCL更新的影响。这说明了优化中主要受性能优越的替代方案影响的内在倾向。因此，R2在确定搜索方向和收敛特性方面至关重要，在解间效应中充当可变权重。电路的配置，包括R2等组件，被选择来促进这种作为KLA框架基础的自适应和面向适应性的交互模型。

2.2 KLA的数学建模：基于KCL的公式化表达

在KLA算法中，节点电压间的电阻被建模为目标函数值的随机函数。节点间的能量损耗由电流平方乘以电阻决定，即$R_{ij}\times I_{ij}^2=\frac{1}{(rand+rand)}{\left(\frac{f(X_i)}{f(X_j)}\right)}^{2\times rand}\times I_{ij}^2$。该算法通过调整节点电压来最小化能量损耗并提高向最优解的收敛性。基于KCL推导的方程迭代更新节点电压，并引入系数模拟电流方向。KLA的简洁性和适应性使其适用于各类优化任务，且无需复杂控制参数。通过结合局部和全局搜索策略，还可进一步提升其处理复杂优化问题的能力。

算法中，任意两个节点$i$和$j$间的电阻$R_{ij}$建模为随机函数（如式(5)所示）。为适应优化过程，设定第$i$条支路（电流流入节点的支路）电阻为1欧姆，此时支路电压变化量等于电流变化量。节点KCL方程基于式(6)，通过优化节点电压（即种群位置）可降低$I_{ij}^2$值。如图2所示，节点电压和支路电流为标量参数，但算法建立了节点电压与种群成员的向量映射关系（变量$X$以向量形式表示）。为模拟电流方向对节点电压的影响，节点$i$和$j$间采用系数$\frac{f(X_j)-f(X_i)}{|f(X_j)-f(X_i)|+\epsilon }$（$\epsilon$为极小值）：若节点$i$电压（式(7)位置）小于节点$j$，则电流从$j$流向$i$（系数为正）；反之则电流反向（系数为负）；若两节点目标函数值相同则系数为零。对于规模为$Npop$的种群，新值$X_i^{k,\text{new}}$通过式(6)-(7)计算（$i=1,2,...,Npop$），其中$X_a$、$X_b$和$X_c$为随机选取的个体。
在每次迭代结束后，将这些Npop新成员的总体与前一个总体的Npop成员进行组合。对它们进行排序，以找到最佳的Npop总体，并将它们发送到下一次迭代。这个过程一直进行到最大选择的迭代次数结束，并为给定的问题选择最佳成员作为最终最优解。图2用于优化目的的等效电路在图3中进行了解释。让Xi是算法总体的第i个成员的位置向量（节点电压），让$f(X_i)$表示用于性能评估的相关目标函数值。

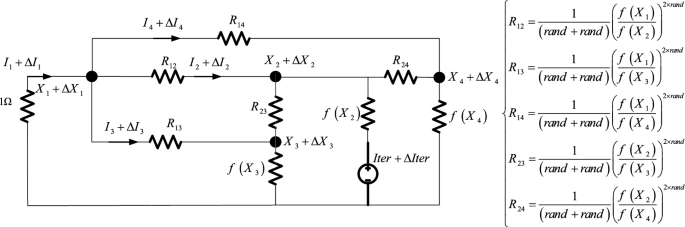
图3 用于算法目的的等效电路（示例2）
此外，图4提供了KLA的流程图和总体示意图。根据电路理论原理，建议的KLA框架有意地旨在最小化支路电流，尽管有恒定的电压供应。根据欧姆定律，电压和电流之间的关系是正比和反比的。当电压源保持恒定时，电阻的波动——由目标函数值动态表示——导致电流流动的变化。在这种情况下，最小化电流对应于确定降低电阻的途径（即更好的解决方案），从而减少功率损耗，如等式$P=I^{2}R$所示。这保证了优化过程自动追求能量损失最小的配置，代表了效率和精度方面的理想选择。因此，当前最小化在优化框架内作为与成本最小化相对应的代理目标。

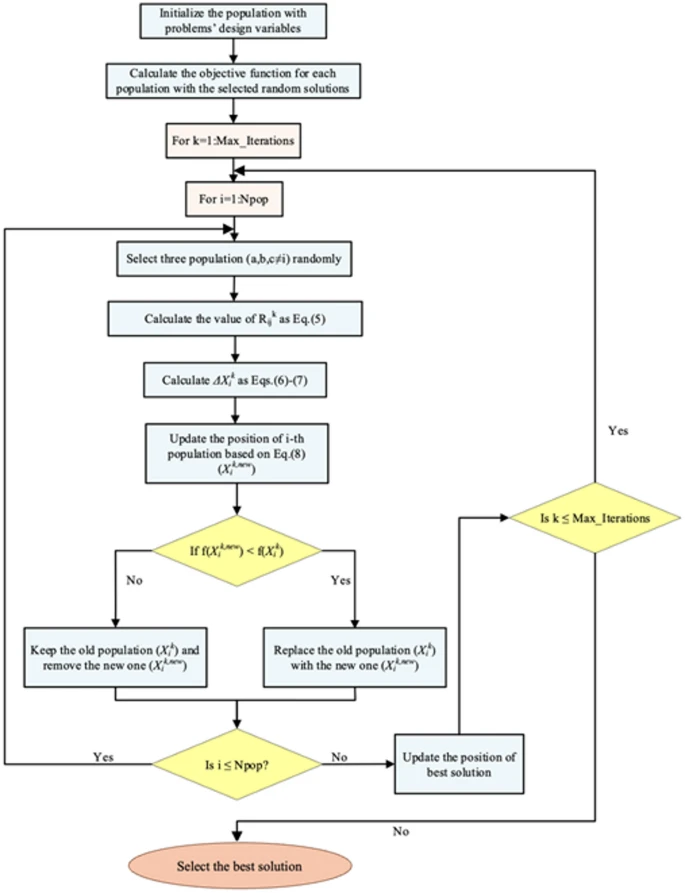
在KLA算法中，节点$i$和$j$间的电阻$R_{ij}^k$建模为随机函数（式(5)）：
$R_{ij}^k=\frac{1}{(rand+rand)}{\left(\frac{f\left(X_i^k\right)}{f\left(X_j^k\right)}\right)}^{2\times rand}$ (5)

节点电压更新量$\Delta X_i^k$通过KCL方程计算（式(6)）：
$\Delta X_i^k={\sum }_{j=a,b,c}\frac{\left(X_i^k-X_j^k\right)}{R_{ij}}$
$=(rand+rand)\times {\left(\frac{f\left(X_a^k\right)}{f\left(X_i^k\right)}\right)}^{2\times rand}\times \left(\frac{f\left(X_a^k\right)-f\left(X_i^k\right)}{|f\left(X_a^k\right)-f\left(X_i^k\right)|+\epsilon }\right)\left(X_i^k-X_a^k\right)$
$+(rand+rand)\times {\left(\frac{f\left(X_b^k\right)}{f\left(X_i^k\right)}\right)}^{2\times rand}\times \left(\frac{f\left(X_b^k\right)-f\left(X_i^k\right)}{|f\left(X_b^k\right)-f\left(X_i^k\right)|+\epsilon }\right)\left(X_i^k-X_b^k\right)$
$+(rand+rand)\times {\left(\frac{f\left(X_c^k\right)}{f\left(X_i^k\right)}\right)}^{2\times rand}\times \left(\frac{f\left(X_c^k\right)-f\left(X_i^k\right)}{|f\left(X_c^k\right)-f\left(X_i^k\right)|+\epsilon }\right)\left(X_i^k-X_c^k\right)$ (6)

电流方向系数定义为（式(7)）：
$\frac{f\left(X_j^k\right)-f\left(X_i^k\right)}{|f\left(X_j^k\right)-f\left(X_i^k\right)|+\epsilon }=\{\begin{array}{l}1\text{ if }f\left(X_i^k\right)<f\left(X_j^k\right),\\ -1\text{ if }f\left(X_i^k\right)>f\left(X_j^k\right),\\ 0\text{ if }f\left(X_i^k\right)=f\left(X_j^k\right),\end{array}$ (7)

节点位置更新公式为（式(8)）：
$X_i^{k,\text{new}}=X_i^k+\Delta X_i^k$ (8)

其中$rand$表示[0,1]区间均匀分布的随机数。该模型中，电阻$R_{ij}$由节点目标函数值显式决定，确保性能更优的节点（成本更低）具有更小电阻，根据欧姆定律吸引更大电流。电流方向和大小通过式(7)中的极小系数$\epsilon$调控，保证更新过程促使电流从高电阻节点向低电阻节点迁移。式(6)直接体现KCL定律，保证节点所有流入流出电流的代数和为零，确保KLA更新过程中各种群成员影响的平衡。

图5以伪代码形式展示了KLA的迭代流程，每轮迭代包含：基于KCL的电流变异、目标函数评估和种群更新选择。该高效框架凸显算法无需参数的特性，能低复杂度处理各类优化问题。
KLA将元启发式原理与电路类比优雅地交织在一起，编排出进化适应和优化的交响乐。在算法对成本最小化和效率最大化的坚定追求的指导下，每次迭代都进行了变异、选择和评估的和谐舞蹈。通过这种计算和电气领域的无缝融合，KLA以一种*****的独创性出现，照亮了通往全局优化目标的道路。测试函数和基准的选择对于确定优化算法的性能很重要。在本研究中，KLA的性能使用了17个基准函数的广泛选择进行了测试，这些函数包括单峰、多模态和复合函数。选择这些函数来模拟现实生活中的优化问题；它们的全局最优数量各不相同，包括简单的景观和多个局部最优。例如，单峰函数用于评估算法收敛到全局最小值的能力，而多模态和复合函数用于评估算法避免陷入局部最优值和保持种群多样性的能力。

function [Best_fitness, Xbest, Cost_Rsult] = KLA(nPop, MaxIt, lb, ub, nVar, fobj)
    VarSize = [1 nVar];        %%% Decision Variables Matrix Size
    VarMin = lb;             %%% Decision Variables Lower Bound
    VarMax = ub;             %%% Decision Variables Upper Bound
    ebs = realmin;
    solutions.Position=[];
    solutions.Cost=[];
    %%% Initialize Population Array
    pop=repmat(solutions,nPop,1);
    %%% Initialize Best Solution Ever Found
    BestSol.Cost=inf;
    TT=-inf;
    %%% Create Initial Population
    for i=1:nPop
        pop(i).Position=unifrnd(VarMin,VarMax,VarSize);
        pop(i).Cost = fobj(pop(i).Position);
        %%% pop(i).Cost=feval(fhd,pop(i).Position',func_num);%if you want to use form  Cost Functions CEC 2014
        if pop(i).Cost<=BestSol.Cost
            BestSol=pop(i);
        end
        if pop(i).Cost>TT
            TT=pop(i).Cost;
        end
        BestCost1(i)=BestSol.Cost;
    end
    %%% Array to Hold Best Cost Values
    BestCost=zeros(MaxIt,1);
    %%% KLA Main Loop
    it=nPop;
    %%% for it=1:Iter %%% If you want to use it in terms of repetition.
    while it<=MaxIt
        newpop=repmat(solutions,nPop,1);
        for i=1:nPop
            newpop(i).Cost = inf;
            A=randperm(nPop);
            A(A==i)=[];  
            a=A(1);
            b=A(2);
            jj=A(3);
                        
            q=((pop(i).Cost-pop(jj).Cost)+ebs)/(abs((pop(i).Cost-pop(jj).Cost))+ebs);
            Q=(pop(i).Cost-pop(a).Cost)/(abs((pop(i).Cost-pop(a).Cost))+ebs);
            Q2=(pop(i).Cost-pop(b).Cost)/(abs((pop(i).Cost-pop(b).Cost))+ebs);
            q1=((pop(jj).Cost)/(pop(i).Cost))^(2*rand);
            Q1=((pop(a).Cost)/(pop(i).Cost))^(2*rand);
            Q21=((pop(b).Cost)/(pop(i).Cost))^(2*rand);
            S1=q1*q*rand(VarSize).*(pop(jj).Position-pop(i).Position);
            S2=Q*Q1*rand(VarSize).*(pop(a).Position-pop(i).Position);
            S3=Q2*Q21*rand(VarSize).*(pop(b).Position-pop(i).Position);
            S=(rand+rand)*S1+(rand+rand)*S2+(rand+rand)*S3;
            newsol.Position =pop(i).Position+S;
            newsol.Position=max(newsol.Position,VarMin);
            newsol.Position=min(newsol.Position,VarMax);
            
            newsol.Cost = fobj(newsol.Position);
            %%% newsol.Cost=feval(fhd,newsol.Position',func_num); %%%if you want to use form  Cost Functions CEC 2014 or other CEC
            if newsol.Cost<=pop(i).Cost
                pop(i) = newsol;
                if pop(i).Cost<=BestSol.Cost
                    BestSol=pop(i);
                end
            end
            it=it+1;
            BestCost1(it)=BestSol.Cost;  
        end
        BestCost(it)=BestSol.Cost;
    end
    Best_fitness = BestSol.Cost;
    Xbest = BestSol.Position;
    Cost_Rsult = BestCost1;
end

Ghasemi, M., Khodadadi, N., Trojovský, P. et al. Kirchhoff’s law algorithm (KLA): a novel physics-inspired non-parametric metaheuristic algorithm for optimization problems. Artif Intell Rev 58, 325 (2025). https://doi.org/10.1007/s10462-025-11289-5