目录
以升序为例
1.计数排序的思想
前面我们学习的快排、归并排序、希尔排序........等等都是需要比较大小才能使数组有序的方法,而计数排序属于非比较排序
计数排序的核心思想在于,借助计数数组来统计原数组中各个元素的出现次数,随后通过覆盖写等一系列操作,最终达成将原数组排序为有序序列的目的
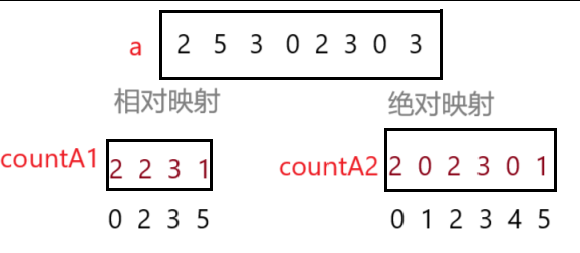
2.计数排序图解
3.计数排序代码逻辑
3.1求原数组最大最小值及计数数组的创建
//求最大最小值
int max = a[0], min = a[0];
for (int i = 1; i < n; ++i){
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
//开计数数组
int range = max - min + 1;
int* countA = (int*)calloc(range, sizeof(int));
if (!countA){
perror("malloc fail");
return;
}这是一种相对位置映射的思想,简单来说
原数组的最小元素代表计数数组的第一个位置,以此类推,最大值代表计数数组的最后一个位置
相对映射比绝对映射节省空间
绝对映射需要开至少(万一有负数)最大值个元素空间,当最大值是一万,但最小值是9999时,空间浪费极大,所以实践中多使用相对位置映射
所以计数数组 countA 的大小通常为 max - min + 1 ,元素初始值均为0
3.2计数
for (int i = 0; i < n; ++i){
countA[a[i] - min]++;
}min 代表的是计数数组的第一个位置,a[i] - min 计算的就是 a[i] 与 min 之间的差值,
这个差值正好对应 a[i] 代表的计数数组位置
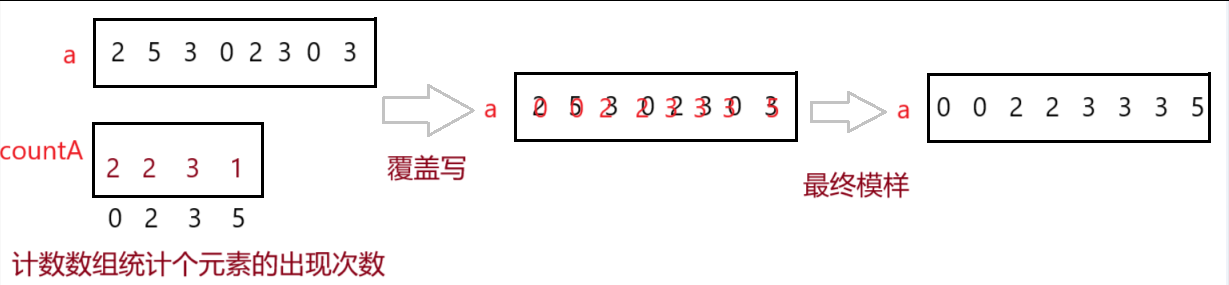
3.3覆盖写
遍历计数数组,根据原数组各元素的出现次数进行覆盖写
int j = 0;
for (int i = 0; i < range; ++i){
while (countA[i]--){
a[j++] = i + min;
}
}for循环是遍历计数数组,while循环的循环次数是原数组各元素的出现次数
计数数组的下标 i 是 原数组各元素与min 的差值,即 i = a[ j ] - min
3.4释放资源
free(countA);
countA = NULL;防止内存泄漏哦~
4.计数排序的注意事项
计数排序只能排序整型
根据上述思想,计数排序更适合 范围集中 的 整型数组
5.计数排序的时间复杂度与空间复杂度
计数排序的时间复杂度 基于 原数组和计数数组的 遍历操作,
所以时间复杂度为 O(N + range),当range接近N是,计数排序的效率极高!
计数排序的空间复杂度基于计数数组的创建
所以空间复杂度为O(range)
当然,如果有输出数组的创建,空间复杂度为 O(N + range)