接下来,我们就进入二叉树的部分。
首先,笔者介绍一下树的概念:树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。树有一个特殊的节点,称作根节点,这个根节点并无前驱节点,这个根节点之外,其余节点别分为互不相交的集合,其中每一个结合Ti又是一颗子树,树是递归定义的。如果是一个树形结构的子树有交集,那么就不能称之为树形结构。
1.结点的度:一个结点含有的子树的个数
2.叶结点(终端结点):度为0
3. 非终端点(分支结点):度不为0
4.双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点
5.孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点
6.兄弟结点:具有相同父结点的结点互称为兄弟结点
7.树的度:一棵树中,最大的结点的度称为树的度
8.结点的层次:从根开始定义起,根为第1层,根的子结点为第二层
9.树的高度或深度:树中结点的最大层次;
10.堂兄弟结点:双亲在同一层的结点互为堂兄弟
11.结点的祖先:从根到该结点所经分支上的所有结点
12.子孙:以某结点为根的子树中任一结点都称为该结点的子孙
13.森林:由m(m>0)棵互不相交的树组成的集合
基于此,我们可以看到,树的表示很麻烦,事实上,种类也很多,在这里我们介绍一种最常用的表示法——孩子兄弟表示法:
typedef int DataType;
struct Node
{
struct Node* firstChild1; // 第一个孩子结点
struct Node* pNextBrother; // 指向其下一个兄弟结点
DataType data; // 结点中的数据域
}就像上面写的,笔者直接定义了两个指针,一个指向孩子,一个指向相邻的下一个兄弟:
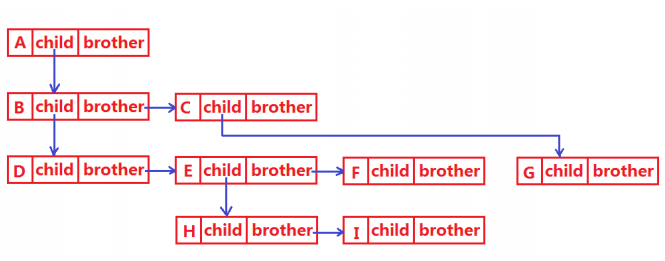
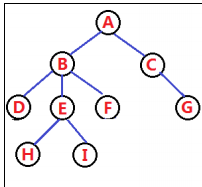
下面,我们具体介绍一种特殊的树——二叉树,进而引出一种数据结构——堆。
二叉树是结点的一个有限集合,这个集合要么为空,要么是由一个根结点加上两棵别称为左子树和右子树的二叉树组成:
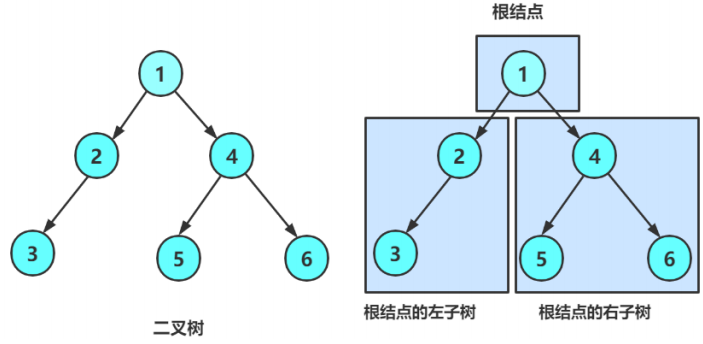
从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
其实所有的二叉树都是以下几种情况复合而成:
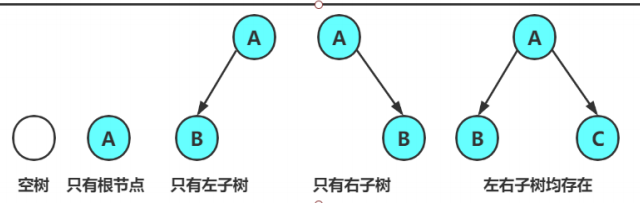
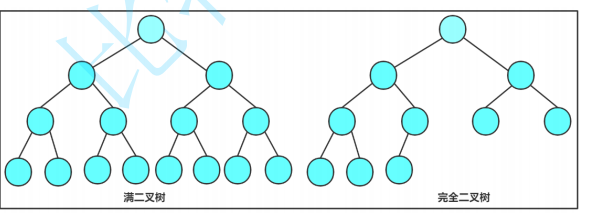
然后我们在介绍两个特殊的二叉树——满二叉树,完全二叉树
满二叉树:每一层的结点数都到达最大值,这个二叉树就是满二叉树,且结点总数为2^k-1。
完全二叉树:完全二叉树是一种效率很高的数据结构 ,对于深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树种编号为1至n的结点一一对应是称为完全二叉树,除最后一层外,每一层的节点都满了,最后一层的节点都集中在最左边。
二叉树也有若干性质:
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1)个结点.
2. 若规定根结点的层数为1,则深度为h的二叉树的最大结点数是2^h-1
3.对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有n0=n2+1


二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。顺序结构就是用数组存储,链式结构就是用链表存储。
下面我们先学习顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结
构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统
虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
如果给定一个集合,其中元素按照完全二叉树的形式存储在一个一维数组中,而且满足大小关系不变,则称为大堆(小堆),也就是说堆中某个结点的值不大于或不小于其父亲的值,堆总是一颗完全二叉树。
下面我们着重来实现堆:
首先,我们给出接口的声明:
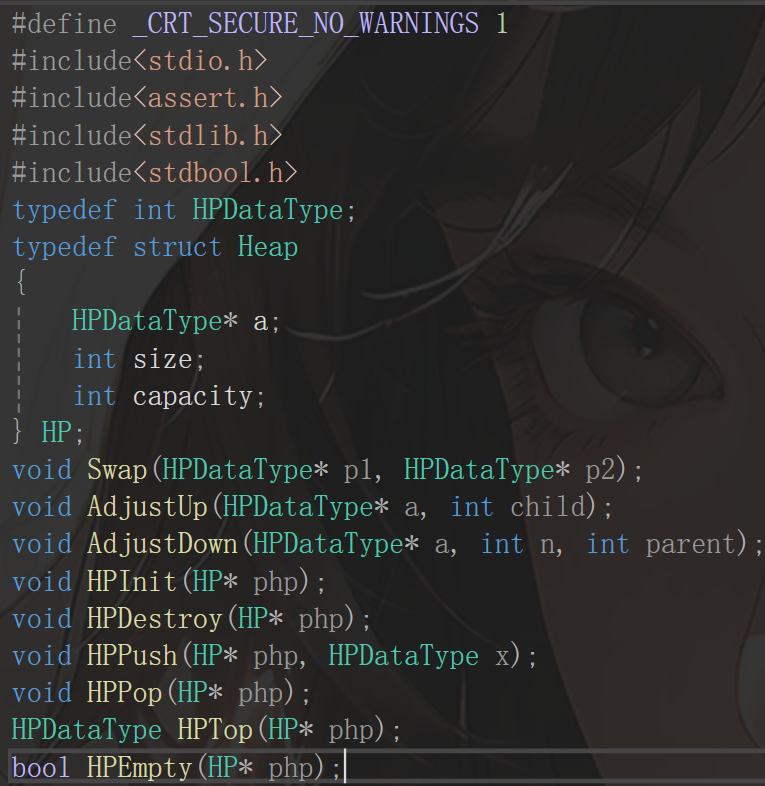
如上图所示,因为堆在物理结构上是动态数组,所以定义的时候就应该按照动态数组结构体的方式进行定义:先定义一个指针,然后定义动态数组的长度,最后定义容量。然后就是声明了几个接口:交换两个数组内容位置,向上调整算法,向下调整算法,这三个相当于后面需要用的组件。再往下就是很平常的各种接口:定义,销毁,插入,删除,取顶部,判空。
下面就来一个一个实现:
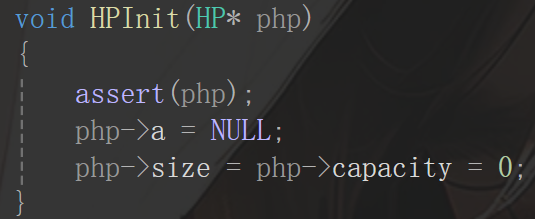
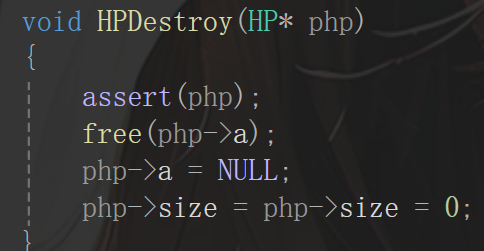
这两个接口是老生常谈的问题了,比较简单,笔者略去。
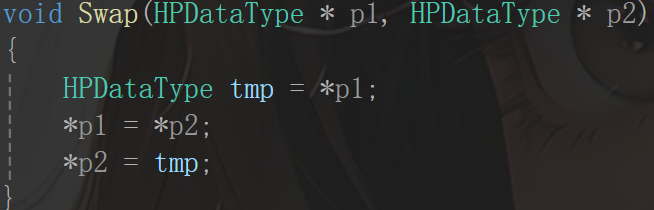
这个接口是实现数组两个元素的值交换了,也比较简单。

这就是向上调整算法,所谓的向上调整算法,就是根据孩子的下标,求出父亲的下标,这个父子下标的关系很容易推出,然后进入一个循环,不断调整关系,如果孩子<父亲,而且现在在建小堆,那么就应该把孩子和父亲交换,也就是swap函数,值交换之后,再交换两者对应的下标(索引),进而完成了向上调整,如果child为0,那么他就到了根节点,自然break了。
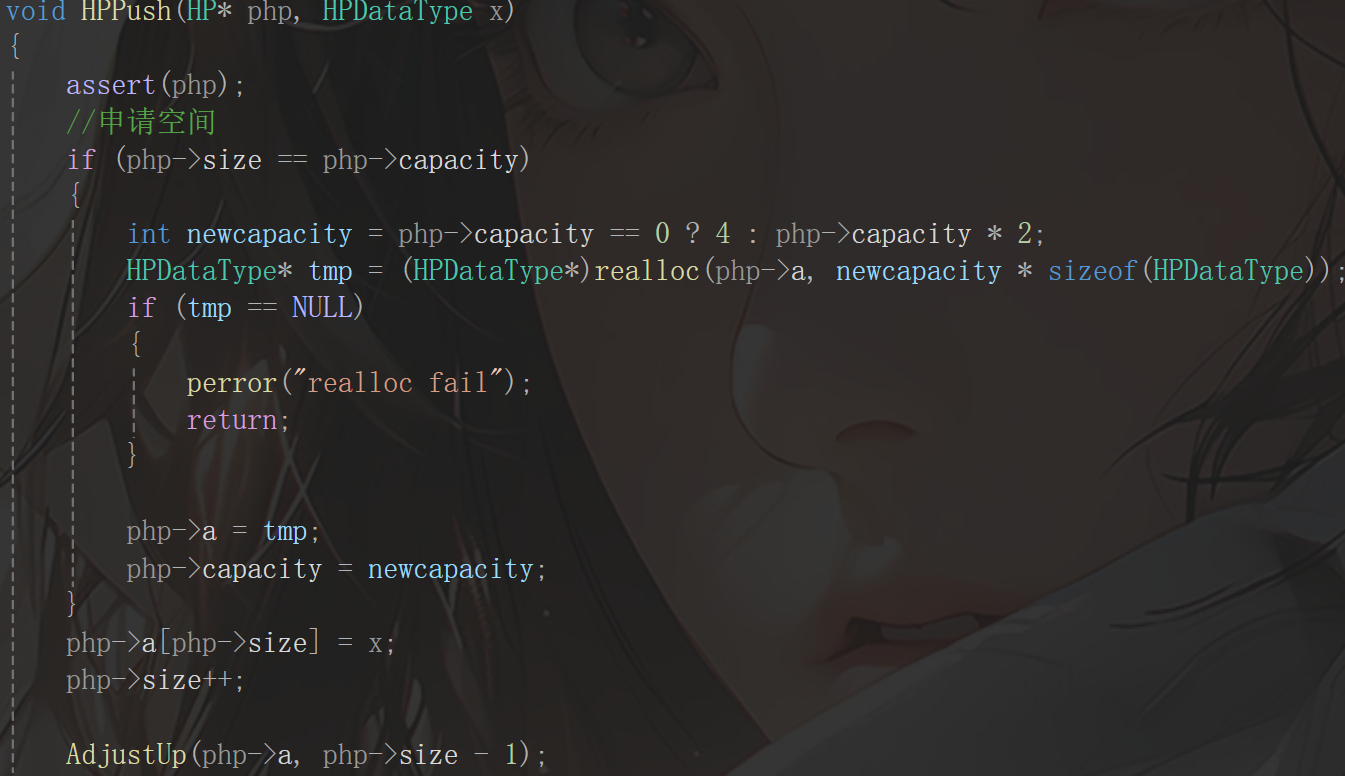
这个接口是用来实现堆的插入的,需要用到向上调整算法,故在其下面完成,这个接口实现其实并不难,很多都是老生常谈的问题,比如申请空间,断言,后面的就是真正意义上的堆的插入,首先先在最后一个位置插入x,然后将size++,最后一定要用向上调整算法,因为插入的东西不知道是否是孩子,如果不是,那就破坏了堆的结构,至于向上调整算法的参数一定要注意用size-1,因为此时size已经增加了,所以最后一个元素的下标仍然是size-1。
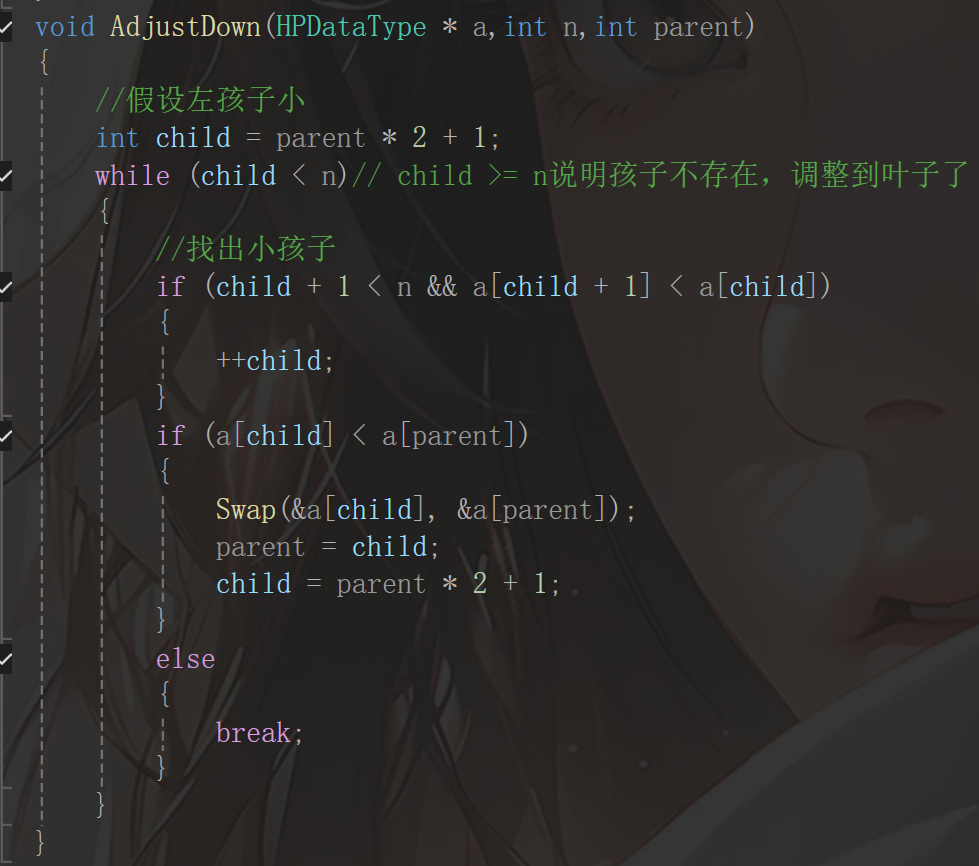
这是向下调整算法,其中n是有效元素的个数,parent是父节点对应的下标,需要注意的是,向下调整算法必须保证不能超出有效元素的个数,所以while中的条件就出来了,然后就是进行循环体的书写,因为在一层里,其实是无序的,所以不确定左孩子和右孩子谁大,所以应该用假设法,然后就得先找出小的那个孩子,然后就是进行交换,这部分就比较简单了。
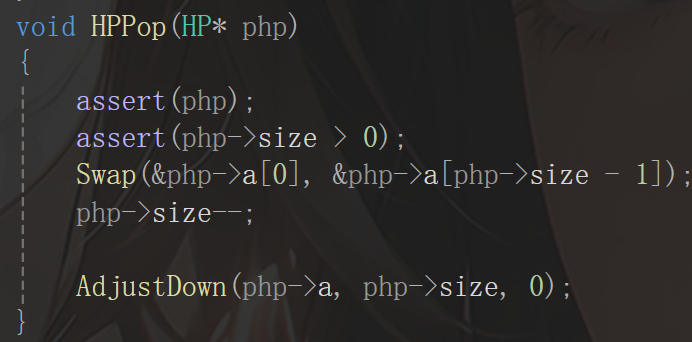
然后就是删除的操作,删除之前先交换一下,也就是把根节点和最后一个结点交换,这样可以很好的避免破坏堆的结构,因为一旦不交换,直接删除,那么就会导致亲缘关系改变。最后传参的时候一定转0,因为此时父节点是整个数组的第一个元素。
最后这两个比较简单,笔者不在多说。