目录
二、简单选择排序(simple selection sort)
一、插入排序
常见的排序算法有:
而本篇文章要介绍的是选择排序。
插入排序可以分为 选择排序(simple selection sort) 和 堆排序(heap sort) 。
二、简单选择排序(simple selection sort)
1. 基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
如果选的是最大的一个元素,则为排升序。
如果选的是最小的一个元素,则为排降序。
2. 思路介绍
思路:
- 将整个数据划分为有序区和无序区,初始时有序区为空,无序区含有待排序的所有数据。
- 在无序区中选取最小的数据,将其与无序区中的第一个数据交换,使得有序区增加一个数据,同时无序区减少一个数据。
- 不断重复步骤2,直到无序区只剩一个数据。
对于一组数据:3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 它的排序个过程如下:
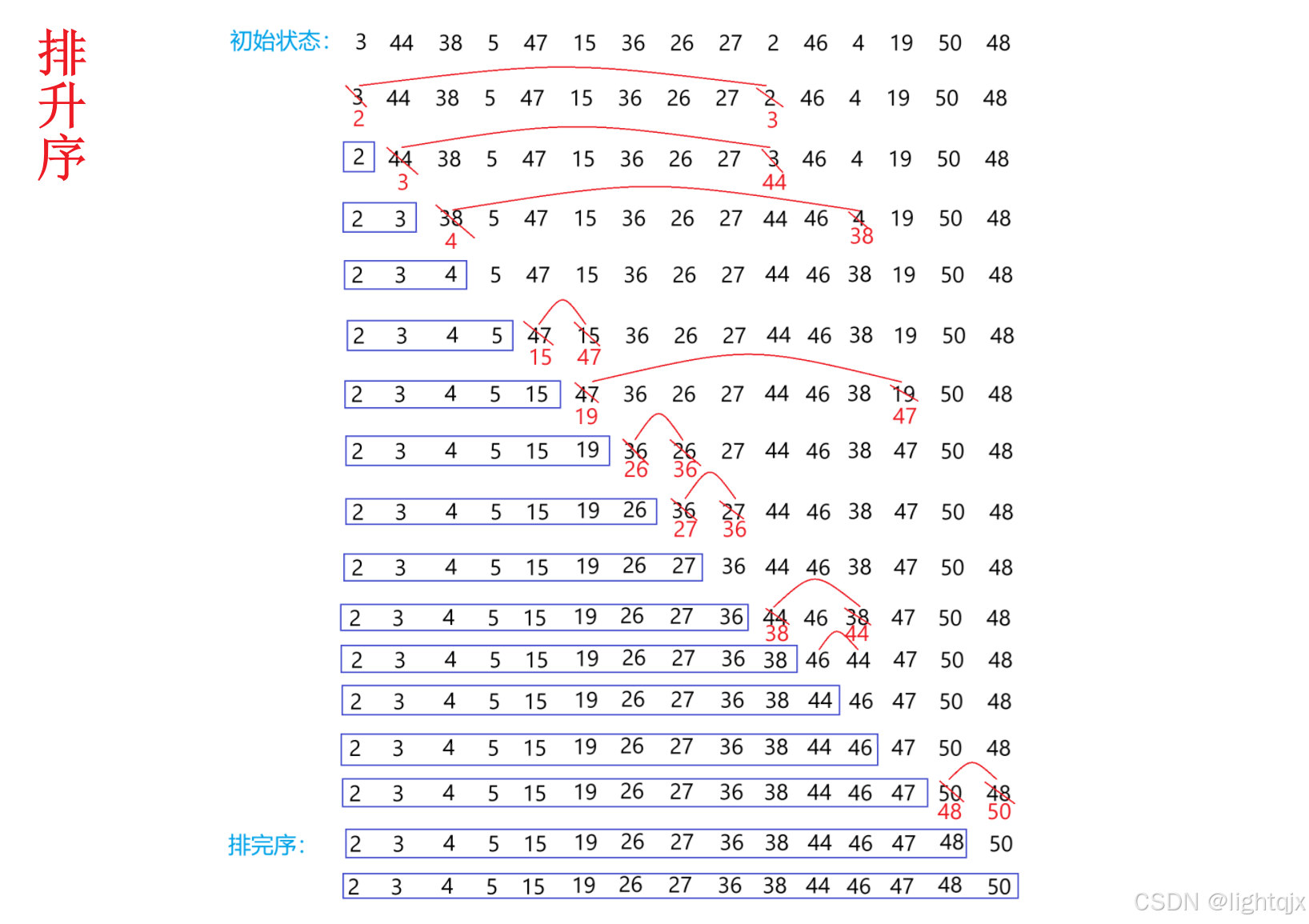
排序动图如下:
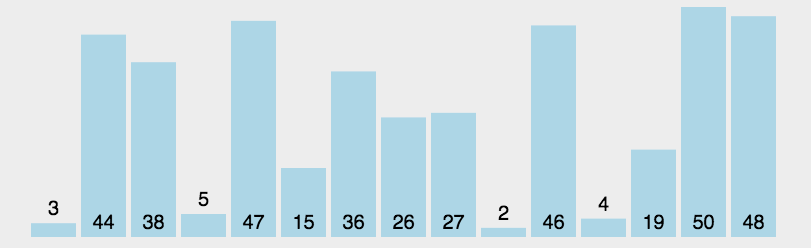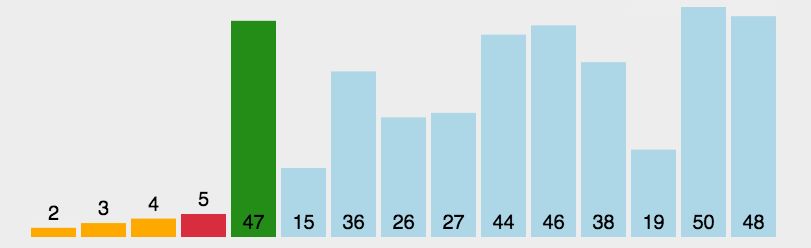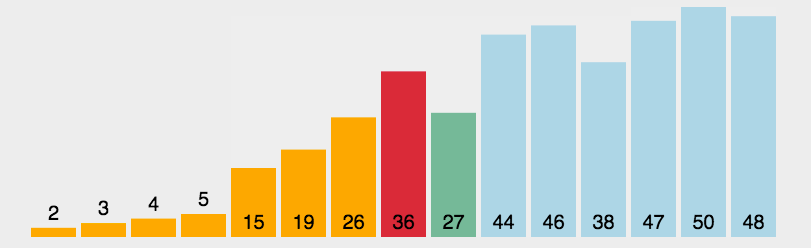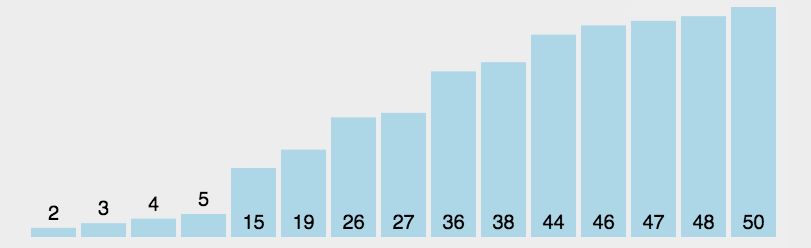
3. 代码实现
C语言代码实现:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
// 选择排序
void SelectSort(int* a, int n)
{
int left = 0;// 无序区第一个的下标
while(left < n - 1)
{
int mini = left + 1;// 无序区最小值的下标
// 遍历除第一个无序区元素的其他元素
for (int i = left + 1; i < n; i++)
{
// 寻找最小值下标
if (a[i] < a[mini])
{
mini = i;
}
}
if (mini != left)
{
Swap(&a[left], &a[mini]);
}
left++;
}
}可以发现上面的选择排序是一个一个的寻找,再排序。这样效率会很低。
所以,可以改进一下:
从左右两边同时开始选择,排升序的话,可以在左边选择最小值进行交换,在右边选择最大值进行交换。则C语言代码实现;
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort(int* a, int n)
{
int left = 0;//左边无序区第一个
int right = n - 1;//右边无序区第一个
while (left < right)
{
int mini = left;
int maxi = right;
for (int i = left; i <= right; i++)
{
//选最小值下标
if (a[mini] > a[i])
{
mini = i;
}
//选择最大值下标
if (a[maxi] < a[i])
{
maxi = i;
}
}
Swap(&a[left], &a[mini]);
// 如果left和maxi重叠,交换后修正一下
if (left == maxi)
{
maxi = mini;
}
Swap(&a[right], &a[maxi]);
++left;
--right;
}
}4. 特性总结
简单选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。所以实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
三、堆排序(heap sort)
1. 基本思想
堆排序 是指利用堆(一种完全二叉树)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据 。
需要注意的是:
排升序 要 建大堆,排降序要建小堆。
然后利用堆的删除思想,进行排序。
2. 思路介绍
思路:
- 建堆:从倒数的第一个非叶子节点的子树开始向下调整调整,一直调整到根节点的树,就可以调整成想要的堆。
- 堆的删除:将堆顶的元素与最后一个元素进行交换,在对此时的堆顶元素进行向下调整。
- 重复次步骤2操作,直到堆中只有一个元素。
以建大堆排升序例:
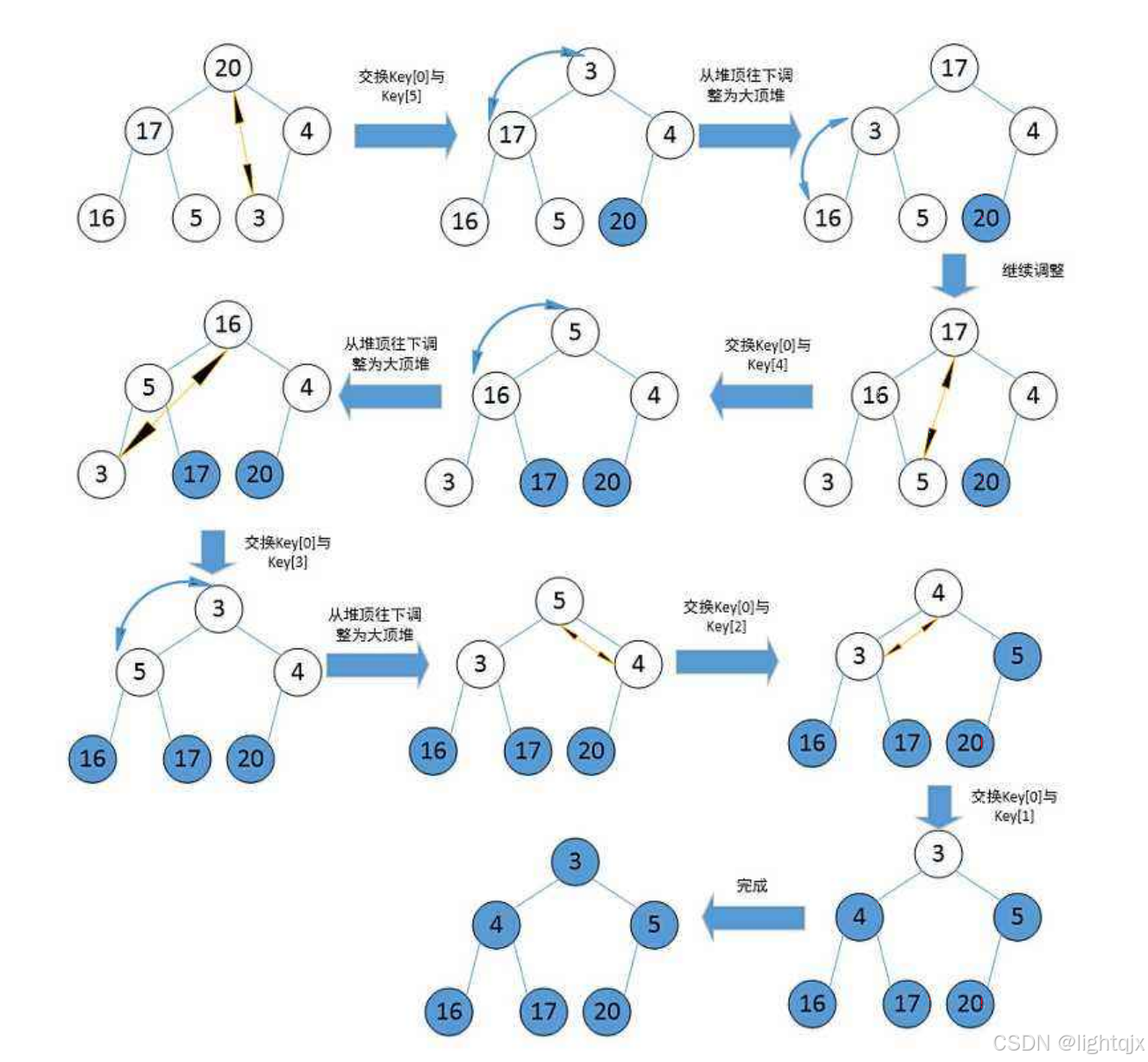
3. 代码实现
C语言代码实现:
// 堆排序
//向下调整-建大堆
void AdjustDwon(int* a, int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
//选择两个孩子中较大的一个
if (child + 1 < n && a[child] < a[child + 1])
{
child++;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void HeapSort(int* a, int n)
{
//建大堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDwon(a, n, i);
}
//堆的删除
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDwon(a, end, 0);
end--;
}
}4. 特性总结
堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
四、总结
- 简单选择排序通过每次选择最小(或最大)元素进行交换,逐步构建有序序列,其时间复杂度为O(N^2)。
- 堆排序则利用堆的数据结构,通过建堆和堆删除操作实现排序,效率更高。
- 时间复杂度为O(N*logN)。两种算法都具有空间复杂度O(1)的特点,但都不稳定。
感谢各位观看!希望能多多支持!