相机坐标系与世界坐标系的点相互转换:原理、可视化与实践
一、背景:为什么需要坐标系转换?
在自动驾驶、计算机视觉和机器人领域,我们经常需要处理多个坐标系中的数据。每个传感器(如相机、激光雷达)都有自己独立的坐标系,而为了理解物体在真实世界中的位置,我们需要将这些局部坐标系的数据转换到一个统一的全局坐标系(世界坐标系)中。
具体到我的项目需求:
- 我需要验证BEV(鸟瞰图)感知模块中6个相机的外参矩阵是否正确
- 通过可视化绘制每个相机及其父坐标系的位置和朝向
- 判断相机安装位置和朝向是否符合实际物理布局
坐标系转换是理解传感器数据融合的基础,也是实现精准感知的关键环节。本文将详细解释坐标系转换的原理、方法,并通过实际可视化案例展示如何验证外参的正确性。
二、理论基础:坐标系转换的核心原理
1. 外参的定义与作用
相机外参(Extrinsic Parameters)由旋转矩阵R和平移向量t组成,描述了两个坐标系之间的刚体变换关系:
- 旋转矩阵R:3×3正交矩阵(满足 R T = R − 1 R^T = R^{-1} RT=R−1),表示坐标系间的旋转变换
- 平移向量t:3维列向量,表示坐标系原点间的位移
数学表示:
- P c P_c Pc:点在相机坐标系中的坐标(齐次坐标 [ X c , Y c , Z c , 1 ] T [X_c, Y_c, Z_c, 1]^T [Xc,Yc,Zc,1]T)
- P w P_w Pw:点在世界坐标系中的坐标(齐次坐标 [ X w , Y w , Z w , 1 ] T [X_w, Y_w, Z_w, 1]^T [Xw,Yw,Zw,1]T)
2. 相机→世界的变换(C2W)
当外参定义为从相机坐标系到世界坐标系的变换:
相机点转世界点:
P w = R C2W ⋅ P c + t C2W P_w = R_{\text{C2W}} \cdot P_c + t_{\text{C2W}} Pw=RC2W⋅Pc+tC2W其中:
- R C2W R_{\text{C2W}} RC2W:相机坐标系到世界坐标系的旋转矩阵
- t C2W t_{\text{C2W}} tC2W:相机坐标系原点在世界坐标系中的位置
世界点转相机点(逆变换):
P c = R C2W T ⋅ ( P w − t C2W ) P_c = R_{\text{C2W}}^T \cdot (P_w - t_{\text{C2W}}) Pc=RC2WT⋅(Pw−tC2W)
3. 世界→相机的变换(W2C)
当外参定义为从世界坐标系到相机坐标系的变换:
世界点转相机点:
P c = R W2C ⋅ P w + t W2C P_c = R_{\text{W2C}} \cdot P_w + t_{\text{W2C}} Pc=RW2C⋅Pw+tW2C其中:
- R W2C R_{\text{W2C}} RW2C:世界坐标系到相机坐标系的旋转矩阵
- t W2C = − R W2C T ⋅ t C2W t_{\text{W2C}} = -R_{\text{W2C}}^T \cdot t_{\text{C2W}} tW2C=−RW2CT⋅tC2W(与C2W中的平移向量相关)
相机点转世界点(逆变换):
P w = R W2C T ⋅ ( P c − t W2C ) P_w = R_{\text{W2C}}^T \cdot (P_c - t_{\text{W2C}}) Pw=RW2CT⋅(Pc−tW2C)
4. 四元数到旋转矩阵的转换
在实际应用中,旋转常以四元数形式存储(更紧凑,无万向锁问题)。四元数 q = [ w , x , y , z ] q = [w, x, y, z] q=[w,x,y,z](标量w在前)转换为旋转矩阵的公式:
R = [ 1 − 2 y 2 − 2 z 2 2 x y − 2 w z 2 x z + 2 w y 2 x y + 2 w z 1 − 2 x 2 − 2 z 2 2 y z − 2 w x 2 x z − 2 w y 2 y z + 2 w x 1 − 2 x 2 − 2 y 2 ] R = \begin{bmatrix} 1-2y^2-2z^2 & 2xy-2wz & 2xz+2wy \\ 2xy+2wz & 1-2x^2-2z^2 & 2yz-2wx \\ 2xz-2wy & 2yz+2wx & 1-2x^2-2y^2 \end{bmatrix} R= 1−2y2−2z22xy+2wz2xz−2wy2xy−2wz1−2x2−2z22yz+2wx2xz+2wy2yz−2wx1−2x2−2y2
5. 核心要点总结
C2W外参:
P w = R ⋅ P c + t P_w = R \cdot P_c + t Pw=R⋅Pc+t
P c = R T ⋅ ( P w − t ) P_c = R^T \cdot (P_w - t) Pc=RT⋅(Pw−t)W2C外参:
P c = R ⋅ P w + t P_c = R \cdot P_w + t Pc=R⋅Pw+t
P w = R T ⋅ ( P c − t ) P_w = R^T \cdot (P_c - t) Pw=RT⋅(Pc−t)
旋转矩阵 R R R由四元数转换而来,且满足正交矩阵性质 R T = R − 1 R^T = R^{-1} RT=R−1。
三、自动驾驶中的坐标系
不同系统使用不同的坐标系标准,理解这些差异至关重要:
1. Apollo中的坐标系定义
| 坐标系类型 | X轴方向 | Y轴方向 | Z轴方向 | 典型应用 |
|---|---|---|---|---|
| 相机坐标系 | 向右 | 向下 | 向前(光轴方向) | 图像处理 |
| 激光雷达坐标系 | 向前 | 向左 | 向上 | 点云处理 |
| 车辆坐标系 | 向右 | 向前 | 向上 | 车辆控制 |
2. 坐标系可视化
Apollo相机坐标系
Apollo激光雷达坐标系:
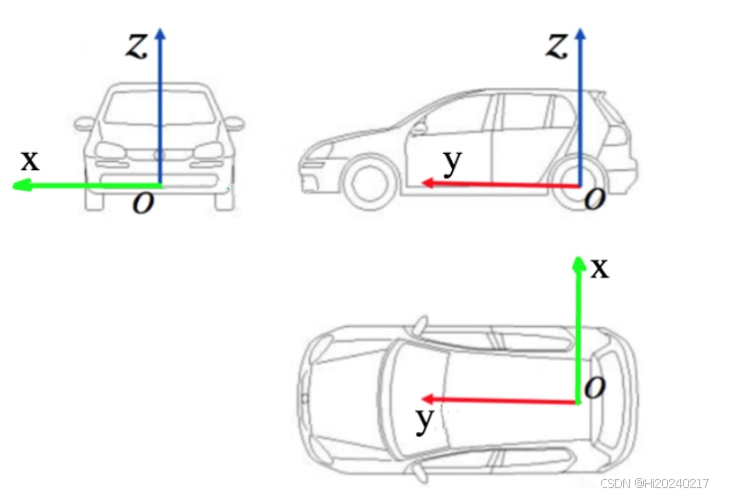
Apollo车辆坐标系:
四、外参可视化实践
1. NuScenes数据集外参可视化
import numpy as np
import matplotlib.pyplot as plt
from pyquaternion import Quaternion
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.lines import Line2D # 导入Line2D用于创建自定义图例
# 相机坐标系到LiDar坐标系的变换 (相机名称, 四元数(w,x,y,z), 位置(x,y,z))
camera_data = [
["CAM_FRONT ",[4.9980e-01,-5.0303e-01,4.9978e-01,-4.9737e-01],[ 1.7008,1.5946e-02,1.5110e+00]],
["CAM_FRONT_RIGHT ",[2.0603e-01,-2.0269e-01,6.8245e-01,-6.7136e-01],[ 1.5508,-4.9340e-01,1.4957e+00]],
["CAM_BACK_RIGHT ",[1.2281e-01,-1.3240e-01,-7.0043e-01,6.9050e-01],[ 1.0149,-4.8057e-01,1.5624e+00]],
["CAM_BACK ",[5.0379e-01,-4.9740e-01,-4.9419e-01,5.0455e-01],[ 0.0283,3.4514e-03,1.5791e+00]],
["CAM_BACK_LEFT ",[6.9242e-01,-7.0316e-01,-1.1648e-01,1.1203e-01],[ 1.0357,4.8480e-01,1.5910e+00]],
["CAM_FRONT_LEFT ",[6.7573e-01,-6.7363e-01,2.1214e-01,-2.1123e-01],[ 1.5239,4.9463e-01,1.5093e+00]]
]
arrow_length = 0.2
arrow_length_ratio=0.3
# 创建3D图形
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
# 车辆体坐标系原点
ax.scatter(0, 0, 0, c='r', s=100, label='Lidar Origin')
ax.quiver(0,0,0,0.5,0,0,color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0.5,0,color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0,0.5,color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
# 设置坐标轴范围
ax.set_xlim([-4, 4])
ax.set_ylim([-4, 4])
ax.set_zlim([-4, 4])
# 设置坐标轴标签
ax.set_xlabel('X (Forward)')
ax.set_ylabel('Y (Left)')
ax.set_zlabel('Z (Up)')
ax.set_title("Inferring the camera's position and orientation via nuscenes v1.0-mini extrinsics")
# 处理每个相机数据
for name, quat_vals, pos_vals in camera_data:
# 创建四元数 (w, x, y, z)
w,x,y,z=quat_vals
q = Quaternion((w,x,y,z))
R = q.rotation_matrix # 世界坐标系到相机坐标系的旋转
matrix = np.eye(4)
matrix[:3, :3] = R
matrix[:3, 3] = np.array(pos_vals)
R = matrix[:3, :3] # 旋转矩阵
position = matrix[:3, 3] # 平移向量
# 绘制相机位置
ax.scatter(position[0], position[1], position[2], s=32, label=name)
arrow_length = 0.3
# 绘制相机坐标的Z轴(从原点向Z轴方向长1个单位的线)
# 1.将Z轴一个单位向量转换到世界坐标系
z_axis_unit_vector = np.array([0, 0, 1])
z_axis_unit_vector_w = R@z_axis_unit_vector
z_axis_unit_vector_w =z_axis_unit_vector_w* arrow_length
# 2.绘制朝向箭头
ax.quiver(
position[0], position[1], position[2],
z_axis_unit_vector_w[0],
z_axis_unit_vector_w[1],
z_axis_unit_vector_w[2],
color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+z_axis_unit_vector_w), "Z", fontsize=5)
# 绘制相机坐标的Y轴(从原点向Y轴方向长1个单位的线)
# 1.将Y轴一个单位向量转换到世界坐标系
y_axis_unit_vector = np.array([0, 1, 0])
y_axis_unit_vector_w = R@y_axis_unit_vector
y_axis_unit_vector_w = y_axis_unit_vector_w*arrow_length
# 2.绘制朝向箭
ax.quiver(
position[0], position[1], position[2],
y_axis_unit_vector_w[0],
y_axis_unit_vector_w[1],
y_axis_unit_vector_w[2],
color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+y_axis_unit_vector_w), "Y", fontsize=5)
# 绘制相机坐标的X轴(从原点向Y轴方向长1个单位的线)
# 1.将X轴一个单位向量转换到世界坐标系
x_axis_unit_vector = np.array([1, 0, 0])
x_axis_unit_vector_w = R@x_axis_unit_vector
x_axis_unit_vector_w = x_axis_unit_vector_w*arrow_length
# 2.绘制朝向箭头
ax.quiver(
position[0], position[1], position[2],
x_axis_unit_vector_w[0],
x_axis_unit_vector_w[1],
x_axis_unit_vector_w[2],
color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+x_axis_unit_vector_w), "X", fontsize=5)
# 添加相机名称标签
ax.text(position[0], position[1], position[2] + 0.1, name, fontsize=5)
# 添加坐标轴颜色图例
axis_legend_elements = [
Line2D([0], [0], color='red', lw=2, label='X Axis'),
Line2D([0], [0], color='lime', lw=2, label='Y Axis'),
Line2D([0], [0], color='blue', lw=2, label='Z Axis')
]
# 合并两个图例:相机位置图例 + 坐标轴颜色图例
handles, labels = ax.get_legend_handles_labels()
all_handles = handles + axis_legend_elements
# 添加合并后的图例
ax.legend(handles=all_handles, loc='upper left')
# 设置视角
ax.view_init(elev=25, azim=-60)
# 显示图形
plt.tight_layout()
plt.show()
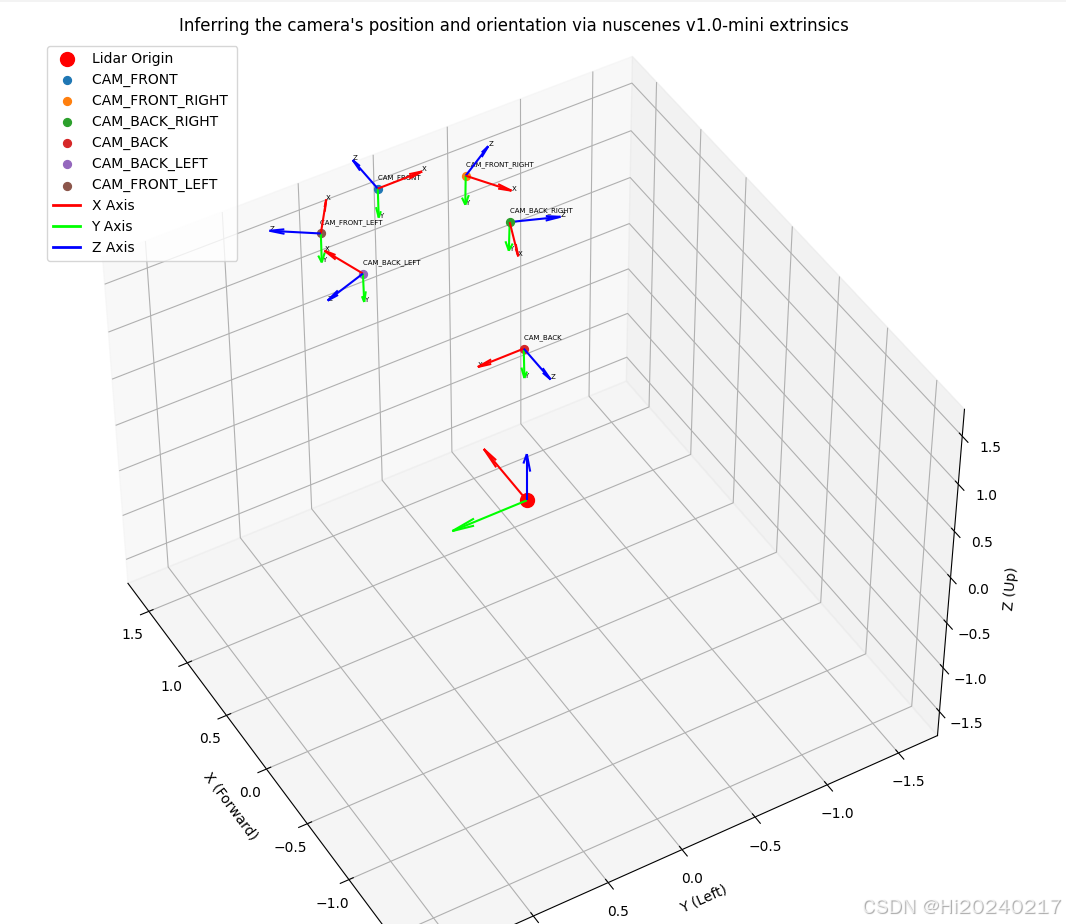
小结:
- X朝前: 因此该外参矩阵是相机到Lidar的变换
2. Apollo BEV模块外参可视化
import numpy as np
import matplotlib.pyplot as plt
from pyquaternion import Quaternion
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.lines import Line2D # 导入Line2D用于创建自定义图例
apollo_bev_kdata = np.array([
-1.40307297e-03, 9.07780395e-06, 4.84838307e-01, -5.43047376e-02,
-1.40780103e-04, 1.25770375e-05, 1.04126692e+00, 7.67668605e-01,
-1.02884378e-05, -1.41007011e-03, 1.02823459e-01, -3.07415128e-01,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 1.00000000e+00,
-9.39000631e-04, -7.65239349e-07, 1.14073277e+00, 4.46270645e-01,
1.04998052e-03, 1.91798881e-05, 2.06218868e-01, 7.42717385e-01,
1.48074005e-05, -1.40855671e-03, 7.45946690e-02, -3.16081315e-01,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 1.00000000e+00,
-7.0699735e-04, 4.2389297e-07, -5.5183989e-01, -5.3276348e-01,
-1.2281288e-03, 2.5626015e-05, 1.0212017e+00, 6.1102939e-01,
-2.2421273e-05, -1.4170362e-03, 9.3639769e-02, -3.0863306e-01,
0.0000000e+00, 0.0000000e+00, 0.0000000e+00, 1.0000000e+00,
2.2227580e-03, 2.5312484e-06, -9.7261822e-01, 9.0684637e-02,
1.9360810e-04, 2.1347081e-05, -1.0779887e+00, -7.9227984e-01,
4.3742721e-06, -2.2310747e-03, 1.0842450e-01, -2.9406491e-01,
0.0000000e+00, 0.0000000e+00, 0.0000000e+00, 1.0000000e+00,
5.97175560e-04, -5.88774265e-06, -1.15893924e+00, -4.49921310e-01,
-1.28312141e-03, 3.58297058e-07, 1.48300052e-01, 1.14334166e-01,
-2.80917516e-06, -1.41527120e-03, 8.37693438e-02, -2.36765608e-01,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 1.00000000e+00,
3.6048229e-04, 3.8333174e-06, 7.9871160e-01, 4.3321830e-01,
1.3671946e-03, 6.7484652e-06, -8.4722507e-01, 1.9411178e-01,
7.5027779e-06, -1.4139183e-03, 8.2083985e-02, -2.4505949e-01,
0.0000000e+00, 0.0000000e+00, 0.0000000e+00, 1.0000000e+00
])
cam_names = [
"CAM_FRONT",
"CAM_FRONT_RIGHT",
"CAM_FRONT_LEFT",
"CAM_BACK",
"CAM_BACK_LEFT",
"CAM_BACK_RIGHT"]
arrow_length_ratio=0.3
# 创建3D图形
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
# 车辆体坐标系原点
ax.scatter(0, 0, 0, c='r', s=100, label='Lidar Origin')
ax.quiver(0,0,0,0.3,0,0,color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0.3,0,color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0,0.3,color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
# 设置坐标轴范围
ax.set_xlim([-4, 4])
ax.set_ylim([-4, 4])
ax.set_zlim([-4, 4])
# 设置坐标轴标签
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title("Inferring the camera's position and orientation via bev_obstacle_detector k_data")
ext_params = apollo_bev_kdata.reshape(6, 4, 4)
for i, matrix in enumerate(ext_params):
# 提取数据
name = cam_names[i]
R = matrix[:3, :3] # 旋转矩阵
position = matrix[:3, 3] # 平移向量
# 绘制相机位置
ax.scatter(position[0], position[1], position[2], s=32, label=name)
arrow_length = 0.3
# 绘制相机坐标的Z轴(从原点向Z轴方向长1个单位的线)
# 1.将Z轴一个单位向量转换到世界坐标系
z_axis_unit_vector = np.array([0, 0, 1])
z_axis_unit_vector_w = R@z_axis_unit_vector
z_axis_unit_vector_w =z_axis_unit_vector_w* arrow_length
# 2.绘制朝向箭头
ax.quiver(
position[0], position[1], position[2],
z_axis_unit_vector_w[0],
z_axis_unit_vector_w[1],
z_axis_unit_vector_w[2],
color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+z_axis_unit_vector_w), "Z", fontsize=5)
arrow_length=200
# 绘制相机坐标的Y轴(从原点向Y轴方向长1个单位的线)
# 1.将Y轴一个单位向量转换到世界坐标系
y_axis_unit_vector = np.array([0, 1, 0])
y_axis_unit_vector_w = R@y_axis_unit_vector
y_axis_unit_vector_w = y_axis_unit_vector_w*arrow_length
# 2.绘制朝向箭
ax.quiver(
position[0], position[1], position[2],
y_axis_unit_vector_w[0],
y_axis_unit_vector_w[1],
y_axis_unit_vector_w[2],
color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+y_axis_unit_vector_w), "Y", fontsize=5)
# 绘制相机坐标的X轴(从原点向Y轴方向长1个单位的线)
# 1.将X轴一个单位向量转换到世界坐标系
x_axis_unit_vector = np.array([1, 0, 0])
x_axis_unit_vector_w = R@x_axis_unit_vector
x_axis_unit_vector_w = x_axis_unit_vector_w*arrow_length
# 2.绘制朝向箭头
ax.quiver(
position[0], position[1], position[2],
x_axis_unit_vector_w[0],
x_axis_unit_vector_w[1],
x_axis_unit_vector_w[2],
color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+x_axis_unit_vector_w), "X", fontsize=5)
# 添加相机名称标签
ax.text(position[0], position[1], position[2] + 0.1, name, fontsize=5)
# 添加坐标轴颜色图例
axis_legend_elements = [
Line2D([0], [0], color='red', lw=2, label='X Axis'),
Line2D([0], [0], color='lime', lw=2, label='Y Axis'),
Line2D([0], [0], color='blue', lw=2, label='Z Axis')
]
# 合并两个图例:相机位置图例 + 坐标轴颜色图例
handles, labels = ax.get_legend_handles_labels()
all_handles = handles + axis_legend_elements
# 添加合并后的图例
ax.legend(handles=all_handles, loc='upper left')
# 设置视角
ax.view_init(elev=25, azim=-60)
# 显示图形
plt.tight_layout()
plt.show()
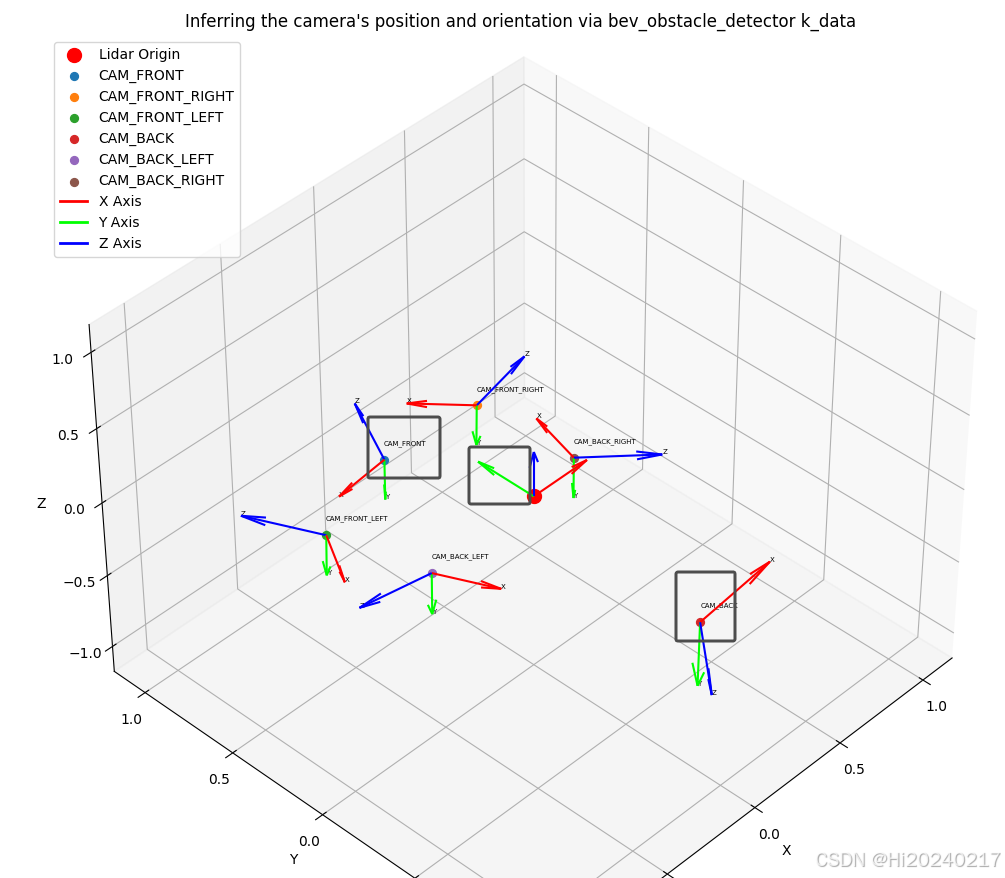
小结:
- Y轴朝前: 该变换是相机到车辆的变换
3. 单个相机外参可视化(front_6mm)
import numpy as np
import matplotlib.pyplot as plt
from pyquaternion import Quaternion
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.lines import Line2D # 导入Line2D用于创建自定义图例
import yaml
front_6mm_extrinsics='''
header:
seq: 0
frame_id: velodyne64
stamp:
nsecs: 0
secs: 0
child_frame_id: front_6mm
transform:
rotation:
w: 0.5
x: -0.5
y: 0.5
z: -0.5
translation:
x: 0.67
y: -0.1
z: -0.52
'''
config = yaml.load(front_6mm_extrinsics,Loader=yaml.FullLoader)
extrinsic=config['transform']
translation=extrinsic['translation']
rotation=extrinsic['rotation']
rotation=[rotation['w'], rotation['x'], rotation['y'], rotation['z']]
position=[translation['x'], translation['y'], translation['z']]
q = Quaternion(rotation)
R = q.rotation_matrix # 世界坐标系到相机坐标系的旋转
arrow_length_ratio=0.3
# 创建3D图形
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
# 车辆体坐标系原点
ax.scatter(0, 0, 0, c='r', s=100, label='Lidar Origin')
ax.quiver(0,0,0,0.3,0,0,color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0.3,0,color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.quiver(0,0,0,0,0,0.3,color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
# 设置坐标轴范围
ax.set_xlim([-4, 4])
ax.set_ylim([-4, 4])
ax.set_zlim([-4, 4])
# 设置坐标轴标签
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title("Inferring the camera's position and orientation via cam_extrinsics")
# 提取数据
name = "camera"
# 绘制相机位置
ax.scatter(position[0], position[1], position[2], s=32, label=name)
arrow_length = 0.3
# 绘制相机坐标的Z轴(从原点向Z轴方向长1个单位的线)
# 1.将Z轴一个单位向量转换到世界坐标系
z_axis_unit_vector = np.array([0, 0, 1])
z_axis_unit_vector_w = R@z_axis_unit_vector
z_axis_unit_vector_w =z_axis_unit_vector_w* arrow_length
# 2.绘制朝向箭头
ax.quiver(
position[0], position[1], position[2],
z_axis_unit_vector_w[0],
z_axis_unit_vector_w[1],
z_axis_unit_vector_w[2],
color='blue',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+z_axis_unit_vector_w), "Z", fontsize=5)
arrow_length=0.5
# 绘制相机坐标的Y轴(从原点向Y轴方向长1个单位的线)
# 1.将Y轴一个单位向量转换到世界坐标系
y_axis_unit_vector = np.array([0, 1, 0])
y_axis_unit_vector_w = R@y_axis_unit_vector
y_axis_unit_vector_w = y_axis_unit_vector_w*arrow_length
# 2.绘制朝向箭
ax.quiver(
position[0], position[1], position[2],
y_axis_unit_vector_w[0],
y_axis_unit_vector_w[1],
y_axis_unit_vector_w[2],
color='lime',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+y_axis_unit_vector_w), "Y", fontsize=5)
# 绘制相机坐标的X轴(从原点向Y轴方向长1个单位的线)
# 1.将X轴一个单位向量转换到世界坐标系
x_axis_unit_vector = np.array([1, 0, 0])
x_axis_unit_vector_w = R@x_axis_unit_vector
x_axis_unit_vector_w = x_axis_unit_vector_w*arrow_length
# 2.绘制朝向箭头
ax.quiver(
position[0], position[1], position[2],
x_axis_unit_vector_w[0],
x_axis_unit_vector_w[1],
x_axis_unit_vector_w[2],
color='red',arrow_length_ratio=arrow_length_ratio,linewidth=1.5)
ax.text(*(position+x_axis_unit_vector_w), "X", fontsize=5)
# 添加相机名称标签
ax.text(position[0], position[1], position[2] + 0.1, name, fontsize=5)
# 添加坐标轴颜色图例
axis_legend_elements = [
Line2D([0], [0], color='red', lw=2, label='X Axis'),
Line2D([0], [0], color='lime', lw=2, label='Y Axis'),
Line2D([0], [0], color='blue', lw=2, label='Z Axis')
]
# 合并两个图例:相机位置图例 + 坐标轴颜色图例
handles, labels = ax.get_legend_handles_labels()
all_handles = handles + axis_legend_elements
# 添加合并后的图例
ax.legend(handles=all_handles, loc='upper left')
# 设置视角
ax.view_init(elev=25, azim=-60)
# 显示图形
plt.tight_layout()
plt.show()

小结:
- X朝前: 因此该外参矩阵是相机到Lidar的变换
4. 坐标系变换验证:从旋转矩阵反推四元数
import numpy as np
from pyquaternion import Quaternion
'''
1. 定义基坐标系:X朝前, Y朝右, Z朝上
2. 新坐标系的单位向量在基坐标系中的表示为:
X_new = [0, -1, 0] # 基坐标系Y轴负方向
Y_new = [0, 0, -1] # 基坐标系Z轴负方向
Z_new = [1, 0, 0] # 基坐标系X轴正方向
'''
# 新坐标系的基向量在基坐标系中的表示
x_new_in_base = np.array([0, -1, 0])
y_new_in_base = np.array([0, 0, -1])
z_new_in_base = np.array([1, 0, 0])
# 构造旋转矩阵(每列为新坐标系的基向量)
rotation_matrix = np.column_stack((x_new_in_base, y_new_in_base, z_new_in_base))
# 使用旋转矩阵创建四元数
transform_quaternion = Quaternion(matrix=rotation_matrix)
# 获取四元数分量(pyquaternion 内部存储为 [w, x, y, z])
w, x, y, z = transform_quaternion
print("\n从新坐标系到基坐标系的变换四元数:")
print(f"w:{w} x:{x} y:{y} z:{z}")
输出(跟上面front_6mm_extrinsics中的rotation一致)
从新坐标系到基坐标系的变换四元数:
w:0.5 x:-0.5 y:0.5 z:-0.5
验证:与输入外参数据完全一致,确认了变换关系的正确性。