首先,啥是记忆化搜索呢?
记忆化搜索就是通过一个备忘录去记录多个完全相同子问题的结果,第一次遇到这个子问题时,就将这个子问题的结果记录在一个备忘录中,当下次遇到这个问题时,就直接去备忘录中找结果即可,其中备忘录可以是数组或者是一个哈希表
1.斐波那契数列
题目链接:509. 斐波那契数 - 力扣(LeetCode)
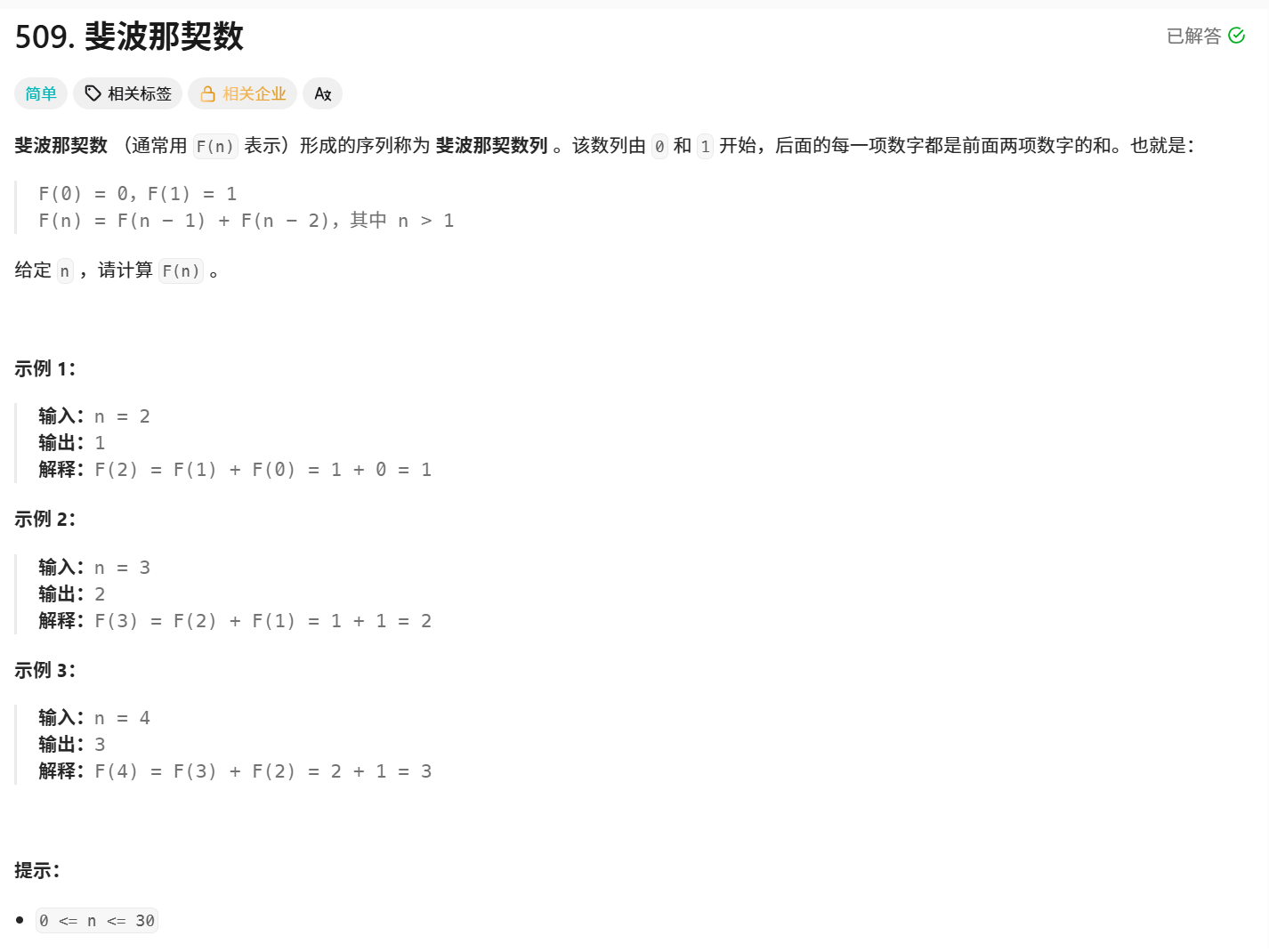
解法一:递归(暴搜)
代码实现:
class Solution {
public int fib(int n) {
return dfs(n);
}
public int dfs(int n){
if(n==0 || n==1) return n;
return dfs(n-1)+dfs(n-2);
}
}下图是其时间和空间复杂度
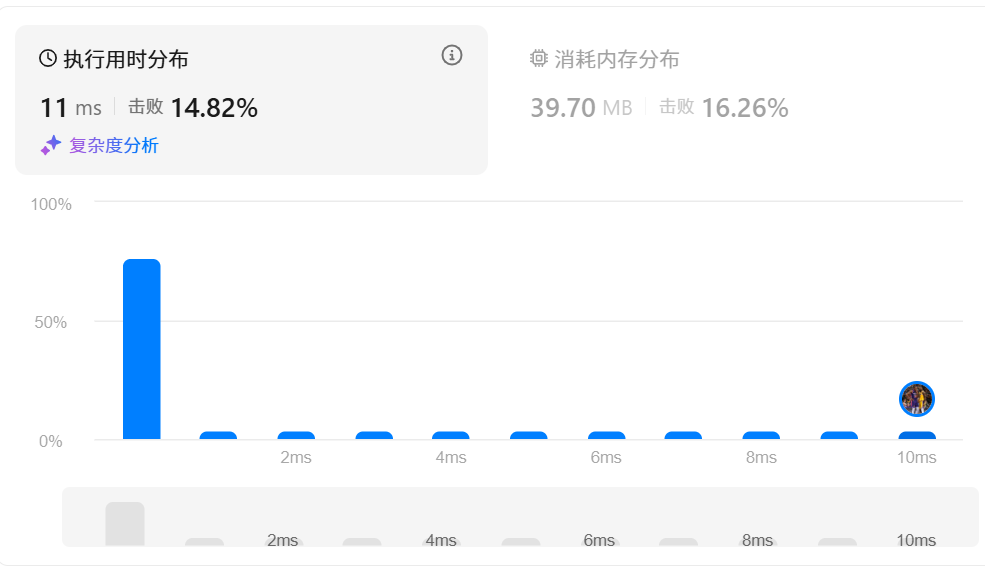
下图是递归时的过程图
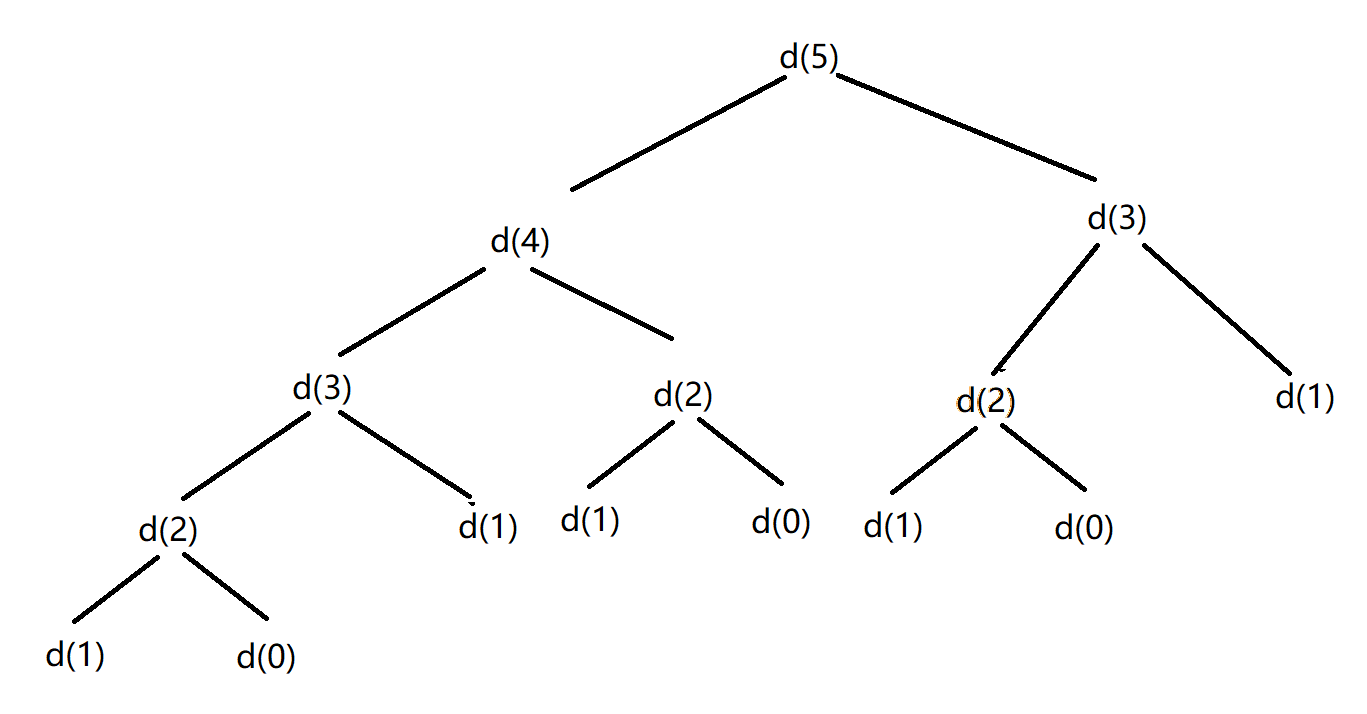
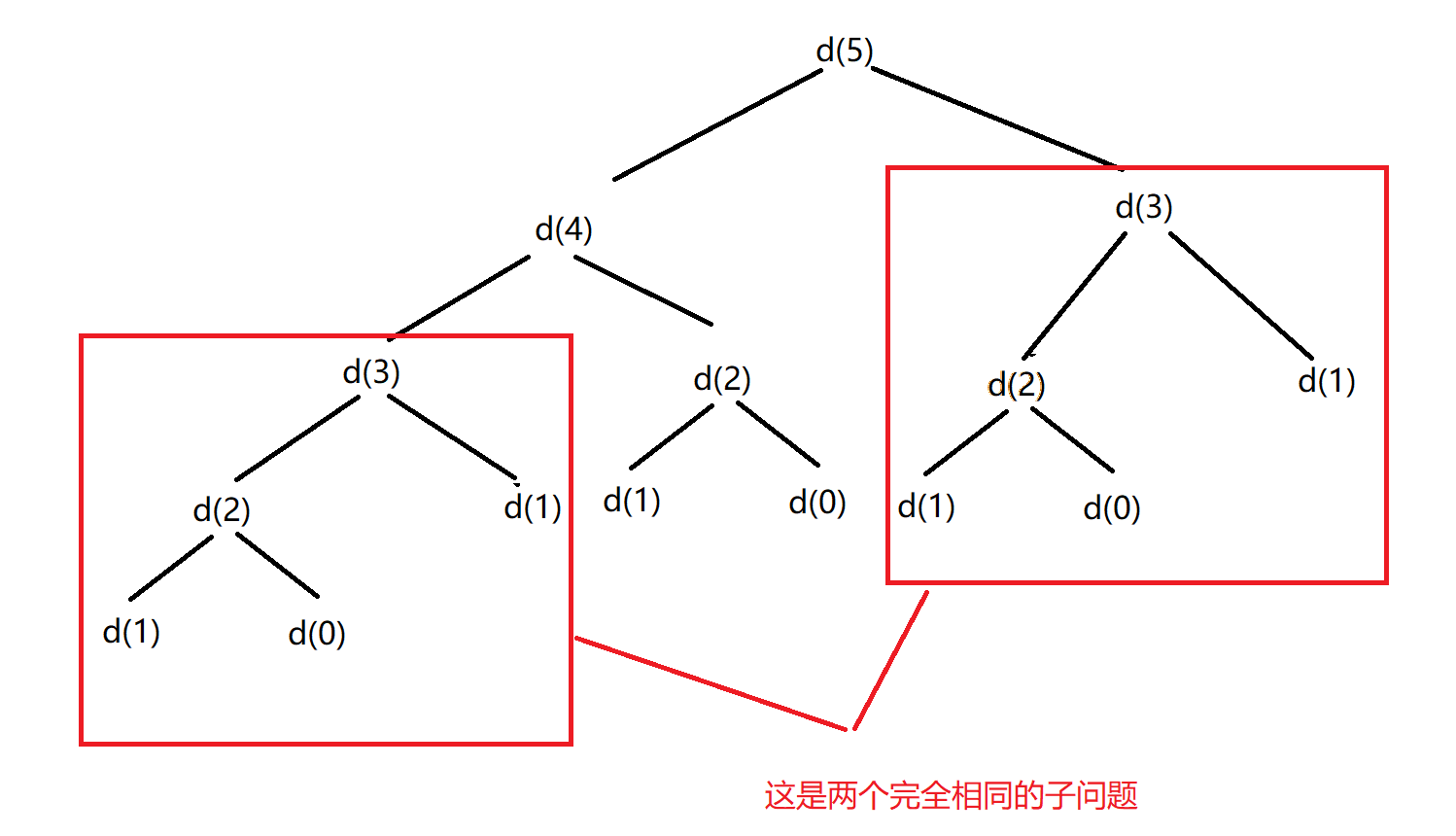
此时我们发现是有一些重复的子问题的,例如求d(3)的时候,两个求d(3)的子问题是完全相同的,此时就可以用一个备忘录将d(3)的结果存储起来,下次求d(3)时,直接从备忘录中寻找结果即可,然后以此类推
这就是我们所说的记忆化搜索,记忆化搜索也就是带备忘录的递归
代码如何实现记忆化搜索呢?
首先创建一个备忘录,可以是一个数组,也可以是一个哈希表,然后每次在递归函数返回前就玩被备忘录中插入结果,每次递归之前,就先查找一下备忘录有没有这个问题的结果,如果有就直接返回该结果
还有一个小细节:就是我们要对备忘录进行初始化,就是为了防止我都还没有解决这个问题,然而备忘录的默认值就有了这个问题的结果
代码实现:
class Solution {
int[] memo=new int[31];//创建备忘录
public int fib(int n) {
for(int i=0;i<31;i++) memo[i]=-1;//对备忘录初始化
return dfs(n);
}
public int dfs(int n){
if(memo[n]!=-1) return memo[n];//递归之前查找备忘录
//返回结果之前向备忘录中插入结果
if(n==0 || n==1){
memo[n]=n;
return memo[n];
}
memo[n]=dfs(n-1)+dfs(n-2);
return dfs(n-1)+dfs(n-2);
}
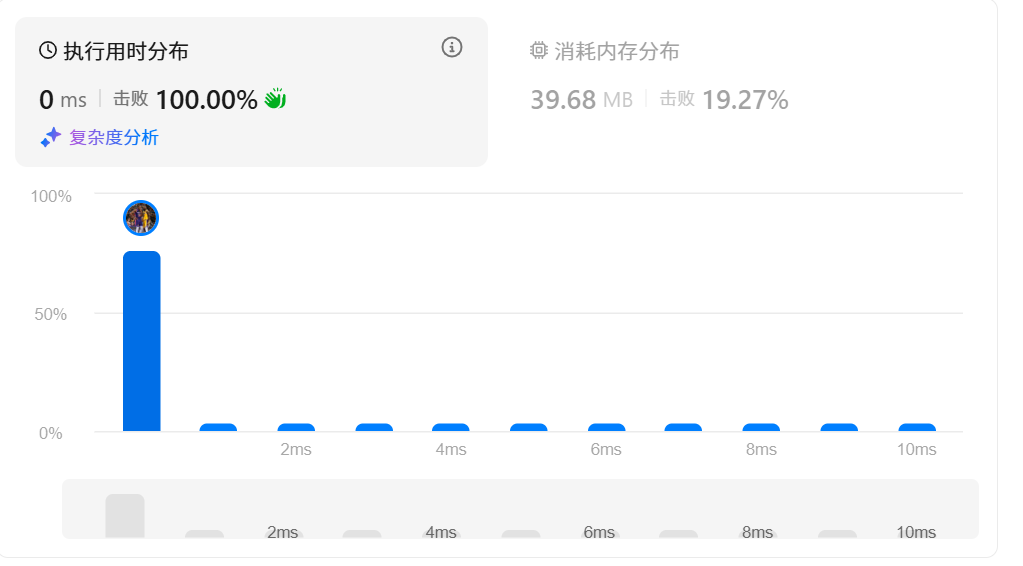
}时间空间复杂度如下图
2.不同路径

题目解析:计算并返回从起点有多少条路劲可以到达终点
算法讲解:
解法一:递归
因为一次自能向下或者向右移动一步,假设现在求的是从起点到(i,j)位置有多少条路劲可到达,首先就要知道从起点到达(i-1,j)有多少条路劲(用x来表示)或者从起点到达(i,j-1)有多少条路径(用y来表示),则此时从起点都到(i,j)位置的路径就有x+y条
递归出口的设计:如果i==0或者j==0,那么此时位置是非法的,此时到达(i,j)的路径个数就是0条,当i==0&&j==0时,也就是起点,此时到达起点的路劲就只有一条
代码实现:
class Solution {
public int uniquePaths(int m,int n){
return dfs(m,n);
}
public int dfs(int i,int j){
if(i==0 || j==0) return 0;
if(i==1 && j==1) return 1;
return dfs(i-1,j)+dfs(i,j-1);
}
}这个代码会超时,如下图
解法二:记忆化搜索
首先判断是否能用记忆化搜索呢?
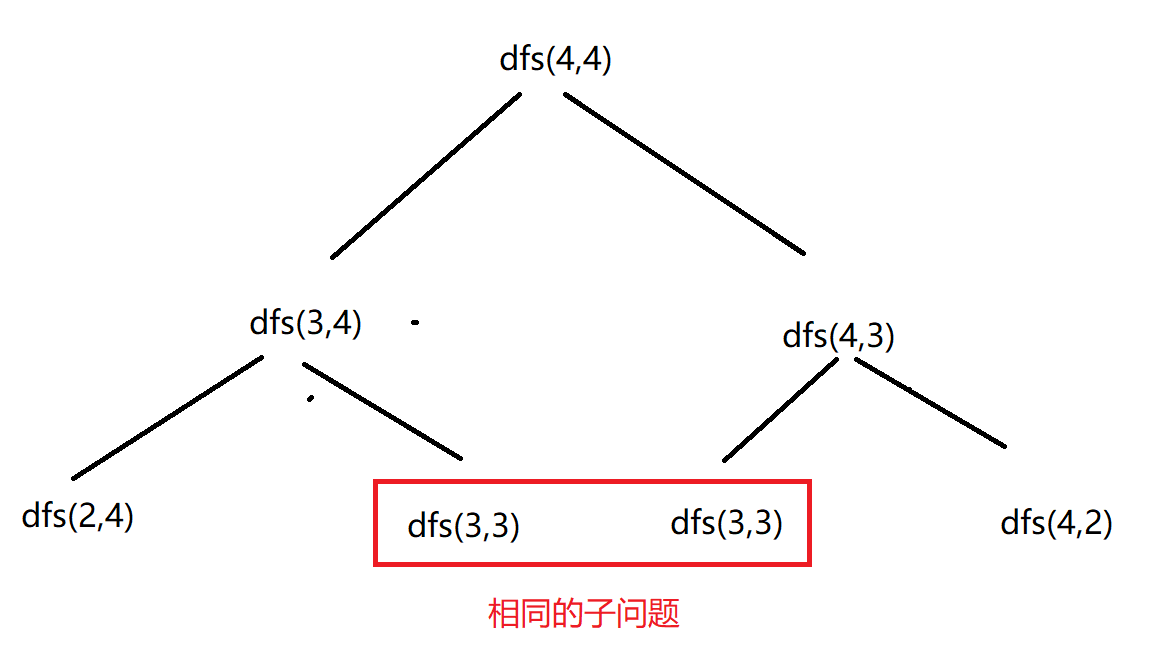
假设计算的是dfs(4,4),如下图,发现有相同的子问题,那么就可以使用记忆化搜索
代码实现:
此时就不用对备忘录进行初始化,对备忘录进行初始化的原因是要让备忘录一开始的值不能是结果中会出现的值,而此时0就是结果中不可能会出现的值,所以此时就没必要对备忘录进行初始化了
class Solution {
public int uniquePaths(int m,int n){
int[][] memo=new int[m+1][n+1];
return dfs(m,n,memo);
}
public int dfs(int m,int n,int[][] memo){
if(memo[m][n]!=0) return memo[m][n];
if(m==0 || n==0) return 0;
if(m==1&&n==1){
memo[m][n]=1;
return memo[m][n];
}
memo[m][n]=dfs(m,n-1,memo)+dfs(m-1,n,memo);
return memo[m][n];
}
}3.最长递增子序列
题目链接:300. 最长递增子序列 - 力扣(LeetCode)

题目解析:返回nums中最长递增子序列的长度
解法一:递归
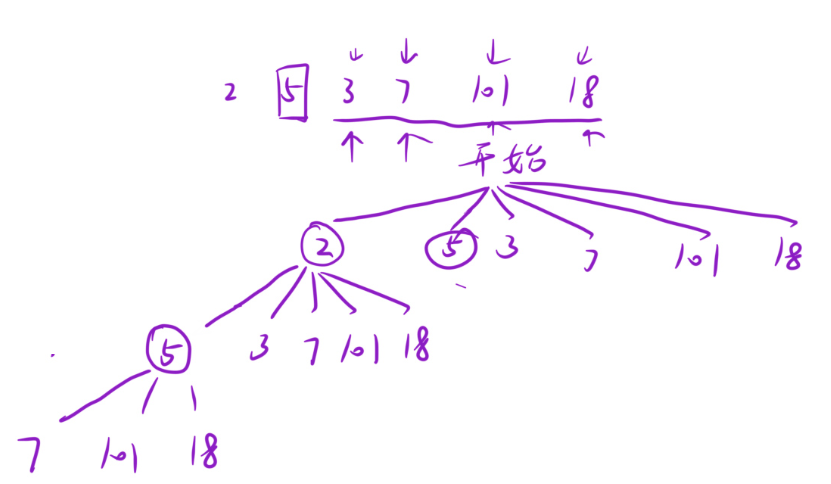
因为要求的是子序列,所以要尝试以nums中的每一个元素都作为子序列的第一个元素来分析问题,确立完子序列的第一个元素,接着就要尝试子序列的第二个位置上的元素,第二个位置也是要将除了选过的元素之外的其他元素都要试一遍,第三个位置的元素等等位置的元素也以此类推,如下图,画了部分情况
函数头的设计:因为要知道操作的是第几个元素,所以要传一个pos参数
代码实现:
下面的解法会超时
class Solution {
public int lengthOfLIS(int[] nums) {
int ret=0;
for(int i=0;i<nums.length;i++){
ret=Math.max(ret,dfs(nums,i));
}
return ret;
}
public int dfs(int[] nums,int pos){
int ret=1;
for(int i=pos+1;i<nums.length;i++){
if(nums[i]>nums[pos]){
ret=Math.max(ret,dfs(nums,i)+1);
}
}
return ret;
}
}解法二:记忆化搜索

如上图。就可以看出有一些重复的完全相同的子问题,此时就可以使用一个备忘录来记录这些重复问题的结果
代码实现:
一进入递归就先查一下备忘录,如果有对应的结果,此时直接返回结果即可
如果没有对应的结果,则就在递归返回结果前,向备忘录中添加对应的结果
class Solution {
int[] memo;//备忘录
public int lengthOfLIS(int[] nums) {
int ret=0;
memo=new int[nums.length];
for(int i=0;i<nums.length;i++){
ret=Math.max(ret,dfs(nums,i));
}
return ret;
}
public int dfs(int[] nums,int pos){
//查备忘录
if(memo[pos]!=0) return memo[pos];
int ret=1;
for(int i=pos+1;i<nums.length;i++){
if(nums[i]>nums[pos]){
ret=Math.max(ret,dfs(nums,i)+1);
}
}
//向备忘录中添加结果
memo[pos]=ret;
return ret;
}
}代码细节:
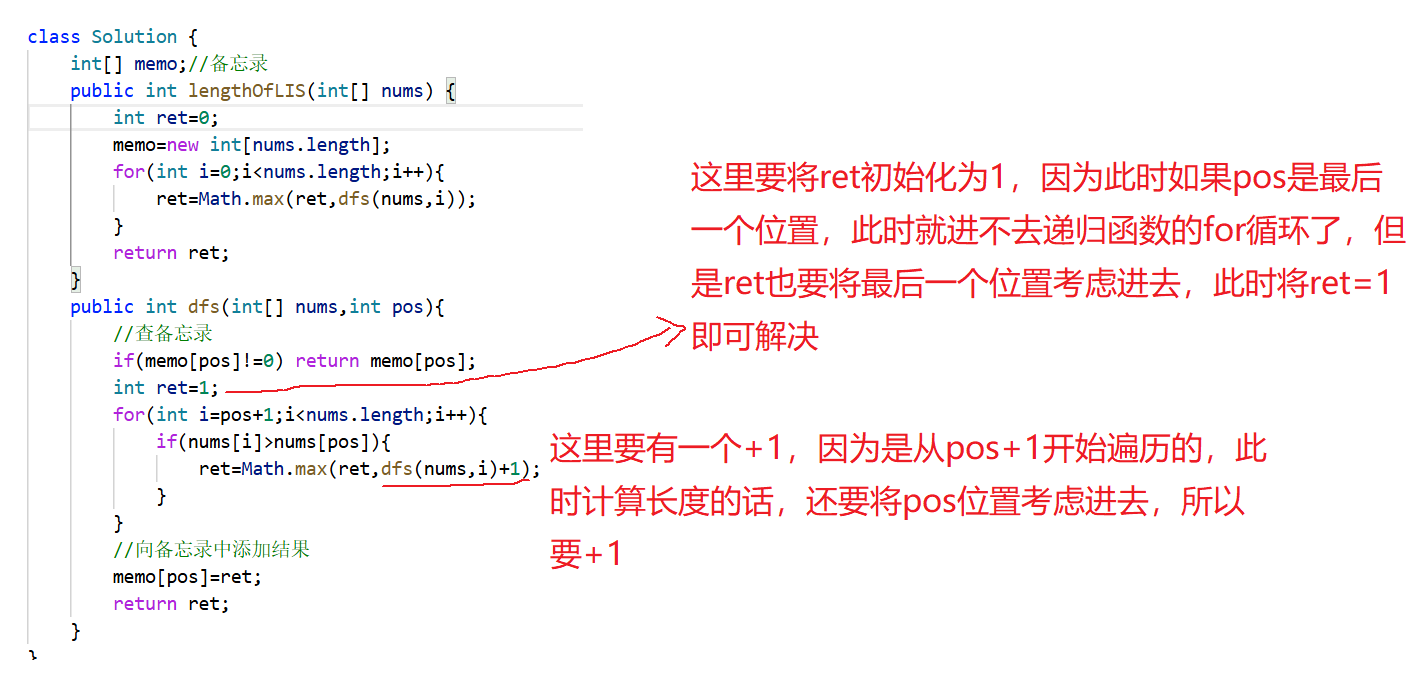
4.猜数字大小 II
题目链接:375. 猜数字大小 II - 力扣(LeetCode)

题目解析:进行猜数字,可以有很多种猜法,在每一种猜法中,都会有一个最大金额能保证无论在这种猜法中如何选择,都能保证这种猜法能够成功,在所有猜法中能够获胜的最小金额
算法讲解:记忆化搜索
不同的猜法就是第一个选择的数字不同,所以我们要枚举1~n的所有作为第一个选择的数字的情况,假设区间[1,10]
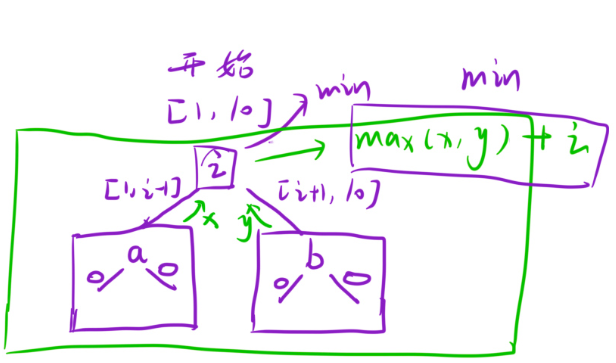
假设区间是[1,10],选择了某个数i之后,去i的两边搜索,因为i是有很多种情况的,则返回最小金额的情况即可
当以i为根节点时,处理完左右子数,左右子数分别返回一个金额数字x和y,x是能保证左子树能够才对的金额,y是能保证右子树能够猜对的金额,但是因为不知道要猜的数是哪一个,这个数有可能在左子数,也可能在右子树,所以此时要返回x和y中的最大值,保证要猜的数无论在那一边,都能够胜利,因为还要猜一个i,所以最后金额还要加上一个i
代码实现:
class Solution {
int[][] memo;
public int getMoneyAmount(int n) {
memo=new int[n+1][n+1];
return dfs(1,n);
}
public int dfs(int left,int right){
if(left>=right) return 0;
if(memo[left][right]!=0) return memo[left][right];
int ret=Integer.MAX_VALUE;
for(int head=left;head<=right;head++){//选择头节点
int x=dfs(left,head-1)+head;
int y=dfs(head+1,right)+head;
ret=Math.min(Math.max(x,y),ret);
}
memo[left][right]=ret;
return ret;
}
}5.矩阵中的最长递增路径
题目链接:329. 矩阵中的最长递增路径 - 力扣(LeetCode)

题目解析:返回矩阵中最长递增路径的长度
算法讲解:记忆化搜索
只需要对矩阵遍历一遍,遍历一个数字就上下左右的枚举,直到将所有情况都枚举出。
此时的dfs函数是用来计算遍历到某一个数字的的路径大小,此时不用对ret进行回溯,因为前面情况的ret也要和后面情况的ret表示,如果ret回溯了,那么后面的ret就无法和前面情况的原来的ret进行大小比较了
代码实现:
class Solution {
int h,l;
int[] dx={0,0,-1,1};
int[] dy={-1,1,0,0};
int[][] memo;
public int longestIncreasingPath(int[][] matrix) {
int ret=0;
h=matrix.length;
l=matrix[0].length;
memo=new int[h][l];
for(int i=0;i<h;i++){
for(int j=0;j<l;j++){
ret=Math.max(ret,dfs(matrix,i,j));
}
}
return ret;
}
public int dfs(int[][] matrix,int i,int j){
if(memo[i][j]!=0) return memo[i][j];
int ret=1;//每一条路径的最后一个数字进不去循环,要考虑这一个最后一个数字,此时只要将ret初始化为1即可
for(int k=0;k<4;k++){
int x=i+dx[k];
int y=j+dy[k];
if(x>=0 && x<h && y>=0 && y<l && matrix[x][y]>matrix[i][j]){
ret=Math.max(ret,dfs(matrix,x,y)+1);//这里+1是为将(i,j)位置这个点考虑上
}
}
memo[i][j]=ret;
return ret;
}
}