信息工程大学的出题依旧对待小白友好~在这里感谢出题方,但是你自己看看A题阴不阴😭
这次的题目没有很深奥的算法知识,大多都是一些模拟和常见的基础算法以及数论中的内容,所以我会认真对待这次的题目,补题会持续更新~
本场比赛传送门:河南萌新联赛2025第(五)场:信息工程大学”_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ
首当其冲的就是签到题了:
A - 宇宙终极能量调和与多维时空稳定性验证下的基础算术可行性研究
看到题目的我小脑都萎缩了,怀着反常的心思断定这道题就是签到题,点进去之后...哇,小脑变成大脑了!出题人你自己看看阴不阴😄:

这道题把我的思绪拉回到了高考做语文阅读理解的时候,读完一遍题发现读了一遍题,😄,但是看到别人一顿酷酷过,我第一眼就锁定了异或符号,直接将1 ^ 1的结果交了上去,没错!WA了,后来就放弃这一题了,谁爱写谁写,再之后看到更多的人过了,我还是咬咬牙又读了一遍题,终于发现了一些端倪:666经典线性叠加,我怀着幼儿园都会的1 + 1交了上去,过了...过的很窝囊

后来看题解,我想着出题人会给我一些说法,知道我看到了:
![]()
?我请问呢,全剧终。代码就不粘贴了,直接 cout << “ 2 ” << endl; 即可
接下来看B题:
B - 中位数
题目传送门:B-中位数_河南萌新联赛2025第(五)场:信息工程大学”
这道题还是朴实无华的简单思维题,只需要稍微动动脑就能发现,每次删除的是中位数,也就是说,不管对哪个长度为3的序列操作,最终都会剩下一个最小值和一个最大值,所以我们只需要对原数组进行排序,然后求最大值和最小值的中位数即可,不管了,直接交:

怎么错了?看一眼数据范围,哦哦哦哦哦!还有1的时候的特判!加上特判:

赛时代码如下:
// Problem: 中位数
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/B
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
void solve()
{
int n;cin>>n;vector<int> a(n+1);
if(n == 1)
{
cout<<n<<endl;
return ;
}
for(int i=1;i<=n;i++) cin>>a[i];
sort(a.begin() + 1,a.end());
int ans = a[1] + a[n];
ans /= 2;
cout<<ans<<endl;
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
C - 中位数 + 1
题目链接:C-中位数+1_河南萌新联赛2025第(五)场:信息工程大学”
这道题是很熟悉的一道题,通过每次加进来的一个数,然后计算出该数组中的中位数,说白了就是求动态中位数,直接套模版,用一个名为对顶堆的数据结构,对奇数和偶数情况进行判断,过过过
// Problem: 中位数+1
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/C
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
void solve()
{
priority_queue<int> da;//da
priority_queue<int,vector<int>,greater<int>> xiao;//xiao
int n;cin>>n;
for(int i=1;i<=n;i++)
{
int x;cin>>x;
da.push(x);
if(da.size() == xiao.size() + 2)
{
int t = da.top();da.pop();
xiao.push(t);
}
while(xiao.size() && da.top() > xiao.top())
{
int t = da.top();da.pop();
int tt = xiao.top();xiao.pop();
da.push(tt);
xiao.push(t);
}
if(i & 1) cout<<da.top()<<' ';
else if(da.size() && xiao.size()) cout<<(da.top() + xiao.top())/2<<' ';
}
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
F - 中位数 + 4
题目链接:F-中位数+4_河南萌新联赛2025第(五)场:信息工程大学”
这道题就是将给定的数转化为k进制,然后判断有几个后导零即可,直接用字符串模拟即可。
// Problem: 中位数+4
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/F
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
string to(int n,int k)
{
string ans;int t = k;
while(n)
{
string t = to_string(n%k);
n /= k;
ans += t;
}
reverse(ans.begin(),ans.end());
return ans;
}
void solve()
{
int n,k;cin>>n>>k;
string s = to(n,k);
int cnt = 0;
for(int i=s.size()-1;i>0;i--)
{
if(s[i] == '0') cnt ++;
else break;
}
cout<<cnt<<endl;
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
G - 简单题
题目链接:G-简单题_河南萌新联赛2025第(五)场:信息工程大学”
幸亏我会三阶行列式,将三阶行列式算出来之后就是1 1 2 3,相信一直刷算法的小伙伴对这个序列都不陌生吧,这不就是斐波那契数列吗??!,然后通过打表找出斐波那契数列的和的奇偶性的变化是奇偶偶奇偶偶奇偶偶奇...所以我们只需要对n--,然后对3取模就行了。
// Problem: 简单题
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/G
// Memory Limit: 2048 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
void solve()
{
// int n;cin>>n;
// int sum;n--;
// sum = (1 + n) * n / 2;
// sum ++;
// cout<<sum % 2<<endl;
// vector<int> a(20,0);
// a[1] = 1;
// a[2] = 1;
// a[3] = 2;
// for(int i=4;i<=17;i++) a[i] = a[i-1] + a[i-2];
// for(int i=1;i<=17;i++) a[i] = a[i] + a[i-1];
// for(int i=1;i<=17;i++) cout<<a[i] % 2<<endl;
int n;cin>>n;
if(n == 1)
{
cout<<1<<endl;
}
else
{
n--;
if(n % 3 == 0) cout<<1<<endl;
else cout<<0<<endl;
}
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
K - 狂飙追击
题目链接:K-狂飙追击_河南萌新联赛2025第(五)场:信息工程大学”
这道题唯一需要注意的就是题目中说的m是动态变化的,不是根据初始的位置而确定的(就是因为这个导致错了好几次),明白这里之后就很好想了,我们只需要用一个搜索都能出来,这里用BFS和DFS都可以,我下面就以DFS来举例子吧:
// Problem: 狂飙追击
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/K
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
int endx,endy,dis = inf;
bool f = 0;
void dfs(int x,int y,int st)
{
if(x > endx || y > endy) return ;
if(x == endx && y == endy)
{
f = 1;
dis = min(dis,st);
return ;
}
int m = max(x,y);
int tx = x + m;
int ty = y + m;
dfs(tx,y,st + 1);
dfs(x,ty,st + 1);
}
void solve()
{
int a,b;cin>>a>>b>>endx>>endy;
dfs(a,b,0);
if(f) cout<<dis<<endl;
else cout<<"-1"<<endl;
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
由于测试样例比较水,导致我直接把这道题用正向搜索卡过去了,所以下面就来给出正确的代码,我们只需要逆序就行了,因为逆序的话路线就是固定的那一条了。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
void solve() {
int sx,sy,tx,ty;
cin>>sx>>sy>>tx>>ty;
int ans=0;
while(tx!=sx||ty!=sy)
{
if(tx<sx||ty<sy)
{
cout<<-1<<endl;
return;
}
if(tx==ty)//样例中有一方为0的情况
{
if(sy>0) tx=0;
else ty=0;
ans++;
continue;
}
if(tx<ty)
{
swap(tx,ty);
swap(sx,sy);
}
if(tx>2*ty)//原先“tx”是最大的 在“x”方向上移动了
{
if(tx%2!=0)
{
cout<<-1<<endl;
return;
}
tx/=2;
}
else tx-=ty;//在另一个方向上移动了
ans++;
}
cout<<ans<<endl;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int T = 1;
while (T--) solve();
return 0;
}I - Re:从零开始的近世代数复习(easy)
题目链接:I-Re:从零开始的近世代数复习(easy)_河南萌新联赛2025第(五)场:信息工程大学”
这道题一开始看到节点之间有这依赖的顺序关系,以为这个是用拓扑排序写的,后来读完题之后发现是一个树形结构,所以这道题可以用倍增优化LCA来写!但是赛时改了好几次都错了,没办法只能在赛后补题了。对倍增求LCA不熟悉的可以看这里:倍增求LCA 详解见代码:
// Problem: Re:从零开始的近世代数复习(easy)
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/I
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
const int N = 1e5 + 10;
vector<int> e[N];
vector<int> dep(N);
int f[N][25],g[N][25];//g[x][i]表示的是从节点x开始跳2^i步的路径上的权值之和(不包括目标节点)
int ans = 0;
void dfs(int x,int fa)
{
f[x][0] = fa;
dep[x] = dep[fa] + 1;//存每一个节点的深度 用于在之后的判断两个节点是否在同一层
for(int i=1;i<25;i++)
{
f[x][i] = f[f[x][i-1]][i-1];//记录x节点的第2^i级祖先
g[x][i] = g[f[x][i-1]][i-1] + g[x][i-1];//记录x节点跳2^i级之后路径上的权值(在g[x][i-1]的基础上累加当前节点)
}
for(auto &i : e[x]) dfs(i,x);
}
int LCA(int x,int y)
{
if(dep[x] < dep[y]) swap(x,y);//不在同一层的处理
for(int i=24;i>=0;i--)
{
if(dep[f[x][i]] >= dep[y])//注意先更新ans,再更新x
ans += g[x][i],x = f[x][i];//跳到同一层过程中所需要花费的代价
}
if(x == y) return x;//同一个节点就说明当前节点就是LCA
for(int i=24;i>=0;i--)//倍增找LCA
{
if(f[x][i] != f[y][i])
{
ans += g[x][i] + g[y][i];//注意先更新ans 再更新x和y
x = f[x][i];
y = f[y][i];
}
}
ans += g[x][0] + g[y][0];//最后的两个节点是在LCA的下一层 所以再加上当前节点所需要花费的代价
return f[x][0];
}
void solve()
{
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>g[i][0];
for(int i=1;i<n;i++)
{
int u,v;cin>>u>>v;
e[u].push_back(v);
}
dfs(1,0);int q;cin>>q;
while(q--)
{
int k;cin>>k;int x,y;cin>>x>>y;
ans = g[1][0];//每次询问一开始就先将根节点赋值给ans
int lca = LCA(x,y);//计算x和y的最近公共祖先
if(lca != 1) LCA(lca,1);//如果最近公共祖先不是根节点的话,我们还需要在根节点的前提下,所以要加上这一段之间的权值
cout<<ans<<endl;
}
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
H - 简单题 +
题目链接:H-简单题+_河南萌新联赛2025第(五)场:信息工程大学”
这道题考察到了一个名为《矩阵快速幂》的内容,好吧,我承认我属实是孤陋寡闻了,之前只用到过快速幂的算法,这是我第一次接触到矩阵快速幂:
对于斐波那契数列来说,他的前n项和与他的第n+2项斐波那契数有着这样的关系:
S(N) = F(N + 2) - 1所以我们求斐波那契数列的前n项和的问题就转变为了求斐波那契数列的第n + 2项,然后对mod取模就行了,然而对于斐波那契数列的求解来说,用O(n)的时间复杂度对于1e9的样例来说肯定是过不了的,所以就用到了矩阵快速幂的算法:
观察斐波那契数列: 0 1 1 2 3 5 8 ......
如果我们将0 1视为一个矩阵的话,那么我们就可以让这个矩阵与一个二维的矩阵相乘得到的矩阵就是1 1,然后我们就可以得到斐波那契数列的转化矩阵就是(0 1 1 1)即左上角为0其余位置为1的一个矩阵,(其实记住就行了,因为这个转换矩阵仅仅对于求斐波那契数列有效),所以我们就对这个矩阵做快速幂操作就能求出这个矩阵的高次幂,也就是第n项斐波那契数列了。因为斐波那契数列的第一项为1,而我们的矩阵快速幂是从01开始算的,算出来的第一项就为1 1,这是后下面的位置求的就是第2项斐波那契数了,而我们此时需要的是第一项(n == 1),所以我们可以在fab函数中返回右上角的那个数,当然我们也可以在输入的n的时候对n--,然后返回右下角的那个值即可,这个题也算是仅限于求斐波那契数列的第n项了。
// Problem: 简单题+
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/H
// Memory Limit: 2048 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
#define MOD %mod
#define vvector vector<vector<int>>
const int mod = 998244353;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
vvector kksm(const vvector& m1,const vvector& m2)
{
int x = m1.size(),y = m2[0].size(),f = m1[0].size();
vvector res(x,vector<int>(y,0));//构建一个x行y列的矩阵
for(int i=0;i<x;i++)
{
for(int j=0;j<y;j++)
{
int sum = 0;
for(int k=0;k<f;k++) sum = (sum + m1[i][k] MOD * m2[k][j] MOD) MOD;
res[i][j] = sum;
}
}
return res ;
}
int fab(int n)
{
if(n < 0) return 0;
vvector m = {{0,1},{1,1}};//M矩阵
vvector res = {{1,0},{0,1}};
while(n > 0)
{
if(n & 1) res = kksm(res,m);
m = kksm(m,m);
n >>= 1LL;
}
return res[0][1] MOD;
}
void solve()
{
int n;cin>>n;
int F = fab(n + 2) - 1;
cout<<F<<endl;
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
当然更直观的理解就是:
对于n来说,我们求的是第n项斐波那契数,我们就需要对(0 1)矩阵与(0 1 1 1)矩阵的n-1次幂做乘积,所以我们要对输入的n--,然后返回的值是乘积之后的矩阵中的右下角的值
即:
// Problem: 简单题+
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/H
// Memory Limit: 2048 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
#define MOD %mod
#define vvector vector<vector<int>>
const int mod = 998244353;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
vvector kksm(const vvector& m1,const vvector& m2)
{
int x = m1.size(),y = m2[0].size(),f = m1[0].size();
vvector res(x,vector<int>(y,0));//构建一个x行y列的矩阵
for(int i=0;i<x;i++)
{
for(int j=0;j<y;j++)
{
int sum = 0;
for(int k=0;k<f;k++) sum = (sum + m1[i][k] MOD * m2[k][j] MOD) MOD;
res[i][j] = sum;
}
}
return res ;
}
int fab(int n)
{
if(n < 0) return 0;
vvector m = {{0,1},{1,1}};//M矩阵
vvector res = {{1,0},{0,1}};
while(n > 0)
{
if(n & 1) res = kksm(res,m);
m = kksm(m,m);
n >>= 1LL;
}
return res[1][1] MOD;
}
void solve()
{
int n;cin>>n;n--;
int F = fab(n + 2) - 1;
cout<<F<<endl;
// cout<<fab(n)<<endl;
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
L - 防K题
题目链接:L-防k题_河南萌新联赛2025第(五)场:信息工程大学”
依旧被题目名字吓的没有勇气看这道题.....题目中问你需要最少的咔咔的数量,那么我们直接用二分答案模拟就行了,check函数也很好实现!需要注意的是x1,y1是标准库中的全局变量不能直接用不然会编译错误的😭😭😭
// Problem: 防k题
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/L
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
#define T return true;
#define F return false;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
int x_1,y_1,z,x2,y2;
bool check(int mid)
{
int x = x_1;//咔咔的血量
int k = y_1;//咔咔的攻击力
int y = x2;//战士的血量
while(true)
{
if(mid <= 0) F//咔咔没了 false
if(y <= 0) T//战士没了 true
for(int i=1;i<=3;i++)
{
x -= y2;//其中一只咔咔被攻击
if(x <= 0) mid--,x = x_1;//死了一只咔咔 换另一只咔咔
}
y -= k * mid;//轮到咔咔攻击了 战士受到的攻击力为咔咔的数量 * 咔咔的现在的攻击力
k += z;//咔咔在这一回合结束后会增加z的攻击力
}
}
void solve()
{
cin>>x_1>>y_1>>z>>x2>>y2;
int l = 0,r = inf;
while(l < r)
{
int mid = (l + r) >> 1LL;
if(check(mid)) r = mid;
else l = mid + 1LL;
}
cout<<r<<endl;
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int _=1;
// cin>>_;
while(_--) solve();
return 0;
}
E - 中位数 + 3
题目链接:E-中位数+3_河南萌新联赛2025第(五)场:信息工程大学”
这道题也是一道数论中的内容,题解中给出的数论公式为:
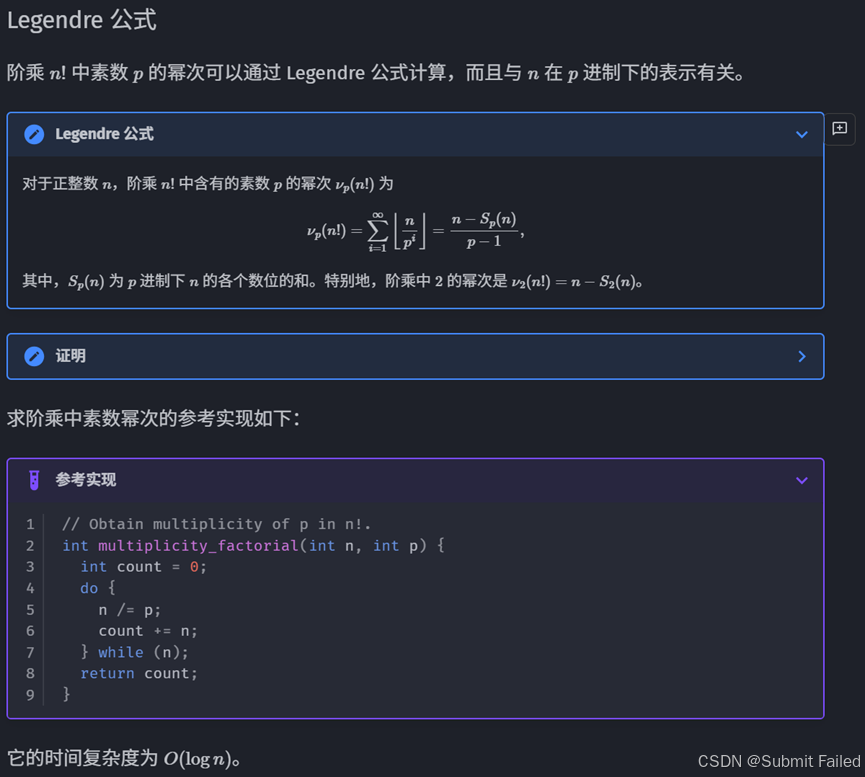
这个公式求的是:n!中p因子的个数可计算。故分解k求结果取最小即可;
// Problem: 中位数+3
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/115567/E
// Memory Limit: 2048 MB
// Time Limit: 20000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
const int INF = 0x3f3f3f3f;
const int inf = 1e18;
/*
算法思路:
1. 将k分解质因数,得到所有质因数及其指数
2. 对每个质因数d,计算它在n!中出现的总次数s
- 计算方法:s = floor(n/d) + floor(n/d^2) + floor(n/d^3) + ...
3. 对于每个质因数d,计算s/v(v是d在k中的指数)
4. 所有s/v的最小值就是n!在k进制下的后置零个数
*/
//基于数论知识,k进制下n!的后置零个数等于各质因数在n!中出现次数除以其在k中指数的最小值
void solve()
{
int n,k;cin>>n>>k;vector<pii> a;//存储质因数及其指数
for(int i=2;i*i<=k;i++)
{
if(k % i == 0)//试除法分解质因数
{
int cnt = 0;
while(k % i == 0)//计算当前质因数的指数
{
k /= i;
cnt ++;
}
a.push_back({i,cnt});//存储质因数及其指数
}
}
if(k) a.push_back({k,1LL});//处理大质数情况
int res = inf;
for(auto &i : a)//计算每个质因数在n!中出现的次数
{
int x = i.fi;
int y = i.se;//x是质因数,y是其在k中的指数
int sum = 0,t = n;//计算x在n!中的总出现次数
while(t)
{
sum += t / x;//累计当前层的贡献
t /= x;//进入下一层
}
res = min(res,sum / y);//取所有质因数中的最小值
}
cout<<res<<endl;
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
}
