1.简介
文章解决了球形多飞行器路径规划问题(SMAPPP),该问题旨在模拟未来探索地外行星或导弹轨迹的航天器路径规划研究。差分进化(DE)算法是一种经典的元启发式算法,应用于SMAPPP时不会产生令人满意的结果。受DE全局和局部搜索能力不平衡的约束,本文提出了一种自适应更新策略差分进化算法(SaUSDE),以增强其求解全局优化问题的性能。SaUSDE算法融合了四种截然不同的DE变体策略。在这些策略中,算法自适应且频繁地针对不同问题选择更合适的策略,从而有效地平衡全局和局部搜索能力。与这些高级算法相比,所提出的算法总体上取得了优越的结果。最后,将SaUSDE应用于模拟球形多飞行器路径规划问题。在涉及3到12架飞机的场景中,SaUSDE算法有效地避免了每架飞机与某些禁飞区(静态障碍物)以及未知飞行物体(动态障碍物)之间的碰撞。
2. 预备知识
2.1. 差分进化算法
差分进化(Differential Evolution, DE)是一种经典的元启发式算法。其流程包括种群的随机初始化,随后每个个体经历三个进化过程:变异、交叉和选择。
(1) 变异
在DE中,变异策略涉及从种群中随机选择两个个体,缩放其位置向量的差值,并将该缩放差值作为更新目标个体位置的步长。数学表达式如下:
yij=xij+F⋅(xr1j−xr2j),i=1,2,…,N(1) y_{ij} = x_{ij} + F \cdot (x_{r1j} - x_{r2j}), \quad i=1,2,\dots,N \tag{1} yij=xij+F⋅(xr1j−xr2j),i=1,2,…,N(1)
其中xix_ixi表示种群中第iii个个体,xr1x_{r1}xr1和xr2x_{r2}xr2是从种群中随机选择的两个不同个体,jjj表示解的第jjj维,FFF为缩放因子。
(2) 交叉
交叉策略通过交换变异个体yiy_iyi与目标个体xix_ixi的第jjj维分量,生成新个体ziz_izi。数学表达式为:
zij={yij,如果 r≤CR 或 j=jrxij,否则(2) z_{ij} = \begin{cases} y_{ij}, & \text{如果 } r \leq CR \text{ 或 } j = j_r \\ x_{ij}, & \text{否则} \end{cases} \tag{2} zij={yij,xij,如果 r≤CR 或 j=jr否则(2)
其中CRCRCR为交叉率,jrj_rjr为随机选择的维度编号,rrr为区间[0,1][0,1][0,1]内的随机数。
(3) 选择
在选择过程中,比较目标个体XiX_iXi与交叉个体ZiZ_iZi的适应度值,保留适应度更优的个体作为下一代的位置向量:
Xi′={Zi,如果 F(Zi)<F(Xi)Xi,否则(3) X_i' = \begin{cases} Z_i, & \text{如果 } F(Z_i) < F(X_i) \\ X_i, & \text{否则} \end{cases} \tag{3} Xi′={Zi,Xi,如果 F(Zi)<F(Xi)否则(3)
其中F(Zi)F(Z_i)F(Zi)和F(Xi)F(X_i)F(Xi)分别表示交叉个体和目标个体的适应度值。
2.2. 现实约束优化问题
本文选取了CEC2020中的48个现实约束优化问题,涵盖工业化学过程、合成与设计、机械工程、电力系统、电力电子和牲畜饲料配比优化等领域。问题定义如下:
最小化 f(X),X=(x1,x2,…,xd)(4) \text{最小化 } f(X), \quad X = (x_1, x_2, \dots, x_d) \tag{4} 最小化 f(X),X=(x1,x2,…,xd)(4)
约束条件为:
{gi(X)≤0,i=1,…,nhj(X)=0,j=n+1,…,m \begin{cases} g_i(X) \leq 0, & i=1, \dots, n \\ h_j(X) = 0, & j=n+1, \dots, m \end{cases} {gi(X)≤0,hj(X)=0,i=1,…,nj=n+1,…,m
其中XXX为解向量,ggg表示不等式约束,nnn为不等式约束数量,hhh为等式约束,mmm为总约束条件数。
2.3. 球形多飞行器路径规划模型
球形多飞行器路径规划(SMAPPP)是一个最小化问题,其目标是在球形空间中导航多个飞行器,避开禁飞区和未知飞行物,保持与其他飞行器的安全距离,并以最小成本逐步到达目的地。每个飞行器被建模为均匀圆形,其位置更新公式为:
{xt=xt−1+vt⋅sin(θt)⋅cos(ϕt)yt=yt−1+vt⋅sin(θt)⋅sin(ϕt)zt=zt−1+vt⋅cos(θt)(5) \begin{cases} x_t = x_{t-1} + v_t \cdot \sin(\theta_t) \cdot \cos(\phi_t) \\ y_t = y_{t-1} + v_t \cdot \sin(\theta_t) \cdot \sin(\phi_t) \\ z_t = z_{t-1} + v_t \cdot \cos(\theta_t) \end{cases} \tag{5} ⎩ ⎨ ⎧xt=xt−1+vt⋅sin(θt)⋅cos(ϕt)yt=yt−1+vt⋅sin(θt)⋅sin(ϕt)zt=zt−1+vt⋅cos(θt)(5)
约束条件为:
vmin≤vt≤vmax(6) v_{\text{min}} \leq v_t \leq v_{\text{max}} \tag{6} vmin≤vt≤vmax(6)
其中(xt,yt,zt)(x_t, y_t, z_t)(xt,yt,zt)为飞行器在时间ttt的三维坐标,vtv_tvt为单位时间飞行速度,θt\theta_tθt和ϕt\phi_tϕt分别为偏转的极角和方位角。适应度函数定义为:
最小化 Fit=F1+F2+F3+F4(7) \text{最小化 } Fit = F_1 + F_2 + F_3 + F_4 \tag{7} 最小化 Fit=F1+F2+F3+F4(7)
F1F_1F1(剩余距离):
F1=∑i=1NA(fi+gi)(8) F_1 = \sum_{i=1}^{NA} (f_i + g_i) \tag{8} F1=i=1∑NA(fi+gi)(8)
其中:
fi=(xid−xic)2+(yid−yic)2+(zid−zic)2(9) f_i = \sqrt{(x_i^d - x_i^c)^2 + (y_i^d - y_i^c)^2 + (z_i^d - z_i^c)^2} \tag{9} fi=(xid−xic)2+(yid−yic)2+(zid−zic)2(9)
gi={ζ,如果 Di>R0,否则(10) g_i = \begin{cases} \zeta, & \text{如果 } D_i > R \\ 0, & \text{否则} \end{cases} \tag{10} gi={ζ,0,如果 Di>R否则(10)
DiD_iDi为第iii个飞行器到球心的距离:
Di=(xic)2+(yic)2+(zic)2(11) D_i = \sqrt{(x_i^c)^2 + (y_i^c)^2 + (z_i^c)^2} \tag{11} Di=(xic)2+(yic)2+(zic)2(11)F2F_2F2(禁飞区避障):
F2={∑i=1NAdi1,如果 di1<ds0,否则(12) F_2 = \begin{cases} \sum_{i=1}^{NA} d_i^1, & \text{如果 } d_i^1 < d_s \\ 0, & \text{否则} \end{cases} \tag{12} F2={∑i=1NAdi1,0,如果 di1<ds否则(12)
其中di1d_i^1di1为第iii个飞行器到所有禁飞区的距离和:
di1=∑j=1NS(xic−xjf)2+(yic−yjf)2+(zic−zjf)2(13) d_i^1 = \sum_{j=1}^{NS} \sqrt{(x_i^c - x_j^f)^2 + (y_i^c - y_j^f)^2 + (z_i^c - z_j^f)^2} \tag{13} di1=j=1∑NS(xic−xjf)2+(yic−yjf)2+(zic−zjf)2(13)F3F_3F3(未知飞行物避障):
F3={∑i=1NAdi2,如果 di2<ds0,否则(14) F_3 = \begin{cases} \sum_{i=1}^{NA} d_i^2, & \text{如果 } d_i^2 < d_s \\ 0, & \text{否则} \end{cases} \tag{14} F3={∑i=1NAdi2,0,如果 di2<ds否则(14)
其中di2d_i^2di2为第iii个飞行器到所有未知飞行物的距离和:
di2=∑j=1ND(xic−xjo)2+(yic−yjo)2+(zic−zjo)2(15) d_i^2 = \sum_{j=1}^{ND} \sqrt{(x_i^c - x_j^o)^2 + (y_i^c - y_j^o)^2 + (z_i^c - z_j^o)^2} \tag{15} di2=j=1∑ND(xic−xjo)2+(yic−yjo)2+(zic−zjo)2(15)
未知飞行物的位置更新为:
{xjo=xjo+vjo⋅sin(θjo)⋅cos(ϕjo)yjo=yjo+vjo⋅sin(θjo)⋅sin(ϕjo)zjo=zjo+vjo⋅cos(θjo)(16) \begin{cases} x_j^o = x_j^o + v_j^o \cdot \sin(\theta_j^o) \cdot \cos(\phi_j^o) \\ y_j^o = y_j^o + v_j^o \cdot \sin(\theta_j^o) \cdot \sin(\phi_j^o) \\ z_j^o = z_j^o + v_j^o \cdot \cos(\theta_j^o) \end{cases} \tag{16} ⎩ ⎨ ⎧xjo=xjo+vjo⋅sin(θjo)⋅cos(ϕjo)yjo=yjo+vjo⋅sin(θjo)⋅sin(ϕjo)zjo=zjo+vjo⋅cos(θjo)(16)F4F_4F4(飞行器间避碰):
F4={∑i=1NAdi3,如果 di3<ds0,否则(17) F_4 = \begin{cases} \sum_{i=1}^{NA} d_i^3, & \text{如果 } d_i^3 < d_s \\ 0, & \text{否则} \end{cases} \tag{17} F4={∑i=1NAdi3,0,如果 di3<ds否则(17)
其中di3d_i^3di3为第iii个飞行器到其他飞行器的距离和:
di3=∑j=1,j≠iNA(xic−xjc)2+(yic−yjc)2+(zic−zjc)2(18) d_i^3 = \sum_{j=1,j \neq i}^{NA} \sqrt{(x_i^c - x_j^c)^2 + (y_i^c - y_j^c)^2 + (z_i^c - z_j^c)^2} \tag{18} di3=j=1,j=i∑NA(xic−xjc)2+(yic−yjc)2+(zic−zjc)2(18)
3. 提出的SaUSDE算法
在基础差分进化(DE)算法中,全局与局部搜索能力存在不平衡。为克服这一限制,本文提出一种自适应更新策略差分进化(SaUSDE)算法。对于极值点较少的优化问题,应采用局部搜索能力更强的变异算子;而对于极值点较多的问题,则需选择全局搜索能力更强的变异算子。单一更新策略往往难以平衡全局与局部搜索能力,形成显著障碍。在SaUSDE中,我们引入了四种源自DE变体的更新策略,通过轮盘赌机制动态调用。初始时,各策略的选择概率均等,但在算法迭代过程中,通过自主学习,表现更优的策略将获得更高的调用频率。此外,本文还设计了一种新的局部搜索算子以增强局部搜索能力,从而克服原始DE算法中局部与全局搜索能力不平衡的问题,适用于各类优化问题。
3.1. 交叉操作
在原始DE中,交叉概率(CRCRCR)为固定值,通常取值范围为[0,1][0,1][0,1]。当CRCRCR接近0时,个体在连续代际间的变化极小,导致种群中个体高度相似,可能陷入局部最优;而当CRCRCR接近1时,更新后的个体位置波动剧烈,阻碍算法收敛。CRCRCR在算法初期不应保持较大值,后期则需确保变异概率。文献表明,CRCRCR作为差分进化算法的关键参数,通过调控试验个体基因的概率性继承,直接影响种群多样性和收敛效率。算法初期,种群来源差异大,多样性较高,此时CRCRCR需保持较低值以避免因过度多样性导致的收敛缓慢;随着迭代进行,种群向量逐渐收敛,差异减小,此时CRCRCR应逐步增大以增强多样性并加速收敛。基于此,本文采用动态线性递增的交叉概率策略:
CR=CRmin+(CRmax−CRmin)⋅(nFEsmax_nFEs)(19) CR = CR_{\text{min}} + (CR_{\text{max}} - CR_{\text{min}}) \cdot \left(\frac{nFEs}{max\_nFEs}\right) \tag{19} CR=CRmin+(CRmax−CRmin)⋅(max_nFEsnFEs)(19)
其中CRmax=0.69CR_{\text{max}}=0.69CRmax=0.69,CRmin=0.45CR_{\text{min}}=0.45CRmin=0.45,nFEsnFEsnFEs为当前函数评估次数,max_nFEsmax\_nFEsmax_nFEs为最大函数评估次数。如公式(19)所示,初期目标向量与变异向量的数量几乎相等。CRmaxCR_{\text{max}}CRmax设置为0.99,确保即使在进化后期仍能保持足够的种群多样性,从而在优化过程中平衡探索与开发。
3.2 源自DE变体的更新策略
第一种策略
第一种DE更新策略源自文献[50],部分灵感来自灰狼优化器(GWO)[51]的改进,如公式(20)所示:
xnewi,j={xi,j+F⋅(xbest,j−xi,j+xR1,j−xR2,j),如果 rand<CR13(xbest,j+xsec,j+xthi,j),否则(20) xnew_{i,j} = \begin{cases} x_{i,j} + F \cdot (x_{best,j} - x_{i,j} + x_{R1,j} - x_{R2,j}), & \text{如果 } rand < CR \\ \frac{1}{3}(x_{best,j} + x_{sec,j} + x_{thi,j}), & \text{否则} \end{cases} \tag{20} xnewi,j={xi,j+F⋅(xbest,j−xi,j+xR1,j−xR2,j),31(xbest,j+xsec,j+xthi,j),如果 rand<CR否则(20)
其中:
- xbestx_{best}xbest、xsecx_{sec}xsec和xthix_{thi}xthi分别表示当前种群中适应度排名前三的个体
- FFF为缩放因子,取值范围[0.1,1.0][0.1,1.0][0.1,1.0]的随机数
- R1R1R1和R2R2R2是从种群中随机选择的两个不同于第iii个的个体
第二种策略
第二种DE更新策略源自文献[52],如公式(21)所示:
xnewi,j=xi,j+L⋅(xR1,j−xi,j)+F⋅(xR2,j−xR3,j)(21) xnew_{i,j} = x_{i,j} + L \cdot (x_{R1,j} - x_{i,j}) + F \cdot (x_{R2,j} - x_{R3,j}) \tag{21} xnewi,j=xi,j+L⋅(xR1,j−xi,j)+F⋅(xR2,j−xR3,j)(21)
其中:
- LLL为[0,1][0,1][0,1]范围内的随机数
- R1R1R1、R2R2R2和R3R3R3是从种群中随机选择的三个不同于第iii个的个体
第三种策略
第三种策略为"DE/best/1",如公式(22)所示:
xnewi,j=xbest,j+F⋅(xR1,j−xR2,j)(22) xnew_{i,j} = x_{best,j} + F \cdot (x_{R1,j} - x_{R2,j}) \tag{22} xnewi,j=xbest,j+F⋅(xR1,j−xR2,j)(22)
第四种策略
第四种策略为"DE/current to best/1",如公式(23)所示:
xnewi,j=xi,j+F⋅(xbest,j−xi,j)+F⋅(xR1,j−xR2,j)(23) xnew_{i,j} = x_{i,j} + F \cdot (x_{best,j} - x_{i,j}) + F \cdot (x_{R1,j} - x_{R2,j}) \tag{23} xnewi,j=xi,j+F⋅(xbest,j−xi,j)+F⋅(xR1,j−xR2,j)(23)
3.3. SaUSDE的实现
在本文提出的算法中,采用轮盘赌方法选择调用公式(20)-(23)。初始时,各策略被选中的概率相等。在后续迭代中,若某策略在第ttt次迭代中表现更优,则其积分增加1。积分更高的策略在后续迭代中被调用的概率更高,具体公式如下:
pj(t+1)=sj(t)∑i=1SNsi(t),j∈{1,2,…,SN}(24) p_j(t+1) = \frac{s_j(t)}{\sum_{i=1}^{SN} s_i(t)}, \quad j \in \{1,2,\dots,SN\} \tag{24} pj(t+1)=∑i=1SNsi(t)sj(t),j∈{1,2,…,SN}(24)
其中pj(t+1)p_j(t+1)pj(t+1)表示策略jjj在下次迭代中被调用的概率,sj(t)s_j(t)sj(t)为策略jjj在当前迭代的积分,SNSNSN为策略总数(本文设为4)。最优策略通过轮盘赌方法确定。SaUSDE算法的伪代码和流程图分别如算法1和图1所示。
4.3.求解球形多飞行器路径规划问题的SaUSDE
SaUSDE应用于球形多飞行器路径规划问题。整体模型包括四个组件,如图3所示。第一个组件是半径为R的大球体,其中飞行器只能在表面飞行,不能进入球体内部。第二个组件由飞行器组成,本文表示为均匀的灰色球体。每架飞行器都有自己的起点(○)和终点(×),飞行路径完全随机生成。第三个组件是禁飞区,配置为禁止飞行器进入的多个红色半球区域。第四部分由未知飞行物组成,每个飞行物都表示为一个蓝色球体,其飞行轨迹被描绘为虚线蓝线。每个未知飞行物都严格遵循其飞行轨迹,飞机遇到它们时必须绕行它们。
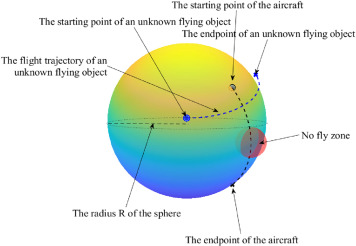
图3.球形多飞行器路径规划问题的基本布局。
以下是表格中的信息翻译成中文:
| 场景 | 飞机数量 | 禁飞区数量 | 未知飞行物数量 |
|---|---|---|---|
| 场景 1 | 3 | 2 | 1 |
| 场景 2 | 5 | 3 | 2 |
| 场景 3 | 8 | 2 | 2 |
| 场景 4 | 12 | 5 | 6 |
4.3.1模拟实验的布局设置
为了验证基于SaUSDE在球形飞行器系统中的性能的飞行器总数的影响,本实验创建了四种不同飞行器数量的情景,图4、图5、图6、图7分别呈现了这些模拟情景,在这些情景中,飞行器、禁飞区和未知飞行物体的数量在表8中提供。
表8 不同场景下飞行器数量、禁飞区数量、未知飞行物数量
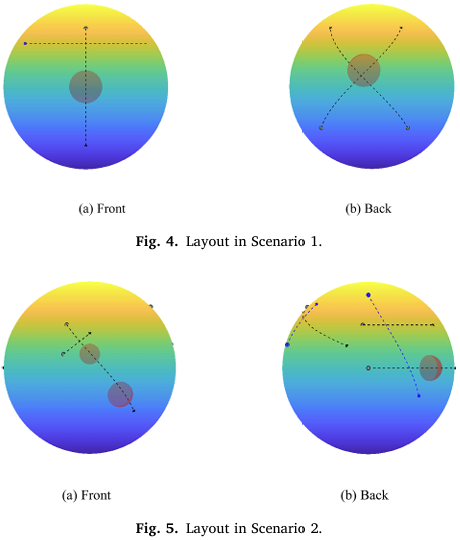
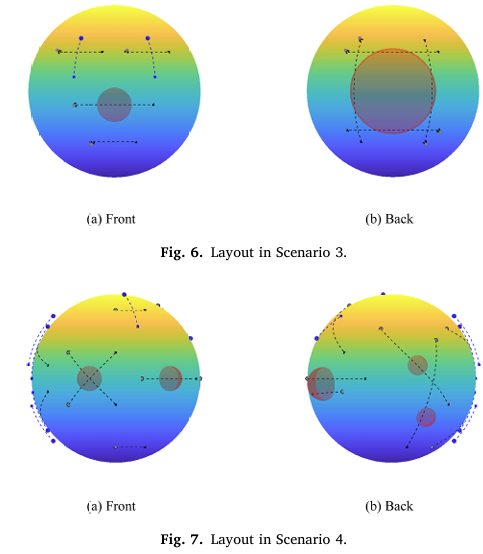
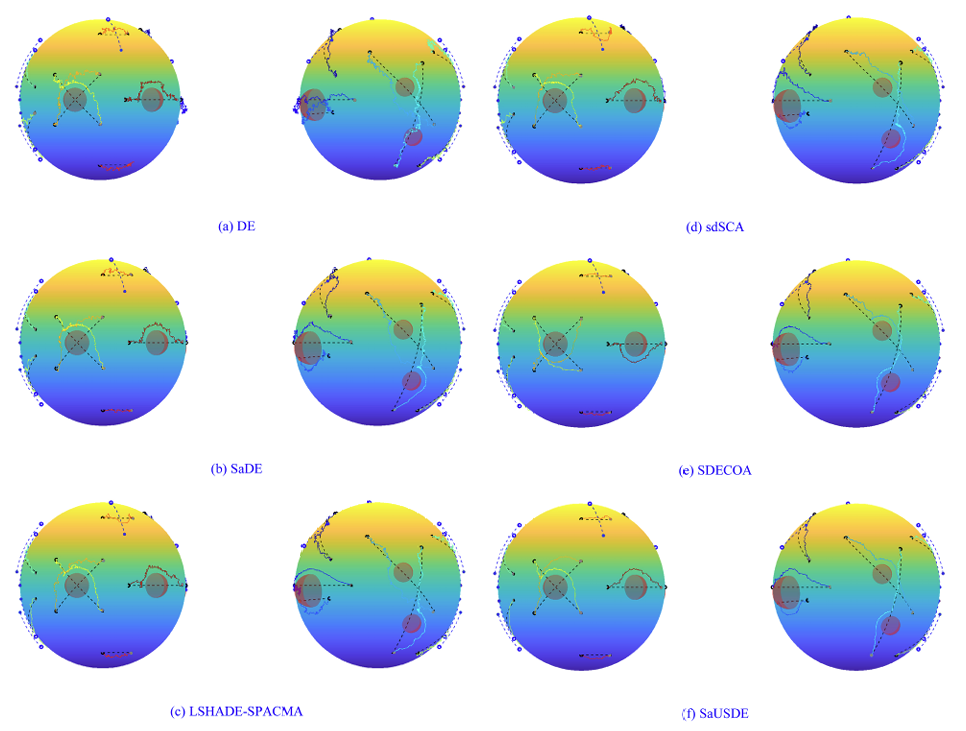
4.3.2 情景4中模拟实验的分析
Zhu L, Zhou Y Q, Zhou G, Luo Q F, Wei Y F. Solving spherical multi-aircraft path planning problem using self-adaptive update strategy differential evolution algorithm[J]. Swarm and Evolutionary Computation, 2025, 96: 102004.https://doi.org/10.1016/j.swevo.2025.102004