1. 快排性能的关键点分析
决定快排性能的关键点是每次单趟排序后,key对数组的分割,如果每次选key基本二分居中,那么快排的递归树就是颗均匀的满二叉树,性能最佳。
但是实践中虽然不可能每次都是二分居中,但是性能也还是可控的。但是如果出现每次选到最小值 / 最大值,划分为0个和N-1的子问题时,时间复杂度为O(N^2),数组序列有序时就会出现这样的问题,我们前面已经用三数取中选key、随机选key解决了这个问题,也就是说我们解决了绝大多数的问题,但是现在还是有一些场景没解决(数组中有大量重复数据时),类似以下代码。
// 数组中有多个跟key相等的值
int a[] = { 6,1,7,6,6,6,4,9 };
int a[] = { 3,2,3,3,3,3,2,3 };
// 数组中全是相同的值
int a[] = { 2,2,2,2,2,2,2,2 };1.1 hoare版本(左右指针)、lomuto版本(前后指针)
以下是《算法导论》书籍中给出的hoare和lomuto给出的快排的单趟排序的伪代码:

代码分析。
hoare版本
- 把最左侧元素 A[p] 当作“枢轴” pivot(记为 x)。
- i 从 p 的左边一格开始。
- j 从 r 的右边一格开始。
- 无限循环:
不断把 j 往左移,直到 A[j] ≤ pivot(找到右侧一段中 ≤ pivot 的元素)。
不断把 i 往右移,直到 A[i] ≥ pivot(找到左侧一段中 ≥ pivot 的元素)。
如果这时 i 还在 j 的左边,说明 A[i] 与 A[j] 位置反了,交换它们,然后继续 while TRUE 循环。
一旦 i ≥ j,说明左右指针已经交错,整个区间划分完成,返回 j(最后一个小于等于 pivot 的元素下标)。lomuto版本
- 把最右侧元素 A[r] 当作 pivot。
- i 也从 p 的左边一格开始,用来标记“已处理区间内最后一个 < pivot 的位置”。
- 用 j 从左到右扫描 [p, r-1]。
- 如果 A[j] 比 pivot 小,就把 i 右移一格(扩大“小元素区间”),然后把 A[j] 交换到该区间的末尾。
- 循环结束后,i+1 就是 pivot 应该待的位置,再和 A[r] 交换。
- 返回 i+1,调用者即可知道 pivot 最终下标。
一句话总结
Hoare:双向夹击,交换次数少,返回的是“分界”下标 j,但 pivot 本身不一定在 j 上。
Lomuto:单向扫描,代码更短,返回的是 pivot 实际落位 i+1,但交换次数略多。
| 特性 | Hoare 划分 | Lomuto 划分 |
|---|---|---|
| 枢轴选择 | 最左元素 A[p] |
最右元素 A[r] |
| 划分方式 | 双向扫描,从两端向中间逼近 | 单向扫描,从左到右 |
| 返回值 | 返回 j,即最后一个小于等于枢轴的元素索引 |
返回 i+1,即枢轴最终位置 |
| 交换次数 | 较少,通常更高效 | 较多,可能效率略低 |
| 稳定性 | 不稳定 | 不稳定 |
| 边界条件 | 更复杂,需处理 i < j |
简单直观 |
两个关键问题
初始时
i = p – 1会不会越界?第一次
i = i + 1后指向A[p],会不会立刻把枢轴A[p]换走?
1. 关于“越界”
2. 关于“第一次就停在 A[p] 并把它换掉”
i的初始值确实是p – 1,但它并没有立即去访问A[p – 1]。在 Hoare 的代码里,
i第一次被使用是在第 9 行的repeat … until循环里,而第 9 行先执行i = i + 1再访问A[i]。也就是说,真正第一次访问
A[i]时i已经变成p,不会踩到p – 1。因此不存在数组越界的实际读写。
在 Hoare 的算法里,枢轴选的是
A[p],但 Hoare 并不保证枢轴最后一定待在p位置——它在划分过程中完全可能被交换到别的位置。第一次
i自增后确实指向A[p],但此时不会立刻发生交换,因为还要再看j那边的扫描结果:
– 只有当A[i] ≥ x且A[j] ≤ x时才会交换。
– 如果A[p]恰好就是最小值,那么A[i]在第一次比较时就满足A[i] ≥ x,而另一侧的j会停在某个 ≤ x 的位置,于是A[p]会被换走——这正是算法想要的:把“过大”的元素移到右边,把“过小”的元素移到左边。所以“把
A[p]换走”不是 bug,而是设计如此;Hoare 划分结束后,枢轴不一定留在返回的索引上,但区间已被正确划分成“左侧 ≤ pivot,右侧 ≥ pivot”。
一句话总结
i从p – 1开始只是为了延迟一位再访问,第一次真正用到时已经变成p,不会越界;而A[p]被交换走是算法允许的,因为 Hoare 并不保留枢轴在原始位置。
示例对比
假设数组
A = [5, 3, 8, 4, 2],初始p = 0, r = 4:
Lomuto(枢轴
A[r] = 2):
最终数组:
[2, 3, 8, 4, 5],返回0(枢轴 2 的位置)。Hoare(枢轴
A[p] = 5):
最终数组:
[2, 3, 4, 8, 5],返回2(最后一个小于等于 5 的元素索引,即 5 自身)。
✅ Hoare 划分
优点:
通常比 Lomuto 更快,交换次数更少。
在数组两端向中间扫描,适合大数据量。
缺点:
代码逻辑稍复杂,边界条件容易出错。
返回的索引
j并不一定是枢轴的最终位置(需结合快速排序主算法理解)。✅ Lomuto 划分
优点:
代码简洁,易于理解和实现。
返回值直接是枢轴的最终位置,方便快速排序主算法使用。
缺点:
交换次数较多,性能略逊于 Hoare。
当数组中有大量重复元素时,效率下降明显。
1.2 hoare和lomuto单趟排序代码分析
数组中有大量重复数据时,快排单趟选key划分效果对象:
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
printf("%d ", a[i]);
printf("\n");
}
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
// hoare
// [left, right]
int PartSort1(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
// 右边找⼩
while (left < right && a[right] >= a[keyi])
--right;
// 左边找⼤
while (left < right && a[left] <= a[keyi])
++left;
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;
}
// 前后指针
int PartSort2(int* a, int left, int right)
{
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
typedef struct
{
int leftKeyi;
int rightKeyi;
}KeyWayIndex;
// 三路划分
KeyWayIndex PartSort3Way(int* a, int left, int right)
{
int key = a[left];
// left和right指向就是跟key相等的区间
// [开始, left-1][left, right][right+1, 结束]
int cur = left + 1;
while (cur <= right)
{
// 1、cur遇到⽐key⼩,⼩的换到左边,同时把key换到中间位置
// 2、cur遇到⽐key⼤,⼤的换到右边
if (a[cur] < key)
{
Swap(&a[cur], &a[left]);
++cur;
++left;
}
else if (a[cur] > key)
{
Swap(&a[cur], &a[right]);
--right;
}
else
{
++cur;
}
}
KeyWayIndex kwi;
kwi.leftKeyi = left;
kwi.rightKeyi = right;
return kwi;
}
void TestPartSort1()
{
int a1[] = { 6,1,7,6,6,6,4,9 };
int a2[] = { 3,2,3,3,3,3,2,3 };
int a3[] = { 2,2,2,2,2,2,2,2 };
PrintArray(a1, sizeof(a1) / sizeof(int));
int keyi1 = PartSort1(a1, 0, sizeof(a1) / sizeof(int) - 1);
PrintArray(a1, sizeof(a1) / sizeof(int));
printf("hoare keyi:%d\n\n", keyi1);
PrintArray(a2, sizeof(a2) / sizeof(int));
int keyi2 = PartSort1(a2, 0, sizeof(a2) / sizeof(int) - 1);
PrintArray(a2, sizeof(a2) / sizeof(int));
printf("hoare keyi:%d\n\n", keyi2);
PrintArray(a3, sizeof(a3) / sizeof(int));
int keyi3 = PartSort1(a3, 0, sizeof(a3) / sizeof(int) - 1);
PrintArray(a3, sizeof(a3) / sizeof(int));
printf("hoare keyi:%d\n\n", keyi3);
}
void TestPartSort2()
{
int a1[] = { 6,1,7,6,6,6,4,9 };
int a2[] = { 3,2,3,3,3,3,2,3 };
int a3[] = { 2,2,2,2,2,2,2,2 };
PrintArray(a1, sizeof(a1) / sizeof(int));
int keyi1 = PartSort2(a1, 0, sizeof(a1) / sizeof(int) - 1);
PrintArray(a1, sizeof(a1) / sizeof(int));
printf("前后指针 keyi:%d\n\n", keyi1);
PrintArray(a2, sizeof(a2) / sizeof(int));
int keyi2 = PartSort2(a2, 0, sizeof(a2) / sizeof(int) - 1);
PrintArray(a2, sizeof(a2) / sizeof(int));
printf("前后指针 keyi:%d\n\n", keyi2);
PrintArray(a3, sizeof(a3) / sizeof(int));
int keyi3 = PartSort2(a3, 0, sizeof(a3) / sizeof(int) - 1);
PrintArray(a3, sizeof(a3) / sizeof(int));
printf("前后指针 keyi:%d\n\n", keyi3);
}
void TestPartSort3()
{
//int a0[] = { 6,1,2,7,9,3,4,5,10,4 };
int a1[] = { 6,1,7,6,6,6,4,9 };
int a2[] = { 3,2,3,3,3,3,2,3 };
int a3[] = { 2,2,2,2,2,2,2,2 };
PrintArray(a1, sizeof(a1) / sizeof(int));
KeyWayIndex kwi1 = PartSort3Way(a1, 0, sizeof(a1) / sizeof(int) - 1);
PrintArray(a1, sizeof(a1) / sizeof(int));
printf("3Way keyi:%d,%d\n\n", kwi1.leftKeyi, kwi1.rightKeyi);
PrintArray(a2, sizeof(a2) / sizeof(int));
KeyWayIndex kwi2 = PartSort3Way(a2, 0, sizeof(a2) / sizeof(int) - 1);
PrintArray(a2, sizeof(a2) / sizeof(int));
printf("3Way keyi:%d,%d\n\n", kwi2.leftKeyi, kwi2.rightKeyi);
PrintArray(a3, sizeof(a3) / sizeof(int));
KeyWayIndex kwi3 = PartSort3Way(a3, 0, sizeof(a3) / sizeof(int) - 1);
PrintArray(a3, sizeof(a3) / sizeof(int));
printf("3Way keyi:%d,%d\n\n", kwi3.leftKeyi, kwi3.rightKeyi);
}
int main()
{
TestPartSort1();
TestPartSort2();
TestPartSort3();
return 0;
}1.3 三路划分算法解析
快排确实快,但是由于“选key,划分区间,递归”这样的思路,导致围绕选key出现一些极端场景导致快排的效率退化到O(N^2)
之前的代码思想:
- 比key小的在左边,比key大的在右边;
- 相等的不管,原来在左/右边就继续在左/右边;
- 一次快排,排好1个key值数据的位置。
当面对有大量跟key相同的值时,三路划分的核心思想是把数组中的数据分为三段:
【比key小的值】 【跟key相等的值】【比key大的值】
所以叫做三路划分算法。
- key值有m个重复的数据,则一次三路划分,排好m个数据的位置。
单趟三路划分快排实现思想:
- 初始:key默认取left位置的值。
这里就不保存下标keyi了,直接保存key值,
因为keyi下标处的值在三路划分过程中会交换走。- 初始:left指向区间最左边,right指向区间最后边,cur指向left+1位置。
- cur遇到比key小的值后跟left位置交换,换到左边,left++,cur++。
(换过来的值肯定是key,所以cur可以往后走)
过程中left一直指向最左端的key值。- cur遇到比key大的值后跟right位置交换,换到右边,right--。
(换过来的值不确定,所以cur不能往后走)
交换完只有right往左走,然后看交换给cur的原right值是不是还比key大,还大还交换
小于key走第3步,等于key走第5步。- cur遇到跟key相等的值后,cur++。
- 直到cur > right结束。
cur = right还要继续。
图解分析。
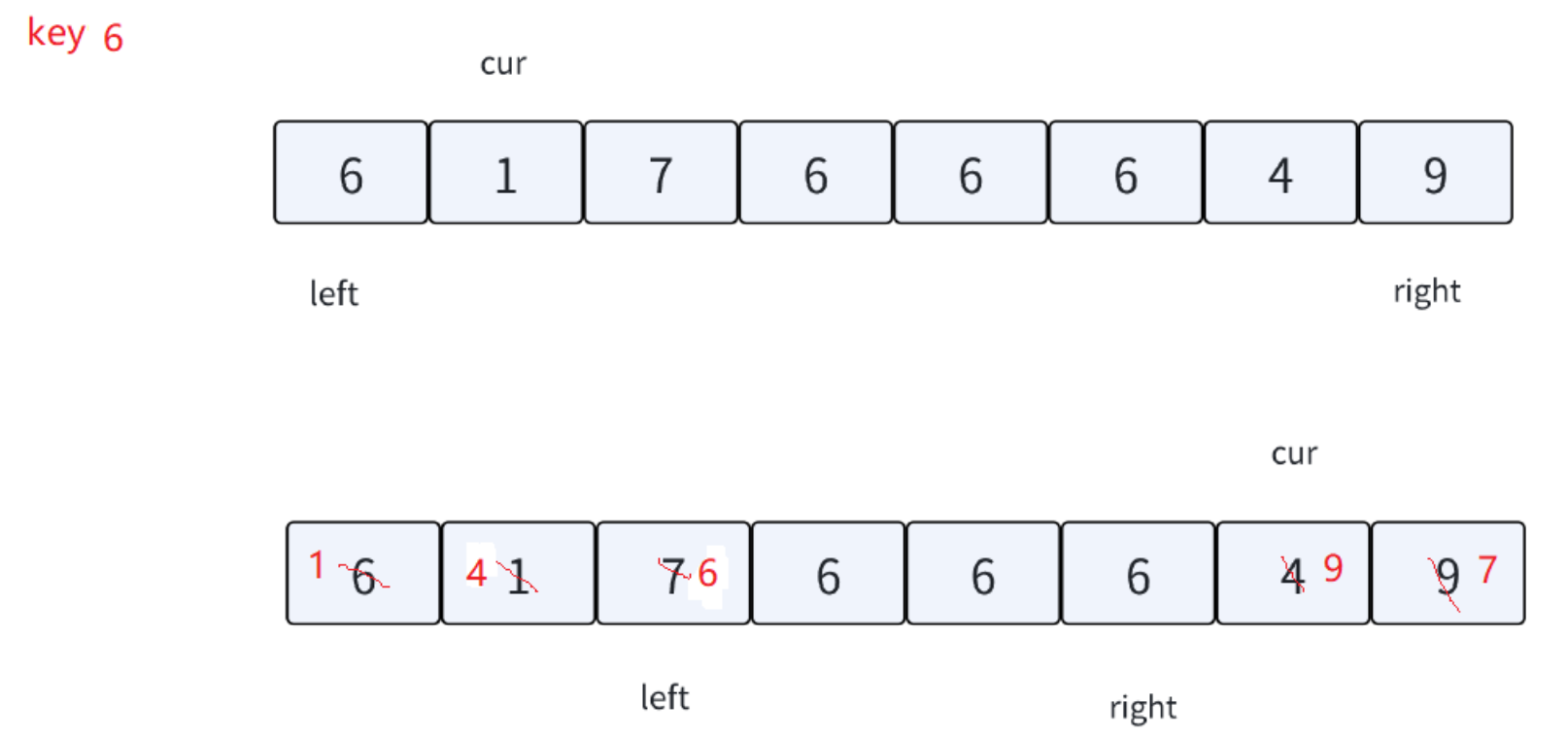
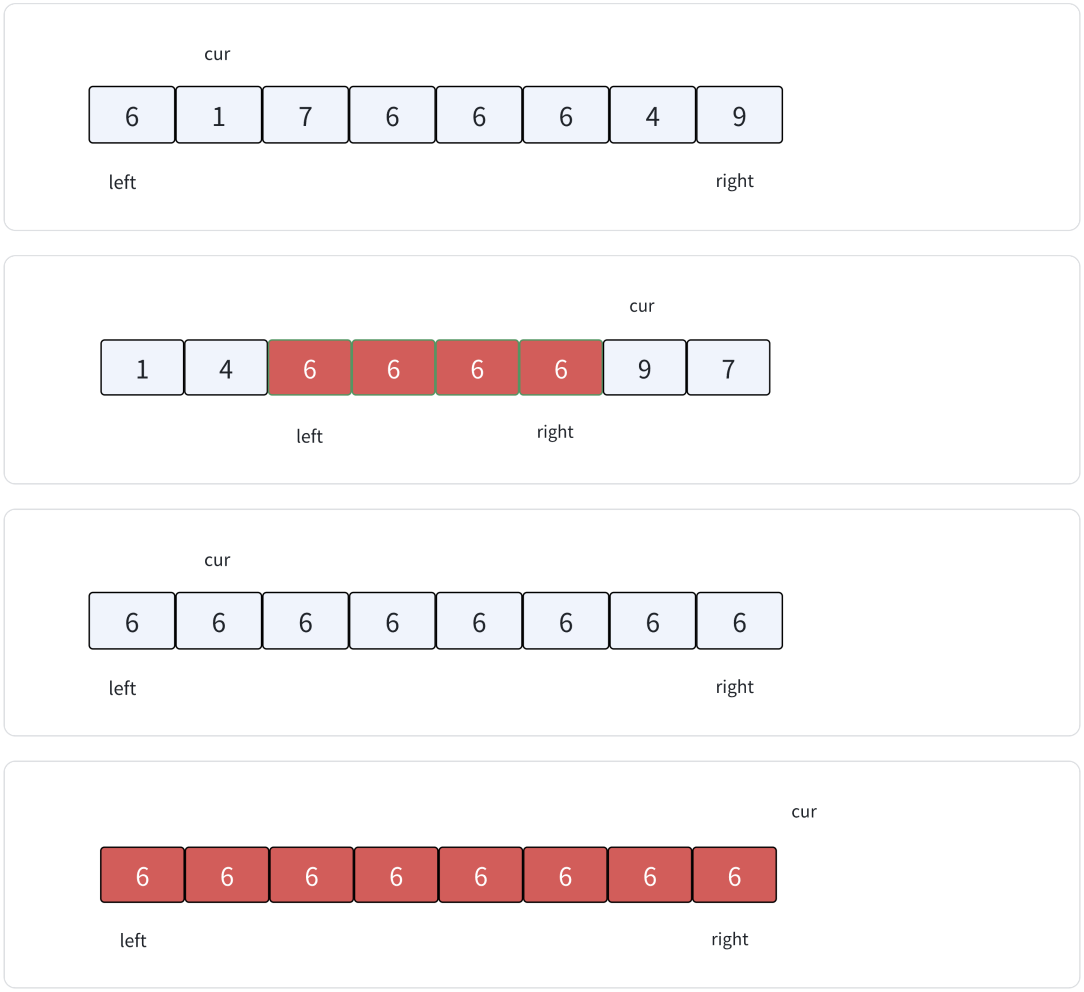
- 三个指针:left、right、cur(抽象意义上的指针,实际上是下标)
- 一次三路划分结束后:left、right指向key值区间的左、右下标。(左闭右闭的区间)
- 递归的左区间[begin,left-1]、右区间[right+1,end]。
三路划分的执行过程有点类似hoare的左右指针和lomuto的前后指针的结合。
三路划分结束:再递归左区间、右区间。
像这样全数据相同的数组,三路划分一次就没有左区间、右区间了,就不用继续排序了,排序结束。——三路划分专治这种有大量重复数据的数组。
// 三路划分
KeyWayIndex PartSort3Way(int* a, int left, int right)
{
int key = a[left];
// left和right指向就是跟key相等的区间
// [开始, left-1][left, right][right+1, 结束]
int cur = left + 1;
while (cur <= right)
{
// 1、cur遇到⽐key⼩,⼩的换到左边,同时把key换到中间位置
// 2、cur遇到⽐key⼤,⼤的换到右边
if (a[cur] < key)
{
Swap(&a[cur], &a[left]);
++cur;
++left;
}
else if (a[cur] > key)
{
Swap(&a[cur], &a[right]);
--right;
}
else
{
++cur;
}
}
KeyWayIndex kwi;
kwi.leftKeyi = left;
kwi.rightKeyi = right;
return kwi;
}三种快排单趟排序运行结果分析:
从下面的运行结果分析,无论是hoare,还是lomuto的前后指针法,面对key有大量重复时,划分都不是很理想。三数取中和随机选key,都不能很好的解决这里的问题。
但是三路划分算法,把跟key相等的值都划分到了中间,可以很好的解决这里的问题。
运⾏结果:6 1 7 6 6 6 4 94 1 6 6 6 6 7 9hoare keyi:23 2 3 3 3 3 2 32 2 3 3 3 3 3 3hoare keyi:62 2 2 2 2 2 2 22 2 2 2 2 2 2 2hoare keyi:06 1 7 6 6 6 4 94 1 6 6 6 6 7 9前后指针 keyi:23 2 3 3 3 3 2 32 2 3 3 3 3 3 3前后指针 keyi:22 2 2 2 2 2 2 22 2 2 2 2 2 2 2前后指针 keyi:06 1 7 6 6 6 4 91 4 6 6 6 6 9 73Way keyi:2,53 2 3 3 3 3 2 32 2 3 3 3 3 3 33Way keyi:2,72 2 2 2 2 2 2 22 2 2 2 2 2 2 23Way keyi:0,7
2. 排序OJ
力扣的OJ的通过标准是很严格的:①测试用例全;②对性能有要求。
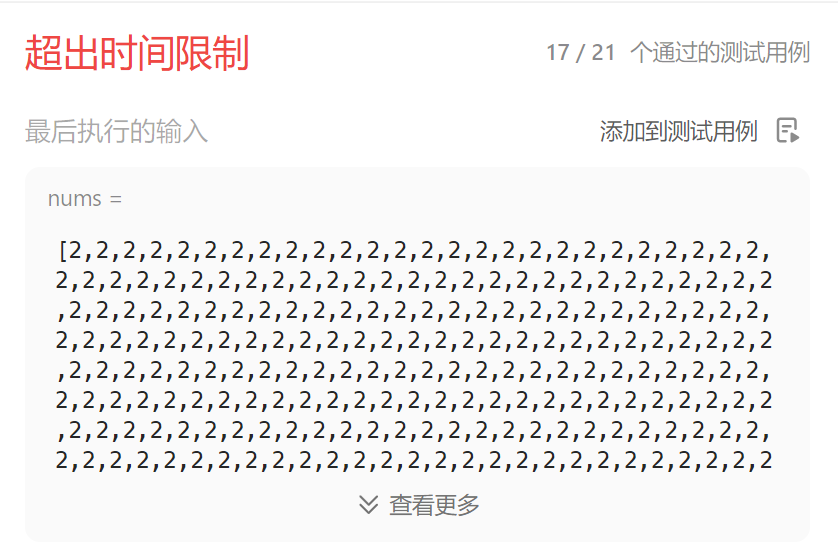
这道题官方给出的使用快速排序的解(lomuto、随机选key),都通不过——超出时间限制。
应该是早年的题解,后来测试人员新增了测试用例,导致通不过。
下面我们再来看看这个OJ题,这个OJ,当我们用快排的时候,传统的hoare和lomuto的方法,过不了这个题目。堆排序和归并和希尔是可以过的,其他几个O(N^2)也不过了,因为这个题的测试用例中不仅仅有数据很多的大数组,也有一些特殊数据的数组,如大量重复数据的数组。
堆排序和归并和希尔不是很受数据样本的分布和形态的影响,但是快排会,因为快排要选key,每次key都当趟分割都很偏,就会出现效率退化问题。
这里的快排的解决方案我们讲两种:
1. 上面讲的三路划分。
2. C++ STL sort中用的introspective sort(内省排序)。
(introsort是由David Musser在1997年设计的排序算法)
2.1 lomuto的快排跑排序OJ代码
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
// 随机选key
int randi = left + (rand() % (right-left+1));
// printf("%d\n", randi);
Swap(&a[left], &a[randi]);
int prev = left;
int cur = prev + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi+1, end);
}
int* sortArray(int* nums, int numsSize, int* returnSize){
srand(time(0));
QuickSort(nums, 0, numsSize-1);
*returnSize = numsSize;
return nums;
}运行结果:
2.2 快排·三路划分—跑排序OJ代码
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
// 随机选key
int randi = left + (rand() % (right-left));
Swap(&a[left], &a[randi]);
// 三路划分
// left和right指向就是跟key相等的区间
// [begin, left-1] [left, right] right+1, end]
int key = a[left];
int cur = left+1;
while(cur <= right)
{
// 1、cur遇到⽐key⼩,⼩的换到左边,同时把key换到中间位置
// 2、cur遇到⽐key⼤,⼤的换到右边
if(a[cur] < key)
{
Swap(&a[cur], &a[left]);
++left;
++cur;
}
else if(a[cur] > key)
{
Swap(&a[cur], &a[right]);
--right;
}
else
{
++cur;
}
}
// [begin, left-1] [left, right] right+1, end]
QuickSort(a, begin, left - 1);
QuickSort(a, right+1, end);
}
int* sortArray(int* nums, int numsSize, int* returnSize){
srand(time(0));
QuickSort(nums, 0, numsSize-1);
*returnSize = numsSize;
return nums;
}2.3 快排·内省排序—跑排序OJ代码
三路划分的快排的分析
- 针对有大量重复数据的数组而设计的,在排序随机数组时,相较于hoare、lomuto这样的普通快排算法,效率稍微没那么好——例如:cur遇到比key大,而right比key小,那cur和right交换,cur再和left交换,多了一个中间商作交换。或者right本身就比key大,交换给cur后,cur还要再交换回来给right。
- 针对随机数组,还是有可能选到最小/大值作key,导致性能退化。
introsort是introspective sort采用了缩写,它的名字其实表达了它的实现思路。
introsort的快排的思路就是进行自我侦测和反省:
- 快排递归深度太深(sgi stl中使用的是深度为2倍排序元素数量的对数值),那就说明在这种数据序列下,选key出现了问题,性能在快速退化。
- 递归到一定深度(2*logN-留出冗余),不再使用快排继续递归,改换为堆排序。
归并排序有O(N)的时间复杂度
考虑各种因素下,2*logN比较合适。
- 记录递归深度——用一个函数参数来做这件事。
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 选出左右孩子中大的那⼀个
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序——快排的内省优化
void HeapSort(int* a, int n)
{
// 建堆 -- 向下调整建堆 -- O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
// 自己先实现 -- O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
--end;
}
}
//插入排序——快排的小区间优化
void InsertSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
int end = i-1;
int tmp = a[i];
// 将tmp插⼊到[0,end]区间中,保持有序
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
//内省排序
void IntroSort(int* a, int left, int right, int depth, int defaultDepth)
{
if (left >= right)
return;
// 数组长度⼩于16的⼩数组,换为插⼊排序,简单递归次数
if(right - left + 1 < 16)
{
InsertSort(a+left, right-left+1);
return;
}
// 当深度超过2*logN时改⽤堆排序
if(depth > defaultDepth)
{
HeapSort(a+left, right-left+1);
return;
}
depth++;
int begin = left;
int end = right;
// 随机选key
int randi = left + (rand() % (right-left));
Swap(&a[left], &a[randi]);
int prev = left;
int cur = prev + 1;
int keyi = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
// [begin, keyi-1] keyi [keyi+1, end]
IntroSort(a, begin, keyi - 1, depth, defaultDepth);
IntroSort(a, keyi+1, end, depth, defaultDepth);
}
//快速排序
void QuickSort(int* a, int left, int right)
{
int depth = 0;
int logn = 0;
int N = right-left+1;
//计算logN——库里面有log函数,底层也是这样实现的(省去函数调用的消耗——函数栈帧的建立和销毁)
for(int i = 1; i < N; i *= 2)
{
logn++;
}
// introspective sort -- 自省排序
IntroSort(a, left, right, depth, logn*2);
}
int* sortArray(int* nums, int numsSize, int* returnSize){
srand(time(0));
QuickSort(nums, 0, numsSize-1);
*returnSize = numsSize;
return nums;
}