运动场和光流-动手学计算机视觉17

介绍

在一个不断运动的世界中，我们的眼睛和大脑能够自然而然地感知到周围环境的运动。与此对应，计算机视觉技术面临的一个挑战是如何从获取的图像序列中提取出运动信息。通过运动场(motion field)和光流(optical flow)估计，我们可以从视频中重建运动信息。运动场描述了三维世界中点的运动在二维成像平面上的投影，如图17-1所示。

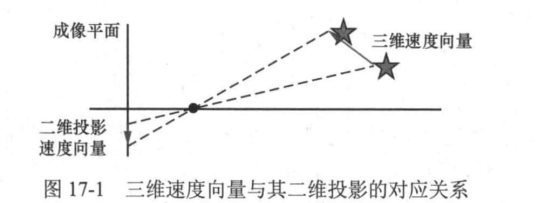
运动场是图像上所有像素对应的三维空间点的三维速度向量在成像平面上的二维投影速度向量所形成的场。运动场是三维运动在二维成像平面上的理想表示，它直接关联到物体的实际物理运动，但我们无法直接从图像中观测到这种运动，只能通过分析图像序列中的光流来近似估计运动场。

光流定义为图像序列中由物体、照相机或光照变化引起的像素亮度随时间变化的表现。它由图像强度的变化计算而来，被视为像素二维投影速度向量的一个近似。整个图像平面上所有像素的光流向量构成了光流场，描述了图像层面的运动模式，是二维运动场的一个近似。然而光流场并不总是与实际的运动场一致，因为光流可能受到光照变化等非运动因素的影响。

美国心理学家James J.Gibson在20世纪40年代首次提出了光流的概念四，自那以后，光流估计就成为计算机视觉领域的研究热点，并在运动分析、目标跟踪、图像配准和三维重建等多个方面得到了广泛应用。本章将深入介绍光流估计的基本原理和经典方法，通过理解和应用这些方法，我们可以更好地从视频中重建运动信息，使从二维图像中构建出的物体运动更接近于真实的三维物理世界的目标的运动。

运动场投影

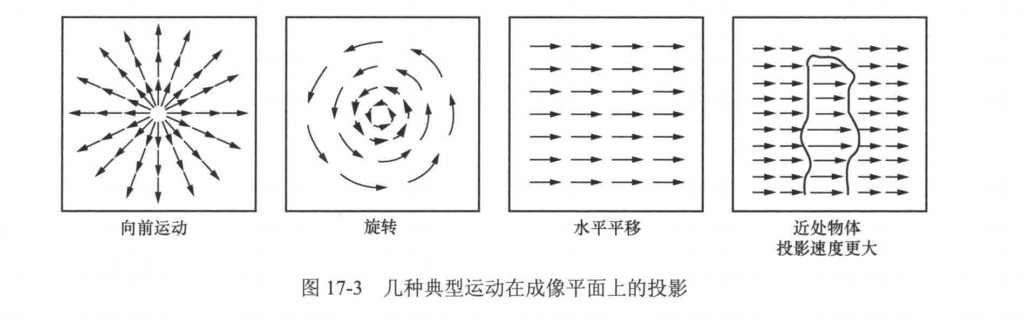
光流

在多数情况下，直接计算物体的运动场并不可行，我们通常采用计算光流的方法来近似估计物体的运动场。接下来我们将探讨光流估计的基本原理和常用的计算方法。

特征点法

光流本质上是由图像亮度变化产生的二维像素变化，因此可以通过跟踪图像中的特征点来计算。如第7章所述，从图像中提取视觉特征（如角点和块状区域），并在连续帧之间追踪这些特征点的对应关系，是计算光流的一种方法。这种基于特征点的光流估计产生的是稀疏光流，尽管它在表达多帧之间的运动关系上很鲁棒，尤其适用于描述较大位移的相对运动，但也存在以下局限性。

(1)计算成本高：特征点的提取和描述符的计算过程非常耗时。例如，SIFT算法在CPU上运行并不能实现实时计算，而ORB算法也需要大约20s的计算时间。

(2)信息利用不充分：采用特征点方法时，图像中除了特征点之外的所有信息都被忽略了。一幅图像可能包含数十万像素点，而特征点的数量通常只有几百个，这意味着大量可能有用的图像信息被丢弃。

(3)特征匮乏的场景：照相机有时可能移动到缺乏明显特征的场景中，例如面对一堵白墙或者空旷的走廊，这些场景中特征点的数量可能大幅减少，难以找到足够的匹配点来准确计算光流和照相机的运动。

直接法

利用图像的像素亮度信息来估计运动，不需要计算特征点和描述子，这使其能够在特征缺失的情况下有效进行运动估计。只要场景中存在亮度变化（无论是渐变还是不足以形成局部图像梯度的变化)，直接法都能够发挥作用。与仅能重建稀疏光流的特征点法不同，直接法能够根据可用像素的数量构建稀疏、稠密或半稠密的光流。然而，直接法对图像外观的变化(如亮度变化)较为敏感，可能会错误地将这些变化解释为运动。因此，这类方法更适用于在视频中运动幅度较小的情况下计算光流。

接下来，我们介绍如何使用直接法计算光流。如图17-4所示

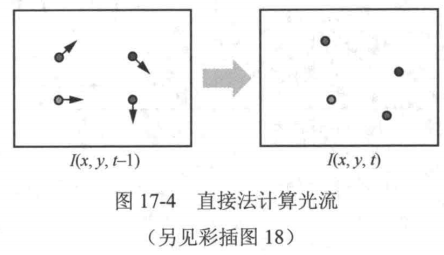
给定运动前后的两帧I(x,y,t-1)和I(x,y,t),我们的目标是找到图像中像素之间的对应关系，从而得到每个像素的光流。为了直接从像素层面找到像素间的对应关系，需要引入以下假设。

(1)亮度恒定：假设三维世界中一点在二维图像中对应的像素的亮度不随时间变化。这意味着具有这种对应关系的像素的亮度值在连续帧中不会发生变化。

(2)微小移动：假设在短时间内，三维点的移动是微小的。根据亮度恒定假设，即一个三维点在二维图像中对应的像素在时间t一1和时间t的亮度值保持不变

我们可以推出图像亮度的空间梯度和时间梯度之间的关系的方程

这个方程表达了图像亮度的空间梯度和时间梯度之间的关系，可用于估计像素亮度随时间的运动，即光流，因此也被称为光流方程。然而，这个方程中存在两个未知数u和v,仅由这一个方程无法得到未知数的确定解，需要通过额外的约束或优化方法来求解

Lucas-Kanade光流法

为了解决上述方程中的欠定问题，Lucas-Kanade光流法引入了空间一致性假设，即假定场景中相同表面的相邻点具有相似的运动，这些点投影到成像平面上时也保持邻近，并且它们的运动速度也相似。这意味着，如果我们考虑一个特征点及其邻域内的点，我们可以假设这些点在x轴和y轴方向上的速度是相同的。以图17-5为例

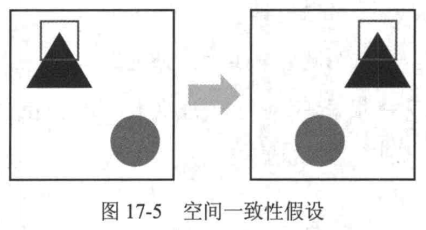
在一个邻域内，如方框标注的区域内，所有光流向量可以认为是一致的。因此，通过在这样的特征区域内应用光流方程，我们可以联立多个方程来求解该区域内的统一速度u和v。具体而言，假定使用一个5×5的窗口作为空间图17-5空间一致性假设一致性假设区域，那么在这个窗口中的每个像素都可以计算一次光流方程，总共能够得到25个方程，肯定可以求解统一速度u,v

而且因为和角点检测算法Harris类似，所以Lucas-Kanade光流法在角点处效果最好

Lucas-Kanade光流法的改进

Lucas-Kanade光流法的约束条件就是它的三大假设：亮度恒定、微小移动和空间一致性。

虽然在许多情况下这些假设是有效的，但它们也带来了一些限制，尤其是在处理快速运动的物体或亮度变化显著的场景时。

为了提高算法的泛用性和鲁棒性，研究人员和工程人员后续又做了诸多工作。这里我们简单介绍一些实用的改进方法。

(1)迭代法

通过逐步估计光流然后更新光流的形式来计算光流。如图17-6所示

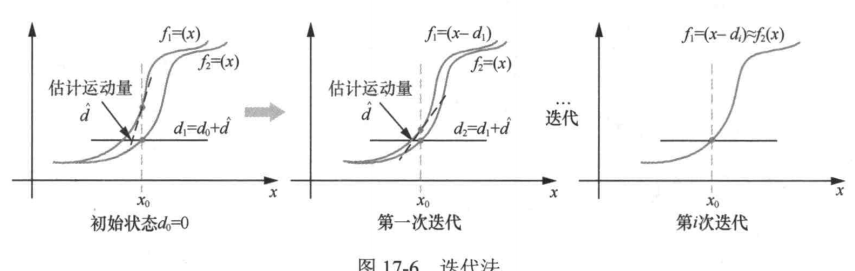
迭代法初始阶段从位移估计开始，通过使用Lucas-Kanade光流法得到一个初步估计的速度向量a,并更新向量接着，将第一帧图像根据当前的位移结果进行扭曲，使其更接近第二帧图像的亮度分布。通过不断迭代这个过程，计算新的估计值并累加每次迭代得到的速度向量，最终得到精确的光流估计，使得扭曲后的第一帧亮度与第二帧亮度几乎一致。

(2)多尺度图像法（图像金字塔法）

针对两帧之间物体运动位移较大的情况，通过构建图像金字塔降低图像的尺寸，从而减小像素位移（如图17-7所示)

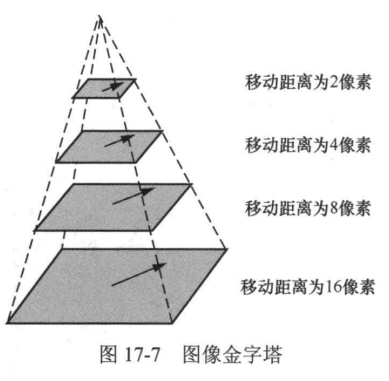
使微小移动假设再次成立。例如，原图像尺寸为400像素×400像素，此时像素在图像平面上的移动距离为16像素；当图像缩小为200像素×200像素时，移动距离就变成了8像素；进一步缩小为100像素×100像素时，移动距离变为4像素。

代码实现

接下来让我们动手学习 Lucas-Kanade 算法。首先，我们制造一张噪音图像并将其顺时针旋转1度。

import cv2
import numpy as np
import matplotlib.pyplot as plt
import random
import math

# 根据角度旋转图像
def rotate_image(img, angle):
    # 计算旋转中心
    center = tuple(np.array(img.shape[1::-1]) / 2)
    # 计算旋转矩阵
    rot_mat = cv2.getRotationMatrix2D(center, angle, 1.0)
    # 旋转图像
    rotated = cv2.warpAffine(img, rot_mat, 
                    img.shape[1::-1], flags=cv2.INTER_LINEAR)
    return rotated

# 创建一个200*200的随机数组，并将其转换为float32类型
img_t0 = np.random.rand(200, 200).astype(np.float32)

# 复制img_t0的内容到img_t1
img_t1 = img_t0.copy()

# 将img_t1旋转-1度
img_t1 = rotate_image(img_t1, -1)

# 可视化
fig1, (ax_1, ax_2) = plt.subplots(1, 2)
# 在ax_1中显示img_t0
ax_1.imshow(img_t0)
ax_1.set_title("Frame t0")
# 在ax_2中显示img_t1
ax_2.imshow(img_t1)
ax_2.set_title("Frame t1")
# 显示图像
plt.show()

接着，我们实现一个高斯滤波器对图像进行平滑处理以降低噪声影响，然后计算图像的梯度。

def smooth(img, sigma):
    """
    高斯平滑函数，返回平滑后的图像。

    参数:
    - img: 输入图像。
    - sigma: 高斯核的标准差。
    """
    # 创建x数组，范围为[-3sigma,3sigma]
    x = np.array(list(range(math.floor(-3.0 * sigma + 0.5), 
                            math.floor(3.0 * sigma + 0.5) + 1)))
    
    # 计算高斯核G
    G = np.exp(-x ** 2 / (2 * sigma ** 2))
    G = G / np.sum(G)

    # 对图像进行二维卷积
    return cv2.sepFilter2D(img, -1, G, G)


def gaussderiv(img, sigma):
    """
    高斯求导函数。

    参数:
    - param img: 输入图像。
    - param sigma: 高斯核的标准差。

    返回:
    - Dx: x轴方向的导数图像。
    - Dy: y轴方向的导数图像。
    """
    # 创建x数组，范围为[-3sigma,3sigma]
    x = np.array(list(range(math.floor(-3.0 * sigma + 0.5), 
                            math.floor(3.0 * sigma + 0.5) + 1)))

    # 计算高斯核G
    G = np.exp(-x ** 2 / (2 * sigma ** 2))
    G = G / np.sum(G)

    # 计算高斯求导核D
    D = -2 * (x * np.exp(-x ** 2 / (2 * sigma ** 2))) / ( \
                            np.sqrt(2 * math.pi) * sigma ** 3)
    D = D / (np.sum(np.abs(D)) / 2)

    # 分别对图像进行x方向和y方向二维卷积
    Dx = cv2.sepFilter2D(img, -1, D, G)
    Dy = cv2.sepFilter2D(img, -1, G, D)

    return Dx, Dy

def calculate_derivatives(img1, img2, smoothing, derivation):
    """
    计算图像的导数。

    参数:
    - img1: 前一帧图像。
    - img2: 后一帧图像。
    - smoothing: 高斯平滑的标准差。
    - derivation: 高斯求导的标准差。

    返回:
    - i_x: x轴方向的导数图像。
    - i_y: y轴方向的导数图像。
    - i_t: 时间方向的导数图像。
    """
    # 计算t方向导数
    i_t = smooth(img2 - img1, smoothing)
    # 计算x、y方向导数
    i_x, i_y = gaussderiv(smooth(np.divide(img1 + \
                                img2, 2), smoothing), derivation)
    return i_x, i_y, i_t

再根据得到的梯度分块计算区块内的光流。

def sum_kernel(x, N):
    '''
    计算块内和。
    '''
    return cv2.filter2D(x, -1, np.ones((N, N)))

def lucas_kanade(img1, img2, N, smoothing=1, derivation=0.4):
    """
    Lucas-Kanade算法。

    参数:
    - img1: 前一帧图像。
    - img2: 后一帧图像。
    - N: 块大小。
    - smoothing: 高斯平滑的标准差。
    - derivation: 高斯求导的标准差。

    返回:
    - u: x轴方向的速度图像。
    - v: y轴方向的速度图像。
    """
    # 计算图像导数
    i_x, i_y, i_t = calculate_derivatives(img1, img2, 
                              smoothing, derivation)
    
    # 计算i_x_t和i_y_t
    i_x_t = sum_kernel(np.multiply(i_x, i_t), N)
    i_y_t = sum_kernel(np.multiply(i_y, i_t), N)
    
    # 计算梯度的平方
    i_x_2 = sum_kernel(np.square(i_x), N)
    i_y_2 = sum_kernel(np.square(i_y), N)
    
    i_x_y = sum_kernel(np.multiply(i_x, i_y), N)
    
    # 计算平方和
    D = np.subtract(
        np.multiply(i_x_2, i_y_2),
        np.square(i_x_y)
    )

    D += 1e-5
    
    # 计算各块内的u, v
    u = np.divide(
        np.add(
            np.multiply(-i_y_2, i_x_t),
            np.multiply(i_x_y, i_y_t)
        ),
        D
    )

    v = np.divide(
        np.subtract(
            np.multiply(i_x_y, i_x_t),
            np.multiply(i_x_2, i_y_t)
        ),
        D
    )

    return u, v

至此，我们已经得到两张图像间的运动向量，接下来我们将其可视化出来。

def show_flow(U, V, ax):
    """
    根据提供的U,V绘制光流。
    """
    # 控制分块的大小
    scaling = 0.1 
    # 使用高斯平滑处理光流
    u = cv2.resize(smooth(U, 1.5), (0, 0), 
                           fx=scaling, fy=scaling)
    v = cv2.resize(smooth(V, 1.5), (0, 0), 
                           fx=scaling, fy=scaling)

    # 生成x,y的坐标矩阵
    x_ = (np.array(list(range(1, u.shape[1] + 1))) - 0.5) / scaling
    y_ = -(np.array(list(range(1, u.shape[0] + 1))) - 0.5) / scaling
    x, y = np.meshgrid(x_, y_)

    # 画箭头
    ax.quiver(x, y, -u * 5, v * 5)
    ax.set_aspect(1.)


def draw_optical_flow(image_1, image_2, 
                      normalizeImages=True, win_size=10):
    """
    计算图像之间的光流并将其显示出来。
    """
    # 归一化图像
    if normalizeImages:
        image_1 = image_1 / 255.0
        image_2 = image_2 / 255.0
    # 计算光流
    U_lk, V_lk = lucas_kanade(image_1, image_2, win_size)

    # 预先定义画布用于可视化
    fig2, (ax_11, ax_12, ax_13) = plt.subplots(1, 3, dpi=200)
    # 第一帧
    ax_11.imshow(image_1)
    ax_11.set_title("Frame t0")
    ax_11.axis('off')
    # 第二帧
    ax_12.imshow(image_2)
    ax_12.set_title("Frame t1")
    ax_12.axis('off')
    # 光流
    show_flow(U_lk, V_lk, ax_13)
    ax_13.set_title("Lucas-Kanade")
    ax_13.axis('off')
    # 画布布局
    fig2.tight_layout()
    plt.show()

我们将之前生成的图像和旋转后的图像进行光流计算。

draw_optical_flow(img_t0, img_t1, normalizeImages=False)

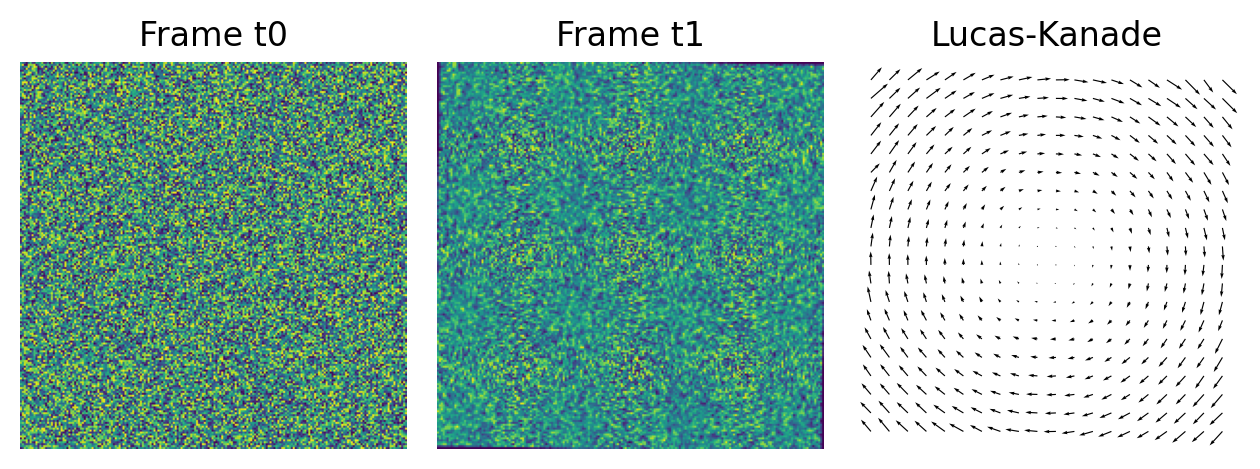
可以发现，Lucas-Kanade 算法在运动较小的情况下能够得到较好的效果。接下来让我们看看在运动较大的情况下，Lucas-Kanade 算法的效果如何。

img_t0 = np.random.rand(200, 200).astype(np.float32)
img_t1 = img_t0.copy()

# 测试运动较大的情况（旋转8度）
img_t1 = rotate_image(img_t1, -8) 
draw_optical_flow(img_t0, img_t1, normalizeImages=False)

可以看到当运动幅度较大时，相较于小幅度运动，Lucas-Kanade 算法的效果就不那么理想了。 接下来我们测试在真实的图像上的效果。

# !git clone https://github.com/boyu-ai/Hands-on-CV.git

image_1 = cv2.imread("learncv_img/optical_flow/frame_0001.png", 
                     cv2.IMREAD_GRAYSCALE).astype(np.float32)
image_2 = cv2.imread("learncv_img/optical_flow/frame_0002.png", 
                     cv2.IMREAD_GRAYSCALE).astype(np.float32)
# 绘制出光流图
draw_optical_flow(image_1, image_2, normalizeImages=True, win_size=15)

以上我们实现的是在全部像素上计算光流，在实际的运用过程中，一般是先检测角点，再进行光流的计算，这里我们使用OpenCV的calcOpticalFlowPyrLK函数来计算光流。

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 读取一段视频用于计算光流
cap = cv.VideoCapture(
    "./learncv_img/optical_flow/slow_traffic_small.mp4")
# ShiTomasi 角点检测参数
feature_params = dict(maxCorners = 100,
                       qualityLevel = 0.3,
                       minDistance = 7,
                       blockSize = 7 )
# Lucas-Kanade 光流法参数
lk_params = dict( winSize  = (15, 15),
    maxLevel = 2,
    criteria = (cv.TERM_CRITERIA_EPS | cv.TERM_CRITERIA_COUNT, 
                10, 0.03))
# 生成随机颜色用于描述光流
color = np.random.randint(0, 255, (100, 3))
# 读取第一帧并找到角点
ret, old_frame = cap.read()
old_gray = cv.cvtColor(old_frame, cv.COLOR_BGR2GRAY)
p0 = cv.goodFeaturesToTrack(old_gray, 
                    mask = None, **feature_params)
# 创建一个mask用于绘制轨迹
mask = np.zeros_like(old_frame)
while(1):
    ret, frame = cap.read()
    if not ret:
        print('No frames grabbed!')
        break
    frame_gray = cv.cvtColor(frame, cv.COLOR_BGR2GRAY)
    # 计算光流，并返回光流成功跟踪到的点p1，跟踪状态st以及跟踪差异err
    p1, st, err = cv.calcOpticalFlowPyrLK(old_gray, frame_gray, 
                                          p0, None, **lk_params)
    # 选择好的跟踪点
    if p1 is not None:
        # 筛选出跟踪成功的点
        good_new = p1[st==1]
        good_old = p0[st==1]

    # 绘制轨迹
    for i, (new, old) in enumerate(zip(good_new, good_old)):
        a, b = new.ravel()
        c, d = old.ravel()
        mask = cv.line(mask, (int(a), int(b)), (int(c), int(d)), \
                       color[i].tolist(), 2)
        frame = cv.circle(frame, (int(a), int(b)), 5, \
                          color[i].tolist(), -1)
        
    img = cv.add(frame, mask)
    # 更新上一帧的图像和跟踪点
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1, 1, 2)

# 显示结果
plt.imshow(cv.cvtColor(img, cv.COLOR_BGR2RGB))
plt.axis('off')
plt.show()

本文介绍了计算机视觉中的光流估计技术，重点阐述了运动场与光流的概念差异及其计算方法。主要内容包括：

1) 运动场表示三维运动在二维平面的投影，而光流是基于图像亮度变化的运动近似；

2) Lucas-Kanade光流法通过亮度恒定、微小移动和空间一致性假设求解光流方程，并介绍了迭代法和图像金字塔等改进方法；

3) 通过代码示例演示了Lucas-Kanade算法的实现过程，包括图像预处理、梯度计算和光流求解；4) 对比分析了特征点法和直接法的优缺点，并展示了在真实视频中应用OpenCV光流函数的效果。研究结果表明，光流估计在运动分析、目标跟踪等领域具有重要应用价值。