分治-归并-315.计算右侧小于当前元素的个数-力扣(LeetCode)

一、题目解析

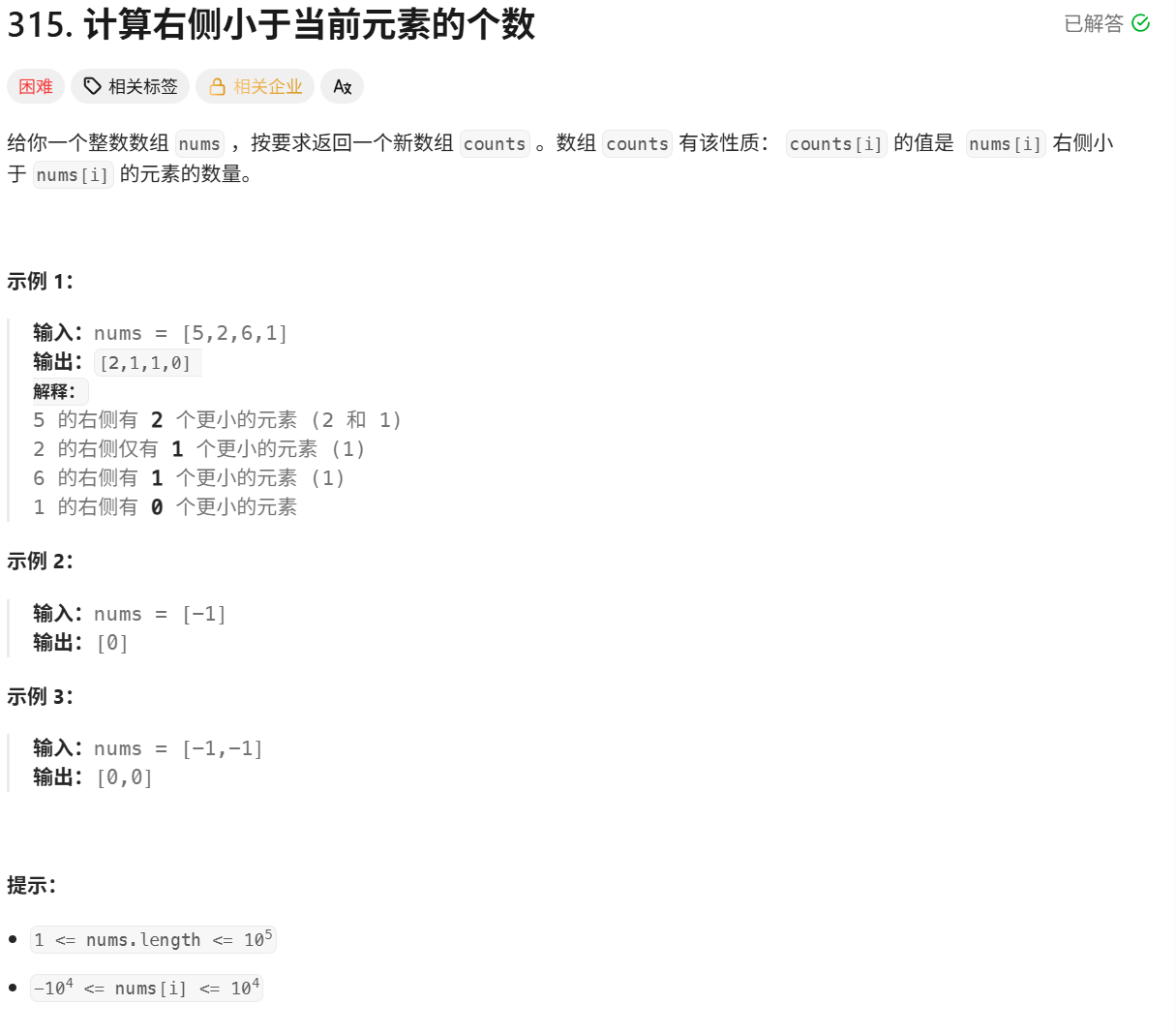
1、统计右侧小于当前元素的个数

2、将个数填入到与当前元素对应下边的结果数组中

3、nums的最大长度为10^5

二、算法原理

解法1：暴力解法(该解法必然超时，不过多赘述)

固定一个数，向后遍历扫描，时间复杂度O(N^2)

解法2：归并排序(分治)

对于一个数组，以中心mid划分，左端点记作left，右端点记作right，将其分为两块[left，mid]和[mid+1，right]，然后继续二分，直到只有一个元素时返回

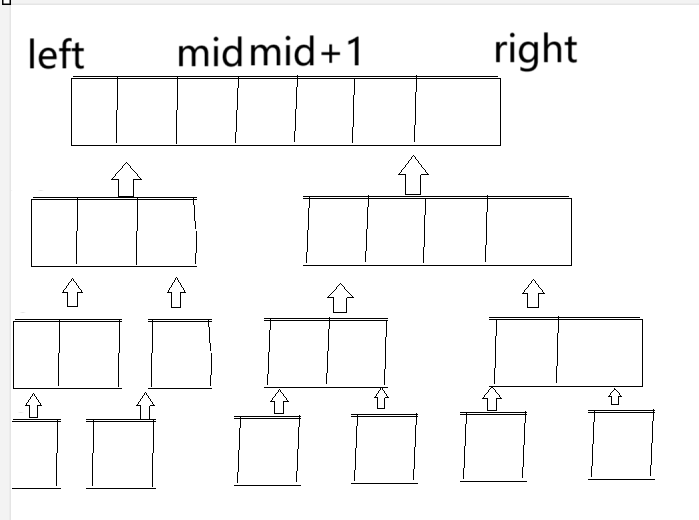
这里给出一个结论：记暴力遍历后所得小于当前元素个数为x，在分治中将数组分为两块，在左边所得小于当前元素个数为a，在右边所得小于当前元素个数为b，一左一右所得小于当前元素个数为c。x=a+b+c

证明也很好证明，我们左，右，一左一右的本质也是暴力遍历，只不过我们利用了分治-归并的思想

一左一右处理(元素成降序排列)

处理下标问题

由于处理下标，所以在上面排序时也需要对下标进行处理

细节问题：

1、返回结果的vector<int> ret，和int index[100005]，int tmpNums[100005]，     int tmpIndex[100005]，需要在全局开辟四个数组，为了节省参数传递

2、对于一左一右三指针处理，判断条件可能会导致某一区间未遍历完，所以需要特俗处理，并处理下标和元素

3、最后需要根据tmpNums和tmpIndex更新nums和index的内容

三、代码示例

解法2：

class Solution {
    vector<int> ret;
    int index[100005],tmpNums[100005],tmpIndex[100005];
public:
    vector<int> countSmaller(vector<int>& nums)
    {
        ret.resize(nums.size());
        for(int i = 0;i<nums.size();i++)
        {
            index[i] = i;//处理下标数组
        }
        mergeSort(nums,0,nums.size()-1);
        return ret;
    }
    void mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return;
        //分成两块
        int mid = (left+right)>>1;
        //分治
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);
        //一左一右
        int cur1 = left,cur2 = mid+1,i = 0;
        while(cur1<=mid && cur2<=right)
        {
            if(nums[cur1]<=nums[cur2])
            {
                tmpIndex[i] = index[cur2];
                tmpNums[i++] = nums[cur2++];
            }
            else
            {
                ret[index[cur1]] += right-cur2+1;
                tmpIndex[i] = index[cur1];
                tmpNums[i++] = nums[cur1++];
            }
        }
        //未完成遍历
        while(cur1<=mid)
        {
            tmpIndex[i] = index[cur1];
            tmpNums[i++] = nums[cur1++];
        }
        while(cur2<=right)
        {
            tmpIndex[i] = index[cur2];
           tmpNums[i++] = nums[cur2++];
        }
        //还原
        for(int i = left;i<=right;i++)
        {
            nums[i] = tmpNums[i-left];
            index[i] = tmpIndex[i-left];
        }
    }
};

看到最后，如果对您有所帮助，还请点赞、收藏和关注，我们下期再见！