Pyomo、PuLP 和 OR-Tools 解决约束优化问题效率对比

假设我们有三种原油类型：

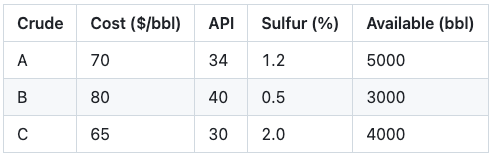
我们的任务是混合 6000 桶 原油，使其满足：

• API ≥ 35
• 硫含量 ≤ 1.0%
• 任何原油的用量不超过其可用量

在此场景中，我们的目标是最小化总成本。这可以根据需要改为最大化预期利润（成本与市场价格之间的差额），或者其他目标函数，例如最大化随时间变化的稳定性。

1 Pyomo

import pyomo.environ as pyo

model = pyo.ConcreteModel()
crudes = ['A', 'B', 'C']
cost = {'A': 70, 'B': 80, 'C': 65}
api = {'A': 34, 'B': 40, 'C': 30}
sulfur = {'A': 1.2, 'B': 0.5, 'C': 2.0}
avail = {'A': 5000, 'B': 3000, 'C': 4000}
model.crudes = pyo.Set(initialize=crudes)
model.vol = pyo.Var(model.crudes, domain=pyo.NonNegativeReals)
model.cost = pyo.Objective(expr=sum(model.vol[c] * cost[c] for c in crudes), sense=pyo.minimize)
model.total_volume = pyo.Constraint(expr=sum(model.vol[c] for c in crudes) == 6000)
model.sulfur = pyo.Constraint(expr=sum(model.vol[c]*sulfur[c] for c in crudes) <= 6000*1.0)
model.api = pyo.Constraint(expr=sum(model.vol[c]*api[c] for c in crudes) >= 6000*35)
model.avail = pyo.ConstraintList()
for c in crudes:
    model.avail.add(model.vol[c] <= avail[c])
solver = pyo.SolverFactory('glpk')
solver.solve(model)

优点： 建模语言丰富，易于扩展（非线性、MIP）
缺点： 略显冗长，需要外部求解器（GLPK, CBC）

2 PuLP

from pulp import *

model = LpProblem("CrudeBlend", LpMinimize)
vol = LpVariable.dicts("vol", ['A', 'B', 'C'], lowBound=0)
model += lpSum([vol[i] * cost[i] for i in crudes])
model += lpSum([vol[i] for i in crudes]) == 6000
model += lpSum([vol[i] * sulfur[i] for i in crudes]) <= 6000 * 1.0
model += lpSum([vol[i] * api[i] for i in crudes]) >= 6000 * 35
for i in crudes:
    model += vol[i] <= avail[i]
model.solve()

优点： 语法简洁，易于学习，内置 CBC 求解器
缺点： 对于非线性或大型模型功能较弱

3 OR-Tools

from ortools.linear_solver import pywraplp

solver = pywraplp.Solver.CreateSolver('GLOP')
vol = {i: solver.NumVar(0, avail[i], i) for i in crudes}
solver.Add(solver.Sum([vol[i] for i in crudes]) == 6000)
solver.Add(solver.Sum([vol[i]*sulfur[i] for i in crudes]) <= 6000 * 1.0)
solver.Add(solver.Sum([vol[i]*api[i] for i in crudes]) >= 6000 * 35)
solver.Minimize(solver.Sum([vol[i] * cost[i] for i in crudes]))
status = solver.Solve()

优点： 速度极快，适用于 Google 规模系统的生产环境
缺点： 语法灵活性较低，对非线性或符号模型的支持较弱

4 推荐

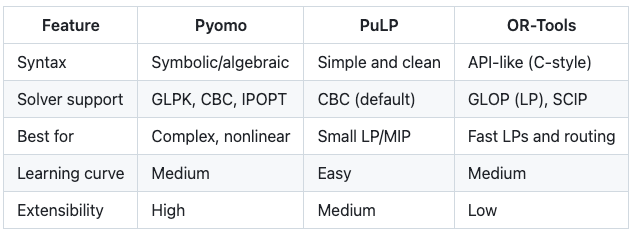
• 对于小型、易读的线性规划问题，使用 PuLP。
• 当建模更复杂、多阶段或非线性系统时，使用 Pyomo。
• 当需要速度、性能或路径规划时，使用 OR-Tools。

这是一个并排测试。问题很简单，但对于这个简单的问题，运行时差异之大令人惊讶。

import pyomo.environ as pyo
from pulp import *
from ortools.linear_solver import pywraplp
import time
import pandas as pd

crudes = ['A', 'B', 'C']
cost = {'A': 70, 'B': 80, 'C': 65}
api = {'A': 34, 'B': 40, 'C': 30}
sulfur = {'A': 1.2, 'B': 0.5, 'C': 2.0}
avail = {'A': 5000, 'B': 3000, 'C': 4000}
target_vol = 6000
sulfur_max = 1.0
api_min = 35

results = {}

start = time.time()
model_pyo = pyo.ConcreteModel()
model_pyo.crudes = pyo.Set(initialize=crudes)
model_pyo.vol = pyo.Var(model_pyo.crudes, domain=pyo.NonNegativeReals)
model_pyo.cost = pyo.Objective(expr=sum(model_pyo.vol[c] * cost[c] for c in crudes), sense=pyo.minimize)
model_pyo.total_volume = pyo.Constraint(expr=sum(model_pyo.vol[c] for c in crudes) == target_vol)
model_pyo.sulfur = pyo.Constraint(expr=sum(model_pyo.vol[c]*sulfur[c] for c in crudes) <= target_vol*sulfur_max)
model_pyo.api = pyo.Constraint(expr=sum(model_pyo.vol[c]*api[c] for c in crudes) >= target_vol*api_min)
model_pyo.avail = pyo.ConstraintList()
for c in crudes:
    model_pyo.avail.add(model_pyo.vol[c] <= avail[c])
solver = pyo.SolverFactory('glpk')
solver.solve(model_pyo)
end = time.time()
results['Pyomo'] = {
    'runtime_sec': round(end - start, 6),
    'volumes': {c: round(pyo.value(model_pyo.vol[c]), 2) for c in crudes},
    'cost': round(sum(pyo.value(model_pyo.vol[c]) * cost[c] for c in crudes), 2)
}

start = time.time()
model_pulp = LpProblem("CrudeBlend", LpMinimize)
vol_pulp = LpVariable.dicts("vol", crudes, lowBound=0)
model_pulp += lpSum([vol_pulp[i] * cost[i] for i in crudes])
model_pulp += lpSum([vol_pulp[i] for i in crudes]) == target_vol
model_pulp += lpSum([vol_pulp[i] * sulfur[i] for i in crudes]) <= target_vol * sulfur_max
model_pulp += lpSum([vol_pulp[i] * api[i] for i in crudes]) >= target_vol * api_min
for i in crudes:
    model_pulp += vol_pulp[i] <= avail[i]
model_pulp.solve()
end = time.time()
results['PuLP'] = {
    'runtime_sec': round(end - start, 6),
    'volumes': {c: round(vol_pulp[c].varValue, 2) for c in crudes},
    'cost': round(value(model_pulp.objective), 2)
}

start = time.time()
solver = pywraplp.Solver.CreateSolver('GLOP')
vol_ort = {i: solver.NumVar(0, avail[i], i) for i in crudes}
solver.Add(solver.Sum([vol_ort[i] for i in crudes]) == target_vol)
solver.Add(solver.Sum([vol_ort[i]*sulfur[i] for i in crudes]) <= target_vol * sulfur_max)
solver.Add(solver.Sum([vol_ort[i]*api[i] for i in crudes]) >= target_vol * api_min)
solver.Minimize(solver.Sum([vol_ort[i] * cost[i] for i in crudes]))
status = solver.Solve()
end = time.time()
results['OR-Tools'] = {
    'runtime_sec': round(end - start, 6),
    'volumes': {c: round(vol_ort[c].solution_value(), 2) for c in crudes},
    'cost': round(sum(vol_ort[c].solution_value() * cost[c] for c in crudes), 2)
}

df = pd.DataFrame(results).T

文章出自：Comparing Pyomo, PuLP, and OR-Tools for Constrained Optimization problems to find optimal crude oil blends

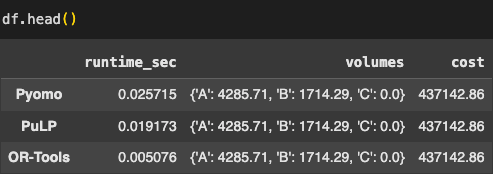
本篇文章适合对优化算法感兴趣的读者，特别是新手。亮点在于对三种优化工具（Pyomo、PuLP和OR-Tools）的详细比较，涵盖了各自的优缺点及适用场景，帮助用户选择合适的工具进行约束优化问题。

该方法适用于需要优化资源配置的场景，如石油混合、供应链管理等。实际案例展示了如何在约束条件下找到成本最低的原油混合方案，有助于提高决策效率和经济效益。