(LeetCode 每日一题) 3446. 按对角线进行矩阵排序（矩阵、排序）

题目：3446. 按对角线进行矩阵排序

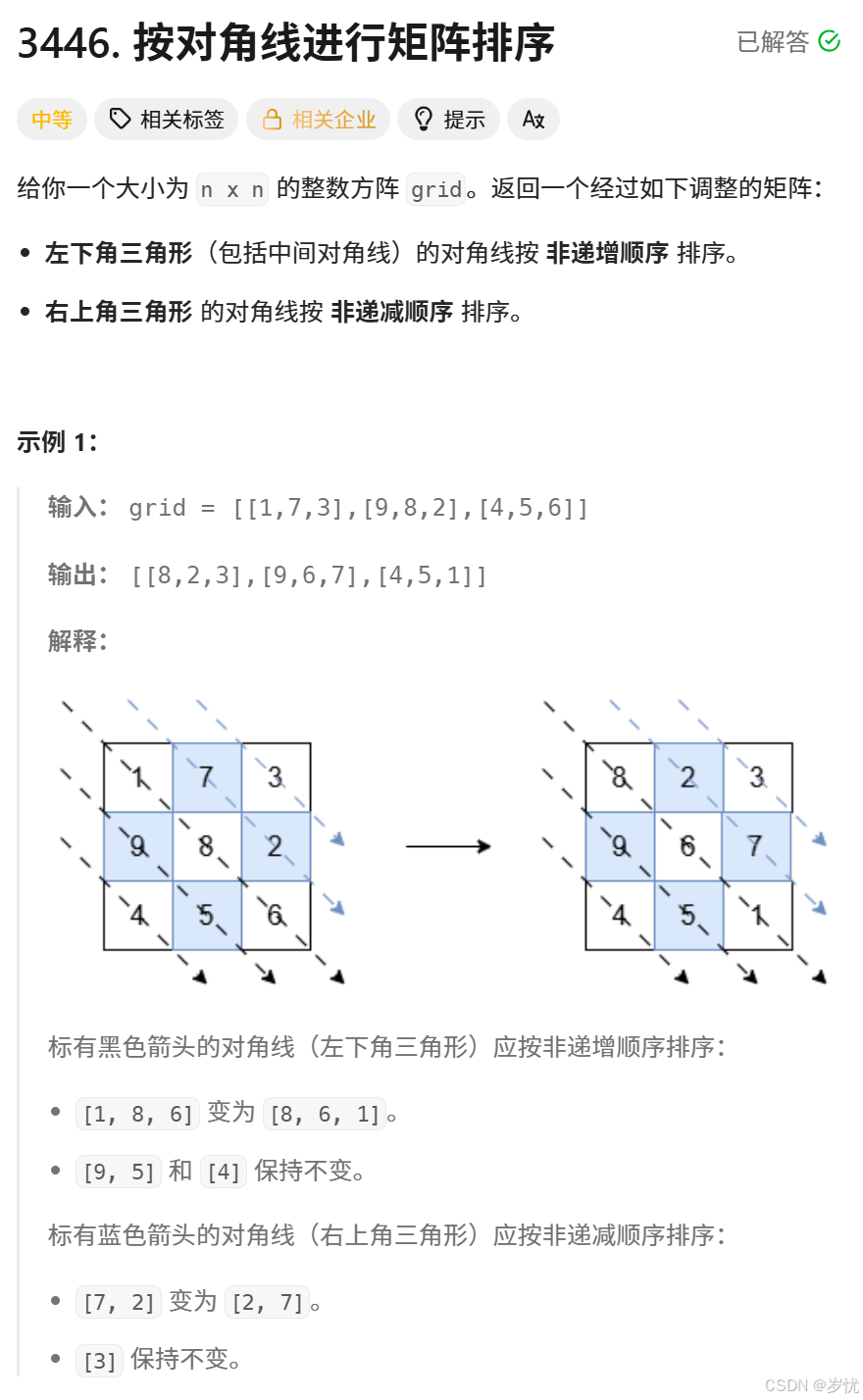
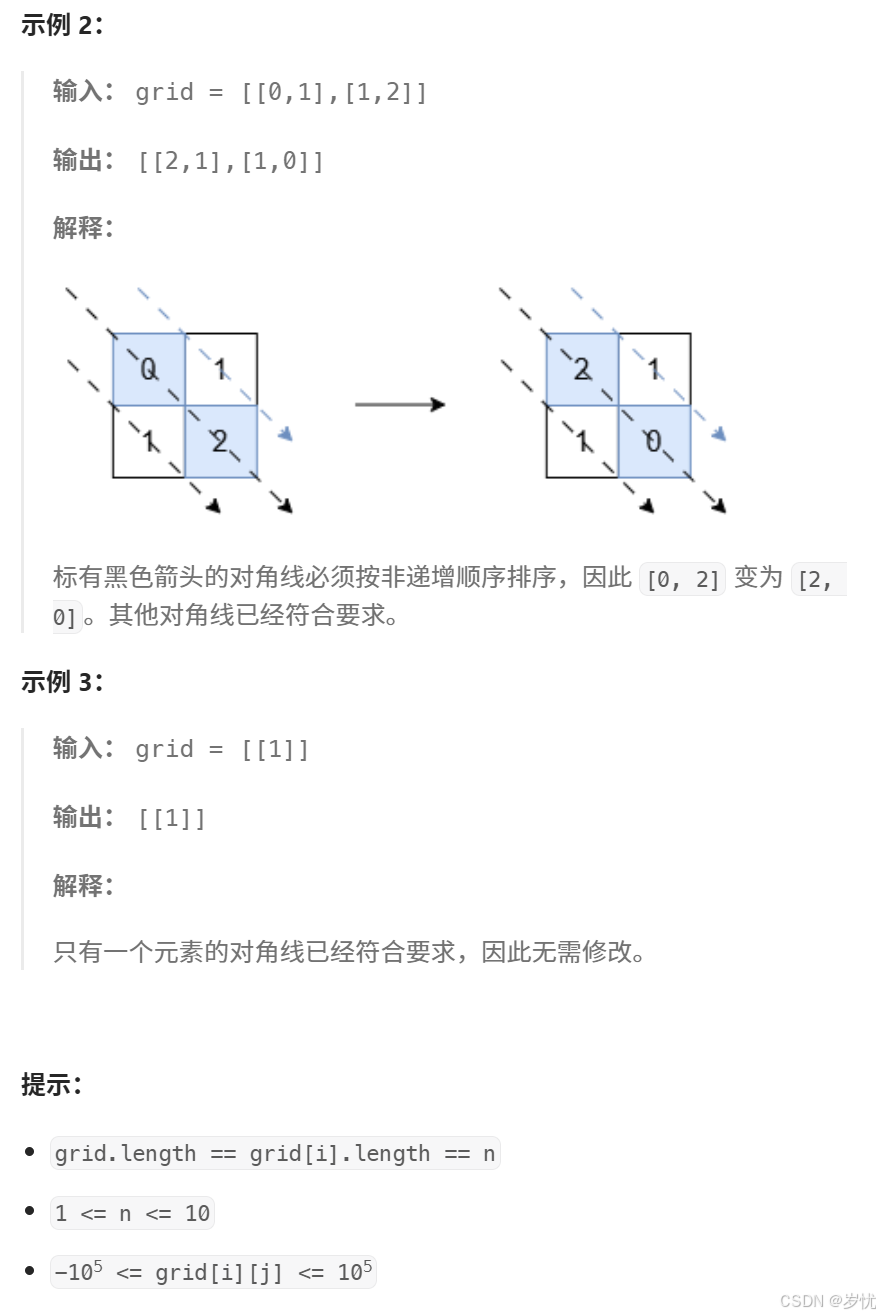
思路：矩阵+排序，时间复杂度0(n^2)。
每条对角线上的节点都符合 k=i-j+n ，而k的取值范围为((n-1)-0+n, 0-(n-1)+n)。

细节看注释

C++版本：

class Solution {
public:
    vector<vector<int>> sortMatrix(vector<vector<int>>& grid) {
        int n=grid.size();
        vector<vector<int>> ans(n,vector<int>(n,0));
        //确定k的取值范围
        // k=i-j+n -> k=(n-1)-0+n  k=0-(n-1)+n;
        for(int k=1;k<=2*n-1;k++){
            // j=i+n-k
            // 确定j的取值范围
            int mx=min(n-1,n-1+n-k);
            int mn=max(0,0+n-k);
            vector<int> v;
            for(int j=mn;j<=mx;j++){
                v.push_back(grid[k+j-n][j]);
            }
            //上半段都是升序(k<n)，下半段都是降序(k>=n)
            if(k<n) sort(v.begin(),v.end());
            else sort(v.begin(),v.end(),greater());
            for(int j=mn;j<=mx;j++){
               ans[k+j-n][j]=v[j-mn];
            }
        }
        return ans;
    }
};

JAVA版本：

class Solution {
    public int[][] sortMatrix(int[][] grid) {
        int n=grid.length;
        int[][] ans=new int[n][n];
        // k=i-j+n -> k=(n-1)-0+n  k=0-(n-1)+n;
        for(int k=1;k<=2*n-1;k++){
            // j=i+n-k
            int mx=Math.min(n-1,n-1+n-k);
            int mn=Math.max(0,0+n-k);
            List<Integer> v=new ArrayList<Integer>();
            for(int j=mn;j<=mx;j++){
                v.add(grid[k+j-n][j]);
            }
            if(k<n) Collections.sort(v);
            else Collections.sort(v,Collections.reverseOrder());
            for(int j=mn;j<=mx;j++){
               ans[k+j-n][j]=v.get(j-mn);
            }
        }
        return ans;
    }
}

GO版本：

func sortMatrix(grid [][]int) [][]int {
    n:=len(grid)
    ans:=make([][]int,n)
    for i:=0;i<n;i++ {
        ans[i]=make([]int,n)
    }
    // k=i-j+n -> k=(n-1)-0+n  k=0-(n-1)+n;
    for k:=1;k<=2*n-1;k++ {
        // j=i+n-k
        mx:=min(n-1,n-1+n-k)
        mn:=max(0,0+n-k)
        v:=make([]int,0)
        for j:=mn;j<=mx;j++ {
            v=append(v,grid[k+j-n][j])
        }
        slices.Sort(v)
        if k<n {
            for j:=mn;j<=mx;j++ {
                ans[k+j-n][j]=v[j-mn]
            }
        }else{
            m:=len(v)
            for j:=mn;j<=mx;j++ {
                ans[k+j-n][j]=v[m-(j-mn)-1]
            }
        }
    }
    return ans
}