目录
两独立样本t检验详解
一、设计思想与原理
1.1 基本概念
两独立样本t检验用于比较两个未知总体之间的差异,通过从两个总体中分别抽取样本进行统计分析。
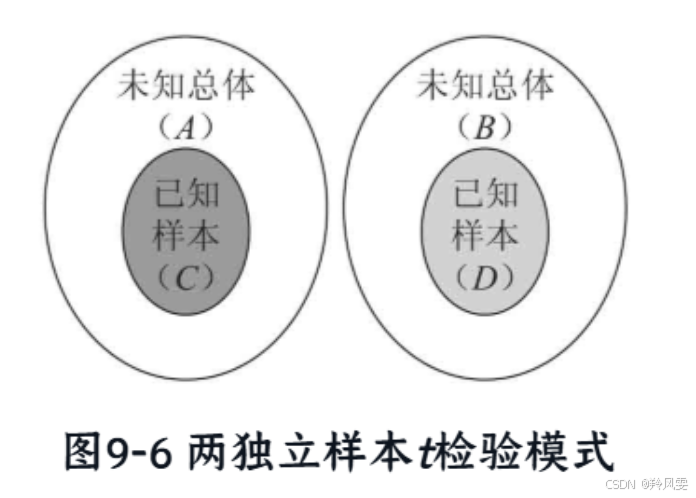
1.2 设计模式
形象比喻:"两个半个的鸭蛋"
核心特征:两个样本组相互独立,互不影响
1.3 样本获取方式
随机分组:将研究对象随机分配到两个处理组
示例:60只SD大鼠随机分为2组,每组30只,接受不同处理属性特征分组:按研究对象固有属性分组
示例:按性别分为男生组和女生组,比较考试成绩差异
二、案例实战分析
2.1 案例背景
研究对象:某高校590名大学生
分组方式:按性别分组(男生组/女生组)
研究指标:肺呼量(mL)
研究问题:男女生的肺呼量是否存在显著差异
2.2 数据特征分析
分组类型:属性特征分组(非随机分组)
数据独立性:男生组与女生组相互独立
数据类型:计量资料(连续变量)
符合"两个半个的鸭蛋"设计模式
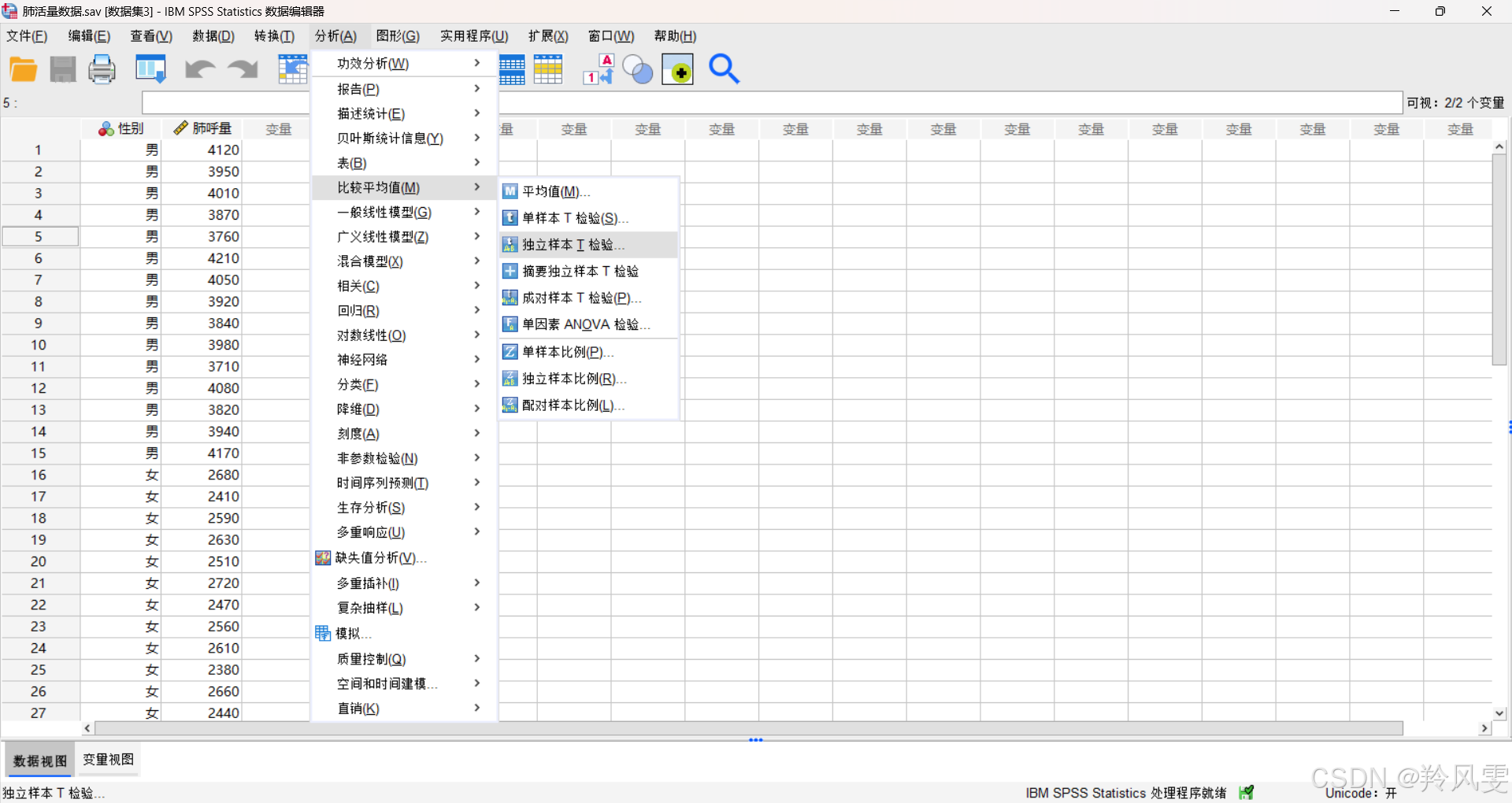
三、SPSS操作流程
菜单路径:分析 → 比较均值 → 独立样本t检验
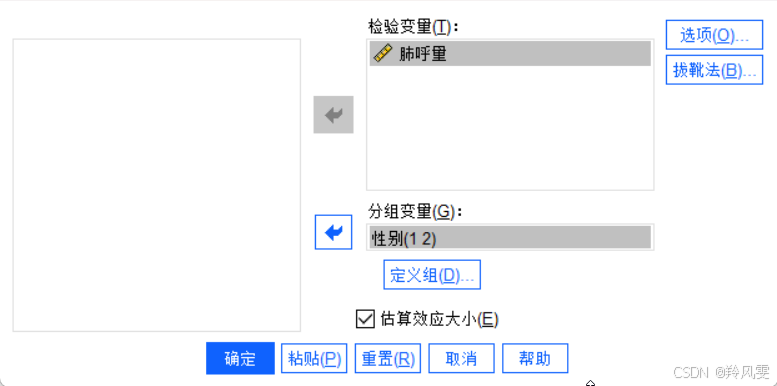
变量设置:
检验变量:肺呼量
分组变量:性别
组别定义:设置组1(男=1)和组2(女=2)
示例数据:30条
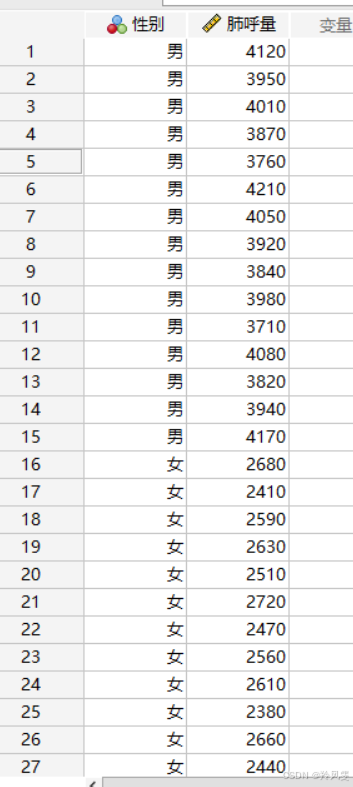
性别 肺呼量
男 4120
男 3950
男 4010
男 3870
男 3760
男 4210
男 4050
男 3920
男 3840
男 3980
男 3710
男 4080
男 3820
男 3940
男 4170
女 2680
女 2410
女 2590
女 2630
女 2510
女 2720
女 2470
女 2560
女 2610
女 2380
女 2660
女 2440
女 2530
女 2570
女 2480
数据特征:
模拟了男性肺呼量普遍高于女性的真实场景。
男性数据(~3800-4200 mL)和女性数据(~2400-2700 mL)的均值差异较大。
故意设置了两组的方差(离散程度)不同,以复现原文中“方差不齐”需要看校正结果的情况。
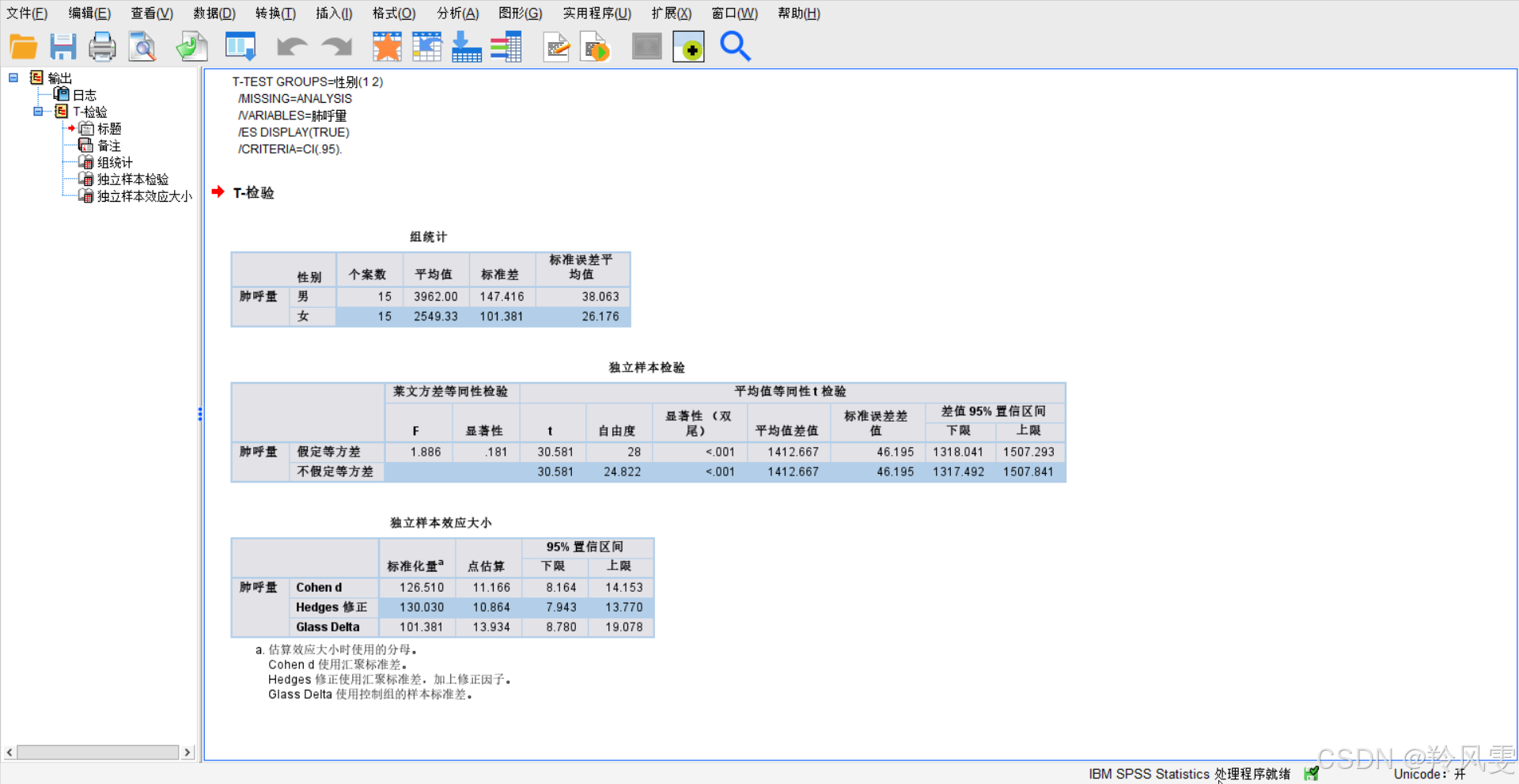
四、结果解读
这份结果分为三个主要表格:组统计、独立样本检验和独立样本效应大小。
一、组统计量(描述性统计)
| 性别 | 个案数 | 平均值 | 标准差 | 标准误差平均值 |
|---|---|---|---|---|
| 男 | 15 | 3962.00 | 147.416 | 38.063 |
| 女 | 15 | 2549.33 | 101.381 | 26.176 |
解读:
✔️ 样本量:男性和女性组各有15个样本,总样本量为30。样本量相等是很好的实验设计。
✔️ 平均值:男性的平均肺呼量为3962.00 mL,女性为2549.33 mL。男性的平均值远高于女性,差值高达1412.67 mL。这是我们观察到的“表面差异”。
✔️ 标准差:男性组的标准差(147.416)大于女性组(101.381),说明男性组数据的离散程度(个体差异)比女性组稍大。
❓ 核心问题:这个巨大的均值差异是真实存在的,还是仅仅由抽样误差导致的?这就需要接下来的假设检验(t检验)来回答。
二、独立样本检验(推断性统计)
这是最核心的表格,需要按照三步法进行解读。
第一步:方差齐性检验(Levene检验)
| F | 显著性 | |
|---|---|---|
| 假定等方差 | 1.886 | .181 |
解读:
✅ 目的:检查两个总体的方差是否相等,以决定我们应该看上面一行(假定等方差)还是下面一行(不假定等方差)的t检验结果。
✅ 假设:
零假设(H₀):两总体方差相等。
备择假设(H₁):两总体方差不相等。
✅ 结果:F = 1.886,显著性(Sig.) = 0.181
✅ 结论:由于p值(0.181) > 0.05的显著性水平,没有足够的证据拒绝零假设。我们认为两总体方差是齐的。
第二步:选择正确的t检验行
根据第一步的结论(方差齐性),我们应该选择第一行 “假定等方差” 的结果。
第三步:解读t检验结果(看“假定等方差”这一行)
| t | 自由度 | 显著性(双尾) | 平均值差值 | 标准误差差值 | 差值95%置信区间 | |
|---|---|---|---|---|---|---|
| 下限 | 上限 | |||||
| 30.581 | 28 | <.001 | 1412.667 | 46.195 | 1318.041 | 1507.293 |
解读:
✅ t值:t(28) = 30.581。t值非常大,意味着得到的样本均值差异远大于随机抽样误差可能带来的差异。
✅ 自由度:df = 28 (计算公式: n₁ + n₂ - 2 = 15 + 15 - 2)。
✅ 显著性(p值):p < .001 (或写作 p < 0.001)。这是一个极其显著的p值。
✅ 统计结论:由于p值远小于0.05的显著性水平,我们拒绝零假设。有极其显著的统计学证据表明,男性和女性的平均肺呼量存在差异。
✅ 平均值差值:1412.667 mL。这个值告诉我们,男性的肺呼量平均比女性高约1413 mL。
✅ 95%置信区间:[1318.041, 1507.293] mL。我们有95%的把握认为,两个总体均值的真实差异在这个区间范围内。注意:这个区间完全不包含0,这再次强有力地证明了差异确实存在。
三、独立样本效应大小(效果量)
效应大小用于衡量差异的实际意义或强度,它不受样本量大小的影响。
| 点估算 | 95%置信区间 | |
|---|---|---|
| Cohen‘s d | 11.166 | [8.164, 14.153] |
| Hedges’ g | 10.864 | [7.943, 13.770] |
解读:
✅ Cohen‘s d:这是最常用的效应量指标。d = 11.166。
✅ 效应量标准(Cohen提出的经验准则):
d ≈ 0.2→ 小效应d ≈ 0.5→ 中等效应d ≈ 0.8→ 大效应
✅ 结论:此处的d值高达11.166,这表示男性和女性在肺呼量上存在的不是一个简单的“大效应”,而是一个“巨大无比”的效应。这在生物学或医学上是完全合理的,因为生理结构决定了肺活量的性别差异非常大。
✅ Hedges’ g:g = 10.864。这是对Cohen‘s d的小样本修正,结果通常非常接近。结论相同。
✅ 置信区间:效应量的置信区间也非常宽且远离0,进一步证实了效应强度的可靠性。
最终总结
描述性统计:男性平均肺呼量(3962 mL)远高于女性(2549 mL)。
方差齐性:通过检验(p=0.181 > 0.05),满足t检验的方差齐性假设。
假设检验:独立样本t检验结果极其显著(
t(28) = 30.581, p < .001),拒绝零假设。结论:男性和女性的肺呼量存在统计学上的显著差异,男性的肺呼量显著高于女性。
效应量:这种差异不仅具有统计学意义,还具有巨大的实际意义(效应量Cohen’s d > 11)。
简单说:分析结果强有力地支持了“男生与女生的肺呼量有差异”的研究假设。
五、检验条件要求
5.1 独立性
要求:两组数据来自的总体相互独立
判定:由试验设计决定
重要性:必须满足的核心条件
5.2 正态性
要求:两组数据应符合正态分布
特点:相对宽松的条件
耐受性:t检验对近似正态或轻微偏态分布比较耐受
5.3 方差齐性
要求:两总体方差相等
特点:严格要求条件
处理原则:
方差齐:直接使用标准t检验
方差不齐:使用校正t'检验
六、核心要点总结
适用场景:比较两个独立组别的均值差异
前提条件:独立性必须满足,正态性相对宽松,方差齐性需要检验
结果解读:采用三步法(描述统计→方差齐性检验→t检验选择)
软件操作:注意正确设置分组变量和定义组别
实际应用:方差不齐时必须使用校正结果,确保结论准确性
七、注意事项
分组变量必须明确定义组别编码
方差齐性检验的P值决定使用哪一行t检验结果
即使描述性统计显示明显差异,也必须通过假设检验确认统计显著性
报告结果时应同时提供均值、标准差、t值和P值等完整信息