目录
牛客.小红的子串
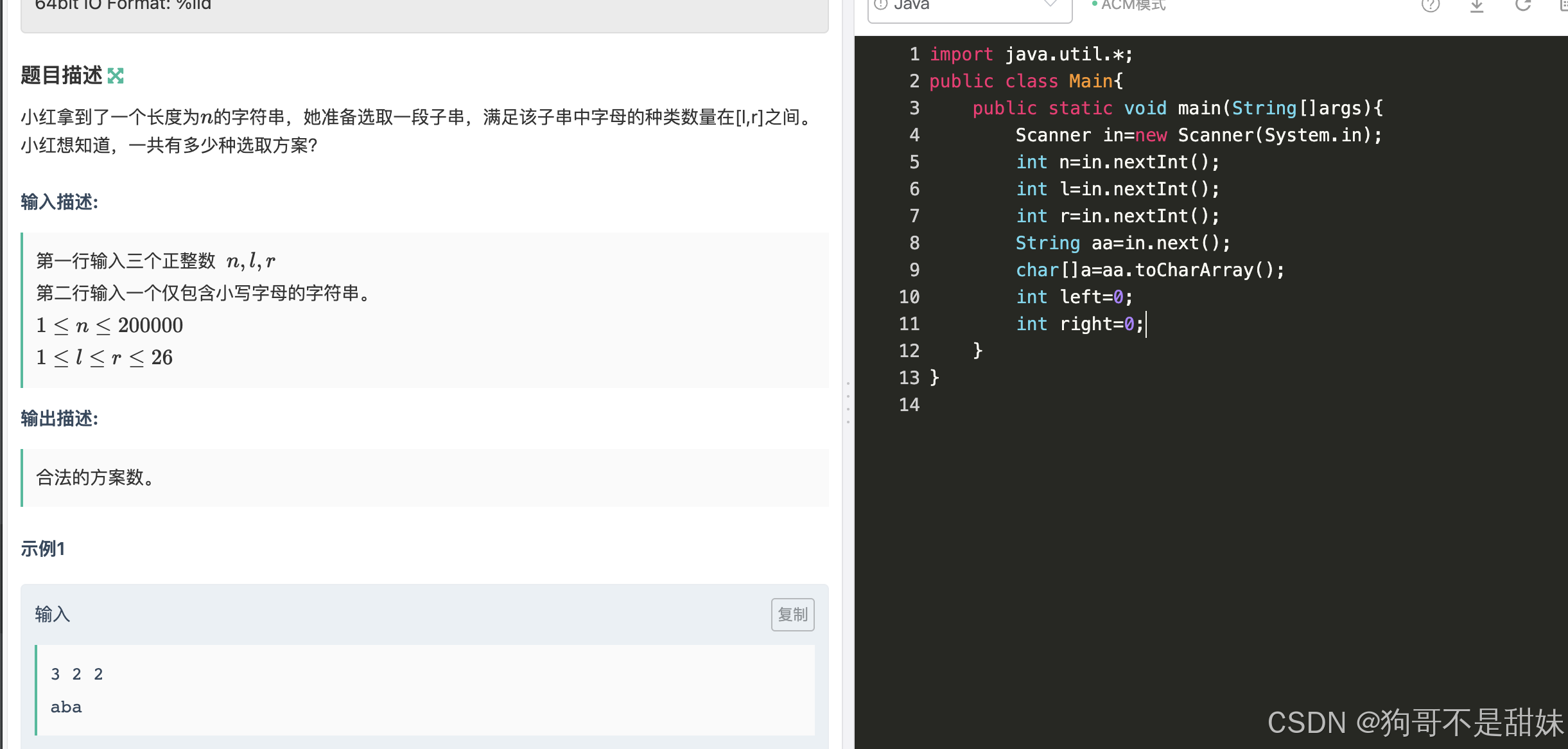
前缀和思想,l-r区间不好求,去求1-l,1-r,然后r-l
滑动窗口+前缀和思想
牛客.kotori和抽卡
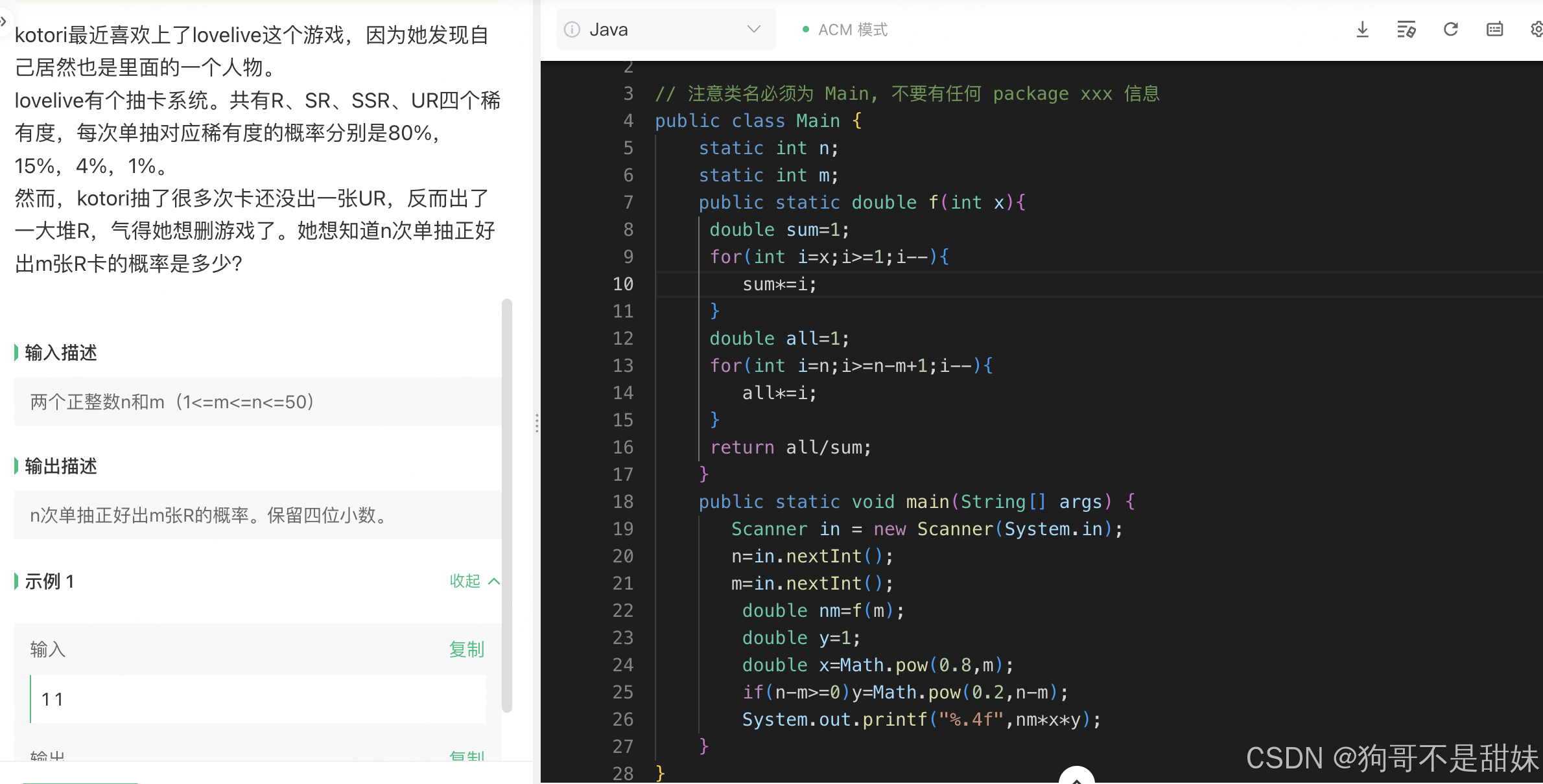
她这个数学公式,纯纯,但是我没想明白,
她这个应该是只看R的个数
我的意思是Cm^n (不需要你Cm^n之后,再算一下Cn-m^n)*R的m次幂,(1-R)的n-m次幂
import java.util.Scanner; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { static int n; static int m; public static double f(int x){ double sum=1; for(int i=x;i>=1;i--){ sum*=i; } double all=1; for(int i=n;i>=n-m+1;i--){ all*=i; } return all/sum; } public static void main(String[] args) { Scanner in = new Scanner(System.in); n=in.nextInt(); m=in.nextInt(); double nm=f(m); double y=1; double x=Math.pow(0.8,m); if(n-m>=0)y=Math.pow(0.2,n-m); System.out.printf("%.4f",nm*x*y); } }
牛客.循环汉诺塔
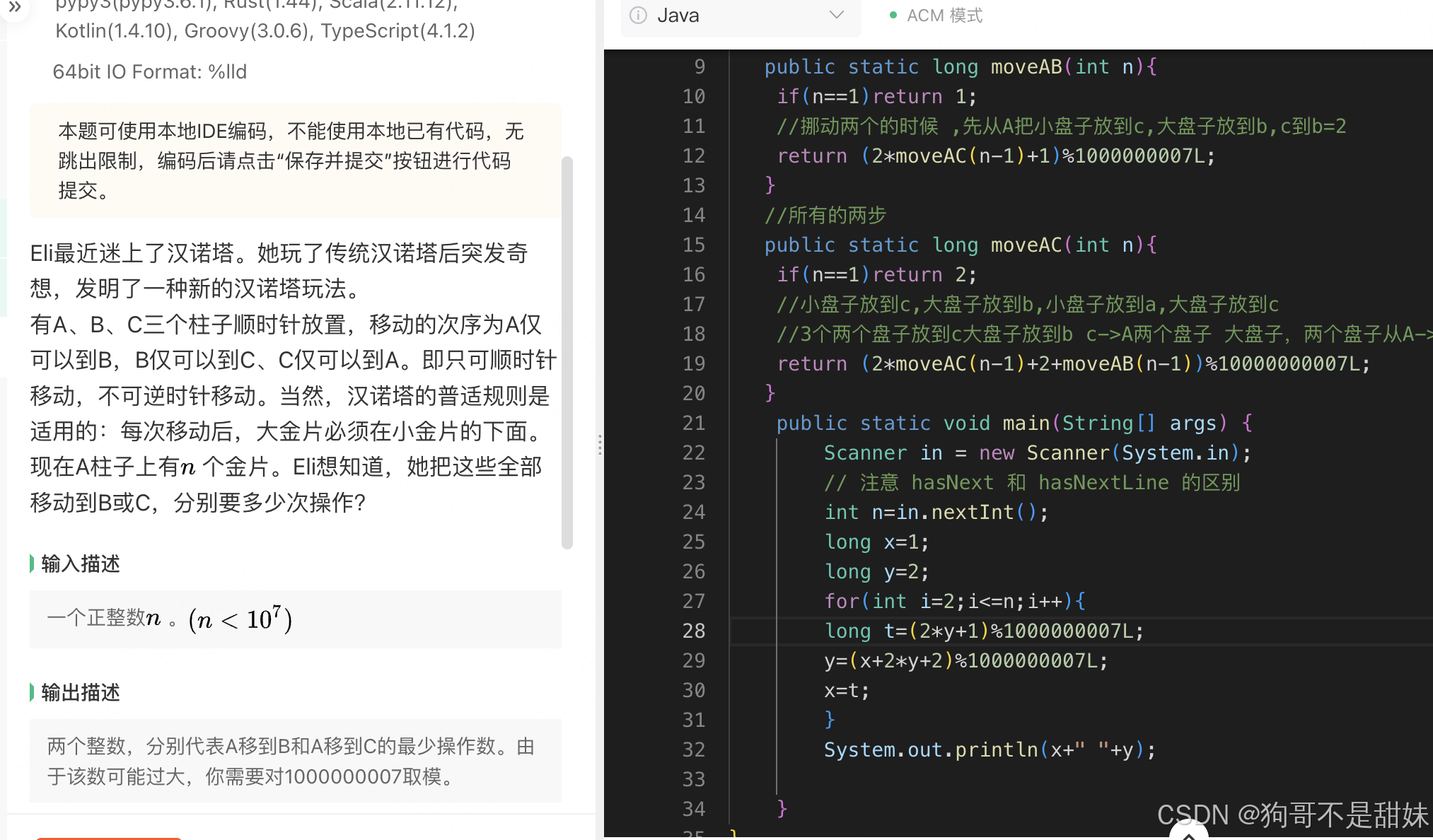
这个题也很有趣,汉诺塔,按照之前的方式思考,老花眼这道题那个不能复制真是抽象
考虑n=2,n=3依次考虑
x为一步,y为两步假如设置这个函数
假如从A移动到B,需要把其他的盘子先放到C,然后A的盘子放到B然后再去从C->B
一个2步( )+1步(跟盘子个数没关系,最后一定是移动一个盘子)+2步(. )
2*moveAC()代表2步的步数
从A移动到C,先把n-1个盘子放到C,然后大盘子放到B(一个盘子,不能省略),再去把 C的盘子放到A(一步(n-1)个) ,然后B移动到C(一步,一个盘子),然后再去把A的盘子放回到C(n-1个盘子)
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
// 把A上的片,下一个步骤是 Bn-1个,c一个, x+2
// 或者 A1个 ,Cn-1个 y+2
//n代表1个盘子
//从A到b代表所有的一步
public static long moveAB(int n){
if(n==1)return 1;
//挪动两个的时候 ,先从A把小盘子放到c,大盘子放到b,c到b=2
return (2*moveAC(n-1)+1)%1000000007L;
}
//所有的两步
public static long moveAC(int n){
if(n==1)return 2;
//小盘子放到c,大盘子放到b,小盘子放到a,大盘子放到c
//3个两个盘子放到c大盘子放到b c->A两个盘子 大盘子,两个盘子从A->C
return (2*moveAC(n-1)+2+moveAB(n-1))%10000000007L;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
int n=in.nextInt();
long x=1;
long y=2;
for(int i=2;i<=n;i++){
long t=(2*y+1)%1000000007L;
y=(x+2*y+2)%1000000007L;
x=t;
}
System.out.println(x+" "+y);
}
}牛客.ruby和薯条
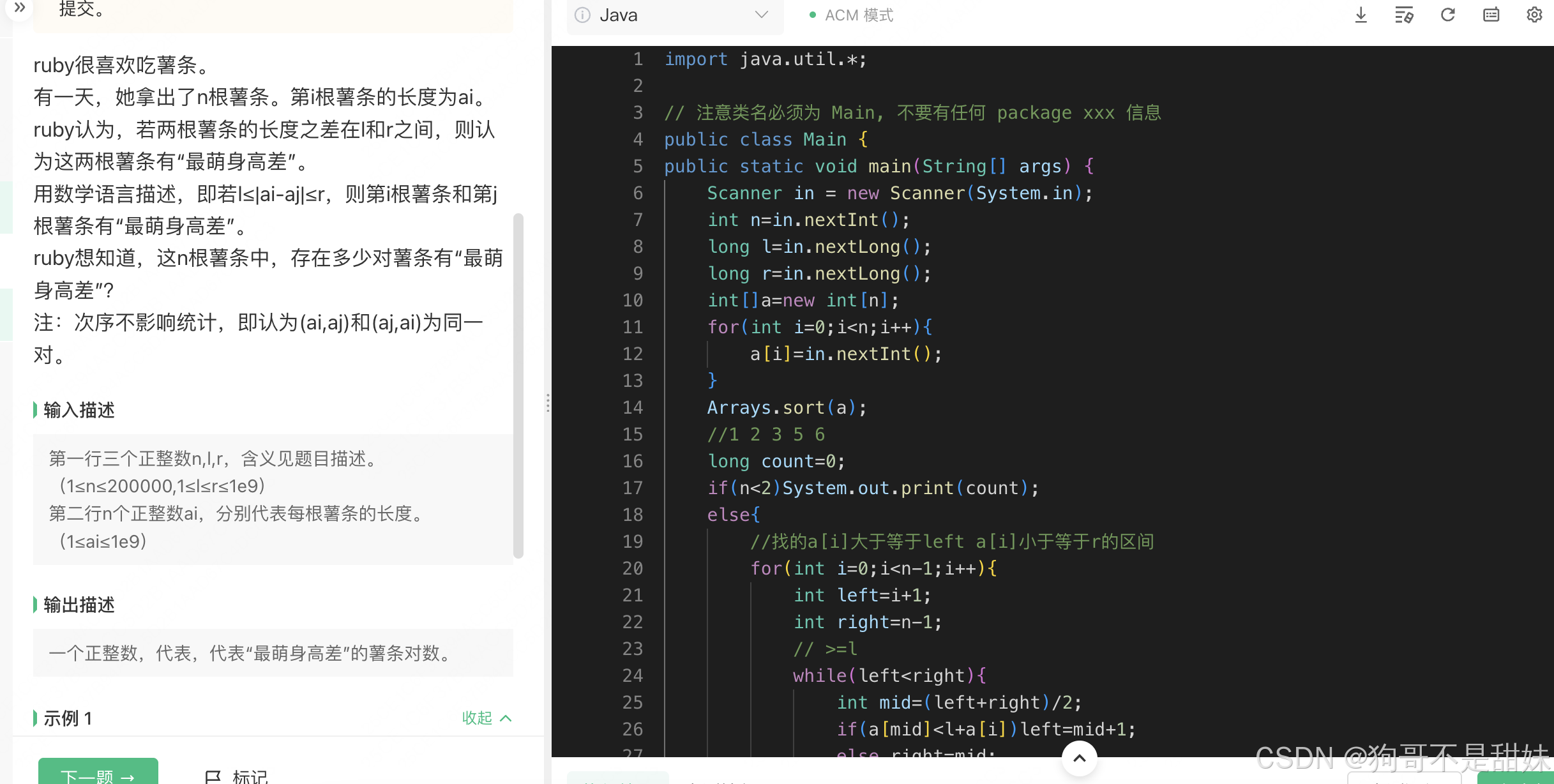
正常暴力,O(n^2)不行,所以,使用排序+二分,然后把看a[i] 把a[i]的left和right区间找到
import java.util.*; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); int n=in.nextInt(); long l=in.nextLong(); long r=in.nextLong(); int[]a=new int[n]; for(int i=0;i<n;i++){ a[i]=in.nextInt(); } Arrays.sort(a); //1 2 3 5 6 long count=0; if(n<2)System.out.print(count); else{ //找的a[i]大于等于left a[i]小于等于r的区间 for(int i=0;i<n-1;i++){ int left=i+1; int right=n-1; // >=l while(left<right){ int mid=(left+right)/2; if(a[mid]<l+a[i])left=mid+1; else right=mid; } int le=left; // <=r left=i+1; right=n-1; //二分细节 右端点 ,那个进行+1/-1. 那么他就不包含等于. while(left<right){ int mid=(left+right+1)/2; if(a[mid]>a[i]+r) right=mid-1; else left=mid; } //最后需要判断一下,是否真的符合区间要求,因为他有可能出现我都不进去循环,最后,left和right是相等的,然后明明不符合区间,却能满足要求。 所以最后一个需要进行判断,(但是不是说相等不对,是说相等的,但是我不进入循环,导致没有判断是否符合区间) if(a[right]-a[i]<=r&&a[le]-a[i]>=l)count+=right-le+1; } System.out.print(count); } } }
策略二,和之前一样,它是需要前缀和的思想,求出r和l-1区间,然后相减就好,right-left还是right-left+1要考虑一下, right-left+1 123 假如是这个区间,我们right是3,left是2,他是求的是,到达right,以right结尾的有多少个满足的,【1,3】 ,【2,3】right -left此时就是两个,然后加入说是right=left此时思考一下不具备一对的条件。
//1-r 1-l-1
static int n;
static int[]a;
public static long f(long x){
int left=0;
int right=0;
long ret=0;
while(right<n){
while(a[right]-a[left]>x){left++;}
ret+=right-left;
right++;
}
return ret;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n=in.nextInt();
long l=in.nextLong();
long r=in.nextLong();
a=new int[n];
for(int i=0;i<n;i++){
a[i]=in.nextInt();
}
Arrays.sort(a);
//1 2 3 5 6
long count=0;
if(n<2)System.out.print(count);
else{
//前缀和思想,求 0-l-1 和0-1-r
System.out.print(f(r)-f(l-1));
}
}