webrtc之高通滤波——HighPassFilter源码及原理分析-EW帮帮网

前言

webrtc中的高通滤波器可以大幅抑制 100 Hz 以下的频率成分（如 50 Hz 电源噪声、低频杂音等），其核心使用一个二阶IIR高通滤波器过滤低频分量。

本篇文章中，将先对于HighPassFilter的创建和使用配置以及整体的使用流程做一个梳理，然后再深入介绍算法实现，并且会使用matlab画出对应的通带、阻带、以及过渡带方便直观理解。

|版本声明：山河君，未经博主允许，禁止转载

一、导读

在 WebRTC 的语音处理链路中，高通滤波器（High Pass Filter，HPF）几乎是必备的一环。它的作用很直接：削弱 100Hz 以下的低频成分，比如电源嗡声、桌面震动、风扇噪声等，从而保证后续 AGC、NS、AEC 模块处理的信号更干净。

触发方式：
可以手动配置开启，也可能因为启用 AEC 等模块而被自动启用。
算法原理：
HPF 基于二阶 IIR 滤波器实现，每个通道/子带独立滤波。核心公式：
$y[n]=b_0x[n]+b_1x[n-1]+b_2x[n-2]-a_1y[n-1]-a_2y[n-2]$
滤波器系数：
根据采样率（16k/32k/48k）选择不同的 Butterworth 滤波器参数，保证截止频率在 ~100Hz。
实现特点：
- 使用 CascadedBiQuadFilter 串联二阶滤波器
- 支持全频带或子带处理
- 性能开销低，适合实时语音处理

二、高通滤波过程

1.HighPassFilter的创建

1）HighPassFilter的作用

HighPassFilter是用于去除音频输入中的低频噪声（如风声、风扇、桌面震动等）。例如：在会议中，麦克风经常会录到桌子震动的‘嗡嗡声’，WebRTC 的高通滤波器就是专门干掉这种低频噪声的。

这个配置常用于语音增强处理链（如 AGC、NS、AEC）之前。

2）开启条件

在 WebRTC 中，主动使用配置项 config.high_pass_filter.enabled = true 可以开启高通滤波器（High Pass Filter，HPF）。但如果不主动配置，同样有可能会默认打开高通滤波，如下代码：

void AudioProcessingImpl::InitializeHighPassFilter(bool forced_reset) {
  bool high_pass_filter_needed_by_aec =
      config_.echo_canceller.enabled &&
      config_.echo_canceller.enforce_high_pass_filtering &&
      !config_.echo_canceller.mobile_mode;
  if (submodule_states_.HighPassFilteringRequired() ||
      high_pass_filter_needed_by_aec) {
    bool use_full_band = config_.high_pass_filter.apply_in_full_band &&
                         !constants_.enforce_split_band_hpf;
    int rate = use_full_band ? proc_fullband_sample_rate_hz()
                             : proc_split_sample_rate_hz();
    size_t num_channels =
        use_full_band ? num_output_channels() : num_proc_channels();

    if (!submodules_.high_pass_filter ||
        rate != submodules_.high_pass_filter->sample_rate_hz() ||
        forced_reset ||
        num_channels != submodules_.high_pass_filter->num_channels()) {
      submodules_.high_pass_filter.reset(
          new HighPassFilter(rate, num_channels));
    }
  } else {
    submodules_.high_pass_filter.reset();
  }
}

例如在开启AEC时，会默认打开高通滤波，这只会影响高通滤波在3A处理时的顺序。

3）开启配置

HighPassFilter创建时受到采样率和通道数的影响，具体代码如下：

HighPassFilter::HighPassFilter(int sample_rate_hz, size_t num_channels)
    : sample_rate_hz_(sample_rate_hz) {
  filters_.resize(num_channels);
  const auto& coefficients = ChooseCoefficients(sample_rate_hz_);
  for (size_t k = 0; k < filters_.size(); ++k) {
    filters_[k].reset(
        new CascadedBiQuadFilter(coefficients, kNumberOfHighPassBiQuads));
  }
}

ChooseCoefficients(sample_rate_hz_)：根据采样率确定滤波器系数
new CascadedBiQuadFilter：根据通道数确定创建滤波器个数，同时滤波器获得系数

在本文中，将以采样率为16k，单通道为例进行介绍

2.高通滤波整体过程

1）触发时机

上文中已经说过，在不同条件下创建的HighPassFilter将会在不同时机进行高通滤波，以在处理近端采集信号做增益之前触发高通滤波举例：

if (submodules_.high_pass_filter &&
      (!config_.high_pass_filter.apply_in_full_band ||
       constants_.enforce_split_band_hpf)) {
    submodules_.high_pass_filter->Process(capture_buffer,
                                          /*use_split_band_data=*/true);
  }

其中满足以下两个条件时会进行高通滤波器

submodules_.high_pass_filter 不为空（即高通滤波器模块已经初始化）
满足以下任意一个：
- !config_.high_pass_filter.apply_in_full_band ：表示不在 full-band 上应用 HPF
- constants_.enforce_split_band_hpf 为真：强制在 split-band 上应用 HPF。

对于条件二，是判断是否进行了频带分割对于全频带或者各个子频道分别做高通滤波，而默认是对于各个子带做高通滤波的

2）滤波器创建

HPF滤波器真正创建构造函数有两种方式：

CascadedBiQuadFilter::CascadedBiQuadFilter(
    const CascadedBiQuadFilter::BiQuadCoefficients& coefficients,
    size_t num_biquads)
    : biquads_(num_biquads, BiQuad(coefficients)) {}

CascadedBiQuadFilter::CascadedBiQuadFilter(
    const std::vector<CascadedBiQuadFilter::BiQuadParam>& biquad_params) {
  for (const auto& param : biquad_params) {
    biquads_.push_back(BiQuad(param));
  }
}

前者是根据给定滤波器系数创建，后者是根据给定零极点计算出滤波器系数，具体的参数下文中会详细介绍。

3）高通滤波过程

在webrtc之子带分割下——SplittingFilter源码分析文章中，对于频带分割规则有过详细介绍：

对于32k采样率应该划分为两个子带
对于48k采样率应该分为三个自带
对于16k采样率不划分子带

而在使用HPF过程中，会默认对于每个通道的每个子带进行高通滤波，如以下代码

void HighPassFilter::Process(AudioBuffer* audio, bool use_split_band_data) {
  RTC_DCHECK(audio);
  RTC_DCHECK_EQ(filters_.size(), audio->num_channels());
  if (use_split_band_data) {
    for (size_t k = 0; k < audio->num_channels(); ++k) {
      rtc::ArrayView<float> channel_data = rtc::ArrayView<float>(
          audio->split_bands(k)[0], audio->num_frames_per_band());
      filters_[k]->Process(channel_data);
    }
  } else {
    for (size_t k = 0; k < audio->num_channels(); ++k) {
      rtc::ArrayView<float> channel_data =
          rtc::ArrayView<float>(&audio->channels()[k][0], audio->num_frames());
      filters_[k]->Process(channel_data);
    }
  }
}

而对于16k，单通道的音频信号，只需要进行一次滤波即可，具体的算法进行下文会详细介绍。

三、算法实现

1.原理

1）滤波器种类

CascadedBiQuadFilter是一种二阶的IIR滤波器，并且会根据创建时的参数来指定是否进行串联，如下文参数中：

根据给定滤波器系数创建：num_biquads参数指定串联个数
根据给定零极点计算创建：std::vector<CascadedBiQuadFilter::BiQuadParam>个数决定串联个数

在本文中，创建时传入的是给定的滤波器系数，并且指定滤波器个数为：

constexpr size_t kNumberOfHighPassBiQuads = 1;

根据二阶IIR滤波器差分方程，见文章语音信号处理六——递归/非递归离散时间系统与差分方程：
$y[n]=b_0x[n]+b_1x[n-1]+b_2x[n-2]-a_1y[n-1]-a_2y[n-2]$
而结构体BiQuadCoefficients 保存滤波器系数

struct BiQuadCoefficients {
    float b[3];
    float a[2];
  };

2）给定系数创建滤波器

根据采样率确定：

const CascadedBiQuadFilter::BiQuadCoefficients& ChooseCoefficients(
    int sample_rate_hz) {
  switch (sample_rate_hz) {
    case 16000:
      return kHighPassFilterCoefficients16kHz;
    case 32000:
      return kHighPassFilterCoefficients32kHz;
    case 48000:
      return kHighPassFilterCoefficients48kHz;
    default:
      RTC_NOTREACHED();
  }
  RTC_NOTREACHED();
  return kHighPassFilterCoefficients16kHz;
}

其中根据奎纳斯采样定理：

16k采样率过滤保留：100Hz~8kHz频率分量
32k采样率过滤保留：100Hz~16kHz频率分量
48k采样率过滤保留：100Hz~24kHz频率分量

滤波器系数如下：

// [B,A] = butter(2,100/8000,'high')
constexpr CascadedBiQuadFilter::BiQuadCoefficients
    kHighPassFilterCoefficients16kHz = {{0.97261f, -1.94523f, 0.97261f},
                                        {-1.94448f, 0.94598f}};

// [B,A] = butter(2,100/16000,'high')
constexpr CascadedBiQuadFilter::BiQuadCoefficients
    kHighPassFilterCoefficients32kHz = {{0.98621f, -1.97242f, 0.98621f},
                                        {-1.97223f, 0.97261f}};

// [B,A] = butter(2,100/24000,'high')
constexpr CascadedBiQuadFilter::BiQuadCoefficients
    kHighPassFilterCoefficients48kHz = {{0.99079f, -1.98157f, 0.99079f},
                                        {-1.98149f, 0.98166f}};

3）给定零极点创建滤波器

值得注意的是，创建高通滤波器时不会使用到这种方式。

根据二阶IIR滤波器传递函数，见文章语音信号处理十三——Z变换二（有理z变换、稳定性与反变换）：
$H(z)=\frac{b_0+b_1z^{-1}+b_2z^{-2}}{1+a_0z^{-1}+a_1z^{-2}}$
而对于代码中


CascadedBiQuadFilter::BiQuad::BiQuad(
    const CascadedBiQuadFilter::BiQuadParam& param)
    : x(), y() {
  float z_r = std::real(param.zero);
  float z_i = std::imag(param.zero);
  float p_r = std::real(param.pole);
  float p_i = std::imag(param.pole);
  float gain = param.gain;

  if (param.mirror_zero_along_i_axis) {
    // Assuming zeroes at z_r and -z_r.
    RTC_DCHECK(z_i == 0.f);
    coefficients.b[0] = gain * 1.f;
    coefficients.b[1] = 0.f;
    coefficients.b[2] = gain * -(z_r * z_r);
  } else {
    // Assuming zeros at (z_r + z_i*i) and (z_r - z_i*i).
    coefficients.b[0] = gain * 1.f;
    coefficients.b[1] = gain * -2.f * z_r;
    coefficients.b[2] = gain * (z_r * z_r + z_i * z_i);
  }

  // Assuming poles at (p_r + p_i*i) and (p_r - p_i*i).
  coefficients.a[0] = -2.f * p_r;
  coefficients.a[1] = p_r * p_r + p_i * p_i;
}

其中：

z_r ,z_i：是零点位置
p_r ,p_i ：是极点位置
gain ,p_i ：是极点位置
mirror_zero_along_i_axis：是否沿虚轴镜像零点（实数对称）

零点位置

零点沿虚轴镜像（ $z$ 与 $- z$ ），其传递函数分子为：
$1-z_rz^{-1})(1+z_rz^{-1})=1-z_r^2z^{-2}$
那么对应系数为：

b[0] = gain * 1.f;
b[1] = 0.f;
b[2] = gain * -(z_r * z_r);

常规复共轭零点（ $z=z_r\pm z_i i$ ），其传递函数分母为：
$1-(z_r+jz_i)z^{-1})(1+(z_r-jz_i)z^{-1})=1-2z_r^2z^{-1}+(z_r^2+z_i^2)z^{-1}$
那么对应的系数为

else {
  coefficients.b[0] = gain * 1.f;
  coefficients.b[1] = gain * -2.f * z_r;
  coefficients.b[2] = gain * (z_r * z_r + z_i * z_i);
}

极点位置

极点部分 $(p_r \pm p_i*i)$ 为复共轭，直接用共轭复数对展开，其传递函数分母为：
$1-2p_rz^{-1}+(p_r^2+p_i^2)z^{-2}$

  coefficients.a[0] = -2.f * p_r;
  coefficients.a[1] = p_r * p_r + p_i * p_i;

2.matlab分析

对于给定滤波器系数，使用matlab画出幅频响应如下图：
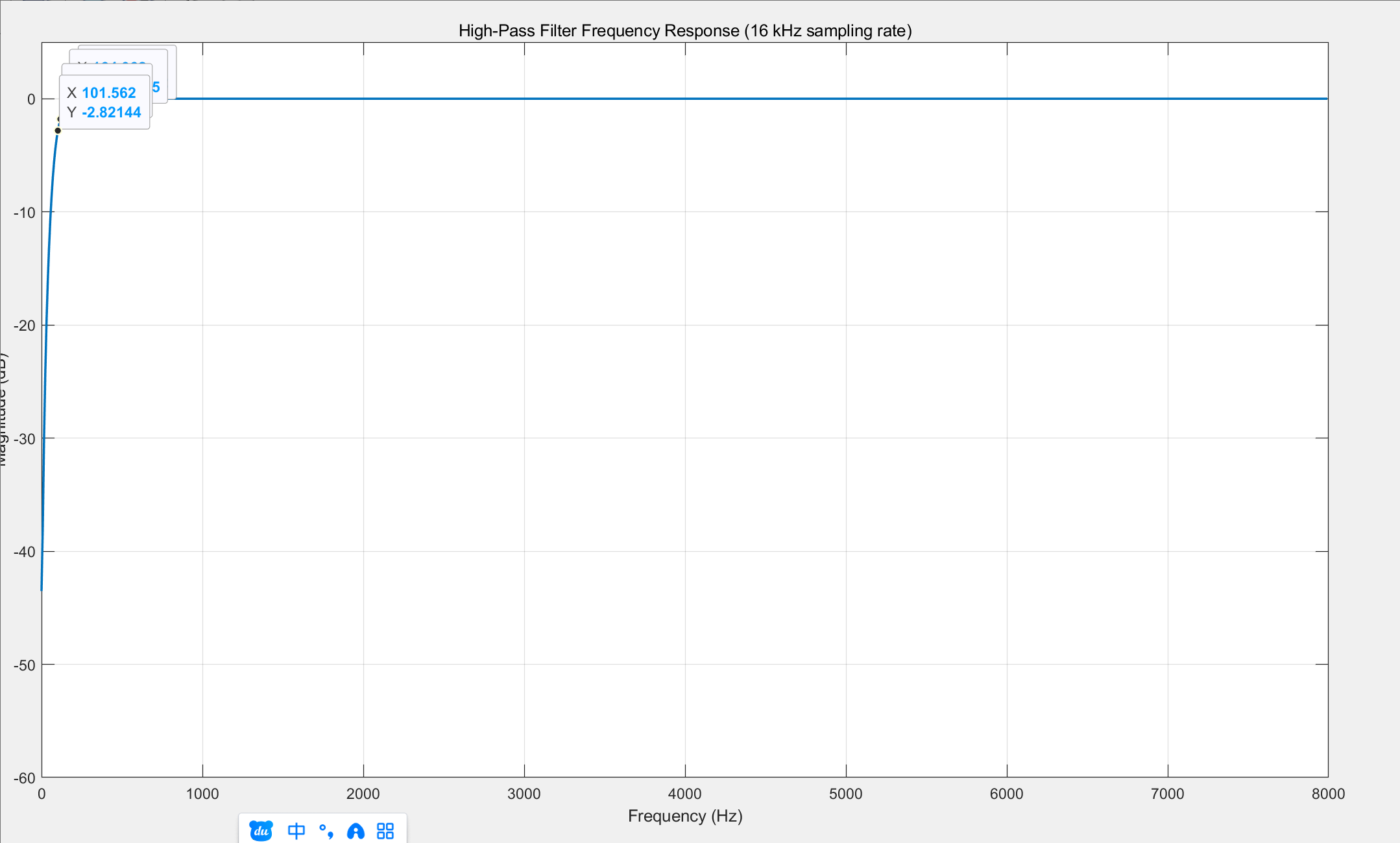
在这里插入图片描述
对应代码如下

% 二阶滤波器系数
b = [0.97261, -1.94523, 0.97261];     % 分子系数（zeros）
a = [1.0, -1.94448, 0.94598];         % 分母系数（poles）

% 使用 freqz 绘制频率响应（默认 512 点）
fs = 16000; % 采样率
[H, f] = freqz(b, a, 1024, fs);

% 绘制幅频响应
figure;
plot(f, 20*log10(abs(H)), 'LineWidth', 1.5);
grid on;
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title('High-Pass Filter Frequency Response (16 kHz sampling rate)');
ylim([-60 5]);

3.滤波过程

1）串联二级IIR滤波器

在进行滤波时，会对于每个IIR滤波器进行串联计算

void CascadedBiQuadFilter::Process(rtc::ArrayView<float> y) {
  for (auto& biquad : biquads_) {
    ApplyBiQuad(y, y, &biquad);
  }
}

2）滤波计算

滤波计算实际就是根据给定的滤波器系数进行反馈回路计算，即：
$y[n]=b_0x[n]+b_1x[n-1]+b_2x[n-2]-a_1y[n-1]-a_2y[n-2]$
代码如下：

void CascadedBiQuadFilter::ApplyBiQuad(rtc::ArrayView<const float> x,
                                       rtc::ArrayView<float> y,
                                       CascadedBiQuadFilter::BiQuad* biquad) {
  RTC_DCHECK_EQ(x.size(), y.size());
  const auto* c_b = biquad->coefficients.b;
  const auto* c_a = biquad->coefficients.a;
  auto* m_x = biquad->x;
  auto* m_y = biquad->y;
  for (size_t k = 0; k < x.size(); ++k) {
    const float tmp = x[k];
    y[k] = c_b[0] * tmp + c_b[1] * m_x[0] + c_b[2] * m_x[1] - c_a[0] * m_y[0] -
           c_a[1] * m_y[1];
    m_x[1] = m_x[0];
    m_x[0] = tmp;
    m_y[1] = m_y[0];
    m_y[0] = y[k];
  }

这段算法整体过程如下：

每个样本：
    x[n] ─┬─► b0 ──┬────┐
          ├─► b1 ─┼────┼──► y[n] = 输出
          ├─► b2 ─┘    ▼
          └─ y[n-1] ─ a0 ──┐
              y[n-2] ─ a1 ─┘

而结构体BiQuad中会保存反馈回路中的输入输出反馈x[2]，y[2]

struct BiQuad {
    explicit BiQuad(const BiQuadCoefficients& coefficients)
        : coefficients(coefficients), x(), y() {}
    explicit BiQuad(const CascadedBiQuadFilter::BiQuadParam& param);
    void Reset();
    BiQuadCoefficients coefficients;
    float x[2];
    float y[2];
  };

总结

webrtc中的高通滤波器是基于二阶IIR滤波器进行设计的，但是对于二阶IIR滤波器不仅仅会在高通滤波器中应用，在以后的webrtc算法介绍中CascadedBiQuadFilter将还会出现。

反正收藏也不会看，不如点个赞吧！

webrtc之高通滤波——HighPassFilter源码及原理分析

文章目录

前言