视频解析:GESP2024年3月三级C++真题讲解
一、单选题
第1题

解析:
答案D,
-5的16位原码:1000 0000 0000 0101
-5的16位反码:1111 1111 1111 1010
-5的16位补码:1111 1111 1111 1011
对应的16进制: F F F B第2题

解析:
答案C,
-2 变 -4等价于:-2*2=-4
整数*2可用(x<<1)表达
E=1110,进行<<1
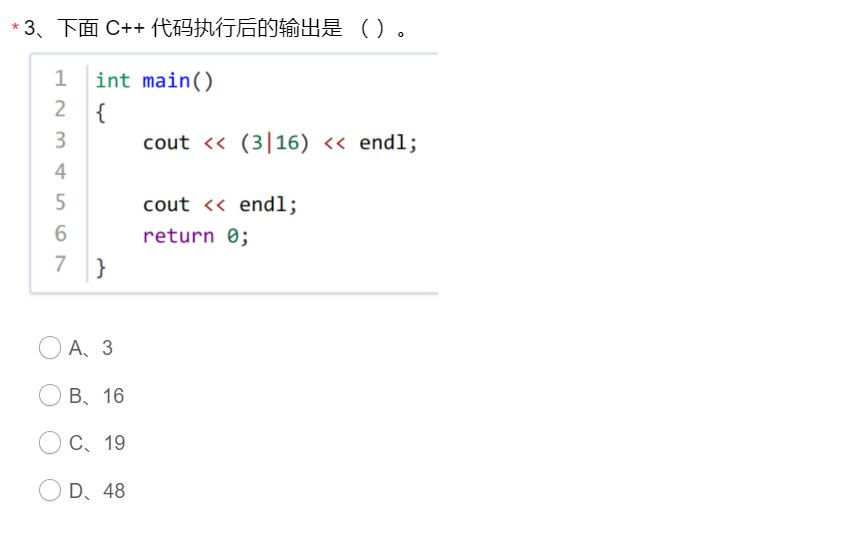
结果为C=1100第3题
解析:
答案C,
3的二进制:0 0011
16的二进制:1 0000
进行 | 运算的结果:1 0011,即19第4题
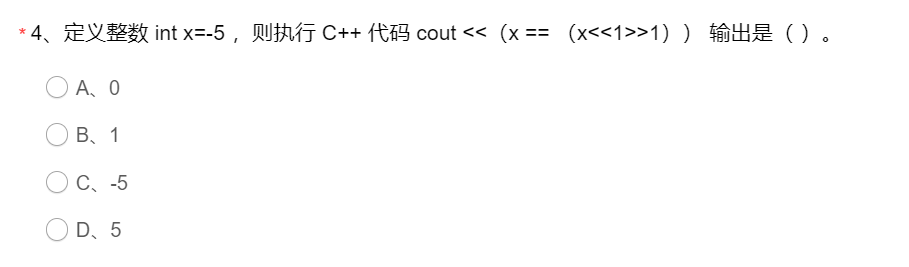
解析:
答案B,
先<<1 再 >>1,-5的补码次高位不受影响,所以值不变
第5题

解析:
答案C,代码是实现字符 '3' , '1' ,'6' 的ASCII值相加,即 51+49+54=154
第6题

解析:
答案C,
if( a[i]%2 && a[i]%3 ) a[i]=0
表达 %2和%3都有余数,就标记为0
即,不能被2和3同时整除,就标记为0
即,能被2或3同时整除,就标记为1
第7题

解析:
答案A,
i为21时退出第一个循环
第二个循环输出的是 a[21-1] = a[20] = 20
第8题

解析:
答案C,
小写转大写,需-32,即 'A' - 'a'
第9题
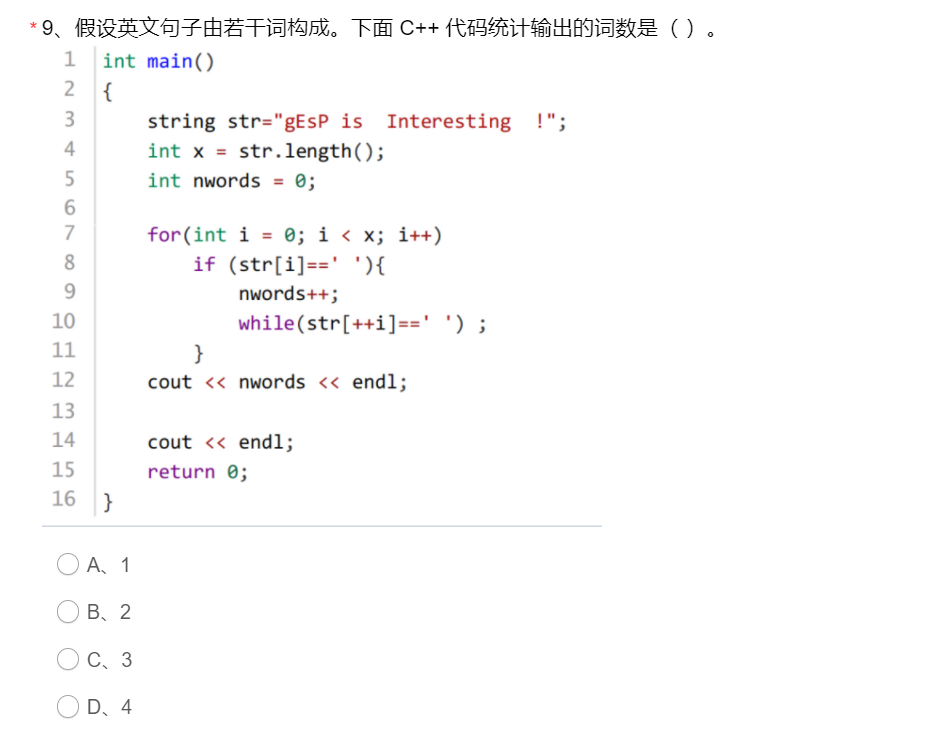
解析:
答案C,
if( str[i] == ' ' ){ //有空格
nwords++; //单词数量+1
while( str[++i] == ' ' ) ; //去除之后连续的空格
}
字符串有3次连续空格,即输出3第10题

解析:
答案C,
全部转为十进制
100(十进制)= 100
075(八进制)= 7*8+5*1 = 61
0x70(十六进制)= 7*16+0*1 = 112 最大
0x60(十六进制)= 6*16+0*1 = 96第11题

解析:
答案D,
1至20,两个连续的值相加,除以3有余数,cnt++
if( ( a[i-1] + a[i-2] ) % 3 )
cnt++;
20+19 = 39 % 3 = 0
19+18 = 37 % 3 = 2
18+17 = 35 % 3 = 2
即按照每次-2的规律
...=33 % 3 =0
...=31 % 3 =2
...=29 % 3 =2
即按照0 2 2的规律,那19对数字中,此规律有12个是2第12题

解析:
答案A,4个字符,即长度为4
第13题

解析:
答案B,
3=0 0011
16=1 0000
所以 3 | 16 = 1 0011 = 19
所以 3 | 16 == 3 + 16第14题

解析:
答案C,鸿蒙、windows、MacOs、Liunx、android都是操作系统
第15题

解析:
答案C,王选发明了 “汉字激光照排系统”
二、判断题
第1题

解析:
答案×,正整数的原码、反码、补码都相同
第2题

解析:
答案×,<<2表示位运算右移两位
第3题

解析:
答案×,穷举的是列举所有情况,判断是否符合条件;累加和只是进行迭代累加
第4题

解析:
答案×,
a的最高位为0,次高位标记为1时,先<<2 再>>2,次高位会变为0
第5题

解析:
答案×,
010是八进制,对应 10 0000(二进制)
<<1结果为,100 0000
第6题

解析:
答案√,
字符:g E s P i s ...
下标:0 1 2 3 4 5 6 ...
第一个‘s’的下标为2第7题

解析:
答案×,
char s[10]; 定义了,大小就不能再做调整了
第8题

解析:
答案√,
循环遍历这个数组,比较找出最小值即可
for(int i=0;i<7;i++){
if(a[i]<minn) minn=a[i];
}第9题

解析:
答案√,路由器就是分配IP,使设备接入网络
第10题

解析:
答案√,
for(int i=1;i<=5;i++){
}
int i=1;
while(i<=5){
i++;
}三、编程题
第1题 [GESP202403 三级] 字母求和
题目描述
小杨同学发明了一种新型密码,对于每一个小写英文字母,该小写字母代表了一个正整数,即该字母在字母顺序中的位置,例如字母 a 代表了正整数 1,字母 b 代表了正整数 2;对于每一个大写英文字母,该大写字母代表了一个负整数,即该字母的 ASCII 码的相反数,例如字母 A 代表了负整数 −65。小杨同学利用这种放缩对一个整数进行了加密并得到了一个由大写字母和小写字母组成的字符串,该字符串中每个字母所代表数字的总和即为加密前的整数,例如 aAc 对应的加密前的整数为 1+(−65)+3=−61。
对于给定的字符串,请你计算出它对应的加密前的整数是多少。
输入格式
第一行一个正整数 n,表示字符串中字母的个数。
第二行一个由大写字母和小写字母的字符串 T,代表加密后得到的字符串。
输出格式
输出一行一个整数,代表加密前的整数。
输入输出样例
输入
3
aAc输出
-61说明/提示
对全部的测试数据,保证 1≤n≤。
答案
#include <iostream>
using namespace std;
int main() {
//1)确定字符数量n
int n;cin>>n;
//2)填充n个字符
int ans=0;
for(int i=1;i<=n;i++){
char chr;cin>>chr;
//3)小写 +序号值
if(chr>='a' && chr<='z'){
ans+= chr-'a'+1;
}else{//4)大写 -ASCII值
ans-=chr;
}
}
//5)输出结果
cout<<ans;
}
第2题 [GESP202403 三级] 完全平方数
题目描述
小杨同学有一个包含 n 个非负整数的序列 A,他想要知道其中有多少对下标组合 ⟨i,j⟩(1≤i<j≤n),使得 Ai+Aj 是完全平方数。
如果 x 是完全平方数,则存在非负整数 y 使得 y×y=x。
输入格式
第一行一个非负整数 n,表示非负整数个数。
第二入行包含 n 个非负整数 A1,A2,…An,表示序列 A 包含的非负整数。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入
5
1 4 3 3 5输出
3说明/提示
对全部的测试数据,保证 1≤n≤1000,0≤Ai≤。
答案
#include <iostream>
#include <math.h>
using namespace std;
int main() {
//1)确定序列数量n
int n;cin>>n;
//2)填充序列
int arr[1010]={};
for(int i=1;i<=n;i++){
cin>>arr[i];
}
//3)枚举所有序列组合
int ans=0;
for(int i=1;i<=n-1;i++){
for(int j=i+1;j<=n;j++){
//4)判断当前组合是否为“完全平方数”
double sqrt_num=sqrt( arr[i]+arr[j] );
if( sqrt_num == int(sqrt_num)){
ans++;
}
}
}
//5)输出结果
cout<<ans;
}