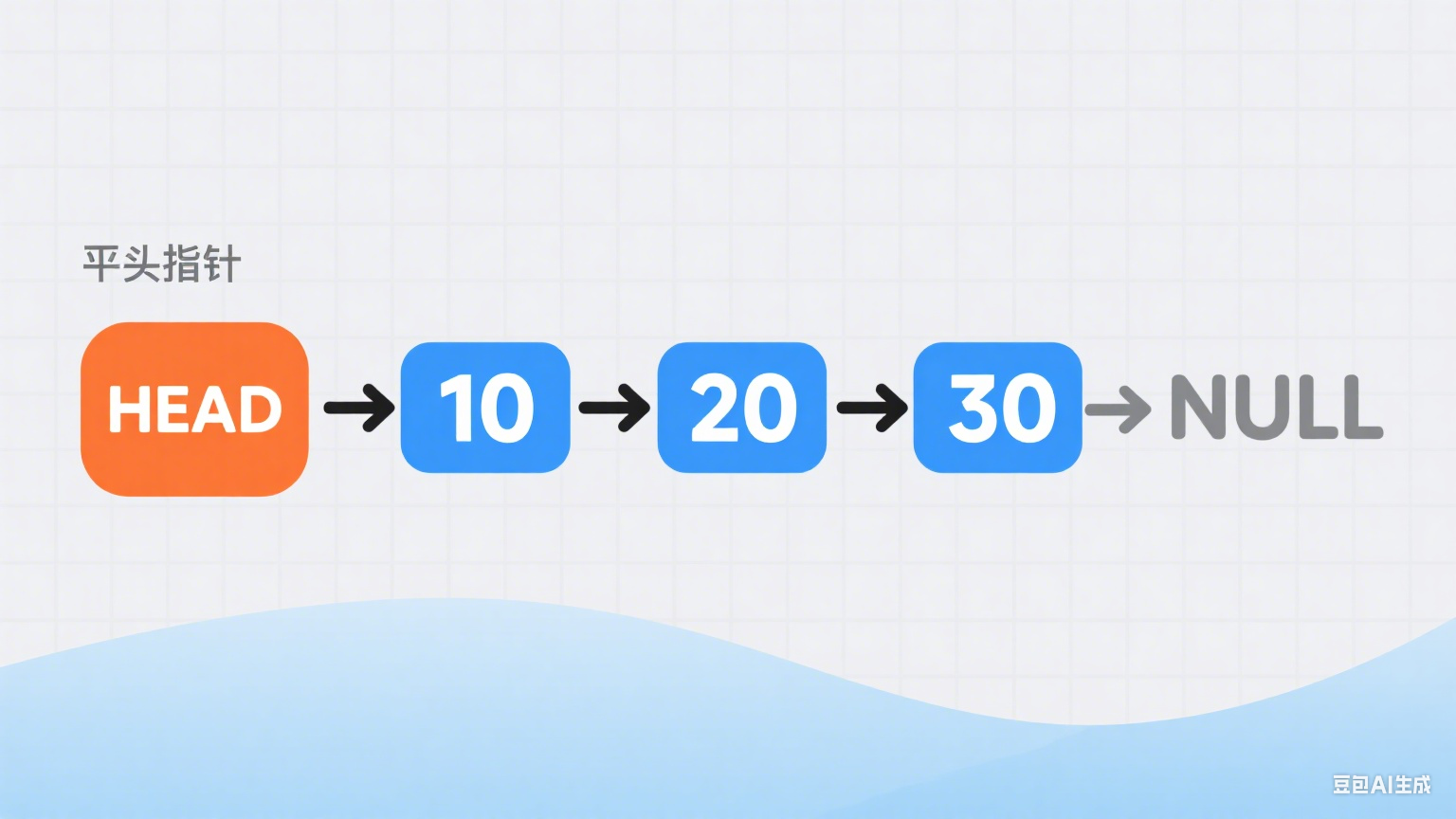
链表
链表算法的核心题目类型是处理指针操作和节点关系,尤其适用于需要频繁插入、删除、或涉及相对顺序/位置关系的场景,而无需随机访问元素。
下面展开详细说明:
一、链表算法的核心题目类型
链表问题看似五花八门,但核心都围绕着“指针”(引用)的操作,主要可以分为以下几类:
基础指针操作与遍历
典型题目:反转链表、寻找链表中点、判断链表是否有环、合并两个有序链表。
核心思想:使用单个指针(如
curr)、双指针(快慢指针、前后指针)或多指针来遍历和操作链表,解决与节点位置、顺序相关的问题。
节点删除与处理
典型题目:删除链表中的节点(给定值或给定节点)、删除链表的倒数第 N 个结点、移除重复元素。
核心思想:维护一个或多个指针来追踪待删除节点的前驱节点(
prev),巧妙地修改next指针的指向以实现删除。虚拟头节点(Dummy Node)是处理头节点可能被删除情况的常用技巧。
链表合并与拆分
典型题目:合并两个有序链表、合并K个升序链表、分隔链表、重排链表。
核心思想:比较节点值,重新组织
next指针的指向,将多个链表合并成一个或将一个链表拆分成多个。常用于排序或重组。
环与相交问题
典型题目:判断链表是否有环、寻找环的入口节点、两个链表的第一个公共节点(相交链表)。
核心思想:快慢指针(Floyd's Cycle-Finding Algorithm) 是解决环问题的经典方法。相交问题则常通过计算链表长度差或巧妙的双指针遍历来找到交汇点。
复杂数据结构的组成部分
典型题目:LFU/LRU缓存机制(链表+哈希表实现)、设计链表、跳表。
核心思想:链表因其高效的插入删除特性,常与其他数据结构(如哈希表)结合,用于实现更高级、功能更复杂的数据结构。
二、什么题目适用于链表?(链表的用武之地)
链表并非万能,但在以下场景中具有数组无法比拟的优势:
频繁的插入和删除操作
场景:当问题的核心操作是在数据序列中频繁地增加或移除元素,而不是查找特定位置的元素时。
原因:链表(尤其是双向链表)的插入和删除操作在已知位置的情况下时间复杂度是 O(1),而数组进行同样操作需要移动后续所有元素,时间复杂度为 O(n)。
例子:实现一个文本编辑器的撤销(Undo)功能,每一步操作都可能被插入或删除。
数据总量不确定或动态变化
场景:无法预知最终会有多少数据,需要一种能够灵活扩展的存储结构。
原因:链表可以动态地申请内存,无需像静态数组一样预先分配固定大小的空间,避免了浪费或溢出的问题。
例子:管理一个不断有新任务加入的任务队列。
需要维护元素的相对顺序或位置关系
场景:问题关注元素之间的前后关系、相邻关系或顺序。
原因:链表通过指针天然地表达了这种“线性”和“顺序”关系,调整顺序只需修改指针,非常高效。
例子:LRU缓存算法需要将最近使用的数据移动到链表头部;反转链表、重排链表等。
反之,如果问题需要频繁地按索引随机访问(get(i)),那么数组(或基于数组的ArrayList)凭借其 O(1) 的访问速度会是更优的选择。
总结:链表是“操作指针的艺术”,其算法题目的本质是考察如何高效地利用指针的指向来解决问题。它最适合处理动态的、需要频繁修改内部结构的数据序列。
三、常用技巧
画图:这样更加直观,形象,便于我们理解!
引入虚拟头节点 --- 这样会不需要考虑很多边界情况,而且方便我们对链表操作,像什么头插/删,尾插/删!
不要吝啬空间,大胆去定义变量(双向循环链表,在中间插入/删除一个元素)
使用快慢双指针可以解决相关的链表题目 --- 判环,找链表中环的入口,找链表中倒数第n个节点
插入操作往往都是先后再前的!
四、常用操作
创建一个新节点 --- new
尾插:
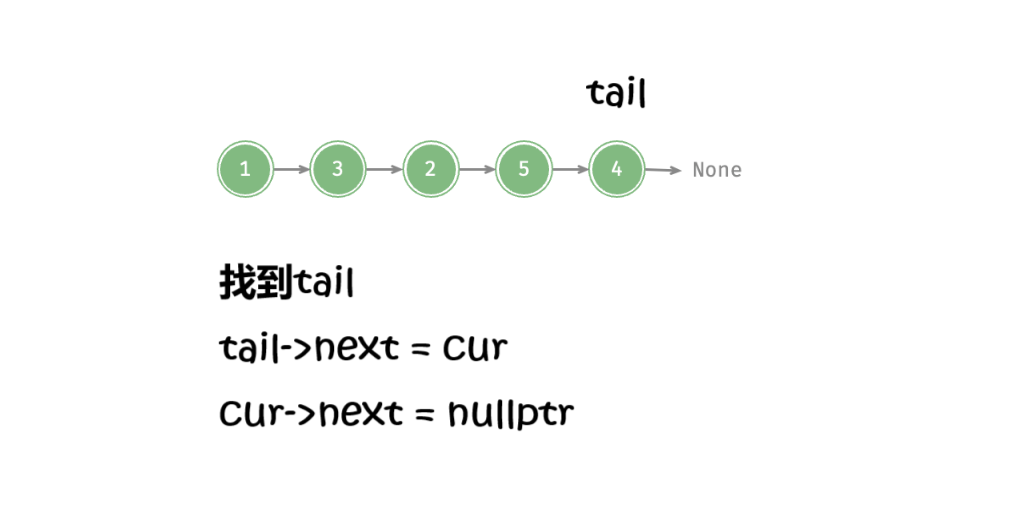
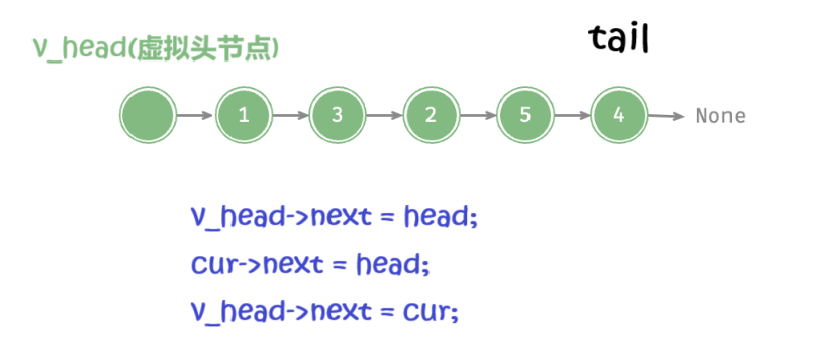
头插:(直接完成逆序链表的题目)
题目练习
2. 两数相加 - 力扣(LeetCode)
解法(模拟):
算法思路:
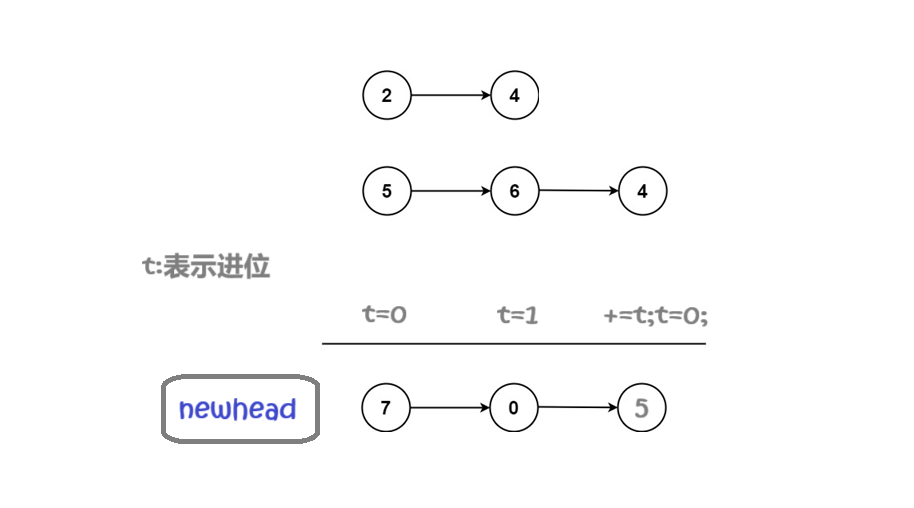
两个链表都是逆序存储数字的,即两个链表的个位数、十位数等都已经对应,可以直接相加。
在相加过程中,我们要注意是否产生进位,产生进位时需要将进位和链表数字一同相加。如果产生进位的位置在链表尾部,即答案位数比原链表位数长一位,还需要再new 一个结点储存最高位。
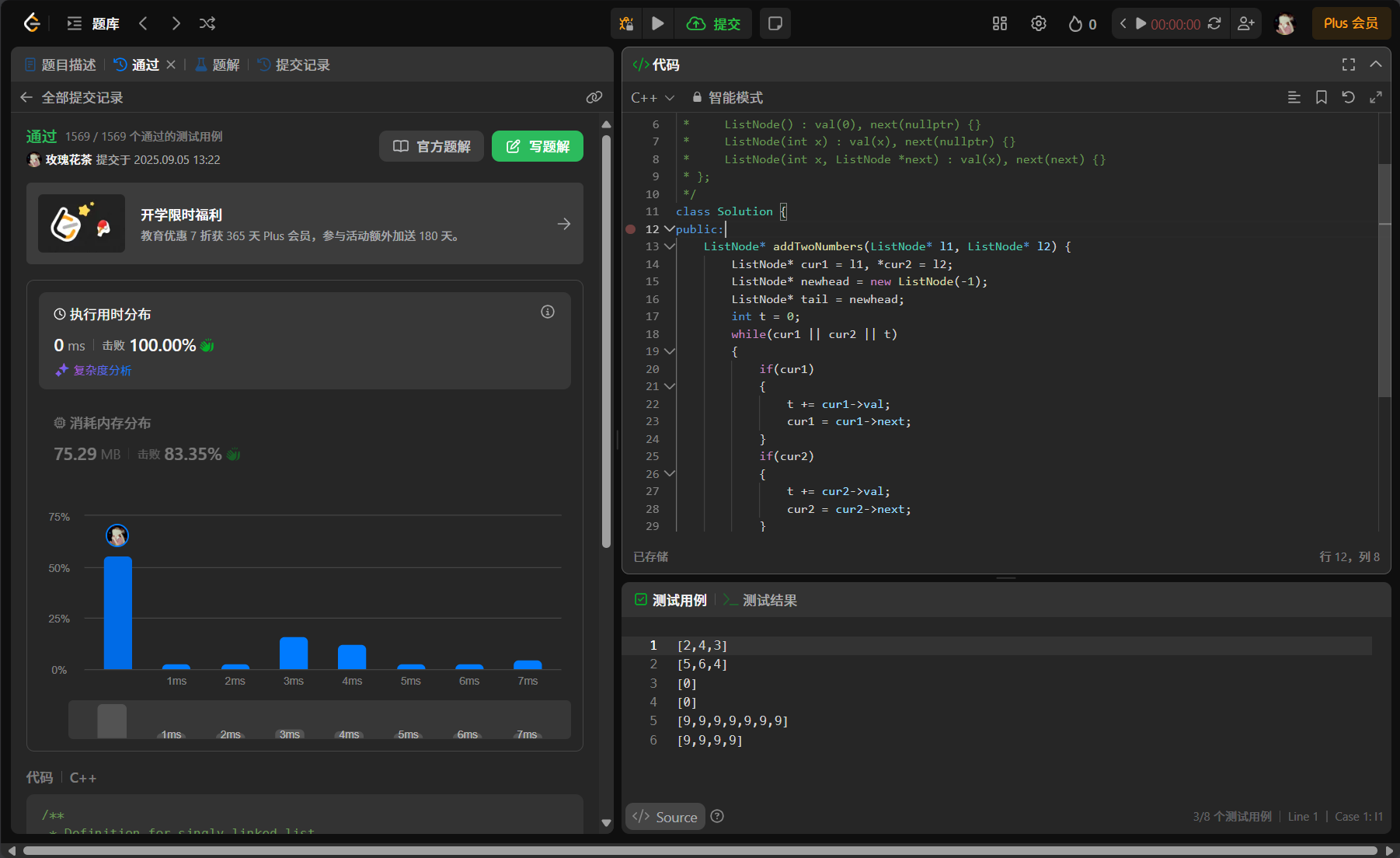
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* cur1 = l1, *cur2 = l2;
ListNode* newhead = new ListNode(-1);
ListNode* tail = newhead;
int t = 0;
while(cur1 || cur2 || t)
{
if(cur1)
{
t += cur1->val;
cur1 = cur1->next;
}
if(cur2)
{
t += cur2->val;
cur2 = cur2->next;
}
tail->next = new ListNode(t % 10);
tail = tail->next;
t /= 10;
}
ListNode* ret = newhead->next;
delete newhead;
return ret;
}
};
24. 两两交换链表中的节点 - 力扣(LeetCode)
解法(模拟):
算法思路:
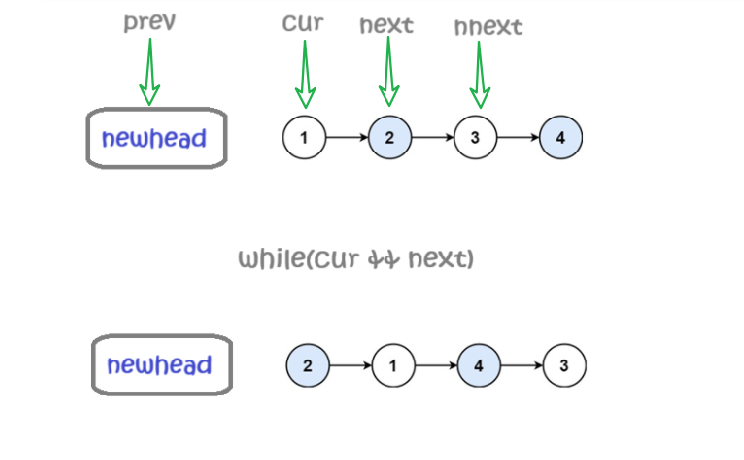
画图画图画图画图,重要的事情说三遍~
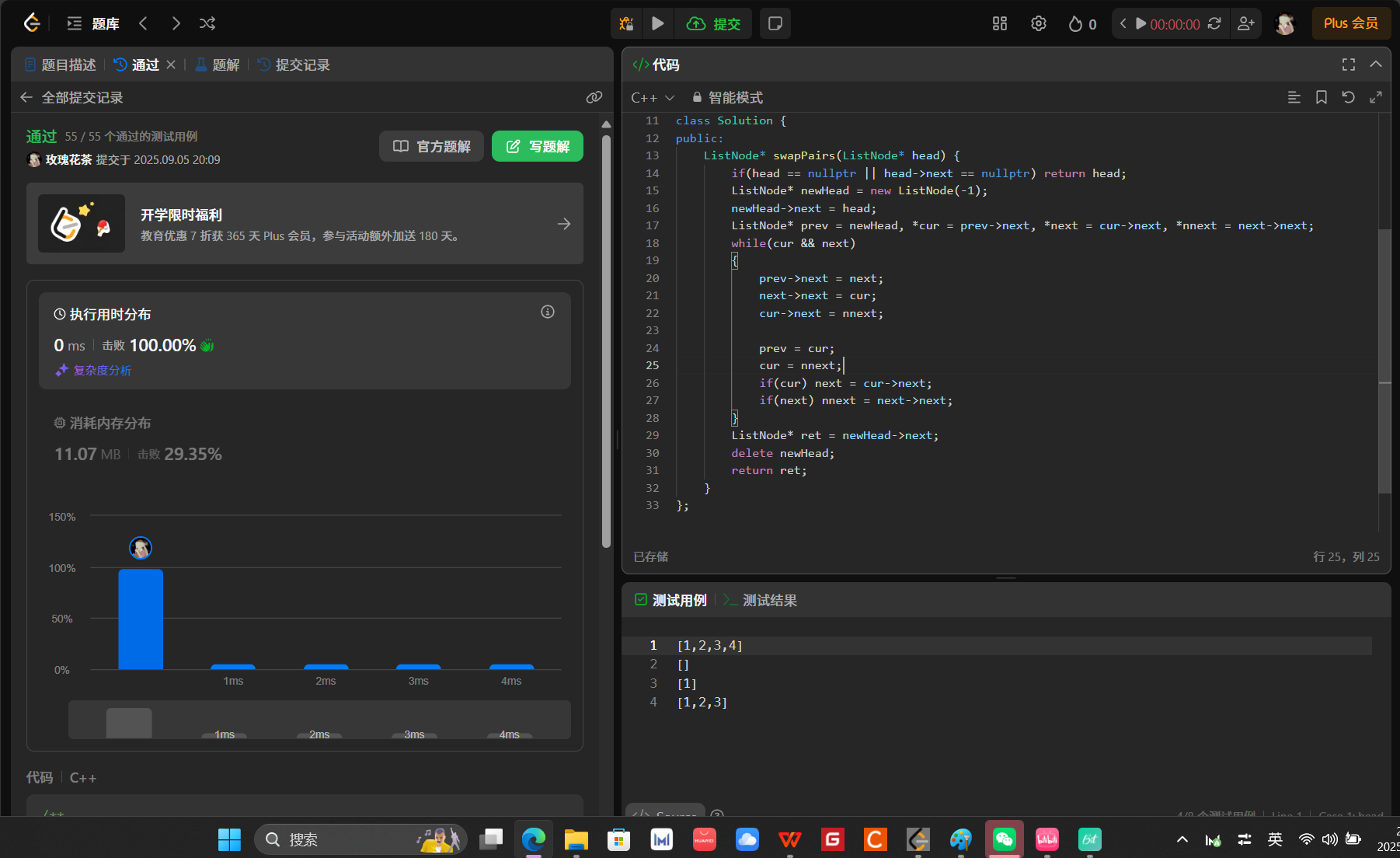
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if(head == nullptr || head->next == nullptr) return head;
ListNode* newHead = new ListNode(-1);
newHead->next = head;
ListNode* prev = newHead, *cur = prev->next, *next = cur->next, *nnext = next->next;
while(cur && next)
{
prev->next = next;
next->next = cur;
cur->next = nnext;
prev = cur;
cur = nnext;
if(cur) next = cur->next;
if(next) nnext = next->next;
}
ListNode* ret = newHead->next;
delete newHead;
return ret;
}
};
143. 重排链表 - 力扣(LeetCode)
解法:
算法思路:
画图画图画图画图,重要的事情说三遍~
找中间节点;
中间部分往后的逆序;
合并两个链表

class Solution {
public:
void reorderList(ListNode* head) {
if(head == nullptr || head->next == nullptr || head->next->next == nullptr) return;
// 找到链表的中间节点
ListNode* slow = head, *fast = head;
while(fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
}
// 使用slow->next来分割,这是可以的,而且可以带来直接分割链表的!
// 逆序
ListNode* head2 = new ListNode(-1);
ListNode* cur = slow->next;
slow->next = nullptr;
while(cur)
{
ListNode* next = cur->next;
cur->next = head2->next;
head2->next = cur;
cur = next;
}
// 合并
ListNode* ret = new ListNode(-1);
ListNode* prev = ret;
ListNode* cur1 = head, *cur2 = head2->next;
delete head2;
while(cur1)
{
prev->next = cur1;
cur1 = cur1->next;
prev = prev->next;
if(cur2)
{
prev->next = cur2;
cur2 = cur2->next;
prev = prev->next;
}
}
ret->next = nullptr;
delete ret;
return;
}
};
23. 合并 K 个升序链表 - 力扣(LeetCode)
解法一(利用堆):
算法思路:
合并两个有序链表是比较简单且做过的,就是用双指针依次比较链表 1、链表 2 未排序的最小元素,选择更小的那一个加入有序的答案链表中。
合并 K 个升序链表时,我们依旧可以选择 K 个链表中,头结点值最小的那一个。那么如何快速的得到头结点最小的是哪一个呢?用堆这个数据结构就好啦~
我们可以把所有的头结点放进一个小根堆中,这样就能快速的找到每次 K 个链表中,最小的元素是哪个。
class Solution {
struct cmp
{
bool operator()(const ListNode* l1, const ListNode* l2)
{
return l1->val > l2->val;
}
};
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
priority_queue<ListNode*, vector<ListNode*>, cmp> heap;
for(auto l : lists)
if(l) heap.push(l);
ListNode* ret = new ListNode(-1);
ListNode* prev = ret;
while(!heap.empty())
{
auto t = heap.top();
heap.pop();
prev->next = t;
prev = t;
if(t->next) heap.push(t->next);
}
ListNode* ans = ret->next;
delete ret;
return ans;
}
};
4. 解法二(递归/分治):
算法思路:
逐一比较时,答案链表越来越长,每个跟它合并的小链表的元素都需要比较很多次才可以成功排序。
比如,我们有 8 个链表,每个链表长为 100。
逐一合并时,我们合并链表的长度分别为(0, 100), (100, 100), (200, 100), (300, 100), (400, 100), (500, 100), (600, 100), (700, 100)。所有链表的总长度共计 3600。
如果尽可能让长度相同的链表进行两两合并呢?这时合并链表的长度分别是(100, 100) x 4, (200, 200) x 2, (400, 400),共计 2400。比上一种的计算量整整少了 1/3。
迭代的做法代码细节会稍多一些,这里给出递归的实现,代码相对简洁,不易写错。
算法流程:
特判,如果题目给出空链表,无需合并,直接返回;
返回递归结果。
递归函数设计:
递归出口:如果当前要合并的链表编号范围左右值相等,无需合并,直接返回当前链表;
应用二分思想,等额划分左右两段需要合并的链表,使这两段合并后的长度尽可能相等;
对左右两段分别递归,合并[l, r]范围内的链表;
再调用 mergeTwoLists 函数进行合并(就是合并两个有序链表)
class Solution {
public:
ListNode* mergeToList(ListNode *l1, ListNode *l2)
{
if(l1 == nullptr) return l2;
if(l2 == nullptr) return l1;
ListNode head;
ListNode* cur1 = l1;
ListNode* cur2 = l2;
ListNode* prev = &head;
head.next = nullptr;
while(cur1 && cur2)
{
if(cur1->val <= cur2->val)
{
prev = prev->next = cur1;
cur1 = cur1->next;
}
else
{
prev = prev->next = cur2;
cur2 = cur2->next;
}
}
if(cur1) prev->next = cur1;
if(cur2) prev->next = cur2;
return head.next;
}
ListNode* mergeSort(vector<ListNode*>& lists, int l, int r)
{
if(l > r) return nullptr;
if(l == r) return lists[l];
int mid = ((r - l) >> 1) + l;
ListNode *l1 = mergeSort(lists, l, mid);
ListNode *l2 = mergeSort(lists, mid + 1, r);
return mergeToList(l1, l2);
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
return mergeSort(lists, 0, lists.size() - 1);
}
};
25. K 个一组翻转链表 - 力扣(LeetCode)
解法(模拟):
算法思路:
本题的目标非常清晰易懂,不涉及复杂的算法,只是实现过程中需要考虑的细节比较多。
我们可以把链表按 K 个为一组进行分组,组内进行反转,并且记录反转后的头尾结点,使其可以和前、后连接起来。思路比较简单,但是实现起来是比较复杂的。
我们可以先求出一共需要逆序多少组(假设逆序 n 组),然后重复 n 次长度为 k 的链表的逆序即可。
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
int n = 0;
ListNode* cur = head;
while(cur)
{
cur = cur->next;
n++;
}
n /= k;
ListNode* newhead = new ListNode(-1);
ListNode* prev = newhead;
cur = head;
for(int i = 0 ;i < n; ++i)
{
ListNode* tmp = cur;
for(int j = 0; j < k; ++j)
{
ListNode* next = cur->next;
cur->next = prev->next;
prev->next = cur;
cur = next;
}
prev = tmp;
}
prev->next = cur;
cur = newhead->next;
delete newhead;
return cur;
}
};