题目1:快乐数
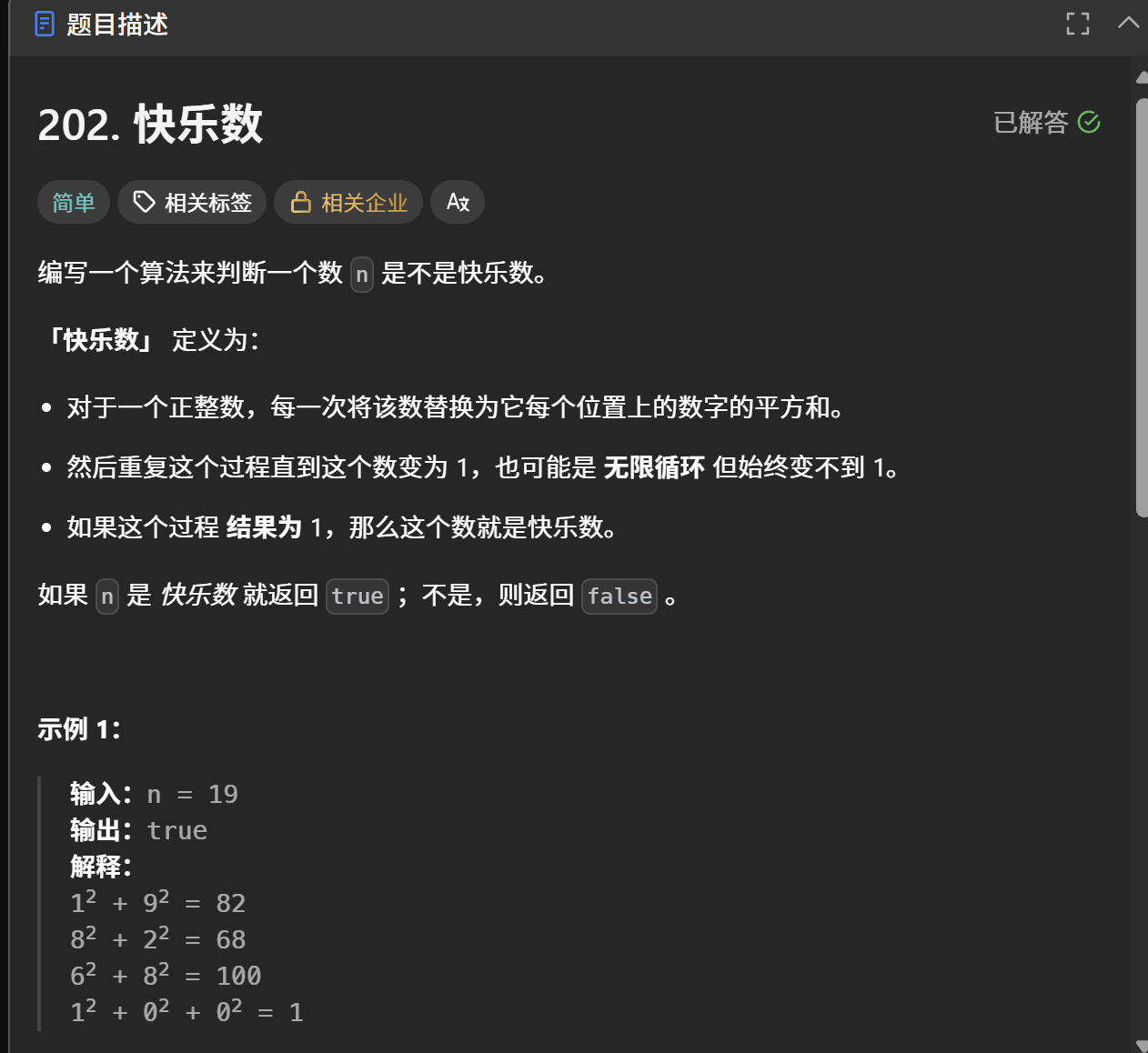
我们先来结合实例看一下判断快乐数的整个过程:
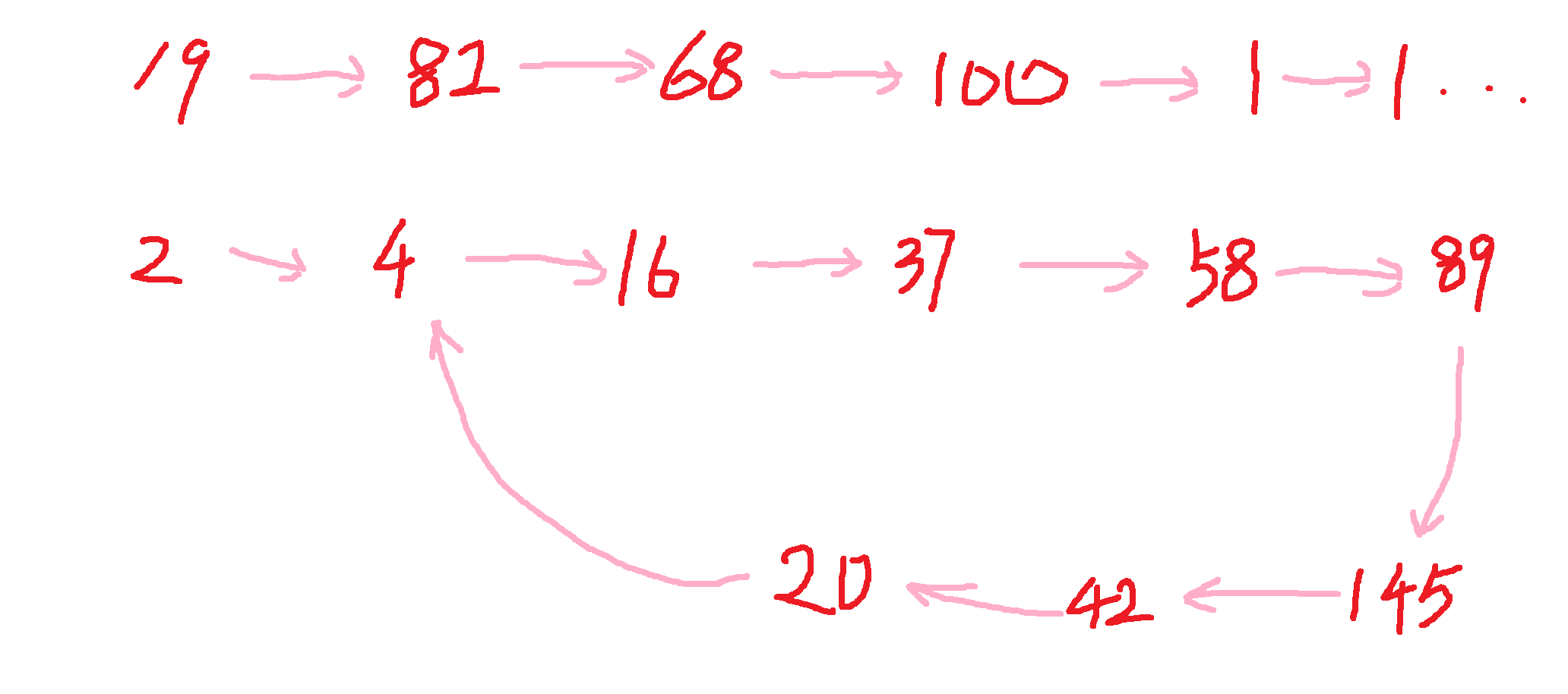
结合题目可以知道,如果一个数是快乐数,那么这个数最终就会变成1,如果一个数不是快乐数,那么变化序列最终就会陷入循环。想一下,如果题目没有告诉我们“如果一个数不是快乐数,最后会陷入死循环”这句话,我们应该如何来证明这个观点?
这里就要用到小学学过的“鸽巢原理”(抽屉原理)来进行简单的证明。
鸽巢原理:如果一共有n个鸽巢,有n+1只鸽子,那么一定存在至少一个鸽巢,这个鸽巢里面的格子数大于1.
我们知道n是一个整型类型而且n>0,那么n的取值范围就在1~2^31-1,而2^31-1=2147483647,这个数一定小于9999999999,如果非快乐数的变化不是循环的,那么总有一次会变成最大的那一个数2147483647,而这个数小于9999999999,在经过题目所说的变化以后,一定会变成小于(9^2)*10=810的数x,所以这个数经过相应的又会进入新一轮的循环,所以我们一开始的假设(即非快乐数的变化不是循环的)是错误的,所以一个非快乐数,他经过相应的变化以后会进入一个循环的序列。
结合上图和解释,我们可以将序列的变化抽象为下面的图:

如果看过数据结构之链表篇的兄弟对这一张图一定很熟悉,这就是我们之前做的带环的链表的那一道题(这道题可以参考:https://blog.csdn.net/pusue_the_sun/article/details/150438603?fromshare=blogdetail&sharetype=blogdetail&sharerId=150438603&sharerefer=PC&sharesource=pusue_the_sun&sharefrom=from_link)
在那一道题中我们所使用的思路是前后指针,同理这一道题我们也可以使用前后指针的思想。
我们先定义一个快指针和慢指针,初始时慢指针的值就等于n,而快指针的值就等于n经过一次变化以后所得到的值。然后每次让慢指针经历一次变化,快指针经过两次变化,最后快慢指针一定都会进入成环的那一部分,那么最终快慢指针就一定会相遇,即它们两个的值一定会相同(这个结论的分析过程见带环的链表那一道题),接下来我们只需判断当它们两的值相同时,slow的值是1还是其他值,如果是1,那么就代表n是快乐数,反之就不是快乐数。
//快慢指针
//将一个数替换为他们个位置上的数字的平方和
int Func(int n)
{
int m=n;
int sum=0;
while(m)
{
int x=m%10;
sum+=x*x;
m/=10;
}
return sum;
}
bool isHappy(int n)
{
int slow=n;
int fast=Func(n);
while(fast!=slow)
{
slow=Func(slow);
fast=Func(fast);
fast=Func(fast);
}
return slow==1;
}题目2:盛最多水的容器
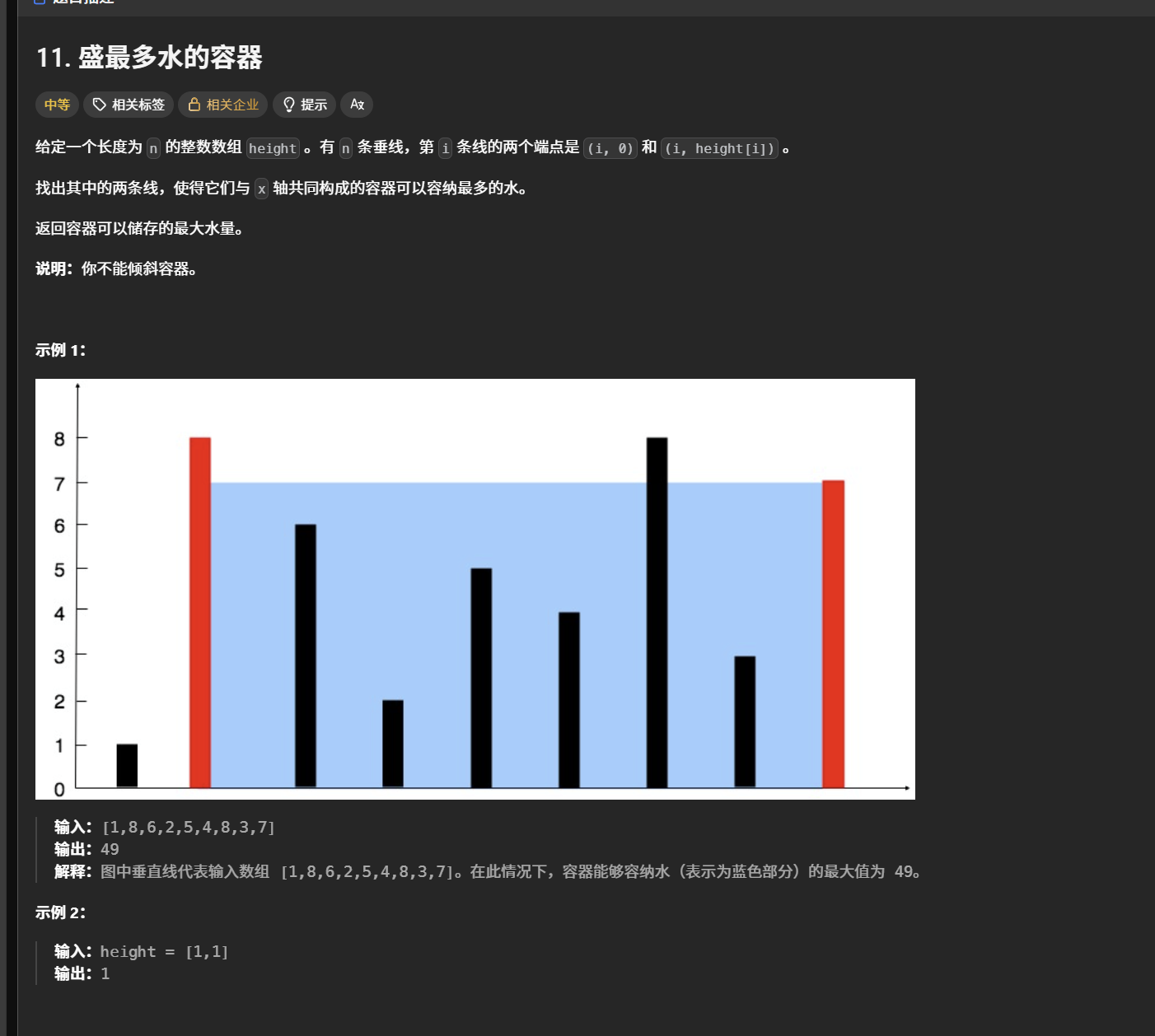
方法一:暴力求解。这道题我们当然可以使用双层循环求任意两个区间中容器的体积,然后比较得到最大的容积。但是,这个思路虽然好想,时间复杂度却太高了,无法通过题解。
方法二:双指针法。我们知道,对于任意一个区间,容器的体积是由宽度和高度两部分决定的,根据木桶效应,一个区间容器的高度有较小的高度决定。假设我们一开始将宽度拉到最大,即包含整个区间(区间范围是 [0,heightsize-1] ),算出这一部分的体积,然后再缩小宽度,依次去计算对应区间的体积并比较,然后就可以得到最大体积。我们应该如何缩小宽度才能达到找到最大体积的目的呢?我们知道,体积是由宽度和高度共同决定的,当我们缩小宽度时,如果还想让体积变大,就一定要让高度变大,所以对于区间的两个端点,我们需要舍弃对应高度较小的那一个端点来缩小宽度。
结合上述思路我们来整理出这道题的算法步骤:
1.定义两个指针right和left分别指向数组的最右边和最左边
2.计算left到right区间的容积
3.缩小区间范围,如果left对应的高度小于right对应的高度,就让left++;反之就让right--
4.通过比较更新最大容积
现在我们就可以来写代码啦:
int maxArea(int* height, int heightSize)
{
int max=0;
int left=0,right=heightSize-1;
while(left<right)
{
int h=height[left]<height[right]?height[left]:height[right];
int v=h*(right-left);
if(height[left]<height[right])
{
left++;
}else{
right--;
}
if(v>max)
{
max=v;
}
}
return max;
}小结:这一小节我们主要通过两个算法题对应用双指针的解题思路进行了讲解。小伙伴们一定要自己在草稿纸或者电脑上多画一下图以深入理解算法的思想。
欢迎小伙伴们在评论区提出问题和讨论!!!