


专栏:算法的魔法世界
个人主页:手握风云
目录
一、例题讲解
1.1. 电话号码的字母组合

仅包含数字2—9的字符串,返回该数字字符串能表示的所有字母组合,组合顺序可任意。
我们先利用字符串数组映射出数字和字母之间的关系。然后画出决策树,我们只需对决策树进行深度优先遍历,收集叶子节点的值。递归方法的设计,我们需要递归处理电话号码对应的字符串以及字符串的下标。当把字符串的最后一个字符添加进路径中的字符串后,回溯。递归的出口,遍历完字符串的最后一个位置。
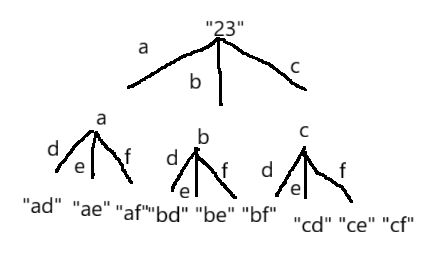
完整代码实现:
class Solution {
public String[] hash = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public StringBuffer path; // 储存当前路径的字符串
public List<String> ret; // 储存最终结果
public List<String> letterCombinations(String digits) {
path = new StringBuffer();
ret = new ArrayList<>();
// 字符串为空,直接返回空列表
if (digits.length() == 0) {
return ret;
}
dfs(digits, 0); // 深搜
return ret;
}
private void dfs(String digits, int pos) {
// 到达字符串末尾,递归出口
if (pos == digits.length()) {
ret.add(path.toString());
return;
}
String index = hash[digits.charAt(pos) - '0'];
for (int i = 0; i < index.length(); i++) {
path.append(index.charAt(i));
// 递归处理下一个数字
dfs(digits, pos + 1);
// 回溯
path.deleteCharAt(path.length() - 1);
}
}
}1.2. 括号生成

返回一个字符串列表,包含所有可能且有效的括号组合;括号组合需满足 “有效”—— 即左括号与右括号数量均为n,且任意前缀中左括号数量不小于右括号数量。
通过下图的决策树,我们很容易发现剪枝的策略:当左括号数量>=m时;右括号数量大于左括号数量时。递归方法不用传参数,只需要对决策树往下递归并添加左括号或者右括号即可。当遍历到叶子节点时,同时这里也是递归出口,回溯时,只需把字符串的最后一个字符删掉即可。
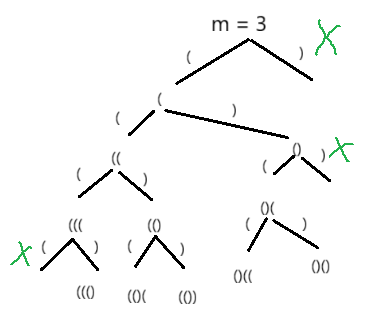
完整代码实现:
class Solution {
// 左括号和右括号数量
int left, right, m;
StringBuffer path;
List<String> ret;
public List<String> generateParenthesis(int n) {
m = n;
path = new StringBuffer();
ret = new ArrayList<>();
dfs();
return ret;
}
public void dfs() {
// 当右括号数量等于m时,表示已经完成了一个合法的组合
if (right == m) {
ret.add(path.toString());
return;
}
// 如果左括号数量小于m,添加左括号
if (left < m) {
path.append('(');
left++;
dfs();
// 回溯
path.deleteCharAt(path.length() - 1);
left--;
}
// 如果右括号数量小于左括号数量,可以添加右括号
if (right < left) {
path.append(')');
right++;
dfs();
// 回溯
path.deleteCharAt(path.length() - 1);
right--;
}
}
}1.3. 组合

给定两个整数n和k,返回范围[1, n]中所有由k个不同数组成的组合,组合内元素顺序不影响。
通过下图的决策树可以看出:当选到重复数字时;因为返回顺序可任意,所以123、213是同一种情况,可以剪枝。这里我们不需要全局变量进行剪枝,当我们选出第一个数字i时,只需要枚举[i, n]之间的数字即可。递归函数传入一个起始位置start,当收集到的结果的长度=k时,就是到达了叶子结点,此时将叶子结点的结果添加到结果集中。
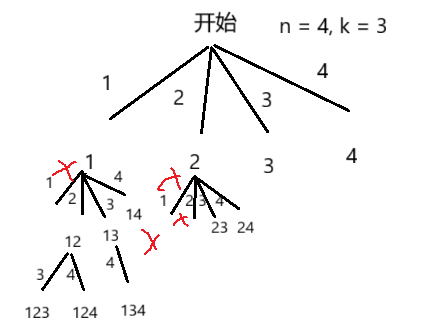
class Solution {
int m, j;
List<Integer> path;
List<List<Integer>> ret;
public List<List<Integer>> combine(int n, int k) {
// 初始化
m = n;
j = k;
path = new ArrayList<>();
ret = new ArrayList<>();
dfs(1);
return ret;
}
private void dfs(int start) {
// 如果当前路径长度等于j,将目前路径添加到结果集中
if (path.size() == j) {
ret.add(new ArrayList<>(path));
return;
}
// 遍历所有可能的数字
for (int i = start; i <= m; i++) {
path.add(i);
// 递归处理下一个元素
dfs(i + 1);
// 回溯
path.remove(path.size() - 1);
}
}
}1.4. 目标和

给定一个非负整数数组nums,以及一个整target;给nums中的每个整数前分别添加 '+'或'-',再将所有整数串联,构造出一个表达式。统计并返回运算结果等于target的不同表达式的数目。
当我们把决策树画出来之后,这道题起始就是二叉树的深搜,就是寻找叶子节点的值是否等于target。
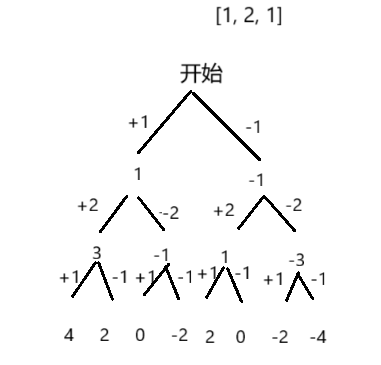
class Solution {
int path, ret, aim;
public int findTargetSumWays(int[] nums, int target) {
aim = target;
dfs(nums, 0);
return ret;
}
private void dfs(int[] nums, int pos) {
// 处理完数组所有元素
if (pos == nums.length) {
// 如果当前路径和等于目标值,则计数加一
if (path == aim) {
ret++;
}
return;
}
// 加上当前数字
path += nums[pos];
// 递归处理下一个数字
dfs(nums, pos + 1);
// 回溯
path -= nums[pos];
// 减去当前数字
path -= nums[pos];
// 递归处理下一个数字
dfs(nums, pos + 1);
// 回溯
path += nums[pos];
}
}