【Leetcode hot 100】543.二叉树的直径

问题链接

543.二叉树的直径

问题描述

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

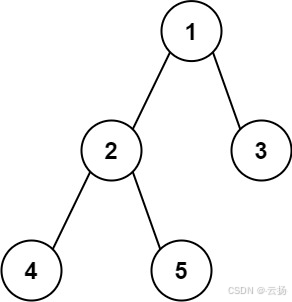
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 [1, 104] 内
• -100 <= Node.val <= 100

问题解答

解题思路

1. 核心观察：二叉树的直径 = 某个节点的左子树深度 + 右子树深度（路径以该节点为中心，左右延伸）。
2. 深度优先搜索（DFS）：通过 DFS 计算每个节点的子树深度时，同步记录“当前节点的左右子树深度之和”，并更新全局最大直径。
3. 边界处理：若树为空（根节点为 null），直径为 0；若树只有一个节点，直径也为 0（无边）。

Java 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int diameterOfBinaryTree(TreeNode root) {
        // 用数组存储最大直径（Java 中基本类型无法在递归中修改，数组是引用类型）
        int[] maxDiameter = {0};
        // 调用 DFS 计算深度，同时更新最大直径
        calculateDepth(root, maxDiameter);
        return maxDiameter[0];
    }

    /**
     * 计算当前节点的子树深度，并同步更新最大直径
     * @param node 当前节点
     * @param maxDiameter 存储最大直径的数组（引用传递）
     * @return 当前节点的子树深度（以当前节点为根的树的深度）
     */
    private int calculateDepth(TreeNode node, int[] maxDiameter) {
        // 递归终止条件：空节点深度为 0
        if (node == null) {
            return 0;
        }

        // 递归计算左子树深度
        int leftDepth = calculateDepth(node.left, maxDiameter);
        // 递归计算右子树深度
        int rightDepth = calculateDepth(node.right, maxDiameter);

        // 更新最大直径：当前节点的左右子树深度之和可能是新的最大值
        maxDiameter[0] = Math.max(maxDiameter[0], leftDepth + rightDepth);

        // 返回当前节点的子树深度：1（当前节点自身） + 左右子树的最大深度
        return 1 + Math.max(leftDepth, rightDepth);
    }
}

代码解释

1. 递归函数 calculateDepth：

   • 作用：既计算当前节点的子树深度，又在计算过程中更新全局最大直径。
   • 终止条件：空节点的深度为 0（node == null 时返回 0）。
   • 核心逻辑：
     • 先递归计算左、右子树的深度（leftDepth 和 rightDepth）。
     • 用 leftDepth + rightDepth 计算当前节点的“左右子树深度之和”，并与 maxDiameter[0] 比较，更新最大直径。
     • 返回当前节点的子树深度：1 + Math.max(leftDepth, rightDepth)（1 代表当前节点自身，加上左右子树的最大深度）。

2. 为什么用数组存储 maxDiameter：
   Java 是值传递，若用 int 基本类型，递归函数中修改的值无法传递到外部。用数组（长度为 1）存储，数组是引用类型，递归中修改数组元素会直接影响外部。

复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每个节点仅被遍历一次（DFS 递归一次）。
• 空间复杂度：O(h)，其中 h 是二叉树的高度。递归调用栈的深度等于树的高度（平衡树 h = log n，最坏情况（斜树）h = n）。

示例验证

• 示例 1：输入 root = [1,2,3,4,5]

  • 节点 2 的左深度 = 1（节点 4），右深度 = 1（节点 5），和为 2。
  • 节点 1 的左深度 = 2（节点 2 的子树深度），右深度 = 1（节点 3），和为 3 → 最大直径更新为 3。
  • 最终返回 3，与示例输出一致。

• 示例 2：输入 root = [1,2]

  • 节点 1 的左深度 = 1（节点 2），右深度 = 0，和为 1 → 最大直径为 1。
  • 最终返回 1，与示例输出一致。