作者前言：本章内容是作者阅读《机器学习》（周志华）（网友戏称“西瓜书”，因为本书作者从第一章开始便通过如何辨别好的西瓜的例子来剖析机器学习的实质以及书的封面是西瓜）及相关资料写的。笔者在写此博客前，也看到了网上发布了大量相关此书的读书笔记，但翻来看去发现存在公式放的较多、大量拍摄书上的内容照片直接贴图等情况，不太适合新手阅读。故，作者写下此篇博客。笔者尽可能简化公式或者不放公式，读者在阅读。过程中不要过于纠结看懂里面的数学公式，只需搞懂里面各种的作用，内在大致的缘由即可。
本章含有大量的数学公式和推导过程，作者极力对其简化，读者不要强求弄懂里面的推导和数学公式，只需大概理解其意即可。毕竟，我们目前只是学习它内在的大致原理，里面的数学公式需要较强的数学基础，读者可等后续有了之后才来进行推导。
PS：本章是书上的第六章，全书共有11种模型的讲解，含有线性模型、决策树、神经网络、支持向量机（SVM）、贝叶斯分类器、集成学习、聚类、半监督学习、概率图模型、规则学习、强化学习。下一章将更新聚类!!! 请持续关注作者!!! 由于贝叶斯分类器中有大量概率问题，作者目前都还没有搞懂里面的东西，请等待作者的后续发布！！！
目录
一、间隔与支持向量
分类学习（这里讨论的是简单的二分类情形）最基本的想法就是基于训练集D在样本空间找到一个划分超平面，将不同类别的样本分开。但能将训练样本分开的划分超平面可能有很多，如下图所示，应该找哪一个呢？
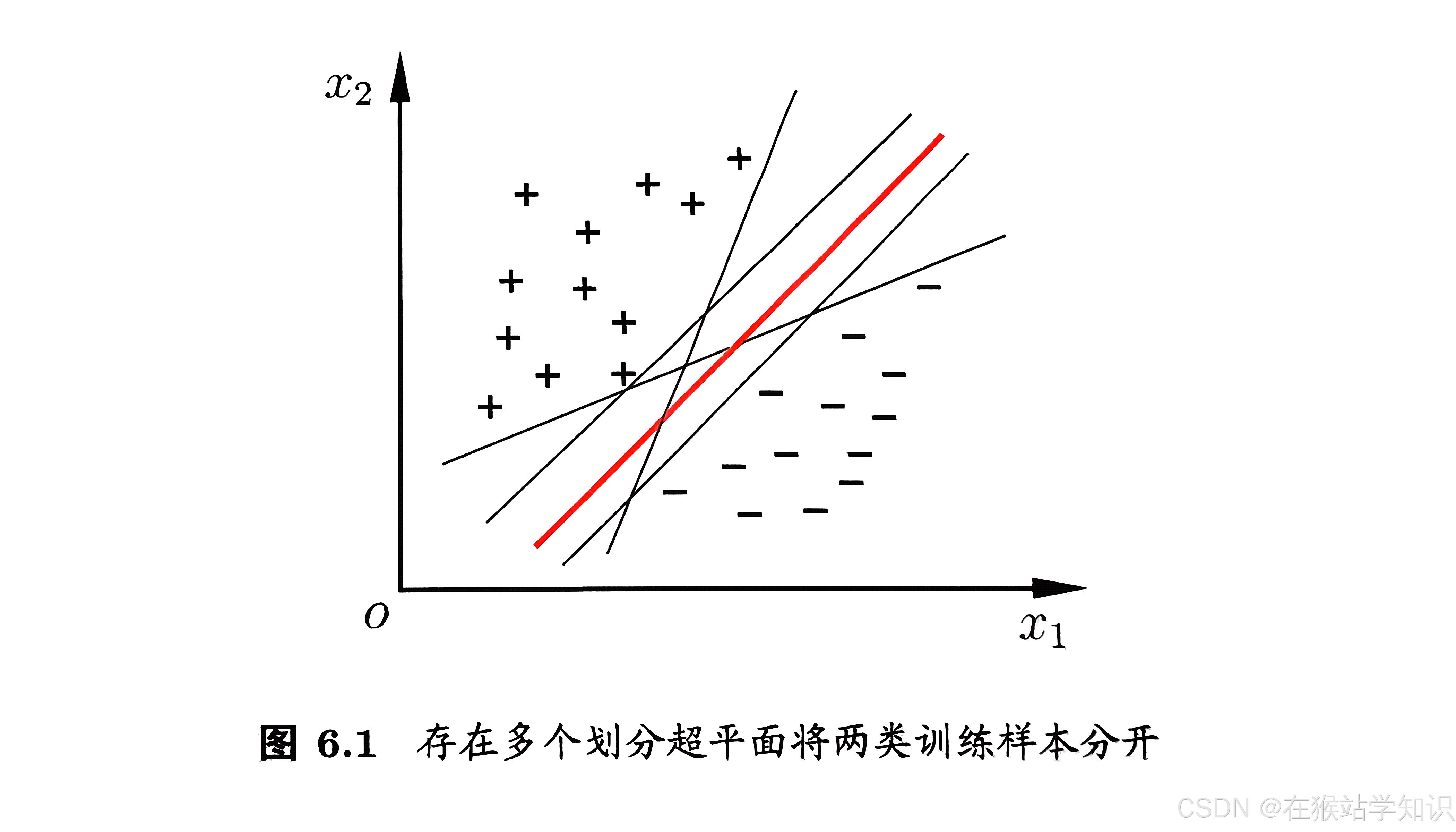
直观上看，应找位于两类样本“正中间”的划分超平面（上图的红色线条），因为它对样本局部扰动的“容忍”性最好。换言之，这个划分超平面所产生的分类结果是最鲁棒性的，对未见示例的泛化能力最强。在样本空间，划分超平面可通过下面的线性方程来描述：
其中为法向量，决定了超平面的方向；b为位移项，决定了超平面与原点之间的距离。显然，划分超平面被w和b确定，下面将其记为(w,b)。样本空间中任意点x到超平面(w,b)的距离可写为：
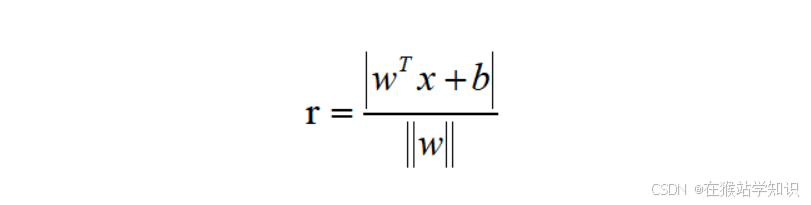
假设超平面(w,b)能将训练样本正确分类，即对于，若
,则有
；若
,则有。令：
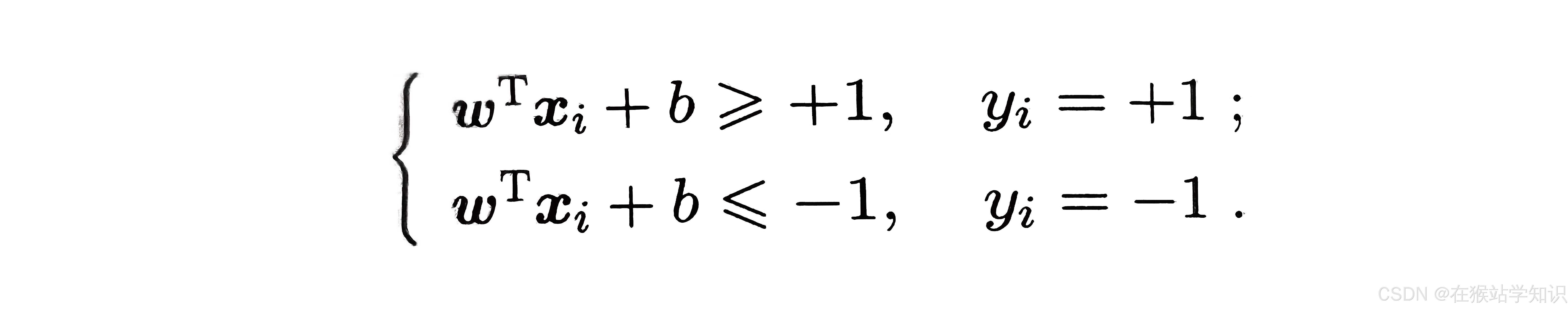
如下图所示，距离超平面最近的这几个训练样本点使上式的等号成立，它们被称为“支持向量”，两个异类支持向量到超平面的距离之和为：
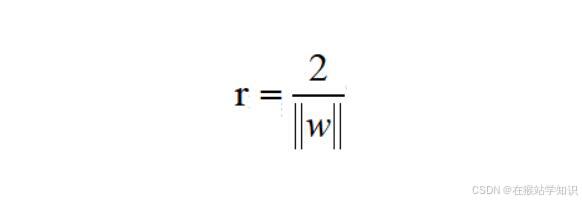
它被称为“间隔”。
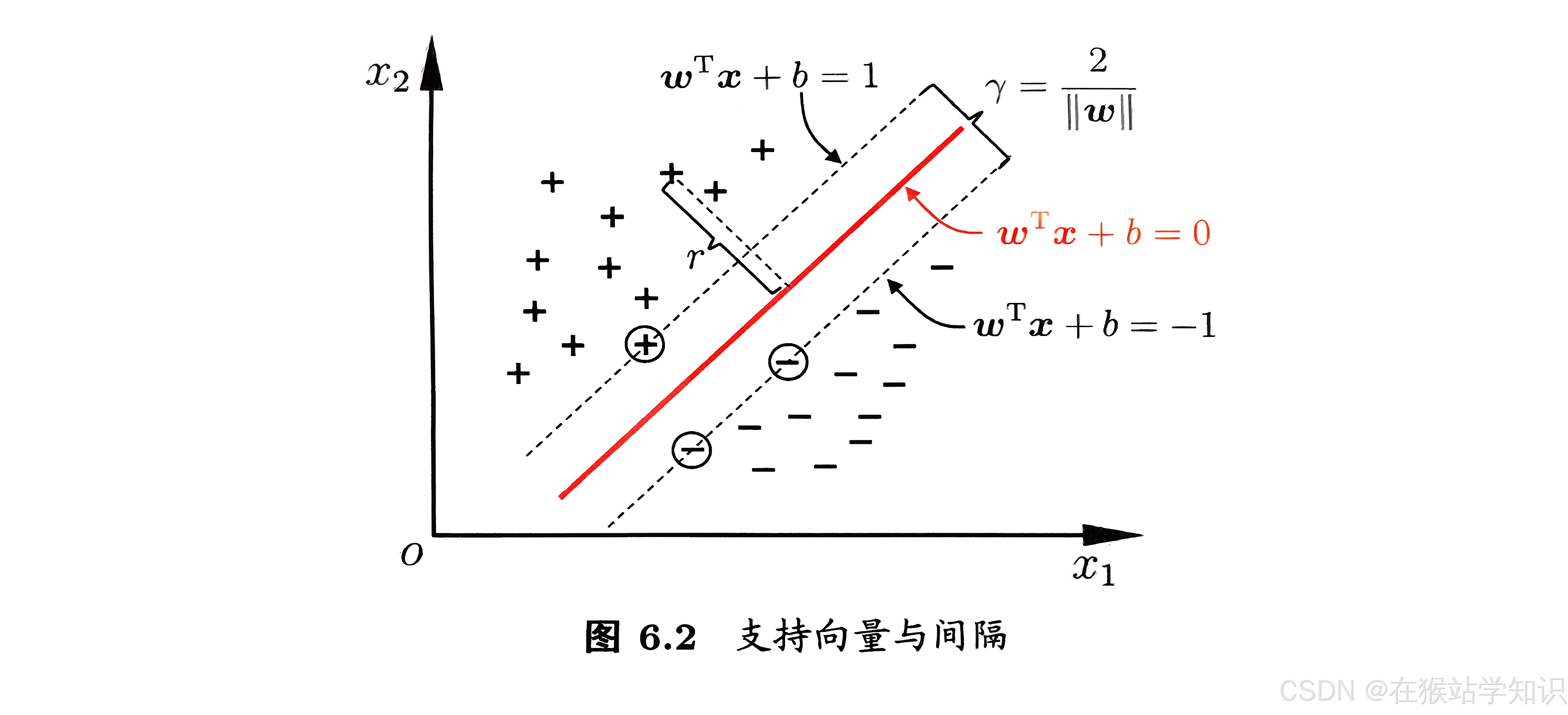
欲找到具有“最大间隔”的划分超平面，也就是要找能满足上式的约束参数的w和b，使得r最大。即：
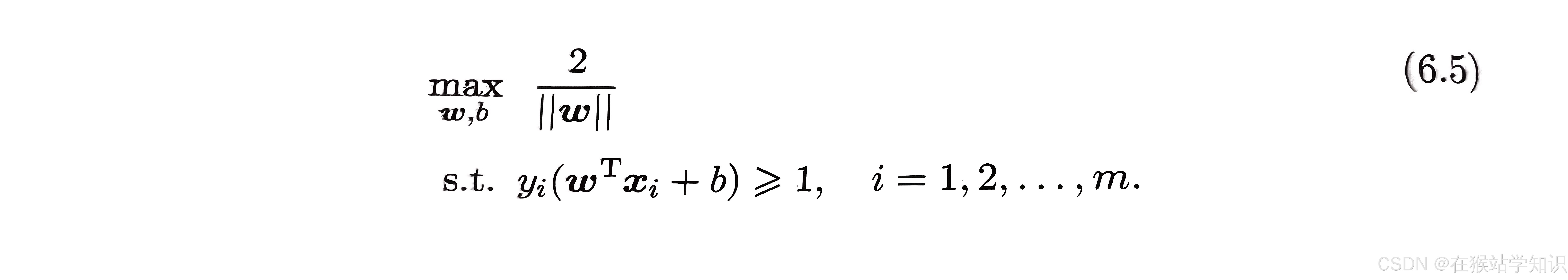
显然，为了最大化间隔，仅需最小化‖w‖，这就等价于最小化‖w‖²（二次函数比一次函数能更直观的优化目标）。于是，式(6.5)可重写为
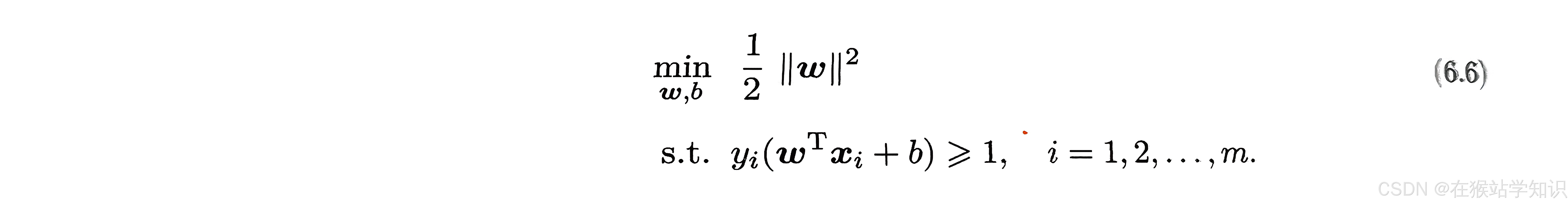
PS：除以2是为了方便梯度下降等优化算法的迭代
二、对偶问题
-----解释对偶问题，如果清楚对偶问题可跳过下文，直接看正文----
对偶问题是线性规划优化问题的另一种表述方式。在对偶问题中，优化的目标函数和约束条件都与原始问题不同，但两个问题具有等价的最优解。通过解决对偶问题，可以间接地得到原始问题的最优解，这种方法称为对偶法。
对于一个凸优化问题（凸优化问题是数学优化领域中的一个重要分支，主要研究目标函数和约束条件均为凸函数的优化问题。凸优化问题具有良好的性质，如局部最优解即为全局最优解，这使得凸优化问题在理论和实际应用中都非常重要。），其对偶问题可以通过拉格朗日对偶性得到。对于原始问题：
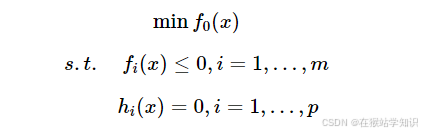
这意味着，对于任意可行的拉格朗日乘子，对偶问题的最优解都提供了原始问题的下界。如果对偶问题的解与下界相等，那么它就是原始问题的最优解。
需要注意的是，对偶问题的约束条件通常比原始问题的约束条件更少，并且在许多情况下更容易求解。简单理解对偶问题就是：假设原始问题是线性规划中求解最大值，则对偶问题就是线性规划中求解的是最小值，从意义上理解就是把它做一个变换。举个简单例子：求解y=1/x（x∈(0，+∞)）的最小值，可以对其做一个变换，问题就变成是求x的最大值。可以类比成对称函数，将问题做一个对称变换的意思。
KKT条件（Karush-Kuhn-Tucker Conditions）是优化理论中用于求解带有约束的非线性规划问题的一组必要条件。KKT条件在凸优化问题中尤为重要，因为对于凸优化问题，KKT条件不仅是必要条件，也是充分条件，即满足KKT条件的点就是全局最优解。KKT有一个基本型公式，后文会给出，这里由于篇幅问题，不在讨论KKT问题，如果要具体深刻的理解KKT条件，可以见此篇博客。https://blog.csdn.net/weixin_52808620/article/details/130599802
-----------正文由此开始-----------
我们希望求解式(6.6)来得到大间隔划分超平面所对应的模型：
注意到式(6.6)本身是一个凸二次规划问题（因为有平方），这里可以用拉格朗日乘子法可得到其“对偶问题”。由于这里存在大量复杂的数学公式推导，这里不给出其推导过程，只给出最后丶公式。
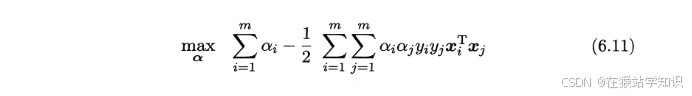
从推导出来的公式，可以显示出支持向量机的一个重要性质：训练完成后，大部分的训练样本都不需保留，最终模型仅与支持向量有关。
如何求解式(6.11)？不难发现这个是一个二次规划问题，可使用通用的二次规划算法来求解；然而，该问题的规模正比于训练样本数，这会在实际任务中造成很大的开销。为避开这个障碍，人们通过利用问题本身的特性，提出很多高效算法，SMO是其中一个著名的代表。（若有兴趣，可自行了解SMO，这里不再赘述SMO算法）。
三、核函数
在本章前面的讨论中，假设训练样本是线性可分的，即存在一个划分超平面能将训练样本正确分类。然而在现实任务中，原始样本空间也许并不存在一个能正确划分两类样本的超平面。如下图所示，“异或”问题就不是线性可分的。
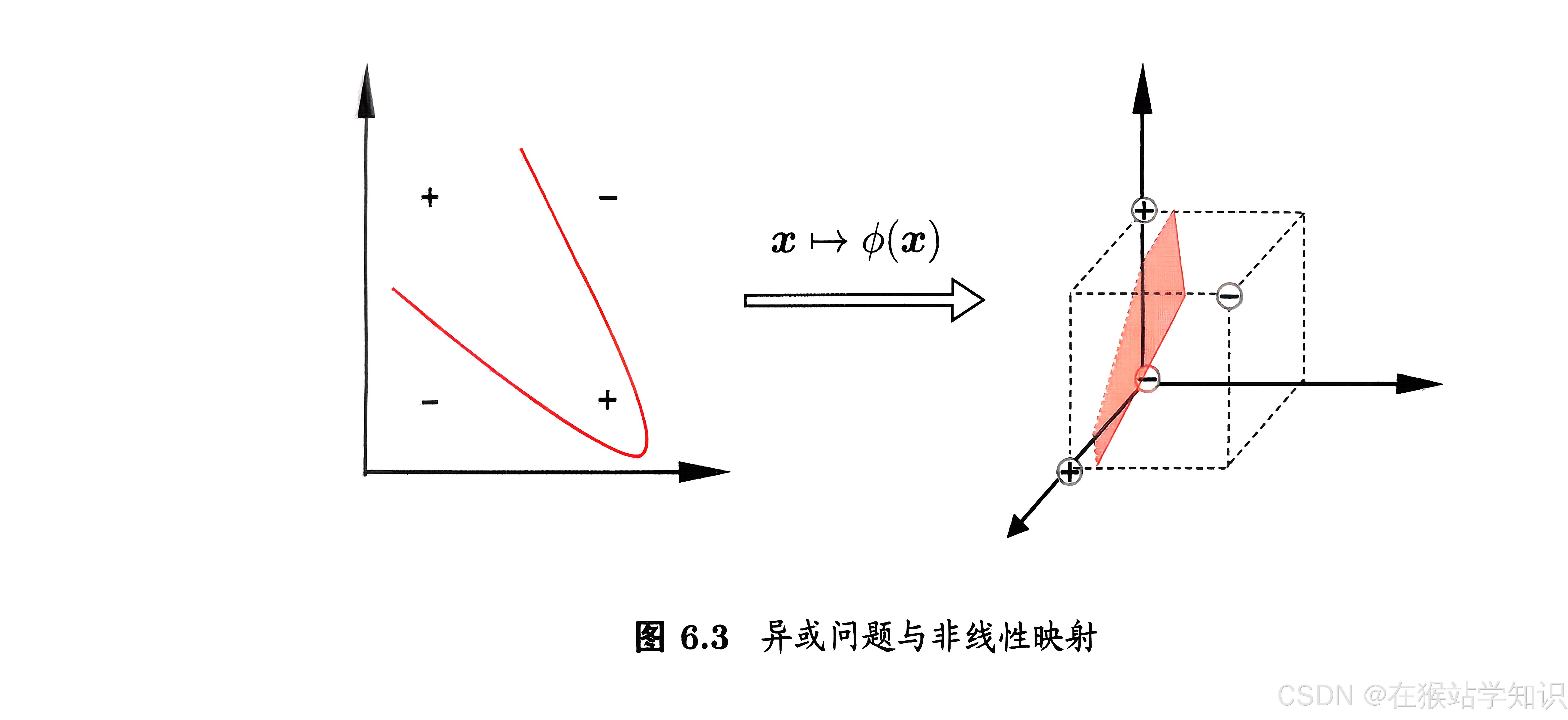
对于这样的问题， 可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。如上图所示，若将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超平面。幸运的是，如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。
令∅(x)表示x映射后的特征向量，于是，在特征空间中划分超平面所对应的模型可表示为：
采用支持向量机的基本型及其对偶问题 ，则为：
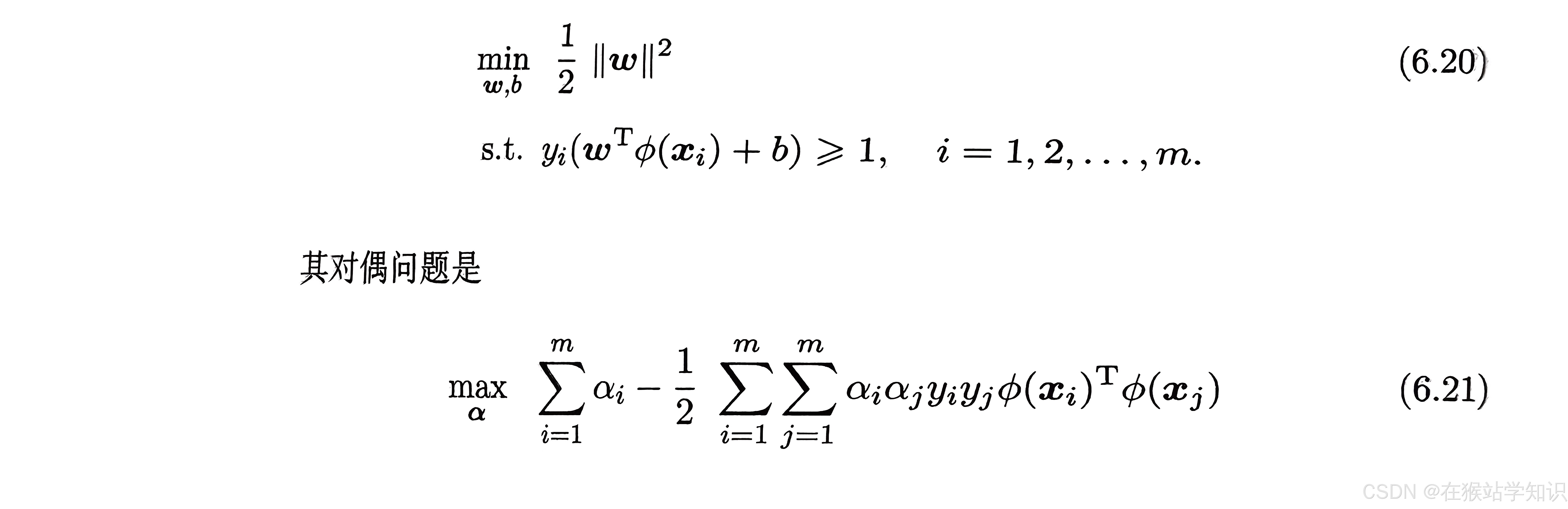
求解式(6.21)涉及计算，这是样本
与
映射到特征空间之后的内积。由于特征空间维数可能很高，甚至可能是无穷维，故直接计算是困难的。为避开此障碍，可以设想这样一个函数：
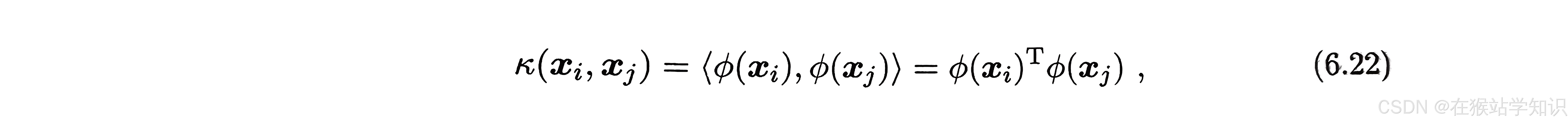
即与
在特征空间的内积等于它们在原始样本空间中通过函数k(·,·)计算的结果。有这样的函数（核函数），就不用计算高维甚至无穷维特征空间中的内积。故，可重写为：
这里的函数k(·,·)就是“核函数”，式(6.24)就是“支持向量展式”。
显然，若已知合适映射∅(·)的具体形式，则可写出核函数k(·,·)。但在现实任务中我们通常不知道∅(·)是什么形式，那么，合适的核函数是否一定存在呢？什么样的核函数能做核函数呢？
定理6.1表明：只要一个对称函数所对应的核矩阵是半正定，它就能作为核函数使用。事实上，对于一个半正定核矩阵，总能找到一个与之对应的映射∅。
通过前面的讨论可知，我们希望样本在特征空间内线性可分，因此特征空间的好坏对支持向量机的性能至关重要。需要注意的是，在不知道特征映射的形式时，我们并不知道什么样的核函数是合适的，而核函数也仅是隐式地定义了这个特征空间。于是，“核函数选择”成为支持向量机的最大变数。下面给出一些几种常见的核函数：
此外，还可以通过核函数之间组合得到，如：线性组合、直积、任意函数的乘积等。
四、软间隔与正则化
在前面的讨论中，一直假定训练样本在样本空间或特征空间中是线性可分的，即存在一个超平面能将不同类的样本完全划分开。然而，在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分。
缓解该问题一个办法是允许支持向量机在一些样本上出错。为此，要引入“软间隔”的概念，如下图所示：
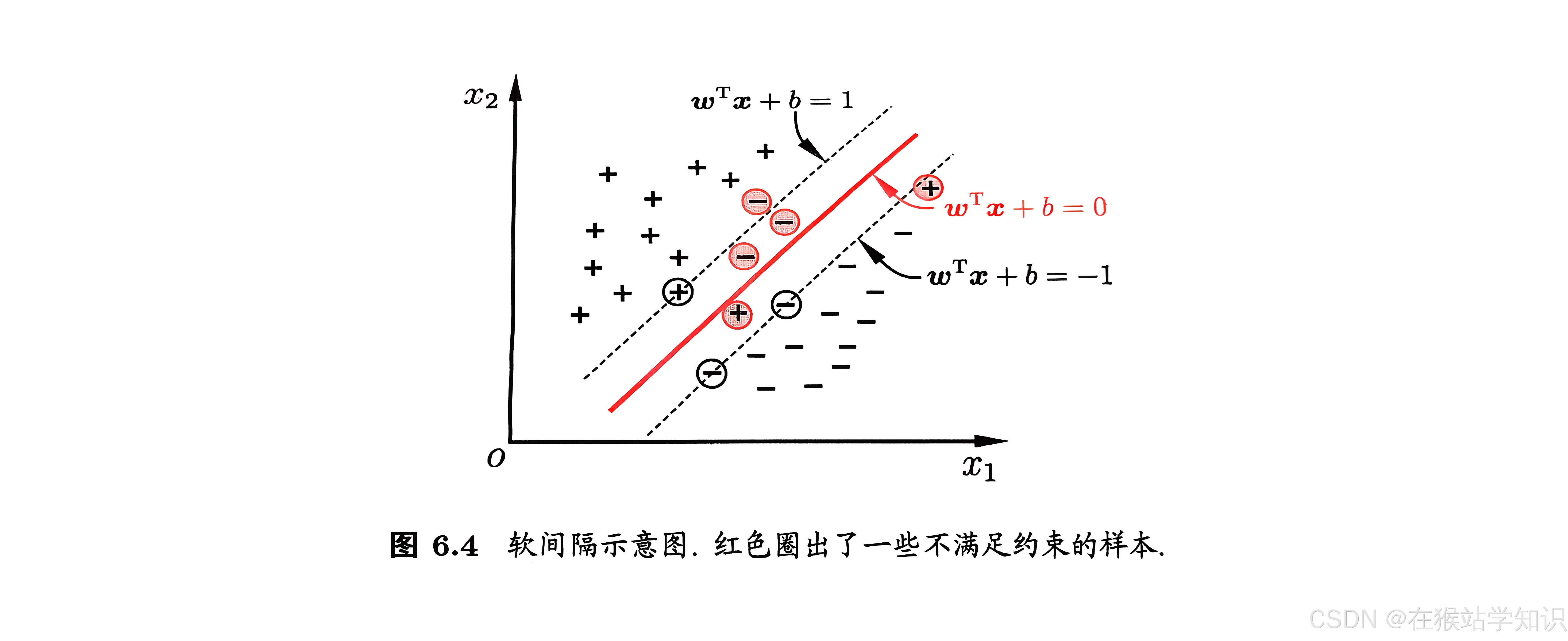
具体来说，前面介绍的支持向量机形式是要求所有样本均满足约束式，即所有样本都必须划分正确，这称为“硬间隔”，而软间隔则是允许某些样本不满足约束。当然，在最大化间隔的同时，不满足约束样本应尽可能少。于是，优化目标为：
然而，非凸、非连续，数学性质不太好，不好求解，则通常用一些函数来代替，称为“替代函数”。它具有较好的数学性质，下面给出三种常见的替代损失函数。
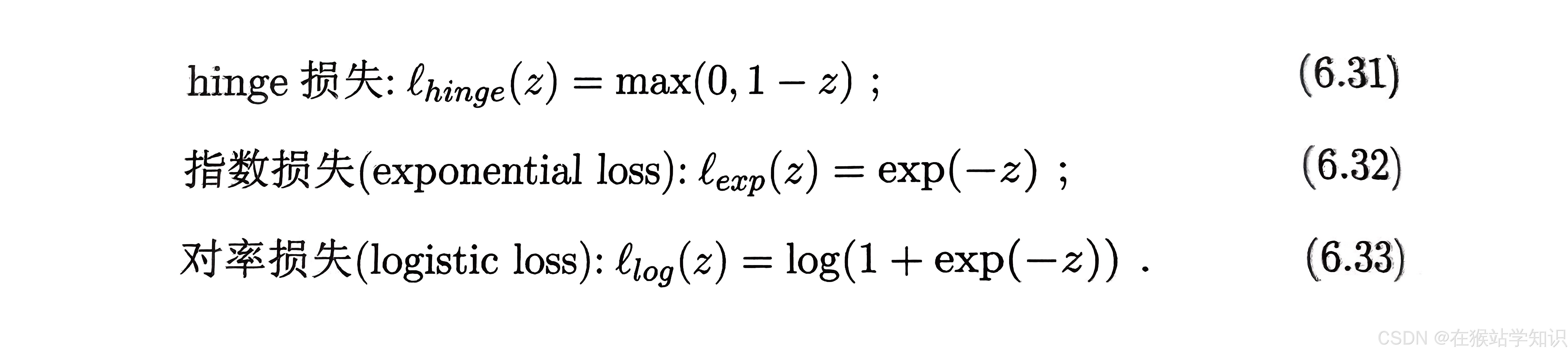
这样，把0/1损失函数换成别的替代损失函数可以得到其他学习模型，这些模型的性质与所用的替代函数直接相关，但它们有一个共性：优化目标中的第一项用来描述划分超平面的“间隔”大小，另一项用来表述训练集上的误差，可写为一般式：
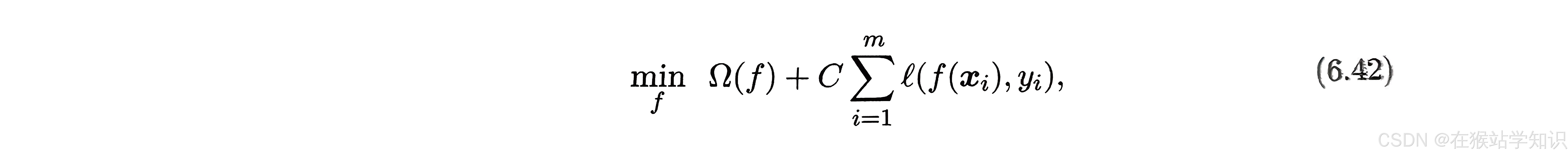
其中Ω(f)称为“结构风险”，用于描述模型f的某些性质；第二项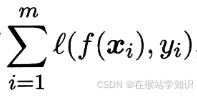 
称为“经验风险”，用于描述模型与训练数据的契合程度；C用于对二者进行折中。从经验风险最小化的角度来看，Ω(f)表述了我们希望获得具有何种性质的模型（例如希望获得复杂度较小的模型），这为引入领域知识和用户意图提供了途径；另一方面，该信息有助于削减假设空间，从而降低了最小化训练误差的过拟合风险。从这个角度来说，式(6.42)称为“正则化”问题，Ω(f)称为正则化项, C则称为正则化常数。Lp范数是常用的正则化项，其中L2范数||ω||2倾向于的分量取值尽量均衡，即非零分量个数尽量稠密，而L0范数||ω||0和L1范数||ω||1则倾向于w的分量尽量稀疏，即非零分量个数尽量少。
PS：正则化可以理解为一种“罚函数法”，即对不希望得到的结果施以惩罚，从而使得优化过程趋向于希望目标。从贝叶斯估计的角度来看，正则化可认为是提供了模型的先验概率。（先验概率是指在没有任何新的观测数据或信息的情况下，基于已有的知识、经验或历史数据对某一事件或假设的概率估计。）
五、支持向量回归（SVR）
之前讨论的是分类问题，现在考虑回归问题，给定训练样本，
。对样本(x,y)来说，传统回归模型通常直接基于模型输出f(x)与真实输出y之间的差别来计算损失，当且仅当f(x)与y完全相同时，损失才为0。与此不同，SVR假设我们能容忍f(x)与y之间最多有ε的偏差，即仅当f(x)与y之间的差别绝对值大于ε时才计算损失。如下图所示，这相当于以f(x)为中心，构建了一个宽度为2ε的间隔带，若训练样本落入此间隔带，则预测是正确的。
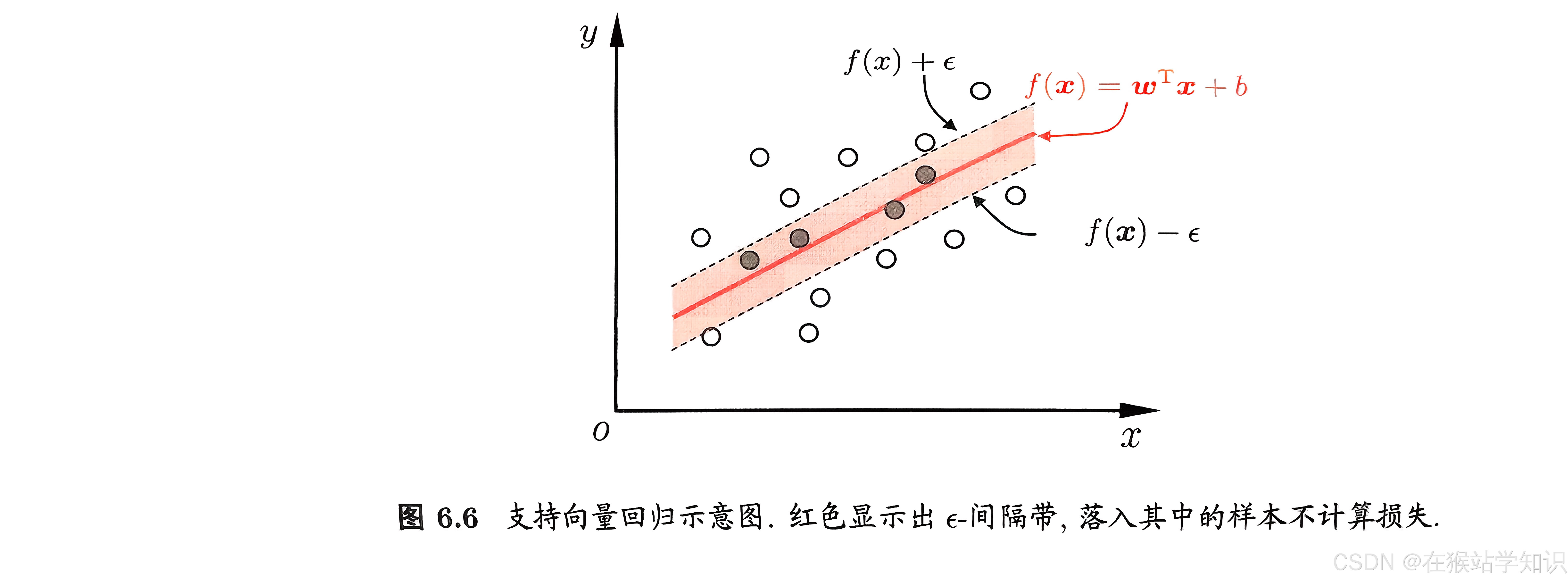
下文就是在讨论将SVR问题进行数学公式化，跟上文的分类问题相似，直至用一个最终的数学公式来解释SVR，这里为减少数学公式理解的，后文就不再叙述。这里就给出最终的SVR可表示为：
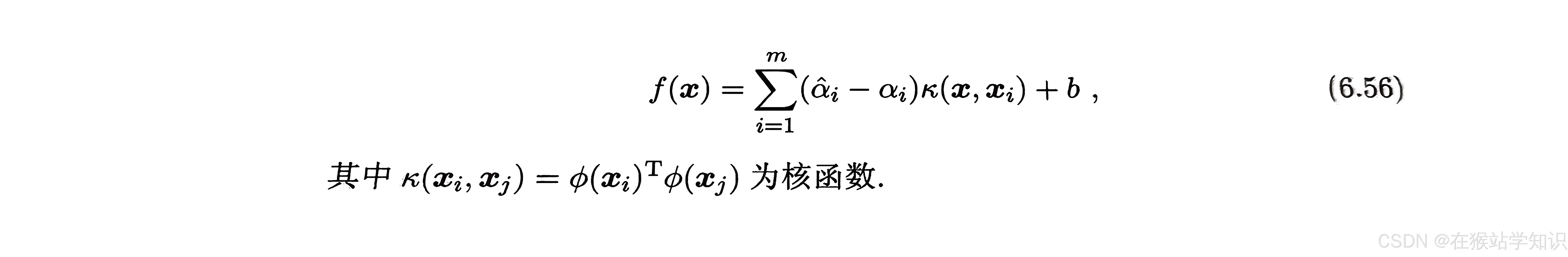
六、核方法
目前发展出一系列基于核函数的学习方法，统称为“核方法”。最常见的，是通过“核化”（即引入核函数）来讲线性学习器拓展为非线性学习器，这里的拓展需要较强的数学基础。西瓜书上做了一个以线性判别分析为例来演示如何通过核化来对其进行非线性拓展，从而得到“核线性判别分析”（KLDA），但里面有大量复杂的数学公式的推导，这里不再给出，感兴趣的可以阅读原文P137。
说几句心里话，作者这几个月一直在啃这本西瓜书，里面真的很晦涩难懂，作者一度想放弃，但还的坚持下来了。可能有读者觉得，这样的学习不深刻，没有用处。但我想说的是，只要你觉得你学到了东西，你觉得有用那就有用。很多东西，我们目前可能真的无法理解，但随着时间和阅历的增长，某一刻我们可能就能理解其内在含义。就跟作者在学习408（计算机学科专业基础综合），里面的东西都是互相交汇掺杂的。当你学习某一个知识的时候，你无法立即理解它，因为它可能需要其他的前置知识。但当你学习了其他知识，正好可以跟它相通时，你这一刻就能理解透彻的。所以，希望读者不要放弃，这同时也是在勉励作者自己不要放弃，一定要啃完这本书，然后更完这个系列。愿与君共勉！！！