前言:
本专栏属于数据结构相关内容,附带一些代码加深对一些内容的理解,为方便读者观看,本专栏内的所有文章会同时附带C语言和Python对应的代码,(可自行通过目录跳转到对应的部分)辅助不同主修语言的读者去更好的理解对应的内容,若是代码0基础的读者,可先去博主其他专栏学习一下基础的语法及知识点:
魔法天才的跳转链接:
C语言:C基础_Gu_shiwww的博客-CSDN博客
Python语言:python1_Gu_shiwww的博客-CSDN博客
其他数据结构内容可见:数据结构_Gu_shiwww的博客-CSDN博客
1 双向链表
双向链表即可以从前往后或者从后往前找,这就意味着链表的结点就不能只有一个指针域next了,还需要一个指向前驱结点的指针域prior。
下面分两种语言去编写代码实现双向链表
Python语言编程实现双向链表:
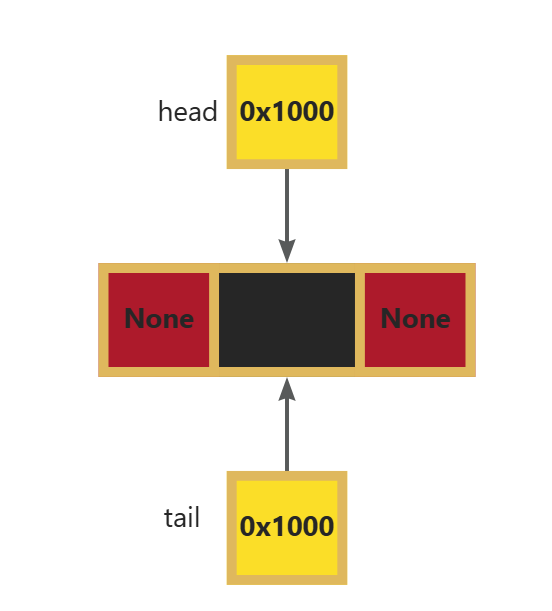
P.1 双向链表的结点及初始化
class Node:
def __init__(self):
self.prior = None # 指向前一个节点的指针
self.next = None # 指向下一个节点的指针
self.data = None # 数据域(在这个空链表的例子中,数据域未被使用)
class DoubleLinkedList:
def __init__(self):
self.head = Node() # 头节点,初始化时不存储实际数据
self.tail = self.head # 尾指针初始时指向头节点,因为链表为空
self.len = 0 # 当前链表的长度P.2 双线链表的插入
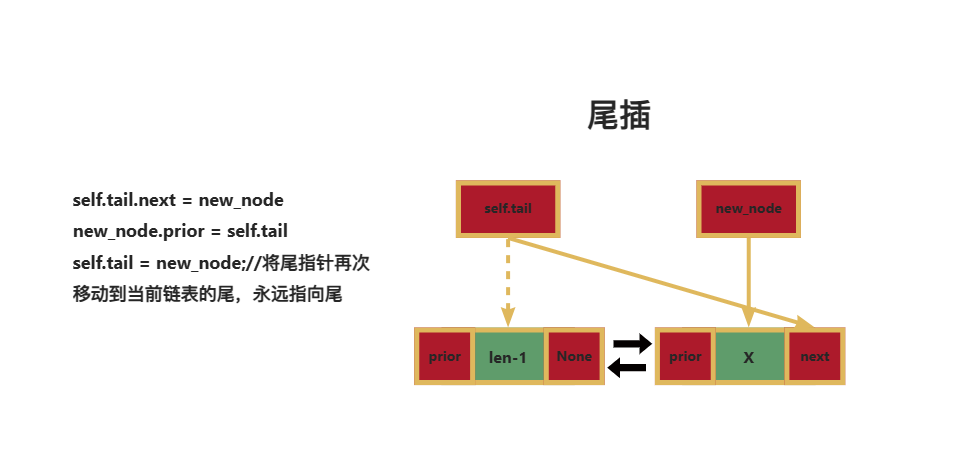
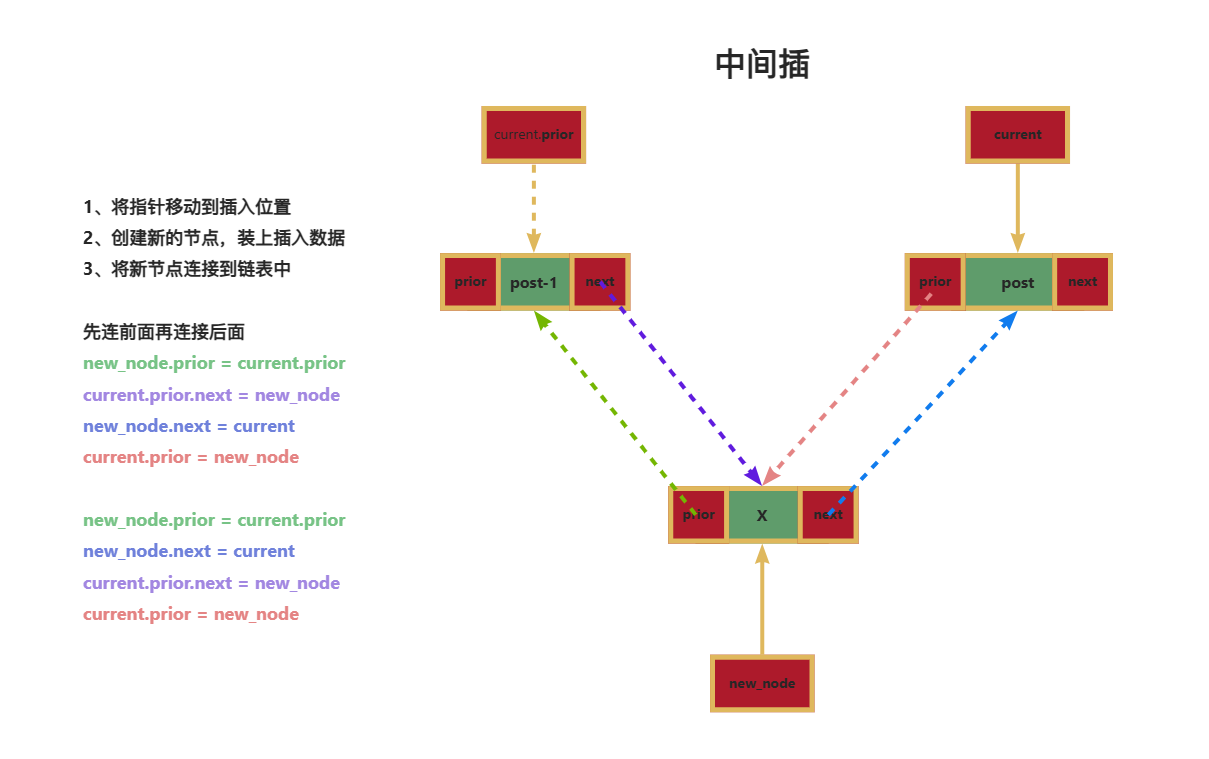
双向链表的插入有两种,一种是尾插,一种是中间插,下面给到两种插入方式图示:
class Node:
def __init__(self, data=None):
self.data = data # 数据域
self.prior = None # 指向前一个节点的指针
self.next = None # 指向下一个节点的指针
class DoubleLinkedList:
def __init__(self):
self.head = Node() # 头节点,作为哑节点(不存储实际数据)
self.tail = self.head # 尾指针初始时指向头节点
self.len = 0 # 当前链表的长度
def insert(self, position, data):
# 容错判断
if position < 0 or position > self.len:
print("插入位置无效!")
return -1
# 创建一个新的节点
new_node = Node(data)
# 将节点链接到链表中
if position == self.len: # 插入到链表尾部
self.tail.next = new_node
new_node.prior = self.tail
self.tail = new_node # 更新尾指针
else: # 插入到链表中间或头部
if position < self.len // 2: # 插入位置在前半部分,从头向后遍历
current = self.head
for _ in range(position + 1):
current = current.next
else: # 插入位置在后半部分,从尾向前遍历
current = self.tail
for _ in range(self.len - position - 1):
current = current.prior
# 进行插入操作(先连前面,再连后面)
new_node.prior = current.prior
current.prior.next = new_node
new_node.next = current
current.prior = new_node
self.len += 1 # 链表长度加1
return 0
# 测试代码
if __name__ == "__main__":
dll = DoubleLinkedList()
dll.insert(0, 10) # 在位置0插入数据10
dll.insert(1, 20) # 在位置1插入数据20
dll.insert(1, 15) # 在位置1插入数据15(应该在20之前)
dll.insert(3, 30) # 在位置3插入数据30
# 打印链表内容(从头节点后的第一个节点开始,直到尾节点前的最后一个节点)
current = dll.head.next
while current != dll.tail.next:
print(current.data, end=" -> ")
current = current.next
print("None") # 用None表示链表末尾
P.3 双向链表的删除
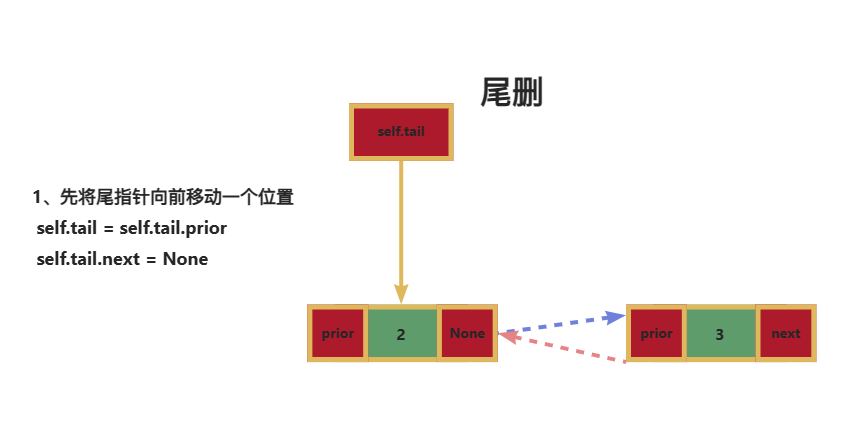
同样,删除方式也有两种:尾删和中间删
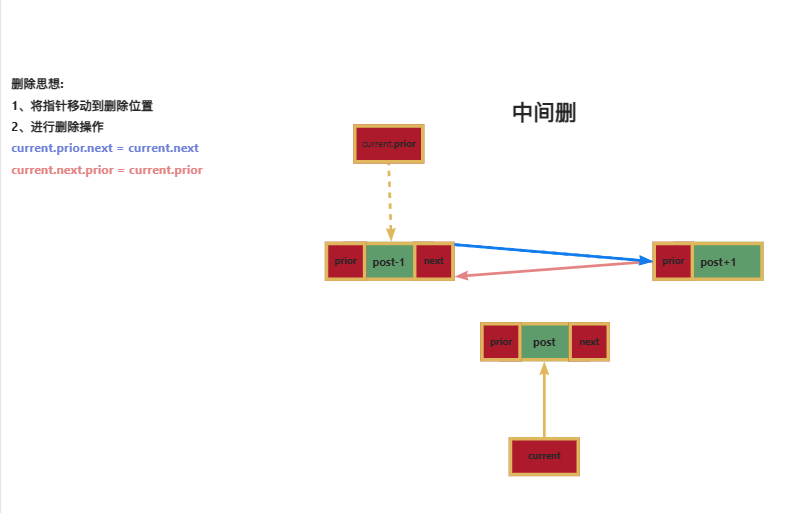
前驱 post 后继
| | |
current->prior current current->next
1. 给前驱的next域赋值
2. 给后继的prior域赋值
# 删除双向链表指定位置的数据
def delete(self, position):
# 容错处理
if position < 0 or position >= self.len:
print("删除位置无效!")
return -1
# 2.对删除位置进行分析,分为两种情况
# 如果删除的是链表最后一个节点
if position == self.len - 1:
# 将尾指针向前移动一个位置
self.tail = self.tail.prior
self.tail.next = None
else:
# 找到要删除的节点的前一个节点和后一个节点
if position < self.len // 2: # 如果位置在前半部分,从头向后遍历
current = self.head
for _ in range(position + 1):
current = current.next
else: # 如果位置在后半部分,从尾向前遍历
current = self.tail
for _ in range(self.len - position - 1):
current = current.prior
# 断开链接并进行删除操作(在Python中,这会导致被删除节点被垃圾回收)
current.prior.next = current.next
current.next.prior = current.prior
# 双向链表的长度减1
self.len -= 1
return 0
# 判断双向链表是否为空
def is_empty(self):
return self.len == 0
# 求双向链表的长度
def length(self):
return self.lenC语言编程实现双向链表
C.1 创空
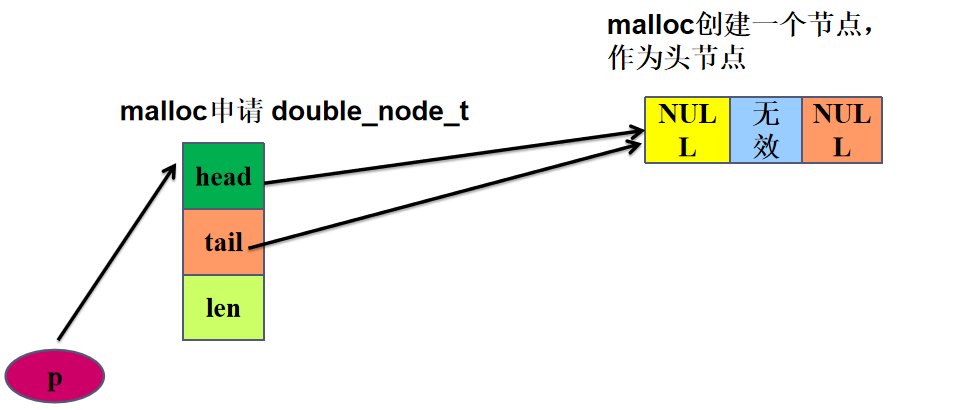
C.2 插入
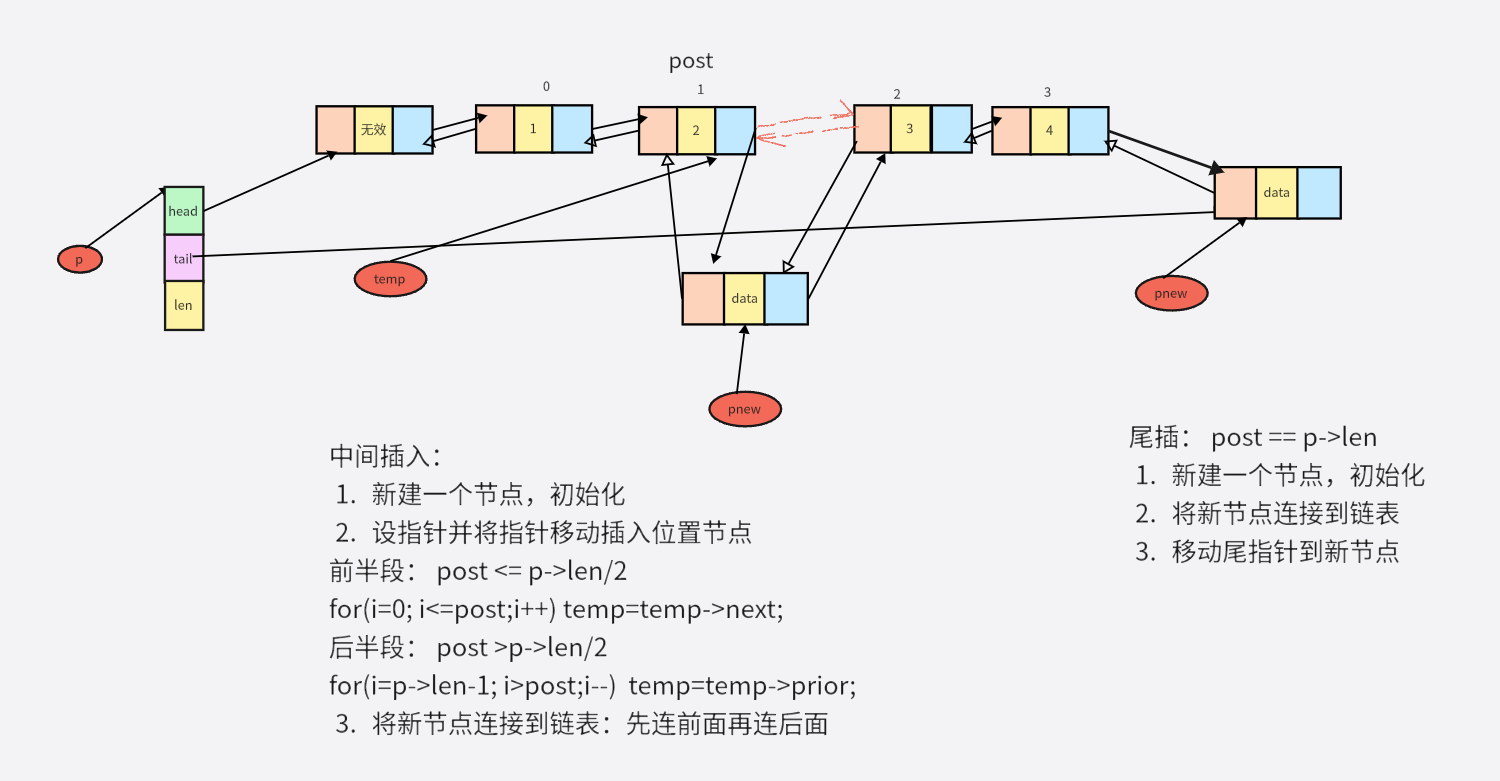
C.3 删除
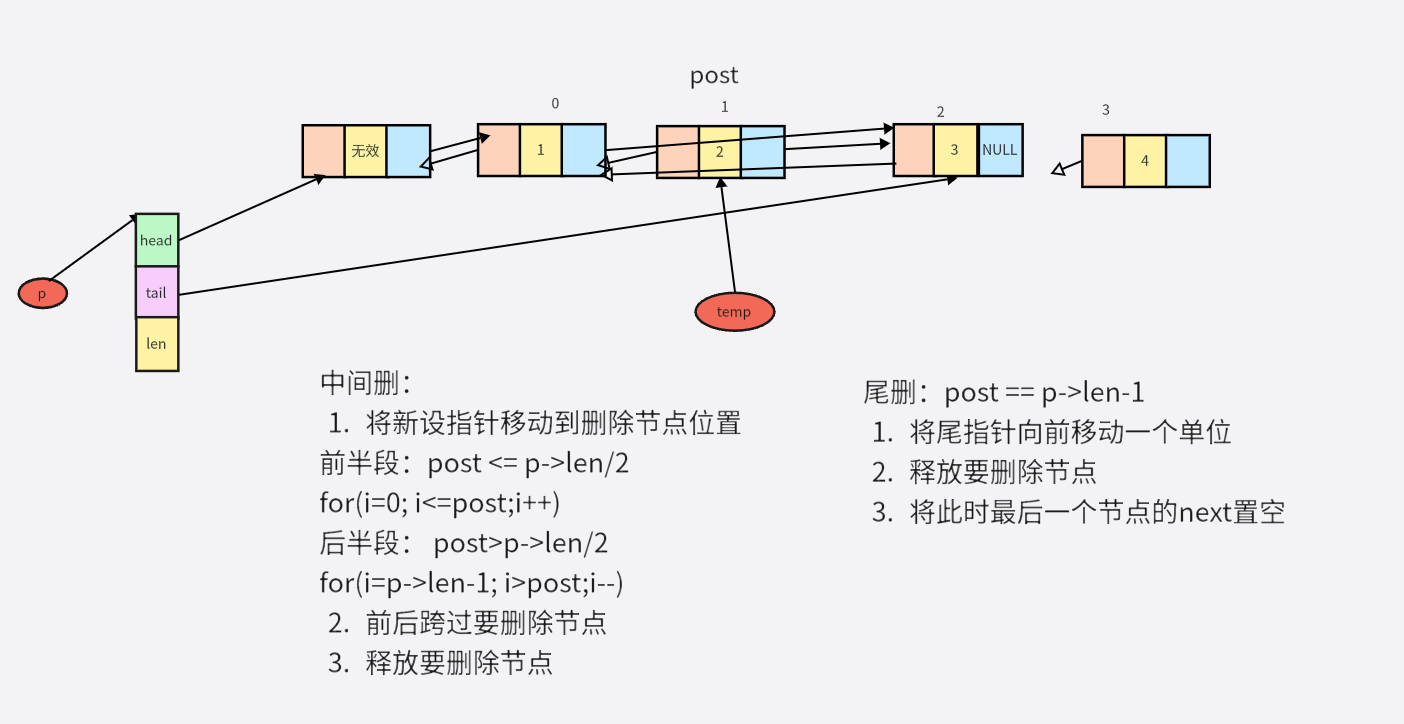
C.3.* 按数据删除
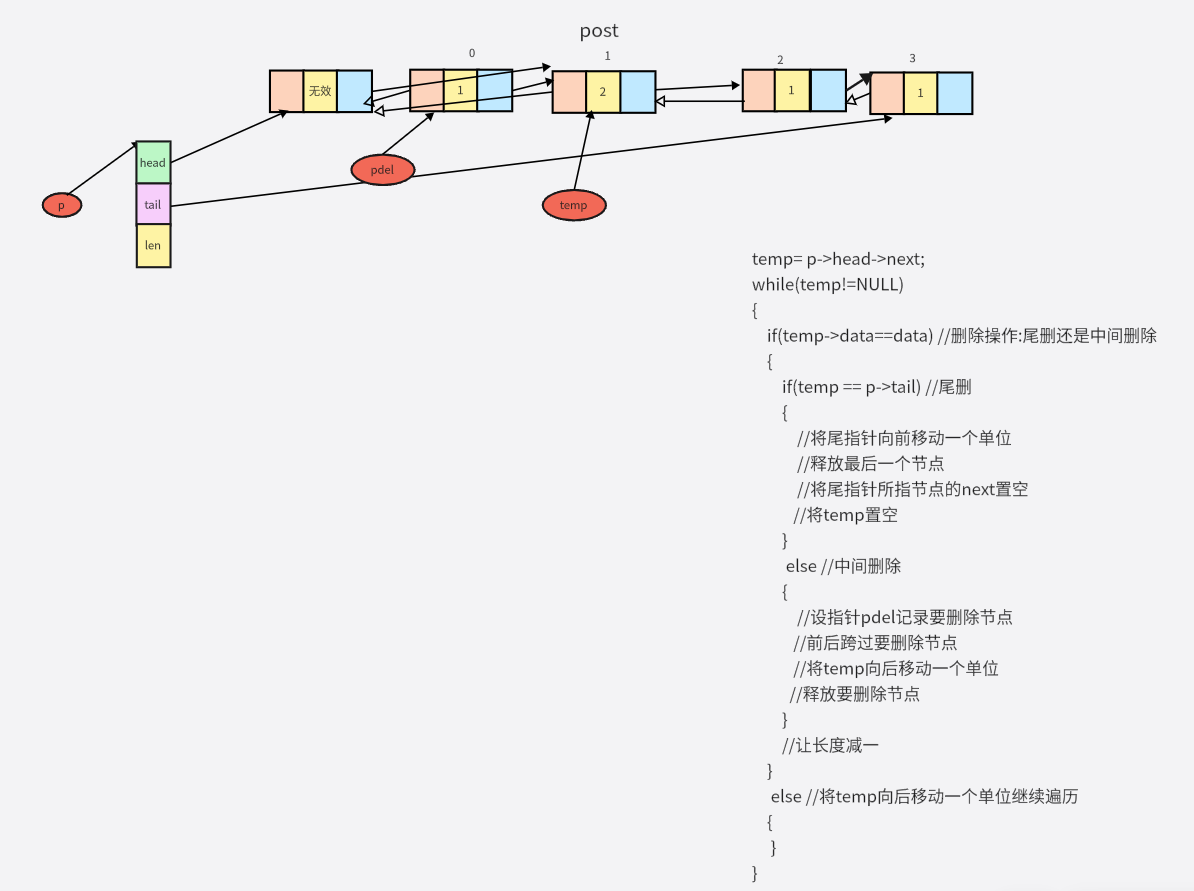
思想:从头节点后节点开始用指针temp遍历,相当于遍历无头链表,遇到需要删除节点的就用pdel指向它然后删除,如果不需要删除则temp继续往后走一个单位。这里因为是双向链表可以找到前驱,所以不需要每次指向被删除节点的前一个然后跨过了。
- 将新节点的 prior 指针指向直接前驱节点。
- 将直接前驱节点的 next 指针指向新节点。
C.4 完整代码
#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct node_t
{
datatype data; //数据域
struct node_t *next; //后继指针
struct node_t *prior; //前驱指针
} link_node_t, *link_node_p;
//封装头尾指针和长度结构体
//思想上有点像链式队列
typedef struct doublelinklist
{
link_node_p head;
link_node_p tail;
int len;
} double_list_t, *double_list_p;
//创建一个空的双向链表
double_list_p createEmptyDoubleLinkList()
{
//1. 开辟双向链表结构体空间
double_list_p p = (double_list_p)malloc(sizeof(double_list_t));
if (NULL == p)
{
perror("p malloc err");
return NULL;
}
//2.初始化结构体空间
p->len = 0;
p->head = p->tail = (link_node_p)malloc(sizeof(link_node_t));
if (NULL == p->head)
{
perror("head err");
return NULL;
}
//3. 初始化头节点
p->head->next = NULL;
p->head->prior = NULL;
return p;
}
//向双向链表的指定位置插入数据 post位置, data数据
int insertIntoDoubleLinkList(double_list_p p, int post, datatype data)
{
//1. 容错判断
if (post < 0 || post > p->len)
{
printf("insert err\n");
return -1;
}
//2. 新建一个节点,并初始化
link_node_p pnew = (link_node_p)malloc(sizeof(link_node_t));
if (NULL == pnew)
{
perror("pnew err");
return -1;
}
pnew->data = data;
pnew->next = pnew->prior = NULL;
//3. 将新节点插入到链表,分情况:尾插还是中间插入
if (post == p->len)
{
//(1) 将新节点连接到链表
pnew->prior = p->tail;
p->tail->next = pnew;
//(2) 移动尾指针到新节点
p->tail = pnew;
}
else //中间插入
{
//(1) 设指针temp并移动到插入位置节点,分前后半段
link_node_p temp;
if (post < p->len / 2) //前半段从前往后移动
{
temp = p->head;
for (int i = 0; i <= post; i++)
temp = temp->next;
}
else //后半段从后往前移动
{
temp = p->tail;
for (int i = p->len - 1; i > post; i--)
temp = temp->prior;
}
//(2) 将新节点连接到链表(先连前面再连后面)
pnew->prior = temp->prior;
temp->prior->next = pnew;
pnew->next = temp;
temp->prior = pnew;
}
//4. 让长度加一
p->len++;
return 0;
}
//遍历双向链表
void showDoubleLinkList(double_list_p p)
{
link_node_p temp = NULL;
//正向遍历
printf("正向遍历: ");
temp = p->head;
while (temp->next != NULL) //有头链表遍历
{
temp = temp->next;
printf("%d ", temp->data);
}
printf("\n");
//反向遍历
printf("反向遍历: ");
temp = p->tail;
while (temp != p->head) //类似于无头链表遍历
{
printf("%d ", temp->data);
temp = temp->prior;
}
printf("\n");
}
//判断链表是否为空
int isEmptyDoubleLinkList(double_list_p p)
{
return p->len == 0;
}
//删除双向链表指定位置数据
int deletePostDoubleLinkList(double_list_p p, int post)
{
//1.容错判断
if (isEmptyDoubleLinkList(p) || post < 0 || post >= p->len)
{
printf("delete err");
return -1;
}
//2. 删除操作,分情况讨论:尾删还是中间删
if (post == p->len - 1) //尾删
{
//将尾指针向前移动一个单位
p->tail = p->tail->prior;
//释放要删除节点
free(p->tail->next);
//将此时最后一个节点的next置空
p->tail->next = NULL;
}
else //中间删
{
link_node_p temp;
//(1)将指针遍历到删除节点位置,分前后半段
if (post <= p->len / 2) //前半段从前向后遍历
{
temp = p->head;
for (int i = 0; i <= post; i++)
temp = temp->next;
}
else //后半段从后向前遍历
{
temp = p->tail;
for (int i = p->len - 1; i > post; i--)
temp = temp->prior;
}
//(2)跨过要删除节点
temp->prior->next = temp->next;
temp->next->prior = temp->prior;
//(3)释放要删除节点
free(temp);
}
//3.长度减一
p->len--;
return 0;
}
//删除双向链表中的指定数据 data代表删除所有出现的data数据
void deleteDataDoubleLinkList(double_list_p p, datatype data)
{
link_node_p temp = p->head->next; //设指针指向头节点的后一个
while (temp != NULL) //相当于遍历无头链表
{
if (temp->data == data) //删除操作:尾删还是中间删除
{
if (temp == p->tail) //尾删
{
//将尾指针向前移动一个单位
p->tail = p->tail->prior;
//释放最后一个节点
free(p->tail->next);
//将尾指针所指节点的next置空
p->tail->next = NULL;
//将temp置空
temp = NULL;
}
else //中间删除
{
//设指针pdel记录要删除节点
link_node_p pdel = temp;
//前后跨过要删除节点
temp->prior->next = temp->next;
temp->next->prior = temp->prior;
//将temp向后移动一个单位
temp = temp->next;
//释放要删除节点
free(pdel);
}
//让长度减一
p->len--;
}
else //将temp向后移动一个单位继续遍历
{
temp = temp->next;
}
}
}
//查找指定数据出现的位置 data被查找的数据
int searchPostDoubleLinkList(double_list_p p, datatype data)
{
link_node_p temp = p->head;
int post = 0;
while (temp->next != NULL)
{
temp = temp->next;
if (temp->data == data)
return post;
post++;
}
return -1; //代表没找到
}
//修改指定位置的数据,post修改的位置 data被修改的数据
int changeDataDoubleLinkList(double_list_p p, int post, datatype data)
{
//1.容错判断
if (isEmptyDoubleLinkList(p) || post < 0 || post >= p->len)
{
printf("change err\n");
return -1;
}
//2.设指针移动到要修改节点位置
link_node_p temp;
if (post <= p->len / 2) //前半段
{
temp = p->head;
for (int i = 0; i <= post; i++)
temp = temp->next;
}
else //后半段
{
temp = p->tail;
for (int i = p->len - 1; i > post; i--)
temp = temp->prior;
}
//3.修改节点数据
temp->data = data;
return 0;
}
int main(int argc, char const *argv[])
{
double_list_p p = createEmptyDoubleLinkList();
insertIntoDoubleLinkList(p, 0, 1);
insertIntoDoubleLinkList(p, 1, 2);
insertIntoDoubleLinkList(p, 2, 3);
insertIntoDoubleLinkList(p, 3, 1);
insertIntoDoubleLinkList(p, 4, 1);
printf("2 post is: %d\n", searchPostDoubleLinkList(p, 2));
changeDataDoubleLinkList(p,1, 100);
showDoubleLinkList(p);
deletePostDoubleLinkList(p, 1);
showDoubleLinkList(p);
deleteDataDoubleLinkList(p, 1);
showDoubleLinkList(p);
return 0;
}
2 双向循环链表
思想和单向循环一样,只需要将双向链表尾的next和头的prior双向链接即可。
以下是利用代码实现双向循环链表的功能以解决约瑟夫问题(约瑟夫问题读者可自行查询了解)
Python
class Node:
def __init__(self, data):
self.data = data # 节点数据
self.prior = None # 指向前一个节点的指针
self.next = None # 指向下一个节点的指针
class DoubleLinkedList:
def __init__(self):
self.head = None # 链表头指针
self.tail = None # 链表尾指针
def append(self, data):
# 在链表末尾添加新节点
new_node = Node(data)
if not self.head:
# 如果链表为空,则新节点既是头节点也是尾节点
self.head = self.tail = new_node
else:
# 否则,将新节点添加到链表末尾
self.tail.next = new_node
new_node.prior = self.tail
self.tail = new_node
def make_circular(self):
# 使链表形成循环
if self.head and self.tail:
self.tail.next = self.head
self.head.prior = self.tail
def josephus_problem(self, all_num, start_num, kill_num):
# 解决约瑟夫问题
# 填充循环双向链表
for i in range(1, all_num + 1):
self.append(i)
self.make_circular()
# 移动到起始位置
current = self.head
for _ in range(start_num - 1):
current = current.next
# 解决约瑟夫问题
while current.next != current: # 当链表中不止一个节点时
# 移动到要删除的节点
for _ in range(kill_num - 1):
current = current.next
# 删除当前节点
print(f"杀死的是 ------- {current.data}")
if current.prior:
current.prior.next = current.next
if current.next:
current.next.prior = current.prior
# 移动到删除节点后的下一个节点
current = current.next
# 打印最后剩下的节点(猴王)
print(f"猴王是 {current.data}")
# 主函数
if __name__ == "__main__":
dll = DoubleLinkedList() # 创建双向链表实例
all_num = int(input("请您输入猴子的总数: ")) # 输入猴子总数
start_num = int(input("从几号猴子开始数: ")) # 输入开始数数的猴子号码
kill_num = int(input("数到几杀死猴子: ")) # 输入数到几杀死猴子的号码
dll.josephus_problem(all_num, start_num, kill_num) # 解决约瑟夫问题
C语言
#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct node_t
{
datatype data;
struct node_t * prior;
struct node_t * next;
}link_node_t,*link_node_p;
typedef struct doublelinklist
{
link_node_p head;
link_node_p tail;
}double_list_t,*double_list_p;
int main(int argc, const char *argv[])
{
int i;
int all_num = 8;//猴子总数
int start_num = 3;//从3号猴子开始数
int kill_num = 3;//数到几杀死猴子
link_node_p h = NULL;
link_node_p pdel = NULL;//用来指向被杀死猴子的节点
printf("请您输入猴子的总数,开始号码,出局号码:\n");
scanf("%d%d%d",&all_num,&start_num,&kill_num);
//1.创建一个双向的循环链表
double_list_p p = (double_list_p)malloc(sizeof(double_list_t));//申请头指针和尾指针
if(NULL == p)
{
perror("malloc failed");
return -1;
}
p->head = p->tail = (link_node_p)malloc(sizeof(link_node_t));
if(NULL == p->tail)
{
perror("p->tail malloc failed");
return -1;
}
p->head->data = 1;
p->head->prior = NULL;
p->head->next = NULL;
//将创建n个新的节点,链接到链表的尾
for(i = 2; i <= all_num; i++)
{
link_node_p pnew = (link_node_p)malloc(sizeof(link_node_t));
if(NULL == pnew)
{
perror("pnew malloc failed");
return -1;
}
pnew->data = i;
pnew->prior = NULL;
pnew->next = NULL;
//(1)将新的节点链接到链表的尾
p->tail->next = pnew;
pnew->prior = p->tail;
//(2)尾指针向后移动,指向当前链表的尾
p->tail = pnew;
}
//(3)形成双向循环链表
p->tail->next = p->head;
p->head->prior = p->tail;
//调试程序
#if 0
while(1)
{
printf("%d\n",p->head->data);
p->head = p->head->next;
sleep(1);
}
#endif
//2.循环进行杀死猴子
h = p->head;
//(1)先将h移动到start_num处,也就是开始数数的猴子号码处
for(i = 1; i < start_num; i++)
h = h->next;
printf("start is:%d\n",h->data);
while(h->next != h)//当h->next == h 就剩一个节点了,循环结束
{
//(2)将h移动到即将杀死猴子号码的位置
for(i = 1; i < kill_num; i++)
h = h->next;
//(3)进行杀死猴子,经过上面的循环后,此时的h指向即将杀死的猴子
h->prior->next = h->next;
h->next->prior = h->prior;
pdel = h;//pdel指向被杀死猴子的位置
printf("kill is -------%d\n",pdel->data);
h = h->next;//需要移动,从杀死猴子后的下一个位置开始数
free(pdel);
}
printf("猴王是%d\n",h->data);
return 0;
}