ICCV 2025|从粗到细：用于高效3D高斯溅射的可学习离散小波变换-EW帮帮网

论文信息

题目：From Coarse to Fine: Learnable Discrete Wavelet Transforms for Efficient 3D Gaussian Splatting

从粗到细：用于高效3D高斯溅射的可学习离散小波变换

作者：Hung Nguyen、An Le、Blark Runfa Li、Truong Nguyen

源码：https://github.com/hungnguyen311299/AutoOpti3DGS

论文创新点

提出全新框架：论文提出AutoOpti3DGS框架，通过利用可学习离散小波变换（DWT）实现对输入图像自动的从粗到细频率调制，优化3D高斯溅射（3DGS）中的高斯数量。
创新频率调制方式：采用可学习的前向和逆离散小波变换，固定低通滤波器，将高通滤波器初始化为零，并通过辅助正交性损失逐渐激活精细频率。这种小波驱动的从粗到细过程，延迟了冗余精细高斯的形成，让3DGS先捕捉全局结构，必要时再细化细节。
设计自动调制策略：该框架替代了基于手工制作模糊的方法，基于可学习DWT自动地以从粗到细且适应数据集的方式调制输入图像频率，解决了手动选择模糊参数无法适应不同数据集、可能降低渲染质量的问题。

摘要

3D高斯溅射已成为新视图合成中的一种强大方法，能够快速训练和渲染，但代价是高斯基元的数量不断增加，给内存和带宽带来压力。作者引入了AutoOpti3DGS，这是一个训练时框架，可在不牺牲视觉保真度的情况下自动抑制高斯扩散。关键思想是将输入图像输入到一系列可学习的正向和反向离散小波变换中，其中低通滤波器保持固定，高通滤波器是可学习的并初始化为零，并且辅助正交损失逐渐激活精细频率。这种由小波驱动的从粗到精的过程延迟了冗余精细高斯的形成，使3DGS能够首先捕获全局结构，并仅在必要时细化细节。通过大量实验，AutoOpti3DGS只需要一个滤波器学习率超参数，可与现有的高效3DGS框架无缝集成，并且始终生成更稀疏的场景表示，更适合内存或存储受限的硬件。

关键词

3D高斯溅射；可学习离散小波变换；从粗到精频率调制

一、引言

3D高斯溅射（3DGS）已成为从2D图像集合重建3D场景的领先方法，能够在合理的训练时间内从新视角合成逼真的视图。其优势已使其在医学成像、机器人、虚拟现实和自动驾驶等领域得到广泛应用。

与前身NeRF相比，3DGS使用高斯表示3D场景，能够大幅减少训练时间并提高渲染质量。然而，训练期间高斯基元的数量没有得到明确控制，并且随着3DGS适应场景细节，其数量往往会迅速增长。因此，在保持有竞争力的渲染质量的同时减少高斯基元的数量，对于降低GPU内存使用和存储需求至关重要，特别是在边缘设备上。更少的高斯基元也有利于依赖每个高斯嵌入的方法，这些方法对于语义理解或对变形或光照变化进行建模很有用。

为此，作者提出了一种新颖的框架AutoOpti3DGS。它建立在Opti3DGS的基础上，Opti3DGS是一种旨在优化高斯数量的技术。Opti3DGS通过应用从粗到精的频率调制策略来实现这一点，在训练过程中逐步锐化输入图像。早期阶段的模糊图像会导致生成更大、更粗的高斯，随后随着引入更清晰的图像，这些高斯会分裂成代表精细细节的更小高斯。虽然Opti3DGS在不引入额外参数或优化步骤的情况下有效减少了高斯数量，但它依赖于手动选择的模糊参数，例如滤波器类型（如高斯、双线性、均值）、内核大小以及减小内核大小的调制时间表。所有这些都无法适应所使用的数据集，这可能会降低渲染质量。

AutoOpti3DGS通过纳入可学习的正向和反向离散小波变换（DWT）来解决这一限制，以对输入到3DGS的图像进行自适应的从粗到精调制。正向DWT将输入图像分解为捕获不同方向频率分量的子带。然后，反向DWT重建图像。通过固定低通滤波器并将高通滤波器初始化为零，AutoOpti3DGS从将粗重建作为输入图像开始。辅助损失促使高通滤波器趋向于其正交对应滤波器，鼓励高频精细细节逐渐出现。总之，贡献如下：

作者提出了一个框架AutoOpti3DGS，该框架通过利用可学习的DWT实现自动的从粗到精频率调制，从而优化3DGS的高斯数量。
通过全面的实验，所提出的AutoOpti3DGS展示了其在保持渲染质量的同时进一步减少高斯数量的能力，只需要预先定义学习率。它还能与当前高效的3DGS方法很好地互补，进一步减少高斯数量。

三、初步背景

3.1 3D高斯溅射

3DGS利用3D高斯来构建一个隐式3D场景，给定一组场景的多视图2D输入图像。在对3D场景进行建模后，可以获得来自新视角的渲染结果。每个高斯点由中心位置 $μ\mu$ 、不透明度 $σ\sigma$ 、协方差矩阵 $Σ\Sigma$ 和颜色 $c$ 参数化。为了优化这些参数，使用以下可微损失：
$L3DGS=(1−λ)L1(Xgt,X)+λLD−SSIM(Xgt,X)L_{3DGS} = (1 - \lambda)L_1(X_{gt}, X) + \lambda L_{D - SSIM}(X_{gt}, X)$
其中 $X_{gt}$ 和 $X$ 分别表示来自相同视角的真实图像和渲染图像。 $L_1$ 是逐像素平均绝对误差损失，而 $L_{D - SSIM}$ 是一个可微的SSIM损失函数，表示感知相似性。 $λ\lambda$ 是两者之间的平衡权重。

3.2 离散小波变换

给定一个非正方形的2D图像 $X$ ，正向DWT提供四个子带， $X_{LL}$ 、 $X_{LH}$ 、 $X_{HL}$ 、 $X_{HH}$ ，如下所示：
$\begin{cases} X_{LL} = L_0XL_1 \\ X_{LH} = H_0XL_1 \\ X_{HL} = L_0XH_1 \\ X_{HH} = H_0XH_1 \end{cases}$
其中 $L (\cdot)$ 和 $H (\cdot)$ 分别是对 $X$ 的列或行进行滤波的低通和高通分析矩阵。下标 ${0, 1\}$ 表示按列或按行滤波。一般来说，滤波矩阵是通过移动相同1D分析滤波器的行或列来构建的。例如，哈尔低通滤波器 $ℓ=[1/2,1/2]\ell = [1 / \sqrt{2}, 1 / \sqrt{2}]$ 和高通滤波器 $\sqrt{2}, 1 / \sqrt{2}]$ 。

在公式（2）中，滤波矩阵应用于两个维度。 $LL$ 子带是通过在两个维度上进行低通滤波得到的，捕获图像的粗略结构。 $L H$ 和 $H L$ 子带是通过在一个维度上进行低通滤波，在另一个维度上进行高通滤波得到的，突出水平或垂直细节。最后， $HH$ 子带是通过在两个方向上进行高通滤波得到的，捕获对角线细节。图2提供了DWT子带的可视化。

一个称为反向DWT的额外操作从子带重建原始图像 $X$ ：
$X^=L~0⊤XLLL~1⊤+H~0⊤XLHL~1⊤+L~0⊤XHLH~1⊤+H~0⊤XHHH~1⊤\hat{X} = \tilde{L}^{\top}_0 X_{LL} \tilde{L}^{\top}_1 + \tilde{H}^{\top}_0 X_{LH} \tilde{L}^{\top}_1 + \tilde{L}^{\top}_0 X_{HL} \tilde{H}^{\top}_1 + \tilde{H}^{\top}_0 X_{HH} \tilde{H}^{\top}_1$
其中 $X^\hat{X}$ 是重建图像。 $L~(⋅)\tilde{L}(·)$ 和 $H~(⋅)\tilde{H}(·)$ 分别是低通和高通合成矩阵。它们与分析矩阵的构建方式类似，但使用1D合成滤波器 $ℓ~\tilde{\ell}$ 或 $h~\tilde{h}$ 。在哈尔情况下，合成滤波器简单地由分析滤波器定义： $ℓ=ℓ~=[1/2,1/2]\ell = \tilde{\ell} = [1 / \sqrt{2}, 1 / \sqrt{2}]$ ， $h~=[1/2,−1/2]\tilde{h} = [1 / \sqrt{2}, -1 / \sqrt{2}]$ 是 $h$ 的翻转。

使用某一组分析和合成滤波器，可以实现一种称为“完美重建”（PR）的条件，即当 $X=X^X = \hat{X}$ 时。作为示例使用的四个哈尔小波滤波器属于一类称为“正交小波”的滤波器，其中正交性定义了低通和高通滤波器之间的关系。正交小波始终提供PR。

作者的框架专注于数据集自适应、可学习的离散小波变换，用于对输入到3DGS的图像进行自动的从粗到精频率调制。作者使用了WaveC - Net提供的可微DWT实现，但在第4节和补充材料中额外推导了关于高通滤波器的梯度。

四、方法

图3展示了AutoOpti3DGS框架的概述。一般来说，AutoOpti3DGS将输入图像输入到正向DWT，然后将得到的子带输入到反向DWT以重建图像。这代表了一种操纵输入图像的方式，从而实现高斯优化表示。

关于从粗到精的调制，当输入图像失去高频时就实现了“粗”的部分。这可以简单地通过将高通滤波器初始化为零来实现，这也会导致除 $LL$ 之外的所有子带都为零矩阵。如图3所示，这些子带最初完全是黑色的。

为了逐渐且自动地引入高频分量，从而完成从粗到精调制的“细”部分，高通滤波器必须是可学习的并适应图像。因此，额外推导了关于公式（2）中高通分析矩阵的梯度 $∂L∂H0\frac{\partial L}{\partial H_0}$ 和 $∂L∂H1\frac{\partial L}{\partial H_1}$ ：
$\begin{cases} \frac{\partial L}{\partial H_0} = \frac{\partial L}{\partial X_{LH}} \frac{\partial X_{LH}}{\partial H_0} + \frac{\partial L}{\partial X_{HH}} \frac{\partial X_{HH}}{\partial H_0} = \frac{\partial L}{\partial X_{LH}} L^{\top}_1 X^{\top} + \frac{\partial L}{\partial X_{HH}} H^{\top}_1 X^{\top} \\ \frac{\partial L}{\partial H_1} = \frac{\partial L}{\partial X_{HL}} \frac{\partial X_{HL}}{\partial H_1} + \frac{\partial L}{\partial X_{HH}} \frac{\partial X_{HH}}{\partial H_1} = X^T L^T_0 \frac{\partial L}{\partial X_{HL}} + X^T H^T_0 \frac{\partial L}{\partial X_{HH}} \end{cases}$
高通合成矩阵可以以类似的方式学习。在补充材料中，作者进行了对比研究，表明学习高通分析或合成滤波器都能实现稳定的频率调制。为了保留 $LL$ 子带提供的粗略和基础结构，作者不尝试学习低通滤波器。相比之下，学习高通滤波器风险较小，因为它们主要捕获不会在结构上产生干扰的精细细节。

为了优化高通滤波器，引入了以下辅助小波损失：
$Lwavelet=∑(⋅)∈{0,1}∥H(⋅)−H(⋅)ref∥22L_{wavelet} = \sum_{(·) \in \{0, 1\}} \|H_{(·)} - H^{ref}_{(·)}\|^2_2$
其中 $\in \{0, 1\}$ 表示垂直或水平滤波维度， $H_{(·)}$ 表示正在学习的高通分析矩阵。 $H^{ref}_{(·)}$ 是用于完美重建图像的参考，即具有所有精细细节。这个参考是基于第3节中引入的哈尔1D高通滤波器构建的。因此，垂直滤波的高通分析参考矩阵 $H0refH^{ref}_0$ 为：
$H0ref=[−1212000⋯00−12120⋯0000−12⋯⋯⋯⋯⋯⋯⋯⋯⋯]H^{ref}_0 = \begin{bmatrix} -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 & 0 & \cdots & 0 \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & \cdots & 0 & 0 \\ 0 & 0 & -\frac{1}{\sqrt{2}} & \cdots & & & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{bmatrix}$
$H1refH^{ref}_1$ 类似，只是将其1D滤波器沿列移动。由于这些参考是由正交小波构建的，可学习高通滤波器向其参考的收敛意味着向PR条件的收敛，此时高频变得可用，标志着从粗到精策略的结束。注意哈尔参考滤波器只有两个系数，在低通情况下完全对称，在高通情况下反对称。因此，虽然从技术上讲可以使用任何类型、任何系数数量的滤波器，但类似哈尔的滤波器最容易优化。请参考图3的“渐进高频学习”部分，以查看随着训练进行更精细细节的出现。

小波损失 $L_{wavelet}$ 使用以下项进行平衡：
$λH=∥X^HH−XHHgt∥1∥XHHgt∥1+ϵ\lambda_H = \frac{\|\hat{X}_{HH} - X^{gt}_{HH}\|_1}{\|X^{gt}_{HH}\|_1 + \epsilon}$
它根据渲染图像的高频（ $X^HH\hat{X}_{HH}$ ）与原始精细图像的高频（ $XHHgtX^{gt}_{HH}$ ）的偏离程度来权衡其重要性。在训练早期， $HH$ 差异较大，导致高通矩阵快速趋向于哈尔参考，而在训练后期则相反。 $ϵ\epsilon$ 是一个极小的浮点数，以防止除零。AutoOpti3DGS的总损失如下：
$L_{3DGS} + \lambda_H L_{wavelet}$
总之，AutoOpti3DGS通过从粗图像开始实现高斯数量的减少，粗图像是由于高通滤波器初始化为零而产生的。粗图像对应于粗高斯，因为几乎没有精细细节需要将它们分裂。辅助损失促使滤波器趋向于其参考，从而允许更精细的细节或细高斯出现。与从头到尾的全频谱训练相比，这优化了高斯数量，因为在这种情况下，相对均匀的区域可能由密集的细高斯集表示，而不是由稀疏的粗高斯集有效地表示。请参考图1以获取此视觉示例。

五、实验

5.1 数据集与实现细节

AutoOpti3DGS在使用3个输入视图的LLFF数据集和使用12个输入视图的Mip - NeRF 360数据集上进行评估。这些基准数据集包含多个对象或场景的多视图图像。3DGS的新视图合成能力在一些训练期间从未见过的保留测试图像上进行测试。

为了评估渲染质量，作者使用PSNR、SSIM和LPIPS作为评估指标。第一个指标测量逐像素差异，而另外两个测量感知相似性。为了量化高斯优化，作者跟踪训练期间高斯的峰值数量，对每个数据集中的所有场景进行平均。此外，作者还报告训练时间，同样对各场景进行平均。

与Vanilla 3DGS和Opti3DGS进行比较，这三种方法都采用了Drop - Gaussian策略，该策略在训练期间随机丢弃高斯，以在稀疏视图场景中获得更好的泛化能力。此外，它们都训练10K次迭代。对于Opti3DGS，在迭代范围0 - 1K、1 - 2K、2 - 3K和3 - 4K时分别使用窗口大小为15、9、5和3的均值滤波器进行模糊处理。4K次迭代后不使用模糊。这些设置遵循原始Opti3DGS配置。相比之下，AutoOpti3DGS只需要设置高通滤波器的学习率，设置为 $1 e - 3$ 。

除了Vanilla 3DGS，Opti3DGS和AutoOpti3DGS都集成到高效的3DGS变体中，以进一步减少高斯数量。具体来说，作者采用Mini - Splatting和Compact - 3DGS作为基础框架，以展示AutoOpti3DGS的互补有效性。所有实验都在具有16GB内存的GeForce RTX 4070 Ti Super GPU上进行。

5.2 定量与定性结果

表1和表2总结了定量结果。在表1中，在3DGS和两个高效框架中，Opti3DGS中使用的固定模糊时间表对LLFF数据集适应性不佳，导致PSNR下降约0.8 - 1.0，尽管高斯数量减少了约10 - 15%。相比之下，AutoOpti3DGS在将高斯数量减少约18 - 23%的同时，保持了与3DGS相当的渲染质量。这种改进带来了一些可忽略不计的训练时间增加，这归因于在每次训练迭代中使用DWT，但这可能可以通过使用延迟正则化来缓解，在延迟正则化中，滤波器更新仅每隔几次迭代执行一次。图4展示了新视图的定性结果。

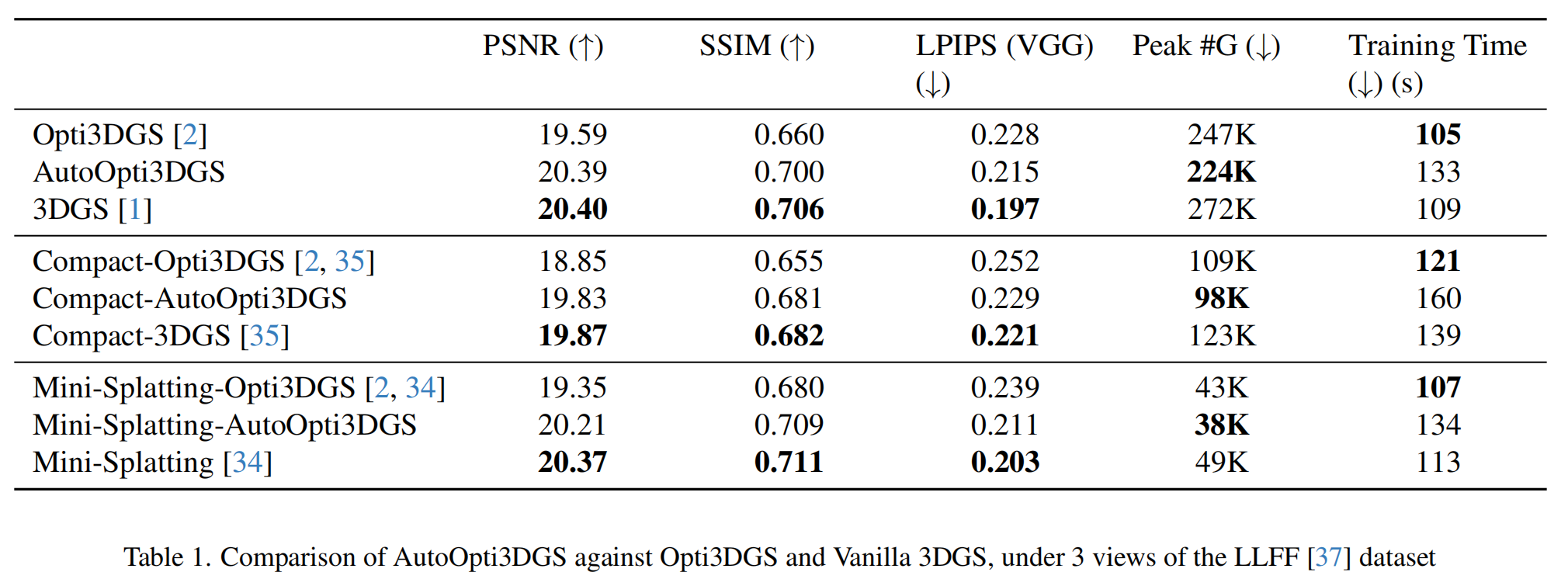
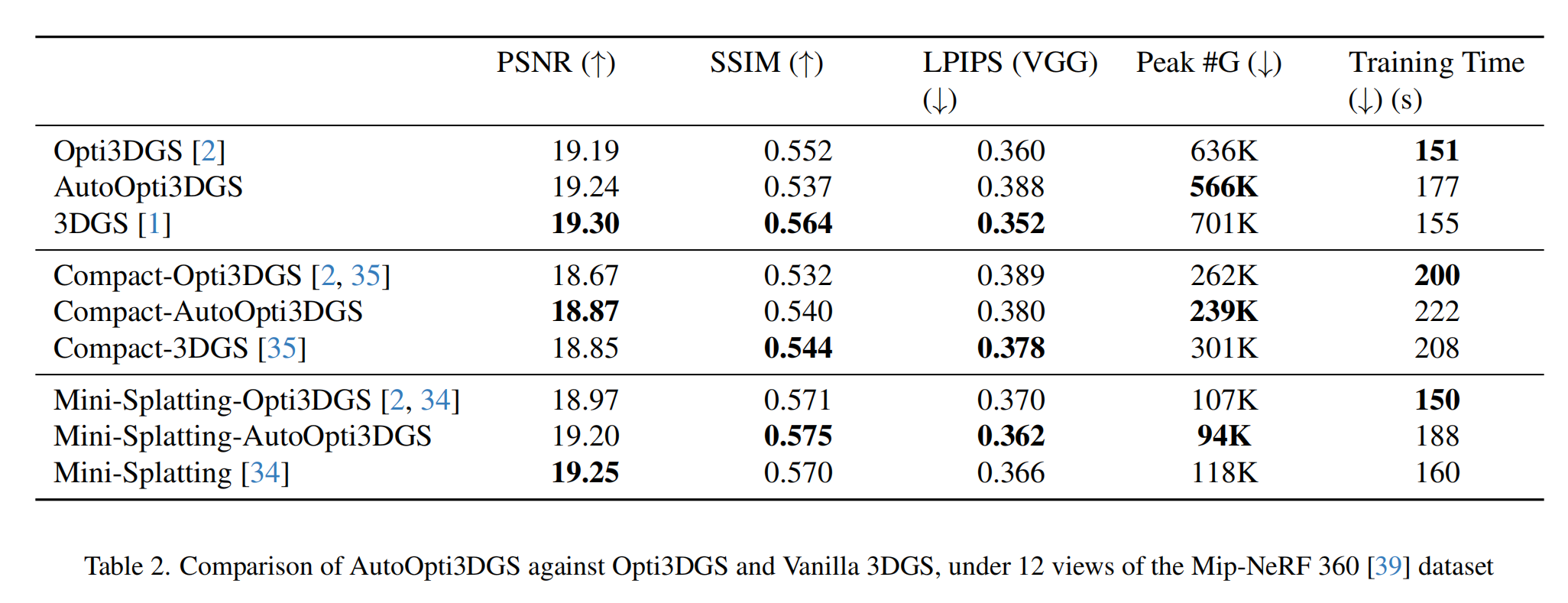
在表2中，Opti3DGS的模糊设置在Mip - NeRF 360数据集上表现有效，在减少高斯使用的同时提供与3DGS相当的渲染质量。AutoOpti3DGS实现了同样具有竞争力的性能，同时进一步减少了高斯数量。

5.3 对比研究

此对比研究展示了PR收敛对作者的AutoOpti3DGS框架的相对重要性。可学习高通滤波器的目标是具有单位 $ℓ2\ell_2$ 范数的正交哈尔滤波器，由于其可学习性质，该约束已被放宽。为了重新引入 $ℓ2\ell_2$ 范数约束并使可学习滤波器更“像小波”，将以下损失添加到训练目标中：
$norm(∥H(⋅)∥22−1)L_{wavelet \ norm} = \sum_{(·) \in \{0, 1\}} \lambda_{H \ norm} (\|H_{(·)}\|^2_2 - 1)$
其中 $norm\lambda_{H \ norm}$ 通过实验设置为0.01，以与其他训练目标平衡。范数损失仅在5K次迭代后应用，以防止高通滤波器过快收敛到单位范数参考，这将违背从粗到精的目的。

结果显示在表3中。添加 $L_{wavelet \ norm}$ 有助于可学习滤波器更接近其正交参考并更接近重建原始图像。如图5左侧所示，使用 $L_{wavelet \ norm}$ 的最终滤波器为 $[- 0.6062, 0.6061]$ ，不使用它的最终滤波器为 $[- 0.5029, 0.5027]$ （此处的滤波器值是可学习矩阵各行的平均值）。前者比后者更接近哈尔滤波器，因此更接近PR。

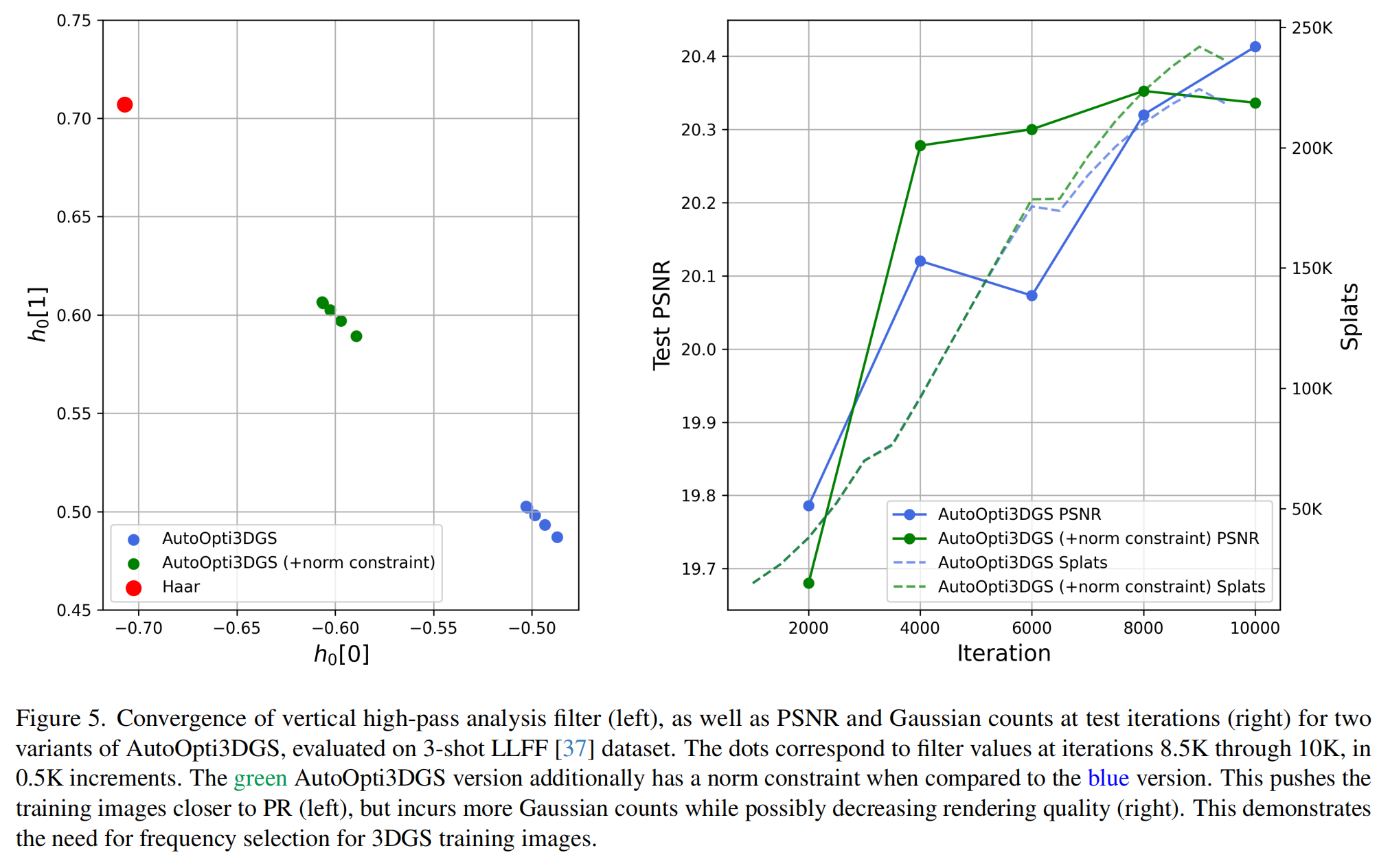
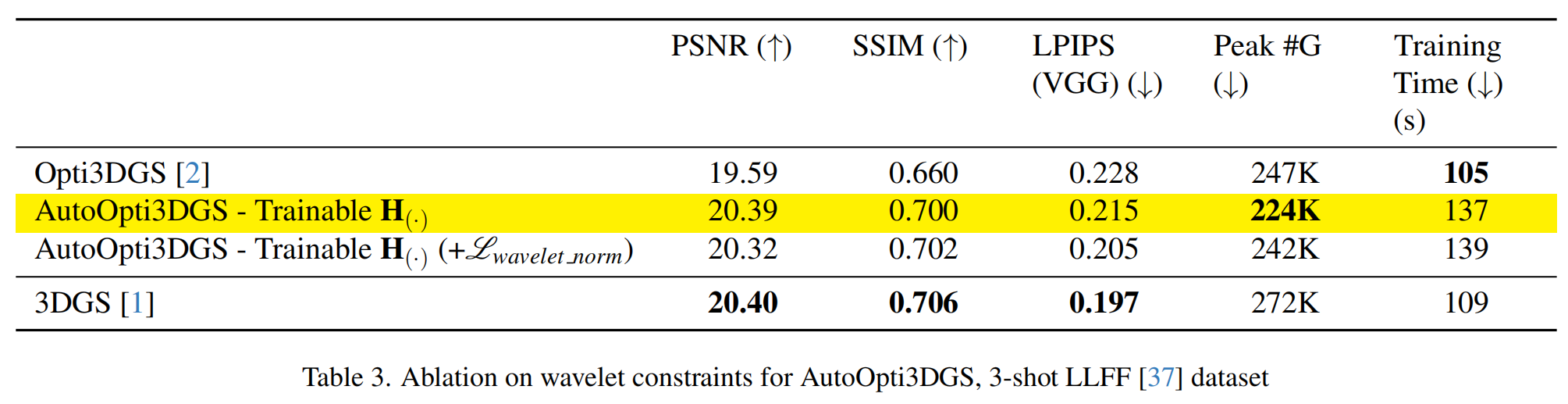
然而，这并没有带来明显的渲染质量提升，同时需要更大的高斯数量，如图5右侧所示。这表明，在某些时候，高频不再有益。此外，对于高斯数量而言，存在比原始输入图像更有效的表示。可学习DWT有效地学习了这种表示。关于是否学习高通分析或合成滤波器的另一个对比研究，请参考补充材料。

六、结论

在本文中，作者提出了AutoOpti3DGS框架，旨在在保持渲染质量的同时减少高斯基元的数量。作者的框架通过在输入图像级别实施从粗到精的策略来实现这一点，该策略在训练期间延迟了细高斯的出现。通过将早期阶段的监督限制在低频内容上，AutoOpti3DGS防止模型过早引入过于精细或冗余的高斯。这是通过正向和反向离散小波变换（DWT）实现的，其中高通滤波器初始化为零，并通过训练逐渐激活。辅助损失将其引导向正交参考，从而实现精细细节的渐进重建。结果，AutoOpti3DGS消除了手动定义模糊参数的需要，只需要设置小波学习率。在LLFF和Mip - NeRF 360数据集上的实验表明，AutoOpti3DGS在减少高斯数量的同时保持了有竞争力的渲染质量。此外，它很容易与其他高效的3DGS框架互补，因为输入图像处理不需要重大改变。

未来工作：首先，如第5节所述，作者旨在将延迟正则化纳入滤波器更新，以免增加额外的训练时间，这意味着PR收敛将需要更长时间。作者认为这不会影响从粗到精策略在减少高斯数量方面的好处。其次，调制策略可以自然地扩展到多级DWT，其中单级的 $LL$ 子带被递归分解，以产生逐渐更粗的表示。当反向DWT使用2级 $LL$ 子带作为唯一的非零输入时，得到的重建图像甚至会比使用1级 $LL$ 时更粗。作者相信这种扩展有很大的潜力进一步减少高斯数量，因为它扩展了从粗到精调制的范围。此外，可以设计一种学习机制，用于自动从高到低切换DWT级别。尽管如此，在没有激进模糊的情况下，AutoOpti3DGS在减少高斯数量方面始终优于Opti3DGS，特别是当后者从使用大窗口大小（15）的均值滤波的重度模糊图像输入开始时。

声明

本文内容为论文学习收获分享，受限于知识能力，本文对原文的理解可能存在偏差，最终内容以原论文为准。本文信息旨在传播和学术交流，其内容由作者负责，不代表本号观点。文中作品文字、图片等如涉及内容、版权和其他问题，请及时与我们联系，我们将在第一时间回复并处理。

ICCV 2025|从粗到细：用于高效3D高斯溅射的可学习离散小波变换