基础算法模板

基础排序算法-快速排序

数据范围$10^5$， 算法时间复杂度$O(n\log n)$

#include <iostream>

using namespace std;

const int N = 1e5 + 10;
int n, w[N];

void quick_sort(int l, int r) {
    if (l >= r) return;
    
    int val = w[l + r >> 1];
    int p1 = l - 1, p2 = r + 1;
    while (p1 < p2) {
        while (w[++p1] < val);
        while (w[--p2] > val);
        if (p1 < p2) swap(w[p1], w[p2]);
    }
    
    quick_sort(l, p2);
    quick_sort(p2 + 1, r);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    
    quick_sort(1, n);
    
    for (int i = 1; i <= n; ++i) cout << w[i] << ' ';
    cout << '\n';
    
    return 0;
}

基础排序算法-第K个数

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, k, w[N];

void quick_sort(int l, int r) {
    if (l >= r) return;
    int val = w[l + r >> 1];
    int p1 = l - 1, p2 = r + 1;
    while (p1 < p2) {
        while (w[++p1] < val);
        while (w[--p2] > val);
        if (p1 < p2) swap(w[p1], w[p2]);
    }
    
    quick_sort(l, p2);
    quick_sort(p2 + 1, r);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> k;
    for (int i = 1; i <= n; ++i) cin >> w[i];

    quick_sort(1, n);

    cout << w[k] << '\n';

    return 0;
}

基础排序算法-归并排序

先递归再合并, 简单的写法是自上而下的进行递归划分, 递归到最后一层, 开始合并, 向上递归最后完成排序, 算法时间复杂度$O(n\log n)$, 空间相较于快速排序需要新增一个临时数组存储每次排序后的结果

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, w[N], tmp[N];

void merge_sort(int l, int r) {
     if (l >= r) return;
     int mid = l + r >> 1;
     merge_sort(l, mid), merge_sort(mid + 1, r);

     int p1 = l, p2 = mid + 1, k = 0;
     while (p1 <= mid && p2 <= r) {
         if (w[p1] <= w[p2]) tmp[k++] = w[p1++];
         else tmp[k++] = w[p2++];
     }

     while (p1 <= mid) tmp[k++] = w[p1++];
     while (p2 <= r) tmp[k++] = w[p2++];

     for (int i = l; i <= r; ++i) w[i] = tmp[i - l];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;
    for (int i = 0; i < n; ++i) cin >> w[i];

    merge_sort(0, n - 1);
    
    for (int i = 0; i < n; ++i) cout << w[i] << ' ';
    cout << '\n';

    return 0;
}

基础排序算法-归并排序求逆序对的数量

统计逆序对的算法核心是归并排序过程中自下而上的 合并有序的两段, 如果当前w[p1] > w[p2], 那么从mid + 1到p2与w[p1]构成逆序对, 或者p1到mid与w[p2]构成逆序对

#include <iostream>

using namespace std;

typedef long long LL;
const int N = 1e5 + 10;

int n, w[N], tmp[N];
LL cnt = 0;

void merge_sort(int l, int r) {
     if (l >= r) return;
     int mid = l + r >> 1;
     merge_sort(l, mid), merge_sort(mid + 1, r);

     int p1 = l, p2 = mid + 1, k = 0;
     while (p1 <= mid && p2 <= r) {
         if (w[p1] <= w[p2]) tmp[k++] = w[p1++];
         else {
             cnt += mid - p1 + 1;
             tmp[k++] = w[p2++];
         }
     }

     while (p1 <= mid) tmp[k++] = w[p1++];
     while (p2 <= r) tmp[k++] = w[p2++];

     for (int i = l; i <= r; ++i) w[i] = tmp[i - l];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;
    for (int i = 0; i < n; ++i) cin >> w[i];

    merge_sort(0, n - 1);

    cout << cnt << '\n';
    return 0;
}

基础二分算法-整数二分

对于含有相同数的一组有序序列查询左端点和右端点, 可以根据二分的原理进行查询小于等于val的位置, 第一个大于等于val的位置, 对应C++语言当中就是lower_bound和upper_bound

#include <iostream>

using namespace std;

const int N = 1e5 + 10, M = 1e4 + 10;

int n, q;
int w[N];

//找到右边界该位置左侧包括该位置都小于等于val
int find_right(int val) {
    int l = 0, r = n - 1;
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (w[mid] <= val) l = mid;
        else r = mid - 1;
    }
    return l;
}

//找到左边界该位置包括该位置左侧都是小于等于val
int find_left(int val) {
    int l = 0, r = n - 1;
    while (l < r) {
        int mid = l + r >> 1;
        if (w[mid] >= val) r = mid;
        else l = mid + 1;
    }
    return r;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> q;
    for (int i = 0; i < n; ++i) cin >> w[i];

    while (q--) {
        int val;
        cin >> val;
        int l = find_left(val), r = find_right(val);
        if (w[l] != val || w[r] != val) cout << -1 << ' ' << -1 << '\n';
        else cout << l << ' ' << r << '\n';
    }

    return 0;
}

基础二分算法-小数二分

#include <iostream>

using namespace std;

const double EPS = 1e-8;
double val;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> val;
    
    double l = -10010, r = 10000;
    while (abs(l - r) > EPS) {
        double mid = (l + r) / 2;
        if (mid * mid * mid <= val) l = mid;
        else r = mid;
    }

    printf("%.6lf\n", l);

    return 0;
}

高精度算法-高精度加法

#include <iostream>
#include <vector>

using namespace std;

vector<int> res;

void calc_add(vector<int> &d1, vector<int> &d2) {
    if (d1.size() < d2.size()) {
        calc_add(d2, d1);
        return;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
         c += d1[i];
         if (i < d2.size()) c += d2[i];
         res.push_back(c % 10);
         c /= 10;
    }

    if (c) res.push_back(c);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    string s1, s2;
    vector<int> d1, d2;

    cin >> s1 >> s2;
    for (int i = s1.size() - 1; i >= 0; --i) d1.push_back(s1[i] - '0');
    for (int i = s2.size() - 1; i >= 0; --i) d2.push_back(s2[i] - '0');

    calc_add(d1, d2);

    for (int i = res.size() - 1; i >= 0; --i) cout << res[i];
    cout << '\n';

    return 0;
}

高精度算法-高精度减法

#include <iostream>
#include <vector>

using namespace std;

vector<int> res;

void calc_add(vector<int> &d1, vector<int> &d2) {
    if (d1.size() < d2.size()) {
        calc_add(d2, d1);
        return;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
         c += d1[i];
         if (i < d2.size()) c += d2[i];
         res.push_back(c % 10);
         c /= 10;
    }

    if (c) res.push_back(c);
}

bool cmp(vector<int> &d1, vector<int> &d2) {
    if (d1.size() != d2.size()) return d1.size() >= d2.size();
    for (int i = d1.size() - 1; i >= 0; --i) {
        if (d1[i] != d2[i]) return d1[i] >= d2[i];
    }
    return true;
}

bool calc_sub(vector<int> &d1, vector<int> &d2) {
    if (!cmp(d1, d2)) {
        calc_sub(d2, d1);
        return false;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
        int val = d1[i] - c;
        if (i < d2.size()) val -= d2[i];
        if (val < 0) {
            val = (val + 10) % 10;
            c = 1;
        }
        else c = 0;
        res.push_back(val);
    }

    while (res.size() > 1 && res.back() == 0) res.pop_back();

    return true;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    string s1, s2;
    vector<int> d1, d2;

    cin >> s1 >> s2;
    for (int i = s1.size() - 1; i >= 0; --i) d1.push_back(s1[i] - '0');
    for (int i = s2.size() - 1; i >= 0; --i) d2.push_back(s2[i] - '0');

    if (!calc_sub(d1, d2)) cout << '-';
    for (int i = res.size() - 1; i >= 0; --i) cout << res[i];
    cout << '\n';

    return 0;
}

高精度算法-高精度乘法

高精度乘法一般用于一个高精度数字×正常大小的数字, 计算结果是高精度数字

#include <iostream>
#include <vector>

using namespace std;

vector<int> res;

void calc_add(vector<int> &d1, vector<int> &d2) {
    if (d1.size() < d2.size()) {
        calc_add(d2, d1);
        return;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
         c += d1[i];
         if (i < d2.size()) c += d2[i];
         res.push_back(c % 10);
         c /= 10;
    }

    if (c) res.push_back(c);
}

bool cmp(vector<int> &d1, vector<int> &d2) {
    if (d1.size() != d2.size()) return d1.size() >= d2.size();
    for (int i = d1.size() - 1; i >= 0; --i) {
        if (d1[i] != d2[i]) return d1[i] >= d2[i];
    }
    return true;
}

bool calc_sub(vector<int> &d1, vector<int> &d2) {
    if (!cmp(d1, d2)) {
        calc_sub(d2, d1);
        return false;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
        int val = d1[i] - c;
        if (i < d2.size()) val -= d2[i];
        if (val < 0) {
            val = (val + 10) % 10;
            c = 1;
        }
        else c = 0;
        res.push_back(val);
    }

    while (res.size() > 1 && res.back() == 0) res.pop_back();

    return true;
}

void calc_mul(vector<int> &d, int val) {
    res.clear();
    int c = 0;
    for (int i = 0; i < d.size(); ++i) {
        c += d[i] * val;
        res.push_back(c % 10);
        c /= 10;
    }
    if (c) res.push_back(c);
    while (res.size() > 1 && res.back() == 0) res.pop_back();
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    vector<int> d1, d2;
    
    string s;
    int val;
    cin >> s >> val;
    for (int i = s.size() - 1; i >= 0; --i) d1.push_back(s[i] - '0');
    
    calc_mul(d1, val);
    for (int i = res.size() - 1; i >= 0; --i) cout << res[i];
    cout << '\n';

    return 0;
}

高精度算法-高精度除法

高精度除法一般是一个高精度数字除以一个正常int数字, 计算结果一般是高精度数字和余数

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

vector<int> res;

void calc_add(vector<int> &d1, vector<int> &d2) {
    if (d1.size() < d2.size()) {
        calc_add(d2, d1);
        return;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
         c += d1[i];
         if (i < d2.size()) c += d2[i];
         res.push_back(c % 10);
         c /= 10;
    }

    if (c) res.push_back(c);
}

bool cmp(vector<int> &d1, vector<int> &d2) {
    if (d1.size() != d2.size()) return d1.size() >= d2.size();
    for (int i = d1.size() - 1; i >= 0; --i) {
        if (d1[i] != d2[i]) return d1[i] >= d2[i];
    }
    return true;
}

bool calc_sub(vector<int> &d1, vector<int> &d2) {
    if (!cmp(d1, d2)) {
        calc_sub(d2, d1);
        return false;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
        int val = d1[i] - c;
        if (i < d2.size()) val -= d2[i];
        if (val < 0) {
            val = (val + 10) % 10;
            c = 1;
        }
        else c = 0;
        res.push_back(val);
    }

    while (res.size() > 1 && res.back() == 0) res.pop_back();

    return true;
}

void calc_mul(vector<int> &d, int val) {
    res.clear();
    int c = 0;
    for (int i = 0; i < d.size(); ++i) {
        c += d[i] * val;
        res.push_back(c % 10);
        c /= 10;
    }
    if (c) res.push_back(c);
    while (res.size() > 1 && res.back() == 0) res.pop_back();
}

void calc_div(vector<int> &d, int val, int &r) {
    res.clear();
    r = 0;
    for (int i = d.size() - 1; i >= 0; --i) {
        r = r * 10 + d[i];
        res.push_back(r / val);
        r %= val;
    }
    reverse(res.begin(), res.end());
    while (res.size() > 1 && res.back() == 0) res.pop_back();
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    vector<int> d1, d2;

    string s;
    int val;
    cin >> s >> val;
    for (int i = s.size() - 1; i >= 0; --i) d1.push_back(s[i] - '0');

    int r;
    calc_div(d1, val, r);
    
    for (int i = res.size() - 1; i >= 0; --i) cout << res[i];
    cout << '\n';
    cout << r << '\n';

    return 0;
}

高精度算法模板

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

vector<int> res;

void calc_add(vector<int> &d1, vector<int> &d2) {
    if (d1.size() < d2.size()) {
        calc_add(d2, d1);
        return;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
         c += d1[i];
         if (i < d2.size()) c += d2[i];
         res.push_back(c % 10);
         c /= 10;
    }

    if (c) res.push_back(c);
}

bool cmp(vector<int> &d1, vector<int> &d2) {
    if (d1.size() != d2.size()) return d1.size() >= d2.size();
    for (int i = d1.size() - 1; i >= 0; --i) {
        if (d1[i] != d2[i]) return d1[i] >= d2[i];
    }
    return true;
}

bool calc_sub(vector<int> &d1, vector<int> &d2) {
    if (!cmp(d1, d2)) {
        calc_sub(d2, d1);
        return false;
    }

    res.clear();
    int c = 0;
    for (int i = 0; i < d1.size(); ++i) {
        int val = d1[i] - c;
        if (i < d2.size()) val -= d2[i];
        if (val < 0) {
            val = (val + 10) % 10;
            c = 1;
        }
        else c = 0;
        res.push_back(val);
    }

    while (res.size() > 1 && res.back() == 0) res.pop_back();

    return true;
}

void calc_mul(vector<int> &d, int val) {
    res.clear();
    int c = 0;
    for (int i = 0; i < d.size(); ++i) {
        c += d[i] * val;
        res.push_back(c % 10);
        c /= 10;
    }
    if (c) res.push_back(c);
    while (res.size() > 1 && res.back() == 0) res.pop_back();
}

void calc_div(vector<int> &d, int val, int &r) {
    res.clear();
    r = 0;
    for (int i = d.size() - 1; i >= 0; --i) {
        r = r * 10 + d[i];
        res.push_back(r / val);
        r %= val;
    }
    reverse(res.begin(), res.end());
    while (res.size() > 1 && res.back() == 0) res.pop_back();
}

前缀和差分基本思想

基础前缀和

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int w[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    for (int i = 1; i <= n; ++i) w[i] += w[i - 1];

    while (m--) {
        int l, r;
        cin >> l >> r;
        cout << w[r] - w[l - 1] << '\n';
    }
    return 0;
}

二维前缀和

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int w[N][N], s[N][N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m >> q;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            cin >> w[i][j];
        }
    }

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + w[i][j];
        }
    }

    while (q--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        int ans = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
        cout << ans << '\n';
    }

    return 0;
}

基础差分

先将原来的数组转化为差分数组, 对差分数组进行操作, 然后再求前缀和, 相当于标记对原数组产生了修改作用

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n, m;
int w[N], d[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    for (int i = 1; i <= n; ++i) d[i] = w[i] - w[i - 1];

    while (m--) {
        int l, r, val;
        cin >> l >> r >> val;
        d[l] += val;
        d[r + 1] -= val;
    }

    for (int i = 1; i <= n; ++i) d[i] += d[i - 1];
    for (int i = 1; i <= n; ++i) cout << d[i] << ' ';
    cout << '\n';
    return 0;
}

二维差分

将原数组的数据插入到差分二维数组中, 也就是将原数组看作是前缀和, 将原数组进行拆分, 最后对整个差分数组求前缀和, 结果就是原数组修改后的值

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int d[N][N], s[N][N];

void insert(int x1, int y1, int x2, int y2, int val) {
    d[x1][y1] += val;
    d[x2 + 1][y1] -= val;
    d[x1][y2 + 1] -= val;
    d[x2 + 1][y2 + 1] += val;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m >> q;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            int val;
            cin >> val;
            insert(i, j, i, j, val);
        }
    }

    while (q--) {
        int x1, y1, x2, y2, val;
        cin >> x1 >> y1 >> x2 >> y2 >> val;
        insert(x1, y1, x2, y2, val);
    }

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + d[i][j];
        }
    }

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            cout << s[i][j] << ' ';
        }
        cout << '\n';
    }

    return 0;
}

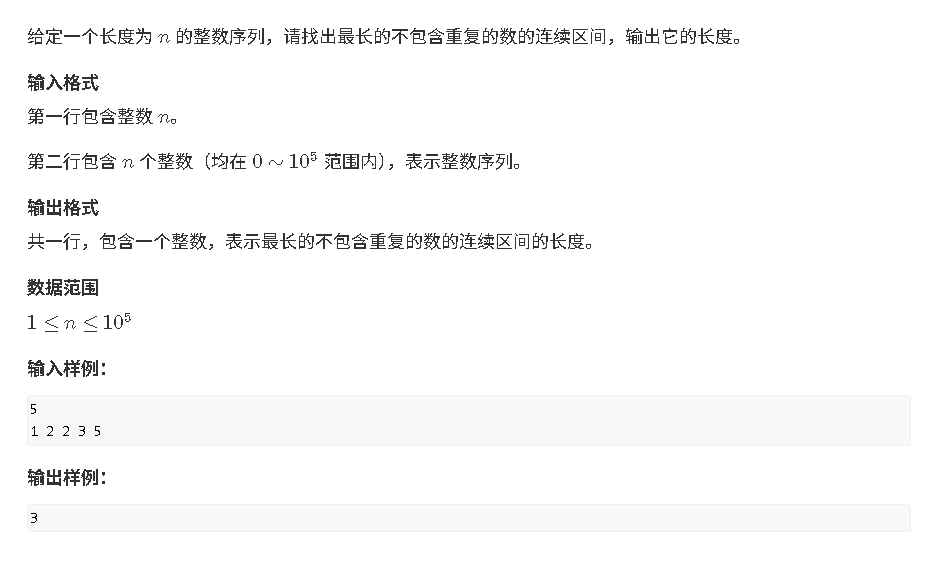
基础双指针算法

最长连续不重复子数组

#include <iostream>
#include <set>

using namespace std;

const int N = 1e5 + 10;

int n, w[N], cnt[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n;
    for (int i = 0; i < n; ++i) cin >> w[i];

    int l = 0, res = 1;
    cnt[w[l]]++;
    
    for (int r = 1; r < n; ++r) {
        cnt[w[r]]++;
        while (l < r && cnt[w[r]] > 1) {
            cnt[w[l]]--;
            l++;
        }
        res = max(res, r - l + 1);
    }

    cout << res << '\n';

    return 0;
}

判断子序列

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m, a[N], b[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m;
    for (int i = 0; i < n; ++i) cin >> a[i];
    for (int i = 0; i < m; ++i) cin >> b[i];

    int i = 0, j = 0;
    while (i < n && j < m) {
        if (a[i] != b[j]) j++;
        else i++, j++;
    }

    if (i == n) cout << "Yes" << '\n';
    else cout << "No" << '\n';

    return 0;
}

数组元素的目标和

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m, x;
int a[N], b[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n >> m >> x;
    for (int i = 0; i < n; ++i) cin >> a[i];
    for (int i = 0; i < m; ++i) cin >> b[i];

    int i = 0, j = m - 1;
    while (i < n && j > 0) {
        int val = a[i] + b[j];
        if (val > x) j--;
        else if (val < x) i++;
        else break;
    }

    if (a[i] + b[j] != x) {
        i = n - 1, j = 0;
        while (i > 0 && j < m) {
            int val = a[i] + b[j];
            if (val > x) i--;
            else if (val < x) j++;
            else break;
        }
    }
    
    cout << i << ' ' << j << '\n';
    return 0;
}

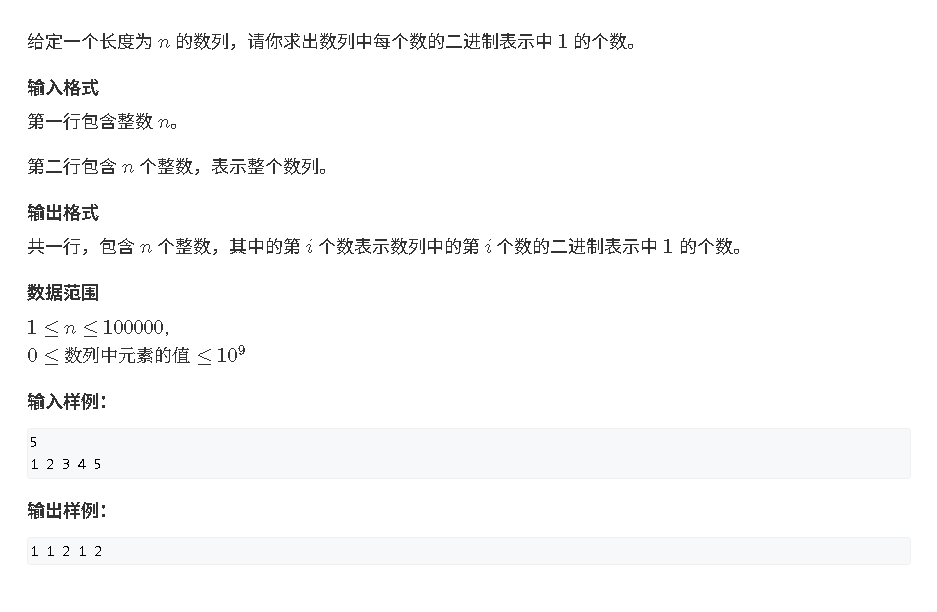
位运算

计算二进制数字当中1的个数

#include <iostream>

using namespace std;

const int N = 30;

int n;

int calc_cnt(int val) {
    int cnt = 0;
    for (int i = 0; i < N; ++i) cnt += val >> i & 1;
    return cnt;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    cin >> n;
    for (int i = 0; i < n; ++i) {
        int val;
        cin >> val;
        cout << calc_cnt(val) << ' ';
    }
    cout << '\n';

    return 0;
}

离散化

因为先进行在每个位置上添加一个数字, 在后面不需要对数字进行更改因此直接离散化后求前缀和即可, 如果添加数字后还要进行修改, 那么需要使用树状数组或者线段树进行解决, 需要进行排序去除重复, 因为插入的次数是$10^5$, 查询的数量是$2\times 10^5$, 最多离散化后的数量$3\times 10^5$

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;
const int N = 3e5 + 10;

int n, m, cnt;
vector<int> d;
vector<PII> insert, q;
int w[N];

int get(int val) {
    int l = 0, r = cnt - 1;
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (d[mid] <= val) l = mid;
        else r = mid - 1;
    }
    return l + 1;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> m;
    for (int i = 0; i < n; ++i) {
        int x, val;
        cin >> x >> val;
        d.push_back(x);
        insert.push_back({x, val});
    }

    for (int i = 0; i < m; ++i) {
        int l, r;
        cin >> l >> r;
        q.push_back({l, r});
        d.push_back(l), d.push_back(r);
    }

    sort(d.begin(), d.end());
    cnt++;
    for (int i = 1; i < d.size(); ++i) {
        if (d[i] != d[i - 1]) d[cnt++] = d[i];
    }

    for (int i = 0; i < n; ++i) {
        auto[x, val] = insert[i];
        x = get(x);
        w[x] += val;
    }

    for (int i = 1; i <= cnt; ++i) w[i] += w[i - 1];

    for (int i = 0; i < m; ++i) {
        auto[l, r] = q[i];
        l = get(l), r = get(r);
        int ans = w[r] - w[l - 1];
        cout << ans << '\n';
    }

    return 0;
}

区间合并

区间合并问题, 一般先按照区间左端点或者右端点进行排序, 排序后对另一个端点进行处理

#include <iostream>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;
const int N = 1e5 + 10;

int n;
PII w[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;
    for (int i = 0; i < n; ++i) {
        int l, r;
        cin >> l >> r;
        w[i] = {l, r};
    }

    sort(w, w + n);

    int res = 1;
    int r = w[0].second;
    for (int i = 1; i < n; ++i) {
        auto[x, y] = w[i];
        if (x <= r && y > r) r = y;
        else if (x > r) {
            r = y;
            res++;
        }
    }
    
    cout << res << '\n';
    return 0;
}