1 问题
训练集训练次数对测试效果的有多大效果,训练次数是否成正相关,是否存在最优训练次数,它的关系图像是怎样的?怎样获得它的关系图像?
2 方法
在这里我们通过torch,数据来自datasets,数据处理使用的是dataloader的分段功能,返回的值通过
correct = (pred.argmax(1)==y).type(torch.int).sum().item()
实现每一组正确的数量,我们在取他们的平均值,在不同训练次数下
得到的平均值不同,我们可以使用两层循~环,第一层对不同次数的训练之后得到i个平均值进行列表展示,第二层对训练集训练进行循环使其进行i次循环,
即 循环多少次返回列表就有多少元素。最后我们进行返回值的可视化。
| 完整代码即注释展示: import torch from torch import nn from torchvision import datasets from torch.utils.data import DataLoader from torchvision.transforms import ToTensor import matplotlib.pyplot as plt import numpy as np plt.rcParams["axes.unicode_minus"] = False # 防止负号显示出错 plt.rcParams['font.family'] = 'SimHei' # (1) 训练集: 训练模型 train_ds = datasets.MNIST( root='data', # 说明数据集下载的路径 download=True, train=True, # 区分训练集还是测试集 transform=ToTensor(), # 尤其需要注意(),将原始数据格式转换为Tensor格式 ) # (2) 测试集: 评估模型的性能/效果 test_ds = datasets.MNIST( root='data', download=True, train=False, transform=ToTensor(), ) # (3) train_loader = DataLoader( dataset=train_ds, batch_size=128, # 每一段的大小是128 shuffle=True, # 1--60000 打乱数据的次序, 一般用于训练 ) # (4) test_loader = DataLoader( dataset=test_ds, batch_size=128 # 测试集不需要shuffle ) # (5) 定义三层全连接网络 # (5.1) 创建一个新的类继承nn.Module class MyNet(nn.Module): # (5.2) 定义网络有哪些层,这些层都作为成员变量 def __init__(self) -> None: super().__init__() self.flatten = nn.Flatten() # 将28x28的图像拉伸为784维向量 # 第1个全连接层Full Connection(FC) # in_features表示该层的前面一层神经元个数 # out_features标识当前这一层神经元个数 # 对应图里面Layer2 self.fc1 = nn.Linear(in_features=784, out_features=512) # 对应Layer3 也是就输出层 self.fc2 = nn.Linear(in_features=512, out_features=10) # (5.3) 定义数据在网络中的流动 # x - 28x28 def forward(self, x): x = self.flatten(x) # 输出: 784, 对应图Layer 1 x = self.fc1(x) # 输出: 512, 对应Layer 2 out = self.fc2(x) # 输出: 10, 对应Layer 3 return out # (6)网络的输入、输出以及测试网络的性能(不经过任何训练的网络) net = MyNet() #网络训练过程 #x,真实标签y ,网络预测标签y_hat #目标:y_hat越来越接近y #算法:mini-batch 梯度下降 #优化器 #具体实现梯度下降法的传播 optimizer=torch.optim.SGD(net.parameters(),lr=1e-3) #损失函数 #衡量y与y_hat之间的差异 loss_fn=nn.CrossEntropyLoss() #训练网络 def train(dataloader,net, loss_fn , optimizer): net.train() #一个batch一个batch的训练网络 for x,y in dataloader: pred=net(x) #衡量y与y_hat之间的loss #y:128,predicate:128x10 crossentropyloss loss=loss_fn(pred,y) #基于loss信息利用优化器从后向前更新网络全部参数<--- optimizer.zero_grad() loss.backward() optimizer.step() #训练一下 list = [] for i in range(20): for j in range(i): train(train_loader,net,loss_fn, optimizer) #todo 简单训练一下后,网络的性能 #网络评估 def test(dataloader ,net ,loss_fn): net.eval() with torch.no_grad(): a = 0 for x,y in dataloader: pred = net(x)#128*10 #当前batch的正确数量 correct = (pred.argmax(1)==y).type(torch.int).sum().item() a = a+int(correct) a = (a//79) return a list.append(test(test_loader, net, loss_fn)) print(list) x=np.array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,8,19]) y = np.array(list) plt.scatter(x,y) plt.title('训练次数对正确率的关系折线图',fontsize = 18) plt.xlabel('训练次数',fontsize = 14) plt.ylabel('正确次数',fontsize = 14) plt.show() |
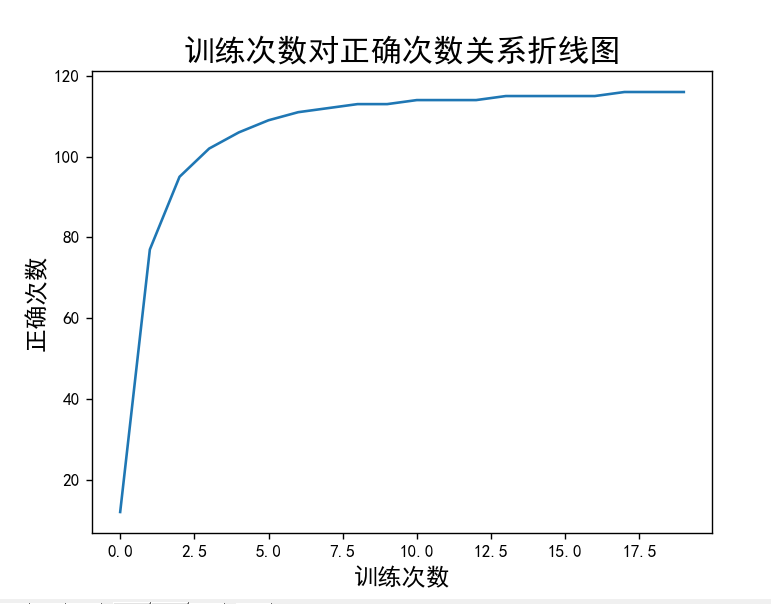
结果图展示:
3 结语
关于训练次数对测试的正确率是否有关这一问题,通过本次实验只能得出训练比起没有进行训练,正确率有非常明显的提高,对于训练次数,训练次数越多正确的越好,同时存在训练效果达到饱和,存在最优训练次数。
本文含有隐藏内容,请 开通VIP 后查看