目录
LeetCode669. 修剪二叉搜索树
链接: 669. 修剪二叉搜索树 - 力扣(LeetCode)
1. 思路
常见误区
直接想法就是:递归处理,然后遇到 root.val < low 或者 root.val > high 的时候直接return NULL,一波修改,赶紧利落。
不难写出如下代码:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr || root->val < low || root->val > high) return nullptr;
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
如果按照以上的代码,遍历到节点0的时候,直接返回none给3的左子树了,最后只剩下返回一个节点3;然而[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的,还要考虑节点0的右子树;因为节点0的右子树可能会符合给的区间【1,3】;我们在重新关注一下第二个示例,如图:
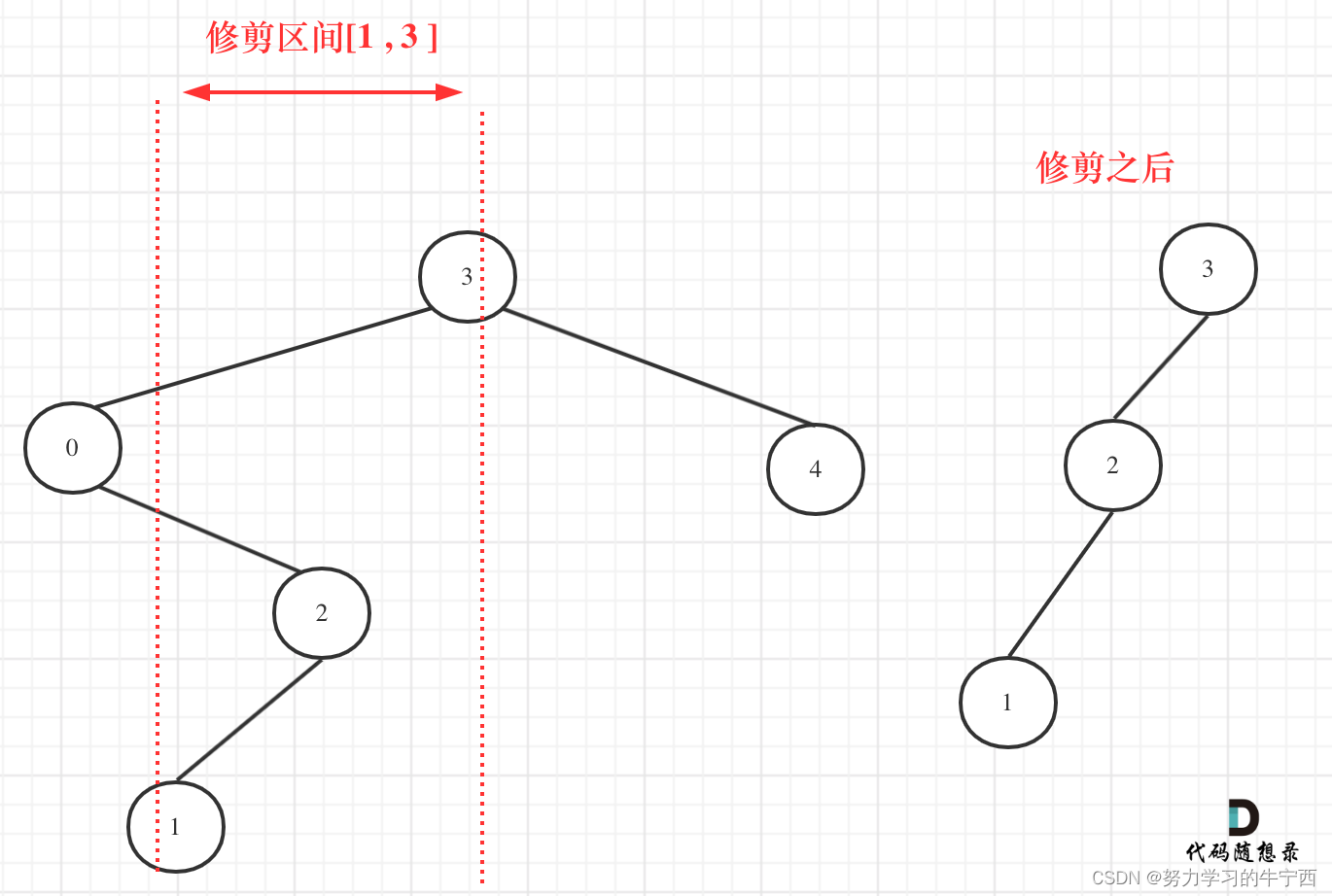
所以以上的代码是不可行的!
应该怎么办?
在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),如图:
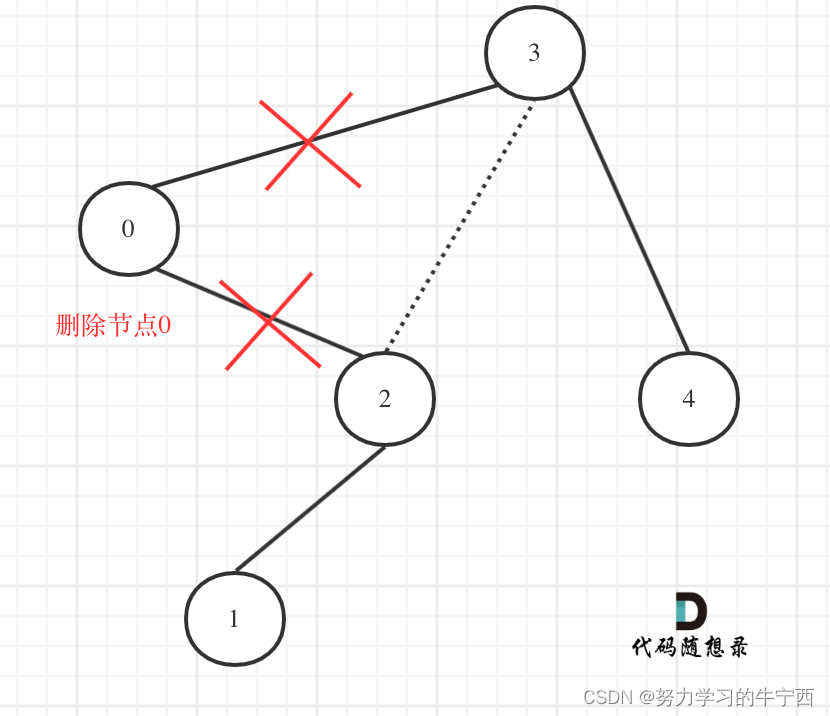
理解了最关键部分了,现在可以开始用递归三部曲写代码了!
2. 代码实现
确定递归函数的参数以及返回值
这里我们为什么需要返回值呢? 因为是要遍历整棵树,做修改,其实不需要返回值也可以,我们也可以完成修剪(其实就是从二叉树中移除节点)的操作。但是有返回值,更方便,可以通过递归函数的返回值来移除节点;
(这个点 在二叉搜索树的插入操作和二叉搜索树的删除操作中已经了解过)
class Solution: def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:确定终止条件
修剪的操作并不是在终止条件上进行的,所以就是遇到空节点返回就可以了
# Base Case if not root: return None确定单层递归的逻辑
- 如果root(当前节点)的元素小于low的数值,那么应该递归右子树,并返回右子树符合条件的头结点;
if root.val < low: return self.trimBST(root.right, low, high)- 如果root(当前节点)的元素大于high的,那么应该递归左子树,并返回左子树符合条件的头结点;
if high < root.val: return self.trimBST(root.left, low, high)- 接下来要将下一层处理完左子树的结果赋给root->left,处理完右子树的结果赋给root->right;最后返回root节点;
if low <= root.val <= high: root.left = self.trimBST(root.left, low, high) root.right = self.trimBST(root.right, low, high) # 返回更新后的剪枝过的当前节点root return root
Example,模拟修剪的过程
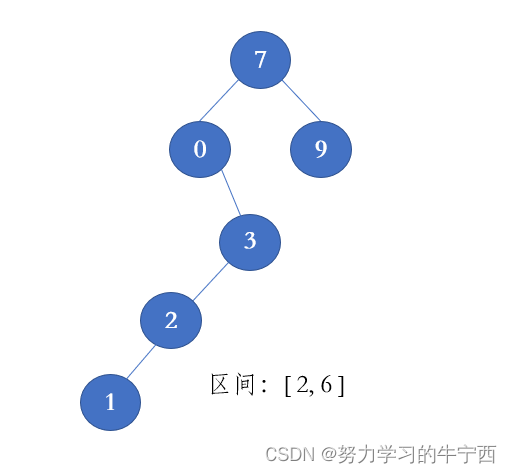
step1. 确定新的root节点;
首先root.val = 7, 大于right=6,所以直接return root.left 节点,而节点0<2 ;所以又直接return 3 节点,现在3 在区间内了,开始处理以节点3为root的子树;
step2. 向下遍历root=3的左右子树,直接作为整个函数的root返回值;
root右子树为空,直接return None,现在开始处理以节点2为root的子树,之后这个处理的返回值,作为3节点的左子树;
step3. 继续向下遍历root= 2的左右子树,返回值为root=3节点的左右子树;
节点2在区间内,继续遍历左右子树,右子树为空直接返回None,左子树为1
step4. 向下遍历root=1的左右子树,返回值为2节点的左子树;
节点1本身就不在范围内,并且小于left=2,直接返回其右子树(为空),作为2的左子树,这样相当于删掉了节点1;
step5. 向上返回,2一个节点为root= 3的左子树,再返回3,整个树只剩3和2了,结束。
整体代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# 递归法
# time:O(N);space:O(N)
class Solution(object):
def trimBST(self, root, low, high):
"""
:type root: TreeNode
:type low: int
:type high: int
:rtype: TreeNode
"""
# base case
if root == None: return None
# 单层递归逻辑
# 先找到合适的root
# 若当前root节点小于左界:只考虑其右子树,用于替代更新后的其本身,抛弃其左子树整体
if root.val < low: return self.trimBST(root.right,low,high)
# 若当前root节点大于右界:只考虑其左子树,用于替代更新后的其本身,抛弃其右子树整体
if root.val > high: return self.trimBST(root.left,low,high)
# 处理root的左右节点
root.left = self.trimBST(root.left,low,high)
root.right = self.trimBST(root.right,low,high)
# 返回更新后的剪枝过的当前节点root
return root枝过的当前节点root
3. 复杂度分析
时间复杂度:O(n)
其中 n 为二叉树的结点数目。
空间复杂度:O(n)
递归栈最坏情况下需要 O(n) 的空间。
4. 思考与收获
迭代解法
因为二叉搜索树的有序性,不需要使用栈模拟递归的过程;在剪枝的时候,可以分为三步:
- 将root移动到[L, R] 范围内,注意是左闭右闭区间
- 剪枝左子树
- 剪枝右子树
代码如下:
# 迭代解法 # time:O(N);space:O(1) class Solution(object): def trimBST(self, root, low, high): """ :type root: TreeNode :type low: int :type high: int :rtype: TreeNode """ if root == None: return None # 先把root调整到区间的位置 while root != None and (root.val < low or root.val > high): if root.val < low: root = root.right elif root.val > high: root = root.left # 此时root已经在区间[low,high] # 处理root的左子树 cur = root while cur != None: while cur.left != None and cur.left.val < low: cur.left = cur.left.right cur = cur.left # 处理root的右子树 cur = root while cur != None: while cur.right != None and cur.right.val >high: cur.right = cur.right.left cur = cur.right return root修剪二叉搜索树递归法,这个思路其实是比较绕的,最终的代码倒是很简洁;如果不对递归有深刻的理解,这道题目还是有难度的!
Reference:代码随想录 (programmercarl.com)
本题学习时间: 90分钟。
LeetCode108.将有序数组转换为二叉搜索树
链接: 108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode)
1. 思路
之前讲过几道构造二叉树类型的题目:
本质上的思路就是寻找分割点,将分割点作为当前节点,然后递归处理左区间和右区间;
题目中说要转换为一棵高度平衡二叉搜索树。为什么强调要平衡呢?
因为只要给我们一个有序数组,如果强调平衡,都可以以线性结构来构造二叉搜索树。例如 有序数组[-10,-3,0,5,9] 可以就可以构造成这样的二叉搜索树,如图。
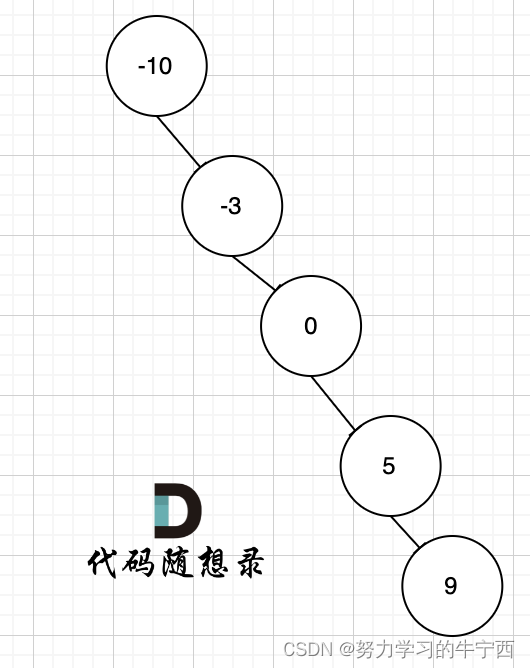
上图中,是符合二叉搜索树的特性吧,如果要这么做的话,是不是本题意义就不大了,所以才强调是平衡二叉搜索树。其实数组构造二叉树,构成平衡树是自然而然的事情,因为大家默认都是从数组中间位置取值作为节点元素,一般不会随机取。所以想构成不平衡的二叉树是自找麻烦。
应该怎么做呢?
我们说过了,本质上的思路就是寻找分割点,将分割点作为当前节点,然后递归处理左区间和右区间;有序数组构造二叉搜索树就比较容易了,分割点就是数组中间的位置;(选中间位置的节点为分割点可以保证左子树右子树数量相等,才可以保持平衡)
那么问题来了,如果数组长度为偶数,中间节点有两个,取哪一个?
取哪一个都可以,只不过构成了不同的平衡二叉搜索树。例如:输入:[-10,-3,0,5,9];如下两棵树,都是这个数组的平衡二叉搜索树:
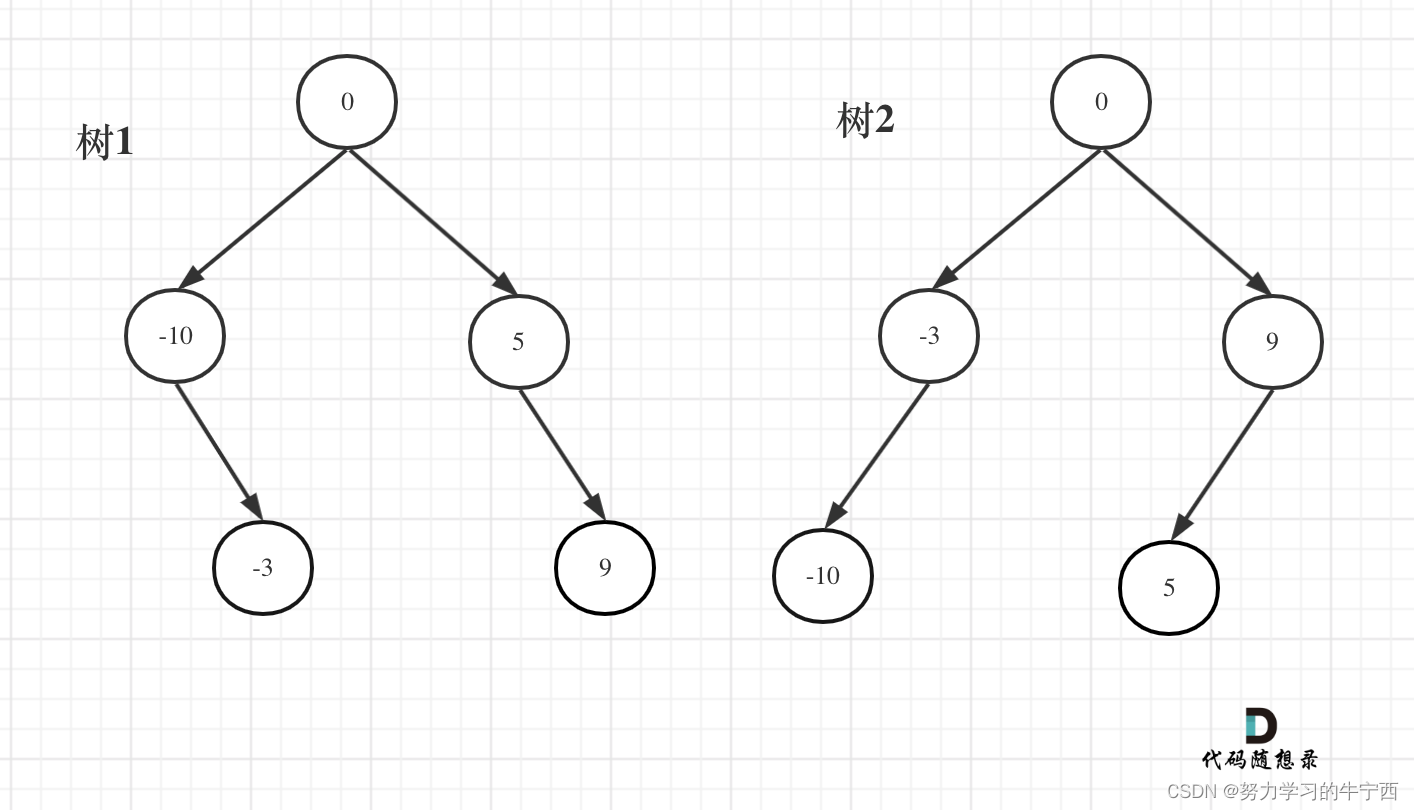
如果要分割的数组长度为偶数的时候,中间元素为两个,是取左边元素 就是树1,取右边元素就是树2。这也是题目中强调答案不是唯一的原因。 理解这一点,这道题目算是理解到位了。
2. 代码实现
递归三部曲
确定递归函数返回值及参数
- 删除二叉树节点,增加二叉树节点,都是用递归函数的返回值来完成,这样是比较方便的。相信大家如果仔细看了**二叉树:搜索树中的插入操作 (opens new window)和二叉树:搜索树中的删除操作 (opens new window)**,一定会对递归函数返回值的作用深有感触。那么本题要构造二叉树,依然用递归函数的返回值来构造中节点的左右孩子。
- 再来看参数,首先是传入数组,然后就是左下标left和右下标right,我们在**二叉树:构造二叉树登场! (opens new window)** 中提过,在构造二叉树的时候尽量不要重新定义左右区间数组,而是用下标来操作原数组。(因为如果重新定义左右区间数组的话,每次都要在新的空间上copy数组,会使得代码效率低下)
class Solution: def sortedArrayToBST(self, nums: List[int]) -> TreeNode: def traversal(self, nums: List[int], left: int, right: int) -> TreeNode:这里注意,我这里定义的是左闭右闭区间,在不断分割的过程中,也会坚持左闭右闭的区间,这又涉及到我们讲过的循环不变量。
在**二叉树:构造二叉树登场! (opens new window),35.搜索插入位置 (opens new window)和59.螺旋矩阵II (opens new window)**都详细讲过循环不变量。
确定递归终止条件
这里定义的是左闭右闭的区间,所以当区间 left > right的时候,就是空节点
# Base Case if left > right: return None确定单层递归的逻辑
首先取数组中间元素的位置,不难写出
int mid = (left + right) / 2;,**这么写其实有一个问题,就是数值越界,例如left和right都是最大int,这么操作就越界了,在二分法 (opens new window)中尤其需要注意!**所以可以这么写:int mid = left + ((right - left) / 2);但本题leetcode的测试数据并不会越界,所以怎么写都可以。但需要有这个意识!取了中间位置,就开始以中间位置的元素构造节点,代码:
TreeNode* root = new TreeNode(nums[mid]);。接着划分区间,root的左孩子接住下一层左区间的构造节点,右孩子接住下一层右区间构造的节点。最后返回root节点,单层递归整体代码如下:
# 确定左右界的中心,防越界 mid = left + (right - left) // 2 # 构建根节点 mid_root = TreeNode(nums[mid]) # 构建以左右界的中心为分割点的左右子树 mid_root.left = self.traversal(nums, left, mid-1) mid_root.right = self.traversal(nums, mid+1, right) # 返回由被传入的左右界定义的某子树的根节点 return mid_root这里
int mid = left + ((right - left) / 2);的写法相当于是如果数组长度为偶数,中间位置有两个元素,取靠左边的。
递归整体代码如下
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# 递归解法
# time:O(N);space:O(height)= O(logN)
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
# 返回根节点
return self.traversal(nums,0,len(nums)-1)
# 定义区间不变量,左闭右闭[left,right]
def traversal(self,nums,left,right):
# base case
if left > right: return None
# 递归处理
# 确定左右界的中心,防越界
middle = left + (right-left)//2
# 构建根节点
newNode = TreeNode(nums[middle])
# 构建以左右界的中心为分割点的左右子树
newNode.left = self.traversal(nums,left,middle-1)
newNode.right = self.traversal(nums,middle+1,right)
# 返回由被传入的左右界定义的某子树的根节点
return newNode
3. 复杂度分析
时间复杂度:O(n)
其中 n 是数组的长度。每个数字只访问一次;
空间复杂度:O(logn)
其中 n 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是 O(logn)。
4. 思考与收获
(二刷再看)本题也有迭代写法;
迭代法可以通过三个队列来模拟,一个队列放遍历的节点,一个队列放左区间下标,一个队列放右区间下标。模拟的就是不断分割的过程,C++代码如下:(我已经详细注释)迭代的方法,其实就是模拟取中间元素,然后不断分割去构造二叉树的过程;
class Solution { public: TreeNode* sortedArrayToBST(vector<int>& nums) { if (nums.size() == 0) return nullptr; TreeNode* root = new TreeNode(0); // 初始根节点 queue<TreeNode*> nodeQue; // 放遍历的节点 queue<int> leftQue; // 保存左区间下标 queue<int> rightQue; // 保存右区间下标 nodeQue.push(root); // 根节点入队列 leftQue.push(0); // 0为左区间下标初始位置 rightQue.push(nums.size() - 1); // nums.size() - 1为右区间下标初始位置 while (!nodeQue.empty()) { TreeNode* curNode = nodeQue.front(); nodeQue.pop(); int left = leftQue.front(); leftQue.pop(); int right = rightQue.front(); rightQue.pop(); int mid = left + ((right - left) / 2); curNode->val = nums[mid]; // 将mid对应的元素给中间节点 if (left <= mid - 1) { // 处理左区间 curNode->left = new TreeNode(0); nodeQue.push(curNode->left); leftQue.push(left); rightQue.push(mid - 1); } if (right >= mid + 1) { // 处理右区间 curNode->right = new TreeNode(0); nodeQue.push(curNode->right); leftQue.push(mid + 1); rightQue.push(right); } } return root; } };构造二叉树的类型题:在二叉树:构造二叉树登场! (opens new window)和 二叉树:构造一棵最大的二叉树 (opens new window)之后,我们顺理成章的应该构造一下二叉搜索树了,一不小心还是一棵平衡二叉搜索树。其实思路也是一样的,不断中间分割,然后递归处理左区间,右区间,也可以说是分治;
利用递归函数返回值构造:此时相信大家应该对通过递归函数的返回值来增删二叉树很熟悉了,这也是常规操作;
区间循环不变量:在定义区间的过程中我们又一次强调了循环不变量的重要性;
取中间元素防止越界的办法:取数组中间元素的位置,不难写出
int mid = (left + right) / 2;,这么写其实有一个问题,就是数值越界,例如left和right都是最大int,这么操作就越界了,在二分法 (opens new window)中尤其需要注意!所以可以这么写:int mid = left + ((right - left) / 2);
Reference:
本题学习时间:60分钟。
LeetCode538. 把二叉搜索树转换为累加树
链接: 538. 把二叉搜索树转换为累加树 - 力扣(LeetCode)
1. 思路
一看到累加树,相信很多小伙伴都会疑惑:如何累加?第一反应是,遇到一个节点,然后在遍历其他节点累加?怎么一想这么麻烦呢。 之前有说过,看到二叉搜素树要意识到它的中序遍历就是一个有序数组,所有BST的题目,可以理解为在一个有序数组上操作。
其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。
为什么变成数组就是感觉简单了呢?因为数组大家都知道怎么遍历啊,从后向前,挨个累加就完事了,这换成了二叉搜索树,看起来就别扭了一些是不是。那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,记录前一个节点的数值,然后顺序累加就可以了。
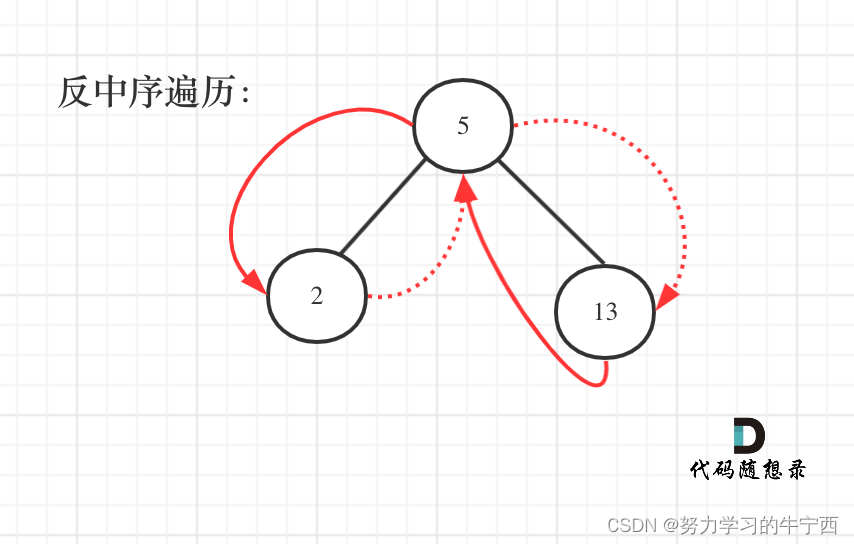
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
pre指针的使用技巧,我们在**二叉树:搜索树的最小绝对差 (opens new window)和二叉树:我的众数是多少? (opens new window)**都提到了,这是常用的操作手段。
2. 代码实现
递归三部曲
递归函数参数以及返回值
这里很明确了,不需要递归函数的返回值做什么操作了,要遍历整棵树。同时需要定义一个全局变量pre,用来保存cur节点的前一个节点的数值,定义为int型就可以了;
class Solution(object): def convertBST(self, root): """ :type root: TreeNode :rtype: TreeNode """ # pre指针记录前一个node的数值 global pre pre = None def traversal(self,node): # 因为要遍历整棵树,所以递归函数不需要返回值 global pre确定终止条件:遇空就终止;
# 终止条件 if node == None: return None确定单层递归的逻辑
注意要右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值;
# 反中序遍历,右中左 self.traversal(node.right) # 中间的处理就是,把当前node数值累加前一个pre数值 if pre != None: node.val += pre.val pre = node self.traversal(node.left)
递归法整体代码如下
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# time:O(N);space:O(height)=O(N)
class Solution(object):
def convertBST(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
# pre指针记录前一个node的数值
global pre
pre = None
self.traversal(root)
return root
def traversal(self,node):
# 因为要遍历整棵树,所以递归函数不需要返回值
global pre
# 终止条件
if node == None: return None
# 反中序遍历,右中左
self.traversal(node.right)
# 中间的处理就是,把当前node数值累加前一个pre数值
if pre != None:
node.val += pre.val
pre = node
self.traversal(node.left)
3. 复杂度分析
时间复杂度:O(n)
其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n)
为递归过程中栈的开销,平均情况下为 OO(logn),最坏情况下树呈现链状,为 O(n);
4. 思考与收获
- 迭代写法是中序遍历模板题;
# 迭代解法
# 中序遍历模板题
# time:O(N);space:O(N)
class Solution(object):
def convertBST(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
pre = None
if root == None: return None
stack = []
cur = root
while cur or stack:
if cur:
stack.append(cur)
cur = cur.right
else:
cur = stack.pop()
if pre != None:
cur.val += pre.val
pre = cur
cur = cur.left
return root
- 本题也属于BST双指针的应用;
Reference:
本题学习时间:60分钟。
二叉树总结
reference: 代码随想录 (programmercarl.com)
本篇学习时间近4小时,总结字数近10000字;在修剪BST中更加深入地理解了递归的过程;有序数组转化为BST中,又一次用到了切割数组递归的思路;把BST转化为累加树中,再一次用到了双指针技巧。(求推荐!!)