无人机集群一直是当今研究的热点与难点。然而，目前相关的集群规划策略通常缺乏在杂乱环境中避开障碍的能力。为了解决无人机在密集复杂环境下的编队避障飞行这一难题，浙江大学 Fast Lab 实验室提出了一种分布式无人机集群轨迹优化算法——Swarm-Formation。依靠这套算法，让无人机能够实现在密集环境中规划出无碰撞的无人机编队轨迹，确保编队飞行过程中无碰撞轨迹生成。

该算法提出了一种新的可微度量来量化编队之间的总体相似距离，然后将该度量公式化为一个优化框架，该框架使用多项式轨迹实现时空规划，能够将碰撞惩罚最小化，从而同时处理编队保持和避障问题。Swarm-Formation 算法为无人机集群科研人员及工程师提供了无人机集群避障的新思路。

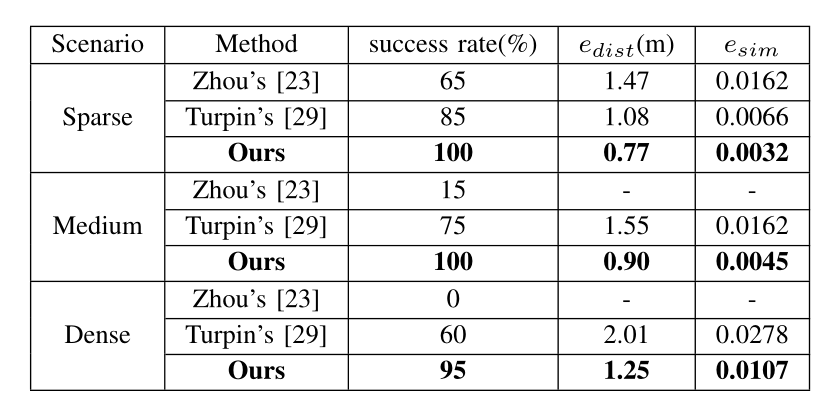
SwarmFormation算法对比

相比于其他方法，本算法的优化方法在位置误差和编队相似性误差上取得了良好的性能。因其提出的编队相似度量方法在缩放和旋转不变性为生成轨迹提供了很高的灵活性，即使在密集的环境中，也有很高的成功率去规划生成无碰撞编队轨迹。

SwarmFormation算法浅析

该算法来自浙江大学 Fast Lab 实验室的《Distributed Swarm Trajectory Optimization for Formation Flight in Dense Environments 》论文（论文及代码地址见文末），该论文中提出了一种密集环境下编队飞行的分布式集群轨迹优化方法，使用一种基于图的可微度量来量化无人机编队之间的距离。将无人机编队飞行的轨迹生成归结为一个优化问题，通过将代价函数最小化来得到一条保持编队飞行的无碰撞平滑轨迹。而代价函数由七个目标函数及其相对应的权重组成，分别为平滑度惩罚、总时间惩罚、碰撞项惩罚、集群编队惩罚、机间碰撞惩罚、动力学可行性惩罚和约束点的均匀分布惩罚。

平滑度惩罚

无人机轨迹使用高阶多项式表示，将轨迹的三阶导数加加速度(jerk)作为控制输入，最小化高阶导数能够使得整段轨迹控制能量小。所以将全局轨迹的jerk的平方作为惩罚性，可以让生成的无人机轨迹控制能量小，并且使得轨迹平滑。

总时间惩罚

对于无人机集群编队飞行而言，我们希望编队加权总执行的时间小一些，即编队能更快的达成规划目标。

碰撞项惩罚

欧式符号距离场(ESDF)可以计算出无人机和障碍物之间的距离信息和梯度信息，当无人机轨迹的约束点离最近障碍物的距离小于安全距离时，将生成的无人机轨迹推离障碍物。

集群编队惩罚

使用无向图对无人机编队进行建模，每个无人机为无向图的顶点，无向图的边表示无人机之间可以相互测量彼此之间的几何距离，并且每个无人机均能与其他无人机通信。定义一个编队相似距离度量，其为当前队形无向图的归一化拉普拉斯矩阵减去期望队形的归一化拉普拉斯矩阵，用于评估三维工作空间中无人机队形与期望队形的差异。通过惩罚编队相似距离度量，即可以让无人机集群尽可能去接近期望队形。需要注意的是，无人机队形的平移、旋转不会影响无人机之间的拓扑，且由于将无向图的拉普拉斯矩阵归一化，故无人机队形的平移、选择、放缩不会影响编队相似距离度量。

机间碰撞惩罚

在本算法中，由于采用的是非合作框架，即意味着无人机会接收其他无人机的轨迹作为约束来生成自己的轨迹。并且通过在全局时间戳处让约束点远离其他的无人机轨迹，实现无人机的轨迹之间不会相互碰撞。

动力学可行性惩罚

限制无人机轨迹导数即无人机的速度、加速度、加加速度的振幅，确保算法生成的轨迹可以让无人机平缓的执行。

约束点的均匀分布

生成的无人机轨迹包含了多个约束点，无人机约束点应该是空间均匀的。非均匀约束点可能会跳过一些较小的障碍物，这可能会降低轨迹的安全性。本算法通过惩罚每对相邻约束点之间距离平方的方差来实现约束点的均匀分布。

以上七个目标函数加上其权重就可以计算出某一条轨迹的代价成本，成本最小也就意味着这条轨迹是最优的轨迹，根据实际情况以及不同的应用场景相应的权重值也应做适当的调整。

我们近期也把这一套算法开源的ROS功能包与PX4仿真进行结合，在gazebo仿真平台上复现了该套算法并取得了不错的表现，下面就是我们PX4无人机应用Swarm Formation的仿真测试视频：

相关论文及代码

论文：https://arxiv.org/pdf/2109.07682.pdf 

代码地址：https://github.com/ZJU-FAST-Lab/Swarm-Formation

- END -