引言：

在之前我们系统的学习了数据结构中基础的概念、时间复杂度，并且用代码实现了顺序表（Contiguous_List），在对顺序表的学习和实现的文章总结中，我们提到了顺序表的优势在于可以直接访问顺序表中任意一个元素，但是劣势在于如果再头部或者中间位置进行插入或者删除操作，移动元素所产生时空开销较大。在这篇文章中我们将要进行学习的链表（Linked_List）在计算机内存中不一定连续，也可以有效的降低插入和删除元素所产生的时空开销，但相比较顺序表有着优秀时空开销的链表同样也有它的缺点，我们将对链表进行系统的学习并使用代码对他进行实现。

数据结构学习目录：

数据结构系列学习(一) - An Introduction to Data Structure

数据结构系列学习（二） - 顺序表详解（Contiguous_List） 

学习：

为了避免插入和删除所产生的巨大的时空开销，线性表有另外一种表现形式——链表。链表相较于顺序表不同的是链表并不是连续存储的。

链表是由一些列不必在内存中相连的结构组成的。每一个结构均含有表元素和指向包含该元素后继元素的结构的指针。我们也把这个指针叫做Next指针。最后一个单元的Next指针指向NULL，此处的NULL为0.

特点：逻辑相邻，但是物理上并不一定相邻
因为数据元素在物理上并不要求连续，则是虚了顺序表可以随机访问的优势
单链表：用一组任意的存储单元，存储线性表的数据元素（这组数据可以连续，也可以不连续。
所以为了表示每个节点An和其后继节点An+1之间逻辑关系，每一个节点不仅仅需要保存自己的有效值（数值域），还需要保存下一个节点的地址（指针域））
单链表一般分为两种实现方式：带头节点（常用）、不带头节点（实现起来相对比较麻烦）

代码实现：

注：这里我们实现的是不带头节点的单链表。

链表的结构体设计：

在学习链表的过程中，我们已经知道链表包含数据域（data）和指针域（next），我们在设计结构体的时候也应该与这两个东西保持一致，在这里我们先重新定义范型int类型为Elem_type，所以链表中的数据域自然也就是Elemtype类型了，链表中的指针域就是链表结构体类型的指针：

typedef int Elem_type;//给出范型重命名
typedef struct Node{
    Elem_type data;//数据域(保存数据的有效值)
    struct Node* next;//指针域（保存有效节点，也就是node的节点）
}Node,*PNode;//将结构体重命名为Node，结构体类型的指针变量命名为PNode

函数功能说明：

实现链表首先要明确的就是我们即将要实现的链表能做什么，也就是链表应该具有哪些功能，下面就是链表应该具有的功能：

初始化函数（Init_List）

头部插入函数(Insert_head)

尾部插入函数(Insert_tail)

按位置插入函数(Insert_pos)

头部删除函数(Delete_head)

尾部删除函数(Delete_tail)

按位置删除函数(Delete_pos)

按值删除函数(Delete_val)

查找函数(Search)

判空函数(IsEmpty)

清空函数(Clear)

销毁函数(Destroy)

打印函数(Show)

头文件（Linked_List.h）中的函数声明：

//1 初始化
void Init_List(struct Node* plist);
//2 头插
bool Insert_head(struct Node* plist,Elem_type val);
//3 尾插
bool Insert_tail(struct Node* plist,Elem_type val);
//4 按位置插
bool Insert_pos(struct Node* plist,int pos,Elem_type val);
//5 头删
bool Delete_head(struct Node* plist);
//6 尾删
bool Delete_tail(struct Node* plist);
//7 按位置删
bool Delete_pos(struct Node* plist,int pos);
//8 按值删
bool Delete_val(struct Node* plist,Elem_type val);
//9 查找 返回的是查找到的这个节点的地址
struct Node* Search(struct Node* plist,Elem_type val);
//10 判空
bool IsEmpty(struct Node* plist);
//10 清空
bool Clear(struct Node* plist);
//11 销毁
bool destroy(struct Node* plist);
//11 打印
void Show(struct Node* plist);

源文件（Linked_List.cpp） 中函数功能的具体实现：

初始化函数（Init_List）:

我们要初始化链表首先要做的就是将plist的指针域置为NULL：

代码：

void Init_List(struct Node* plist)
{
    //1 判断plist是否为空地址(安全性处理)
    assert(plist != NULL);
    //2 对于plist指向的头节点里面的每一个成员变量进行赋值
    plist->next = nullptr;//将链表中的头节点的next赋值为空
}

插入函数组（Insert）： 

在写插入函数组之前，我们首先应该知道对于链表中的插入操作（头部插入、尾部插入、按位置插入）到底是怎样完成的，这里我们给出一张图：

我们以上面画的链表结构图为例子，这是链表的初始状态、pnewnode代表的是待插入的新节点：

我们知道，在不带头节点的单链表中初始节点的数据域为空，且Next指针指向下一个节点的数据域，那么如果我要执行插入操作，我就操纵本来应该指向下一个节点数据域的Next指针这时指向pnewnode节点的数据域，然后再操纵pnewnode的next指针指向下一个节点的数据域，使其形成一个环形结构即可，如图：

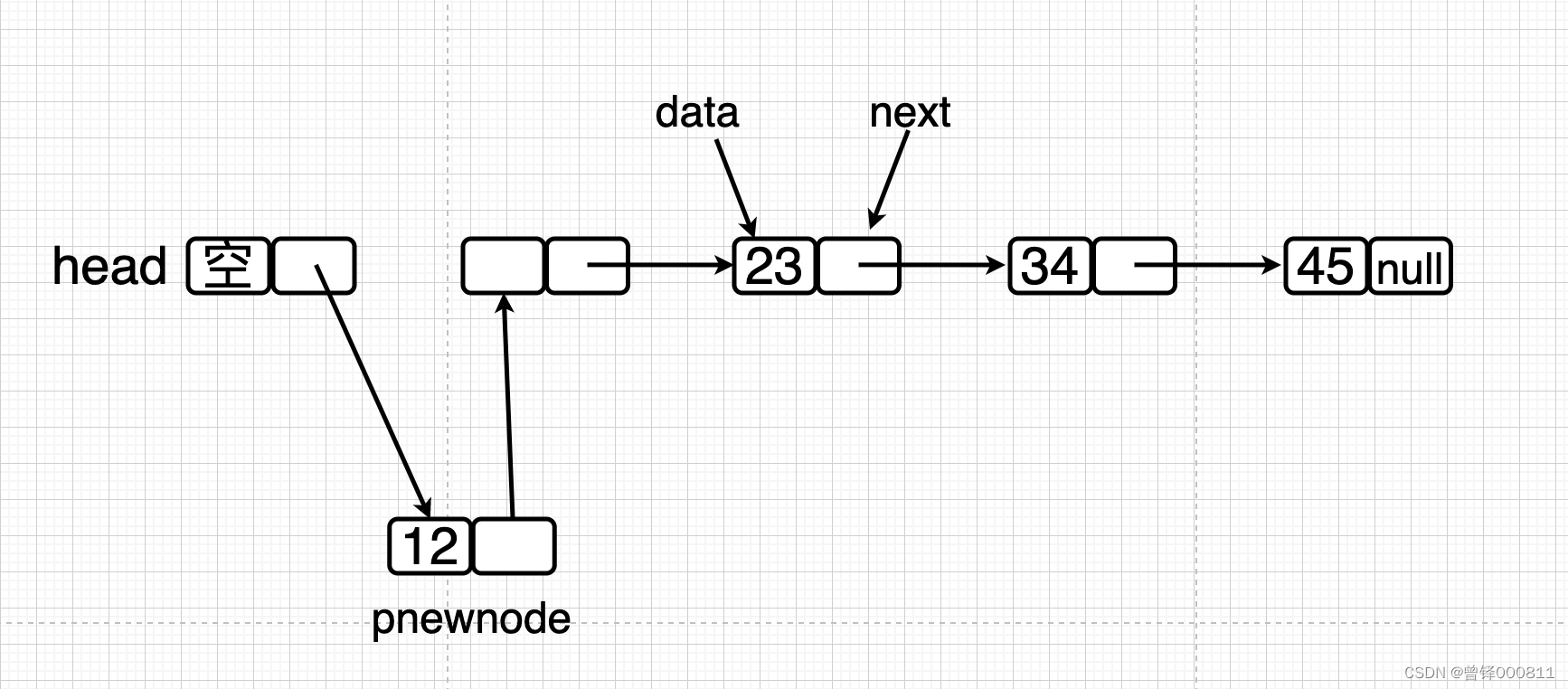
这就是链表中插入的操作演示。 

问题：链表的插入需不需要判满？

在写头部插入函数之前，我们先来探讨一个问题，链表的插入需不需要判满？

在之前的顺序表的文章中曾经说过，顺序表是我们申请的一整块连续的内存，顺序表在存储结构和物理上都是连续的，因此在顺序表的插入和删除操作中，我们首先要做的就是判断顺序表是否已满，如果满了就进行扩容操作再进行添加或删除操作，如果没满就直接进行添加或删除操作，顺序表的添加或删除操作是将被移动元素前面或者后面的全部元素进行移动，时空开销较大。

相较于顺序表，链表本身是是线性表的另一种表现形式，链表在存储结构上连续，但在物理上是不连续的。链表中存在两个成员一个是存储数据的数据域另一个是指阵域，存储下一个节点的地址，这也就是在链表中物理空间不连续但是在存储结构上是连续的原因。链表中的节点都是一步步通过malloc函数申请而得来的，申请完节点之后，通过对新节点的数据域进行赋值，通过修改指针域的指向来达到添加新节点的目的，所以只要堆区还有足够的空间，链表就无需判满。

头部插入函数(Insert_head)：

我们要插入数据，就必须要在链表新节点的数据域中存放该数据，而链表的新节点是需要通过malloc函数在堆区进行申请的，所以大致的过程就能表示为：对指针做安全性处理，在堆区申请pnewnode新节点的内存空间，申请完成之后将数据存放在新节点的数据域中，修改pnewnode的next域，然后再更新plist的头节点：

代码：  

bool Insert_head(struct Node* plist,Elem_type val)
{
    //1 安全性处理
    assert(plist != NULL);
    //2 购买新节点
    struct Node* pnewnode = (struct Node*)malloc(1 * sizeof(struct Node));
    // 安全性处理
    assert(pnewnode != NULL);
    //3 插入数据
    pnewnode->data = val;
    //4 插入操作 将新节点的next指向前驱节点的next
    pnewnode->next = plist->next;
    //将新节点的地址赋值给前驱节点的next域（这里的前驱节点就是原先的头节点plist）
    plist->next = pnewnode;
    return true;
}

尾部插入函数(Insert_tail)：

和写头部插入函数相似，我们在写尾部插入函数的时候，也需要先申请新节点，将我们要插入的值赋值给新节点的数据域，修改原先末尾节点的next，使其保存新节点的地址，然后将新节点的next赋值为空：

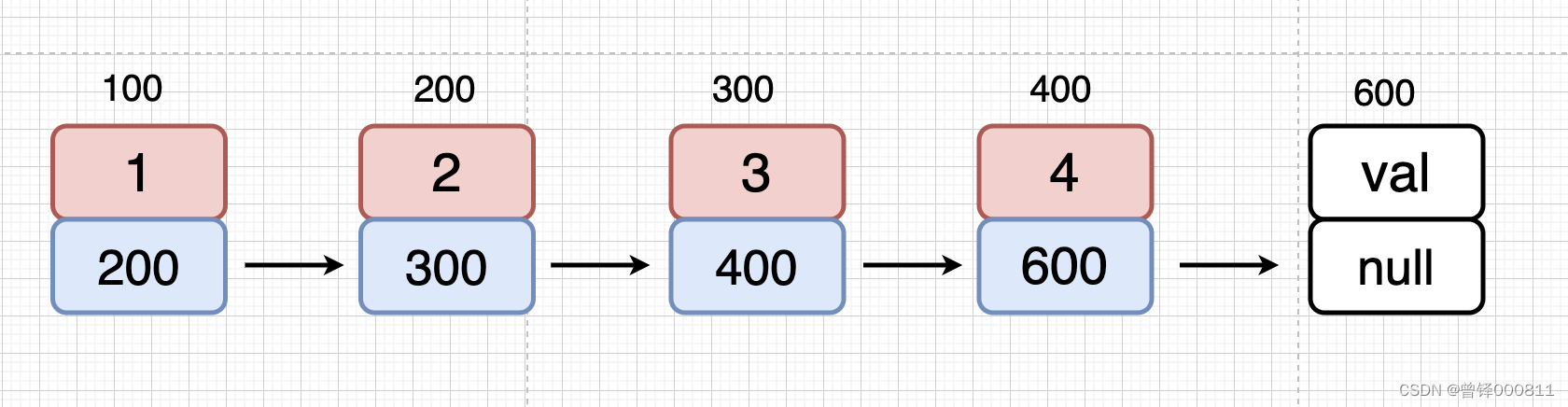
代码：

bool Insert_tail(struct Node* plist,Elem_type val)
{
    //1 安全性处理
    assert(plist != nullptr);
    //2 购买新节点
    struct Node* pnewnode = (struct Node*)malloc(1 * sizeof(struct Node));
    assert(pnewnode != nullptr);
    pnewnode->data = val;
    //3 使用一个新指针指向链表的头部
    pnewnode->next = nullptr;
    //4 申请新指针
    struct Node *p = plist;
    //5 通过for循环找到需要插入的位置
    //注：不需要前驱的函数，例如查找、判断有效值的个数，打印函数直接使用指向头节点的for循环即可
    //但是这里我们是需要前驱的，所以使用指向头节点的for循环进行遍历
    for(;p->next!= nullptr;p=p->next){
        p->next = pnewnode;
    }
    pnewnode->next = p->next;
    p->next = pnewnode;
    return true;
}

按位置插入函数(Insert_pos)：

我们默认pos = 0为头插，pos等于0时

代码：

bool Insert_pos(struct Node* plist,int pos,Elem_type val)
{
    //1 安全性处理
    assert(plist != nullptr && pos >= 0 && pos <= Get_length(plist));
    //2 购买新节点
    struct Node* pnewnode = (struct Node *)malloc(1 * sizeof(struct Node));
    //3 找到待插入位置
    struct Node *p = plist;
    for(int i = 0;i < pos;i++){
        p = p->next;
    }
    pnewnode->next = p->next;
    p->next = pnewnode;
    return true;
}

删除函数组（Delete）： 

头部删除函数(Delete_head)：

代码：

bool Delete_head(struct Node* plist)
{
    //1 安全性处理
    assert(plist != NULL);
    //2 判空
    if(IsEmpty(plist)){
        return false;
    }
    //3 申请一个新指针p指向待删除节点
    struct Node *p = plist->next;
    //4 申请一个新指针q指向待删除节点前面的节点（前驱）
//    struct Node *q = plist; 因为头删的上一个节点就是头节点
    //5跨越指向（让待删除节点上一个节点的next域保存下一个节点的地址）
    plist->next = p->next;
    //释放待删除节点
    free(p);
    return true;
}

尾部删除函数(Delete_tail)：

代码：

bool Delete_tail(struct Node* plist)
{
    //1 安全性处理
    assert(plist != NULL);
    //2 判空
    if(IsEmpty(plist)){
        return false;
    }
    struct Node *p = plist;
    for(;p->next != nullptr;p = p->next);//此时for循环执行结束，p指向尾节点
    struct Node *q = plist;
//    for(;q->next->next = nullptr;q = q->next);
    for(;q->next != p;q = q->next);
    p->next = q->next;
    free(p);
    return true;
}

按位置删除函数(Delete_pos)：

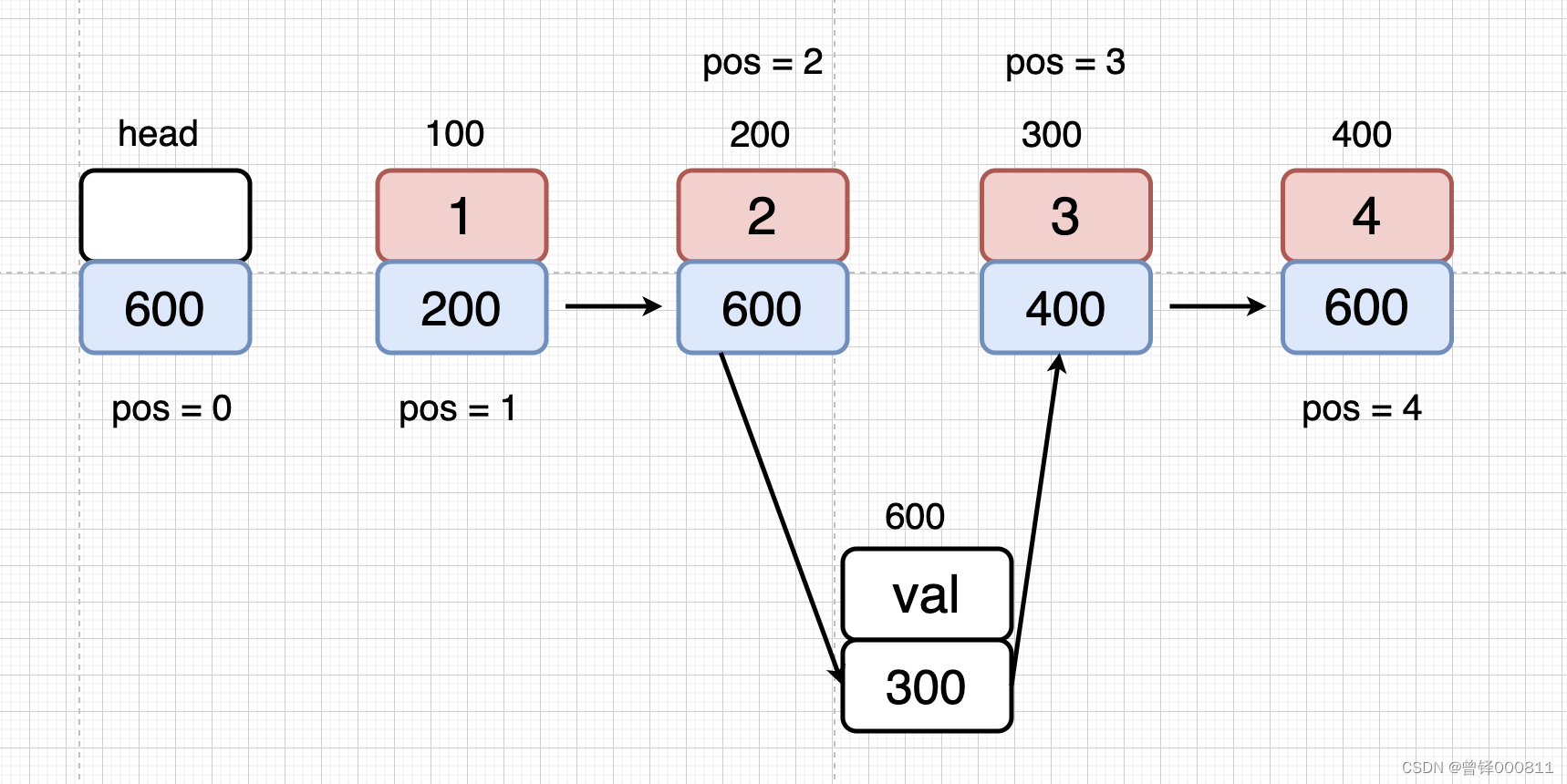
代码：

bool Delete_pos(struct Node* plist,int pos)
{
    //1 安全性处理
    assert(plist != NULL && pos >= 0 && pos != Get_length(plist));
    if(IsEmpty(plist)){
        return false;
    }
    struct Node *q = plist;
    for(int i = 0;i < pos;i++){
        q = q->next;
    }
    struct Node *p = plist;
    p = q->next;
    q->next = p->next;
    free(q);
    return true;
}

按值删除函数(Delete_val)：

代码：

bool Delete_val(struct Node* plist,Elem_type val)
{
    //1 安全性处理
    assert(plist != nullptr);
    if(IsEmpty(plist)){
        return false;
    }
    struct Node *p = Search(plist,val);
    if(p == nullptr){
        return false;
    }
    struct Node *q = plist;
    for(; q->next != p;q = q->next);
    q->next = p->next;
    free(p);
    return true;
}

查找函数(Search)：

我们在之前写插入和删除函数的时候，如果是按位置插入删除或者按值进行删除的话需要通过循环来找到目标位置，而且在插入或者删除函数中的操作通常都是需要使用到节点的前驱的，所以在定义新指针的时候我们通常使用新指针保存的是头节点的地址。但是在查找函数中，我们并不需要使用节点的前驱，我们只需要读取节点的数据域即可，所以我们就使用新定义的指针保存第一个有效节点即可。

用代码来表示需要前驱的for循环：

struct Node *p = plist;//plist为头节点的地址
for(struct Node *p;p->next != nullptr;p = p->next)

用代码来表示不需要前驱的for循环：

struct Node *p = plist -> next;
for(struct Node *p;p != nullptr;p = p->next)

查找函数代码：

struct Node* Search(struct Node* plist,Elem_type val)
{
    //1 安全性处理
    assert(plist != NULL);
    if(IsEmpty(plist)){
        return NULL;
    }
    for(struct Node *p = plist ->next;p != nullptr;p = p->next){
        if(p->data == val){
            return p;
        }
    }
    return nullptr;
}

判空函数(IsEmpty)：

bool IsEmpty(struct Node* plist)
{
    //2 当头节点的next指针指向空，则代表单链表为空
    return plist->next == nullptr;
}

清空函数(Clear)：

销毁函数(Destroy)：

打印函数(Show)：

代码：

void Show(struct Node* plist)
{
    //1 安全性处理
    assert(plist != NULL);
    //2 定义新指针指向链表
    struct Node *p = plist->next;
    for(;p!= nullptr;p = p->next){
        printf("%3d", p->data);
    }
}

获取长度函数(Get_length)：

int Get_length(struct Node* plist)
{
    assert(plist != nullptr);
    int count = 0;
    struct Node *p = plist->next;
    for(;p!= nullptr;p = p->next){
        count++;
    }
    return count;
}

参考资料：

严蔚敏 - 《数据结构（C语言版）》 - 清华大学出版社

Mark·Allen·Weiss - 《数据结构与算法分析（C语言描述）》 - 机械工业出版社