树
(一)、树型结构
1.树的定义:
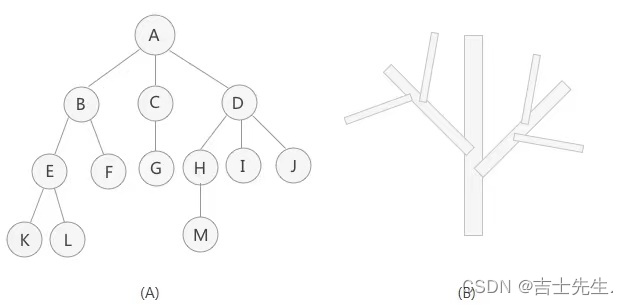
树是一种数据结构,它是由n(n≥0)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个结点有零个或多个子结点(n>=0);没有父结点的结点称为根节点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树。(一对多的关系,。没有节点这一说)
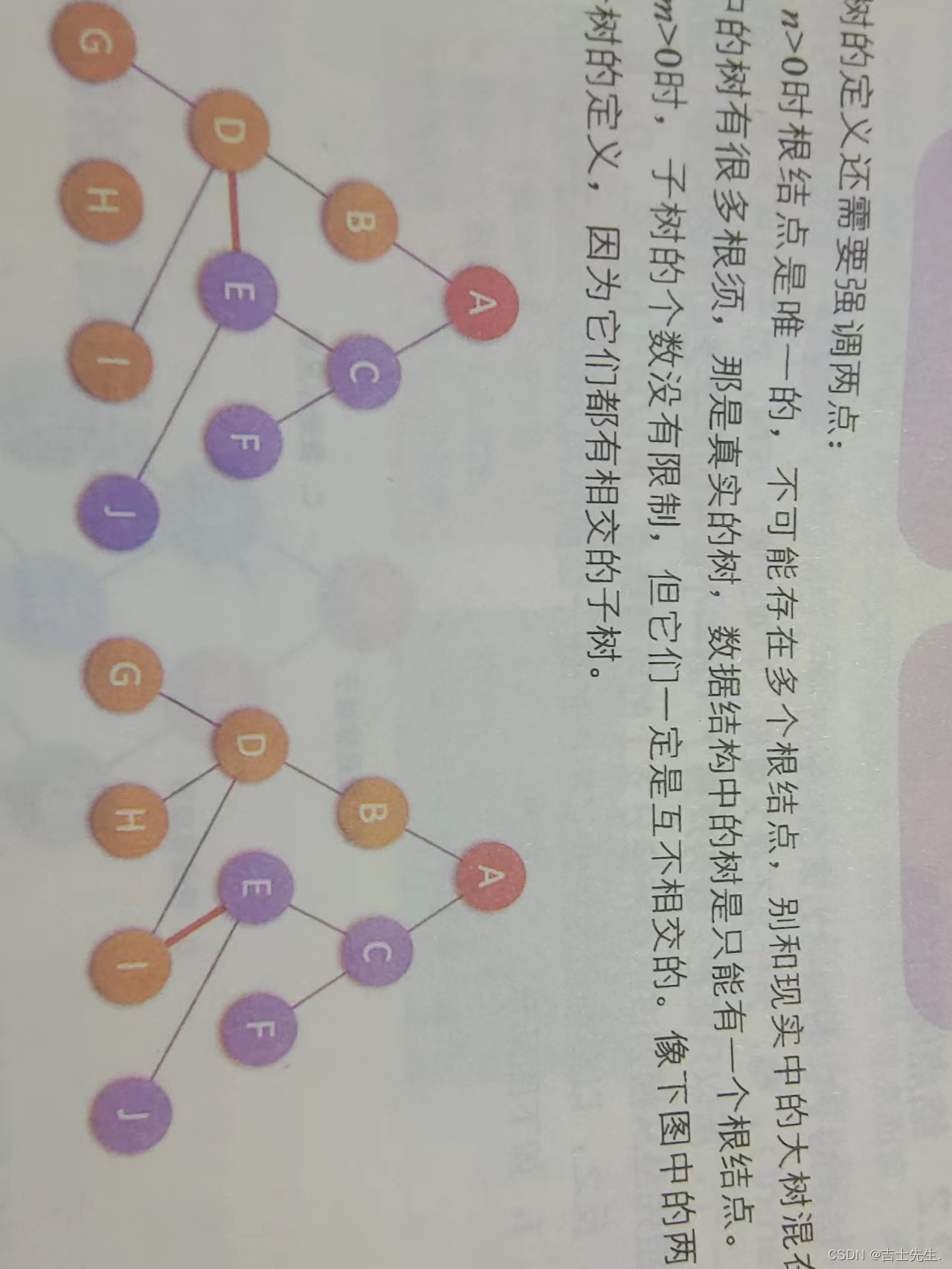
2.树需要注意的地方
1.一个树只能有一个根结点,但可以有多个子结点。
2.子结点的个数没有限制,但是子结点一定不能相交互。
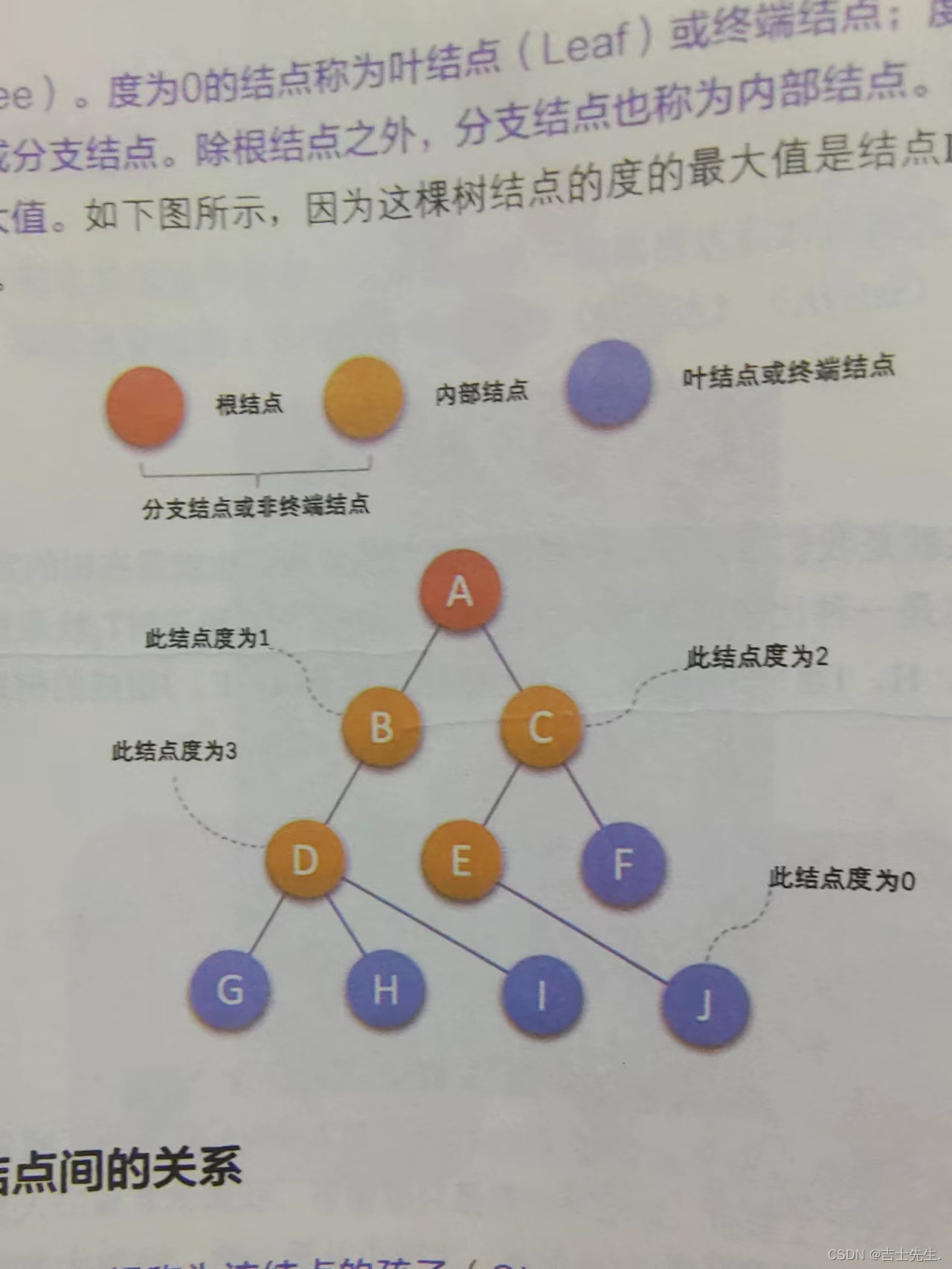
3.结点的分类:(树的度 节点的度)
树的结点包含一个数据元素及若干个指向其子树的分支。结点拥有的子树数称为结点的度(Degree)。度为0的结点称为叶结点(Leaf)或终端结点;度不为0的结点称为非终端结点或分支支结点。除根结点之外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。
4.结点间的关系:
结点的子树的根称为该结点的孩子(Child),相应的,该结点称为孩子的双亲(Parent)(注意是双亲,不是单亲)。同一个双亲的孩子之间互称兄弟(Sibling)。结点的祖先是从根到该结点所经分支上的所有结点。以某结点为根的子树中的任一结点都称为该结点的子孙。
5.树的其他相关概念:
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度。
如果将树中结点的各子树看成从左至右是有次序的,不能互换,则称该树为有序树,否则为无序树。
森林(Forest)是m(m>=0)棵互不相交的树的集合。
根结点没有父结点,其他的结点都有一个父结点,
子结点 :父结点的下一层。
叶子结点:没有子结点的结点。
结点的度:结点的子结点数。
树的度:最多的叶结点的度。
结点的层:根结点为1,依次类推。
高度 :树的最大层。
森林:
(二)、二叉树
二叉树的定义:
二叉树的每个结点的子结点最多只有两个子树的树结构。也就是说树的度为2
满二叉树的定义:
每一层的结点树都达到最大值。
完全二叉树的定义:
设二叉树的深度为k,除第k层外,其他各层(1~(k-1))的结点数都达到最大值。第k层所有的结点都连续集中在最左边,这就是完全二叉树。
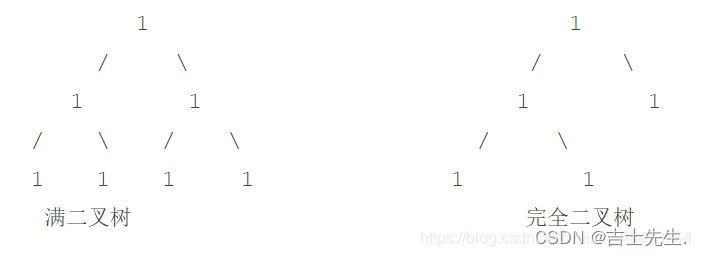
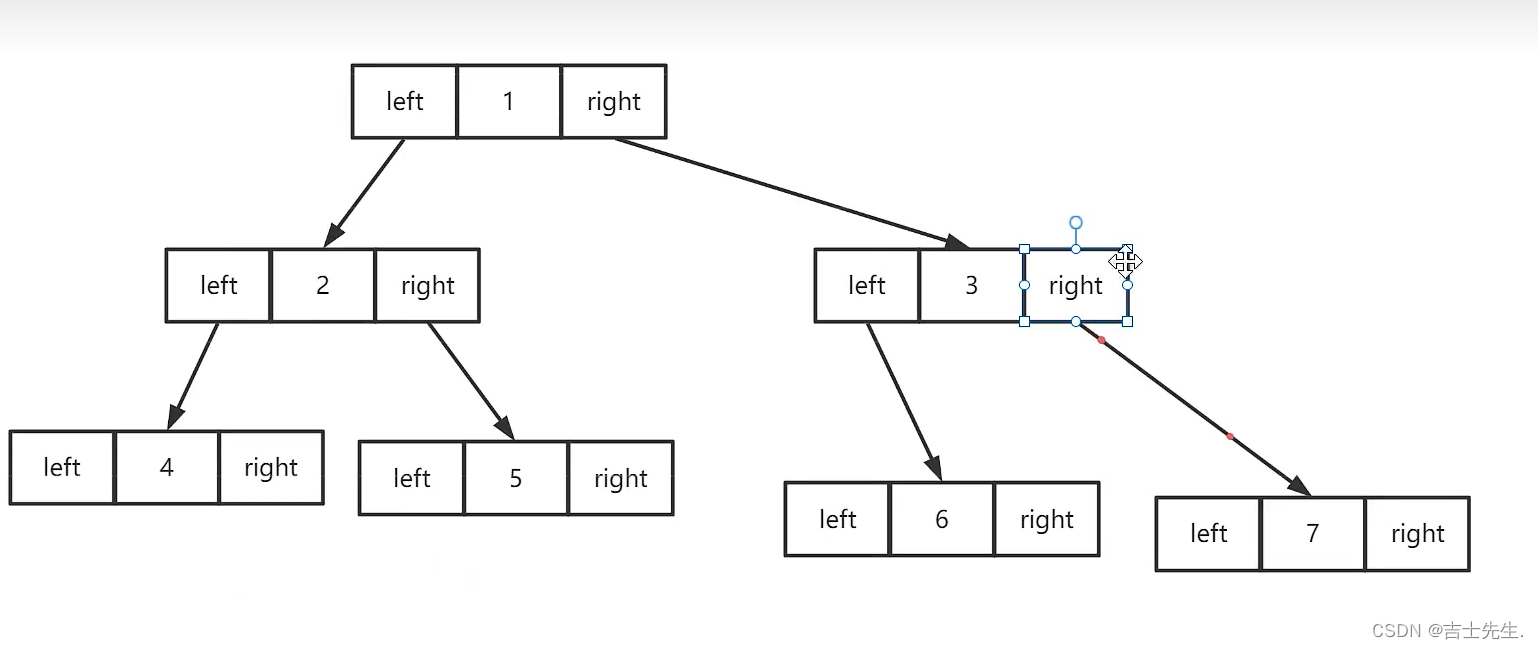
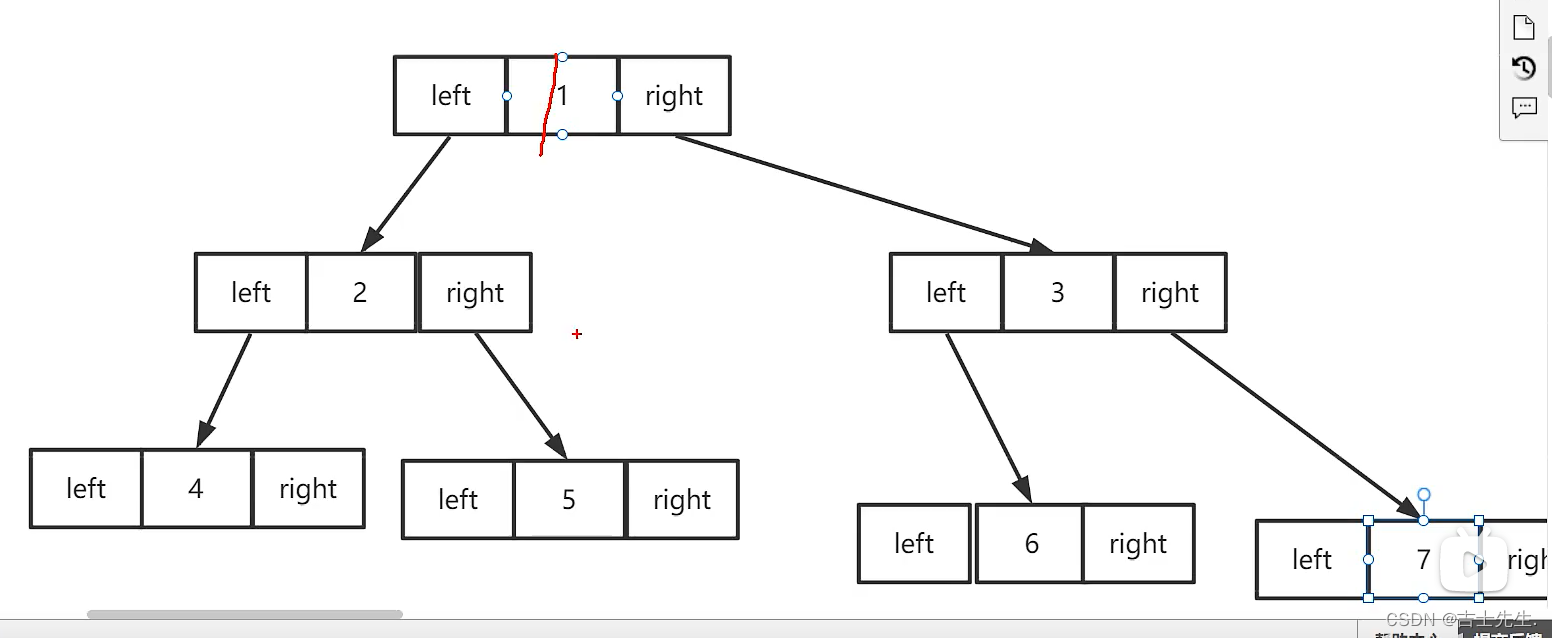
1.二叉树的创建:
创建结点:
public class Node{
//数值
Object item;
//左右子结点
Node left;
Node right;
public Node(Object item){
this.item=item;
}
}
创建树:
public void CreateTree() {
//创建根节点
root=new Node(1);
//第二层
//创建左子结点
Node Left=new Node(2);
//创建右子结点
Node Right=new Node(3);
//进行关联
root.left=Left;
root.right=Right;
//第三层
Node Left2=new Node(4);
//创建右子结点
Node Right2=new Node(5);
//进行关联
root.left.left=Left2;
root.left.right=Right2;
//第三层
Node Left3=new Node(6);
//创建右子结点
Node Right3=new Node(7);
//进行关联
root.right.left=Left3;
root.right.right=Right3;
}
前序遍历:
public void ShowTree(Node node){
if(node==null){
return;
}
//遍历根节点
System.out.println(node.item);
//遍历左子树
ShowTree(node.left);
//遍历右子树
ShowTree(node.right);
}
中序遍历:
public void MidShowTree(Node node){
if(node==null){
return;
}
//遍历左子树
MidShowTree(node.left);
//遍历根节点
System.out.println(node.item);
//遍历右子树
MidShowTree(node.right);
}
后序遍历:
public void FinShowTree(Node node){
if(node==null){
return;
}
//遍历左子树
FinShowTree(node.left);
//遍历右子树
FinShowTree(node.right);
//遍历根节点
System.out.println(node.item);
}
层次:
public void LeveTree(Node node){
//创建队列;
ArrayDeque <Node> ad=new ArrayDeque<>(10);
//加入根节点
ad.add(node);
while (!ad.isEmpty()) {
Node n=ad.poll();
System.out.println(n.item);
//左子树放到队列
if(n.left!=null){
ad.add(n.left);
}
//将右子树放到队列中去
if(n.right!=null){
ad.add(n.right);
}
}
}
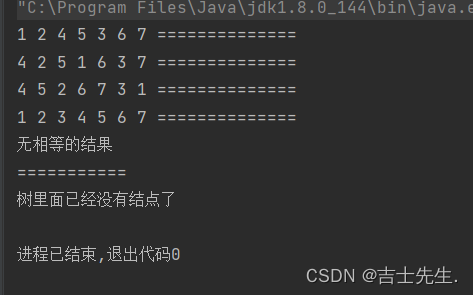
全部代码:
1.1.全部代码:
import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {
public static void main(String []avgs){
Tree t=new Tree();
t.CreateTree();
t.ShowTree(t.root);
System.out.println("==============");
t.MidShowTree(t.root);
System.out.println("==============");
t.FinShowTree(t.root);
System.out.println("==============");
t.LeveTree(t.root);
System.out.println("==============");
Tree.Node result=t.Select(t.root,13);
if(result==null){
System.out.println("无相等的结果");
}else{
System.out.println("有相等的结果为:"+result.item);
}
System.out.println("===========");
t.Delete(t.root,1);
t.LeveTree(t.root);
}
}
import java.util.ArrayDeque;
public class Tree{
//定义一个根节点
Node root;
//创建结点
public static class Node{
//数值
Object item;
//左右子结点
Node left;
Node right;
//判断当前左右指针是否线索化
boolean isLeftLine=false;
boolean isRightLine=false;
public Node(Object item){
this.item=item;
}
}
//创建一棵树
public void CreateTree() {
//创建根节点
root=new Node(1);
//第二层
//创建左子结点
Node Left=new Node(2);
//创建右子结点
Node Right=new Node(3);
//进行关联
root.left=Left;
root.right=Right;
//第三层
Node Left2=new Node(4);
//创建右子结点
Node Right2=new Node(5);
//进行关联
root.left.left=Left2;
root.left.right=Right2;
//第三层
Node Left3=new Node(6);
//创建右子结点
Node Right3=new Node(7);
//进行关联
root.right.left=Left3;
root.right.right=Right3;
}
//前序遍历
public void ShowTree(Node node){
if(node==null){
return;
}
//遍历根节点
System.out.print(node.item+" ");
//遍历左子树
ShowTree(node.left);
//遍历右子树
ShowTree(node.right);
}
//中序
public void MidShowTree(Node node){
if(node==null){
return;
}
//遍历左子树
MidShowTree(node.left);
//遍历根节点
System.out.print(node.item+" ");
//遍历右子树
MidShowTree(node.right);
}
//后序遍历
public void FinShowTree(Node node){
if(node==null){
return;
}
//遍历左子树
FinShowTree(node.left);
//遍历右子树
FinShowTree(node.right);
//遍历根节点
System.out.print(node.item+" ");
}
//层次遍历:
public void LeveTree(Node node){
//创建队列;
ArrayDeque <Node> ad=new ArrayDeque<>(10);
if(node==null){
System.out.println("树里面已经没有结点了");
return;
}
//加入根节点
ad.add(node);
while (!ad.isEmpty()) {
Node n=ad.poll();
System.out.print(n.item+" ");
//左子树放到队列
if(n.left!=null){
ad.add(n.left);
}
//将右子树放到队列中去
if(n.right!=null){
ad.add(n.right);
}
}
}
//查找元素:
public Node Select(Node node,Object t){
Node target=null;
if(node==null){
return null;
}else{
if(node.item==t){
return node;
}else{
//从左子树进行遍历
target=Select(node.left,t);
//判断是否找到了结果
if(target!=null){
return target;
}
//从右子树进行遍历
target=Select(node.right,t);
//判断是否找到了结果
if(target!=null){
return target;
}
return null;
}
}
}
//删除元素:
public void Delete(Node node,Object t){
if(node==null){
return;
}
//判断根节点
if(node==root&&root.item==t){
this.root=null;
}
//判断子结点是否为null
if(node.left!=null){
if(node.left.item==t){
//删除左子结点
node.left=null;
return;
}else{
Delete(node.left,t);
}
}
//判断右子结点
if(node.right!=null){
if(node.right.item==t){
//删除右子结点
node.right=null;
return;
}else{
Delete(node.right,t);
}
}
}
//二叉树的深度
public int MaxDelth(Node node){
if(node==null){
return 0;
}
int leftDeth=0;
int rightDeth=0;
//获取左子树的高度
if(node.left!=null){
leftDeth=MaxDelth(node.left);
}
//获取右子树的高度
if(node.right!=null){
rightDeth=MaxDelth(node.right);
}
//判断最大层次关系
if(leftDeth>rightDeth){
return leftDeth+1;
}
else{
return rightDeth+1;
}
}
}
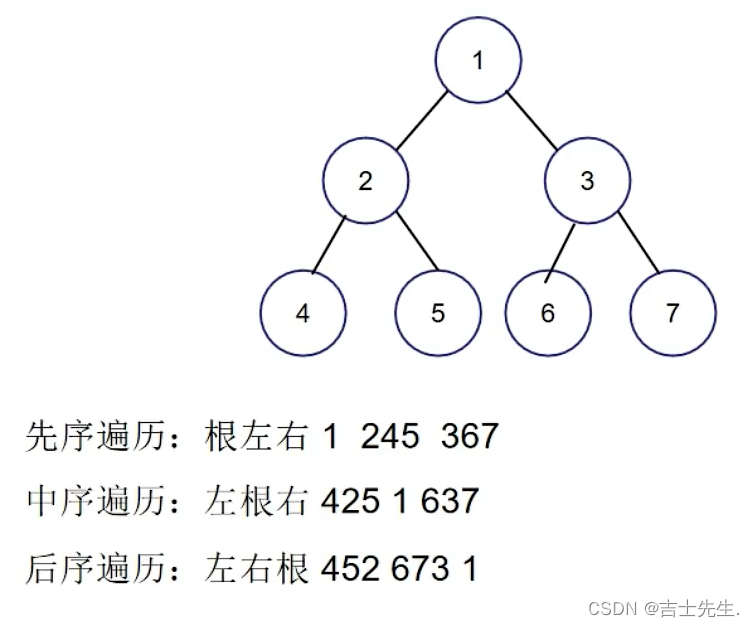
2.二叉树的遍历规则:
前序遍历: 根结点-左子树-右子树;
中序遍历:左子树-根结点-右子树;
后序遍历:左子树-右子树-根节点;
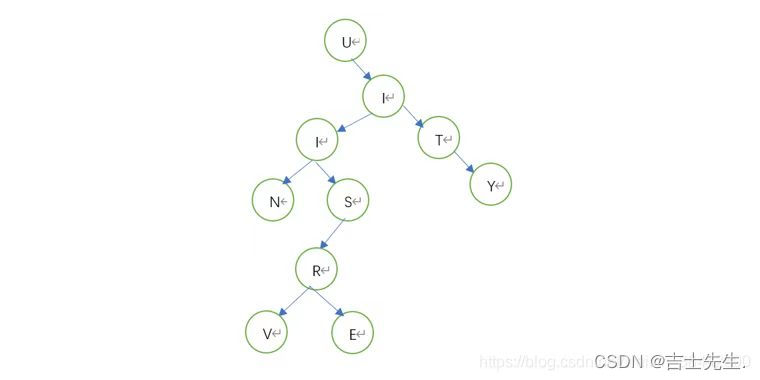
前序遍历:
前序遍历的遍历顺序是根左右。
我们首先从根节点U出发,由于它是根节点因此U排在首位,得到顺序U。
然后去找U的左节点,发现U没有左节点,于是去找U的右分支,得到顺序UI。
发现I有左节点I,得到顺序UII。
发现I有左节点N,得到顺序UIIN。
发现I有右节点S,得到顺序UIINS。
发现S有左节点R,得到顺序UIINSR。
发现R有左节点V,得到顺序UIINSRV。
发现R有右节点E,得到顺序UIINSRVE。
发现I有右节点T,得到顺序UIINSRVET。
发现I有右节点Y,得到顺序UIINSRVETY。
前序遍历从根节点出发,然后去找他的左节点,再找右节点,深度优先。
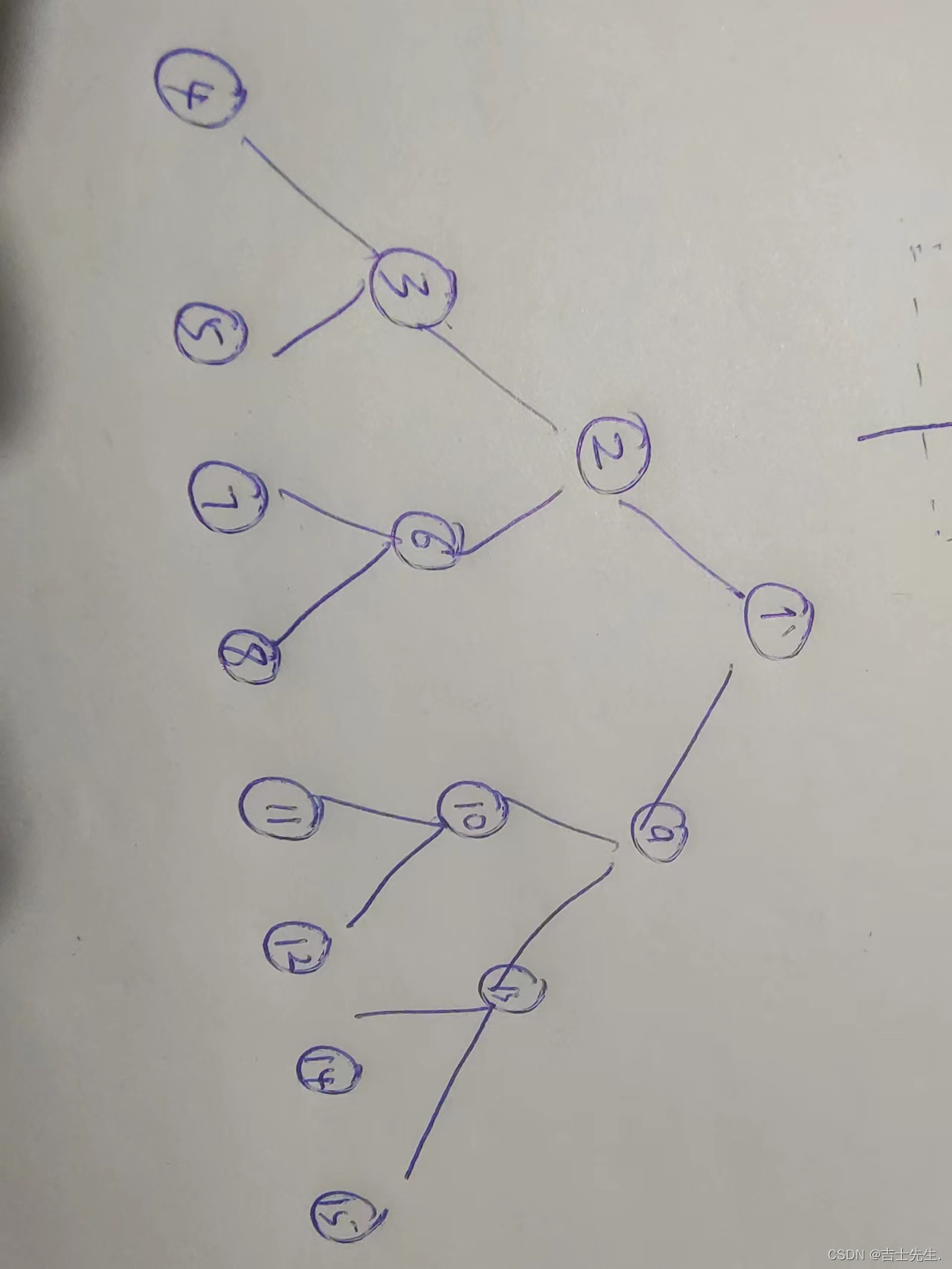
(三)、数组实现二叉树
n是下标不是数字哈
1.必须是完全二叉树.
2.左子节点是2n+1;
3.右子节点是2n+2;
4.父类子结点是(n-1)/2;
5.n代表从第几个(n初始化为0);
1.数组二叉树数组的遍历
public class array {
int []elem;
public array(int []s){
this.elem=s;
}
//实现先序遍历
public void preT(int idex){
if(idex>=elem.length){
return;
}
//遍历当前结点
System.out.print(elem[idex]+" ");
//遍历左节点
preT(2*idex+1);
//遍历右节点
preT(2*idex+2);
}
//遍历中序
public void midT(int idex){
if(idex>=elem.length){
return;
}
//遍历左节点
midT(2*idex+1);
//遍历当前结点
System.out.print(elem[idex]+" ");
//遍历右节点
midT(2*idex+2);
}
//遍历后序
public void laterT(int idex){
if(idex>=elem.length){
return;
}
//遍历左节点
laterT(2*idex+1);
//遍历右节点
laterT(2*idex+2);
//遍历当前结点
System.out.print(elem[idex]+" ");
}
}
import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {
public static void main(String []avgs){
array s1=new array(new int[]{1,2,3,4,5,6,7});
s1.preT(0);
System.out.println("===========");
s1.midT(0);
System.out.println("===========");
s1.laterT(0);
}
}
2.大堆顶的实现及其排序
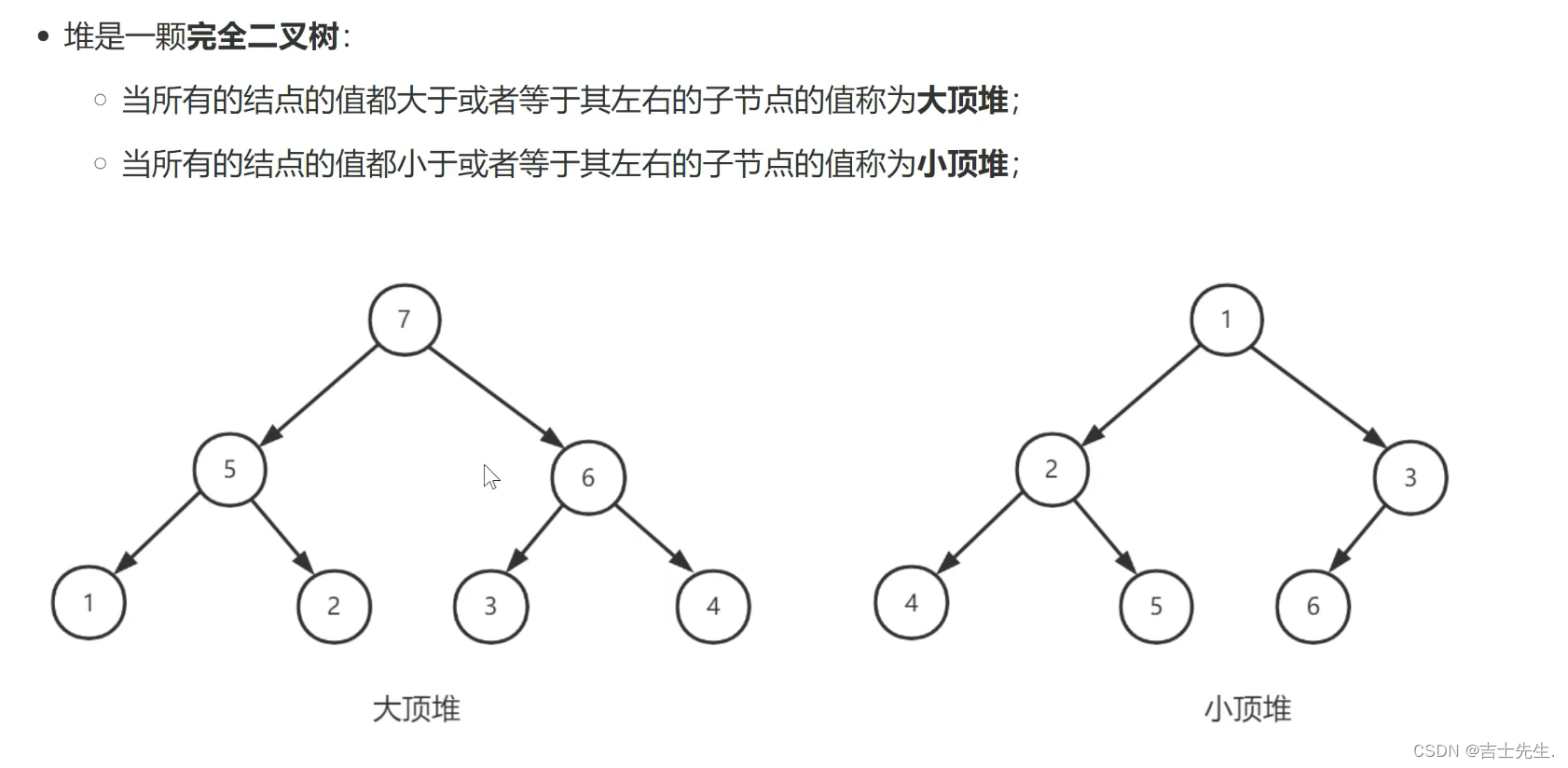
import org.jetbrains.annotations.NotNull;
import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {
public static void main(String []avgs){
int []arr=new int[]{9,19,3,2,18,7,8,25,29,4,20};
//构造二叉树的guize
//左结点 2*n+1;
//右节点 2*n+2;
//最后一个非叶子结点 :(arr.length-1)/2
//展现大顶堆
for (int i = (arr.length-1)/2; i >=0; i--) {
Dui(arr,i);
}
for (int i = 0; i <arr.length; i++) {
System.out.print(arr[i]+" ");
}
//实现大顶堆的排序 错错错
// for (int i = (arr.length-1)/2; i >=0; i--) {
// PaiDui(arr,i,arr.length);
// }
// //从数组的最后元素开始排序遍历
//
// for (int last=arr.length-1; last >=0 ; last--) {
// int temp=arr[0];
// arr[0]=arr[last];
// arr[last]=temp;
// //调用大堆顶排序的方法
// PaiDui(arr,0,last);
// }
// for (int i = 0; i <arr.length; i++) {
// System.out.print(arr[i]+" ");
// }
}
//构造大顶堆
public static void Dui(int @NotNull []arr, int idex){
//计算左子树的位置
int left=2*idex+1;
//计算右子树的位置
int right=2*idex+2;
//假如说子结点超过数组的位置,那么就退出
if(left>arr.length||right>arr.length){
return;
}
//比较大小
int max=idex;
if(arr[left]>arr[max]){
max=left;
}
if(arr[right]>arr[max]){
max=right;
}
if(max!=idex){
int temp;
temp=arr[idex];
arr[idex]=arr[max];
arr[max]=temp;
//还要向下进行比较
Dui(arr,max);
}
}
//构造大顶堆且进行排序
public static void PaiDui(int []arr,int idex,int size){
//计算左子树的位置
int left=2*idex+1;
//计算右子树的位置
int right=2*idex+2;
//假如说子结点超过数组的位置,那么就退出
if(left>size||right>size){
return;
}
//比较大小
int max=idex;
if(arr[left]>arr[max]){
max=left;
}
if(arr[right]>arr[max]){
max=right;
}
if(max!=idex){
int temp;
temp=arr[idex];
arr[idex]=arr[max];
arr[max]=temp;
//还要向下进行比较
PaiDui(arr,max,size);
}
}
}
(四).二叉查询树
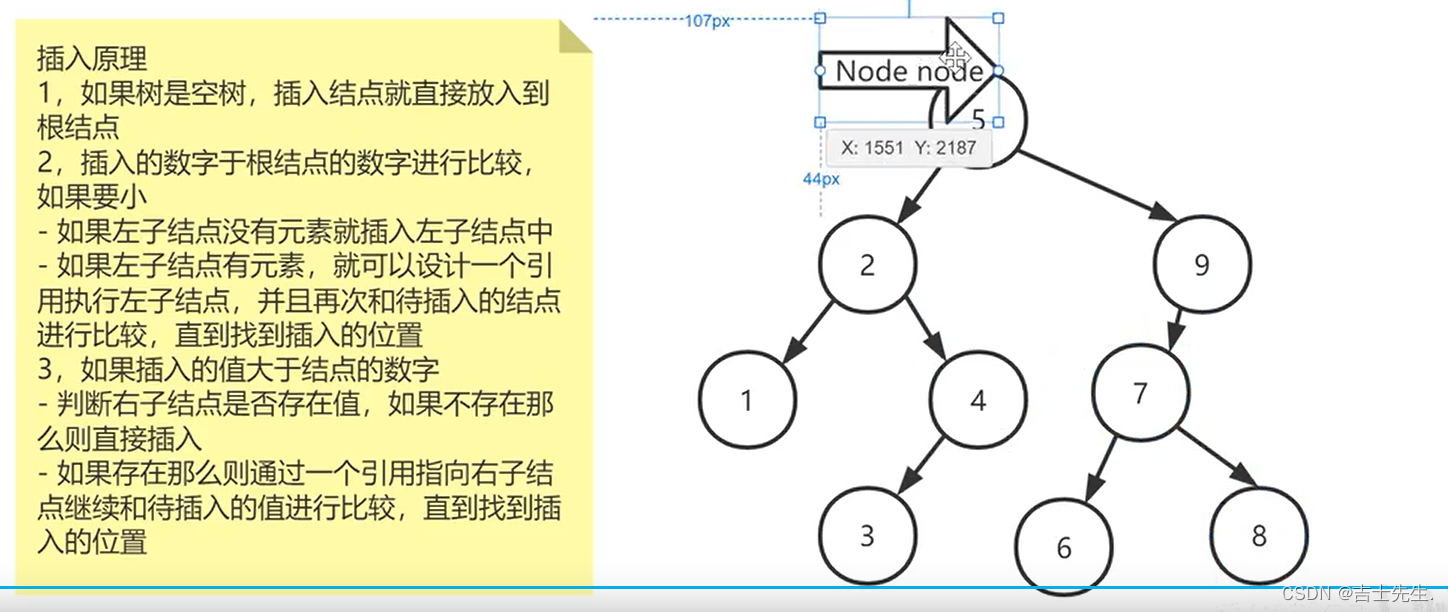
1.二叉查找树的插入原理
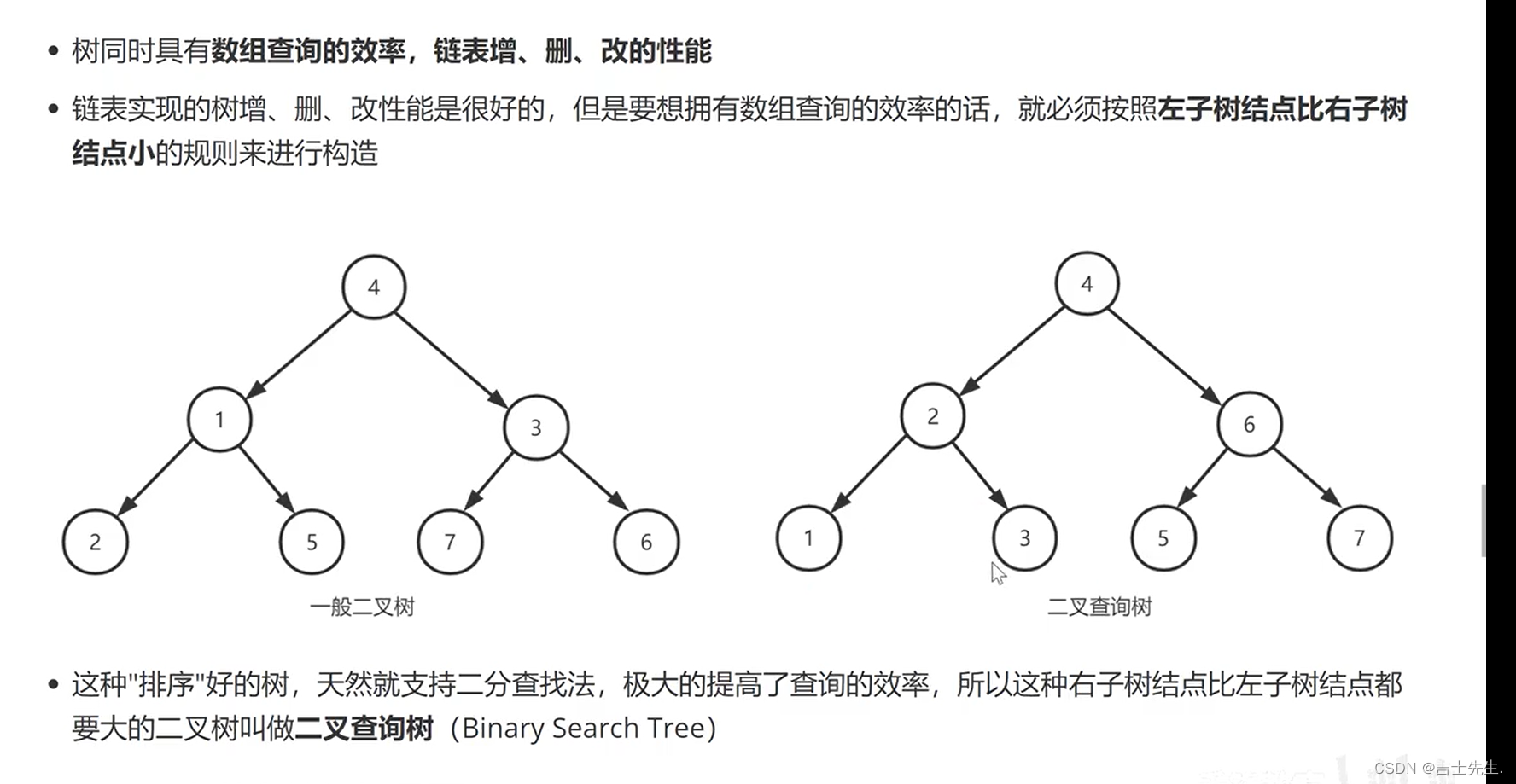
二叉树的插入原理:
假如说是空树。
1.那么插入的结点直接放到根节点的位置
假如说插入的数比父节点要小。
1.如果左字节点没有元素,那么就插入左子树。 2.如果左子结点有元素。那么就设计一个引用执行左结点,并且再次和待插入的结点进行比较,直到找到插入的位置。
如果插入的数比父节点要大。
1.如果右边不存在元素,那么就插入右子树。
2.如果右结点有元素那么 就引用一个执行右结点,并且再次和待插入的结点进行比较,直到找到插入的位置。
2.二叉查询树的顺序遍历:
使用树的中序遍历,即可达到二叉查询树的顺序遍历
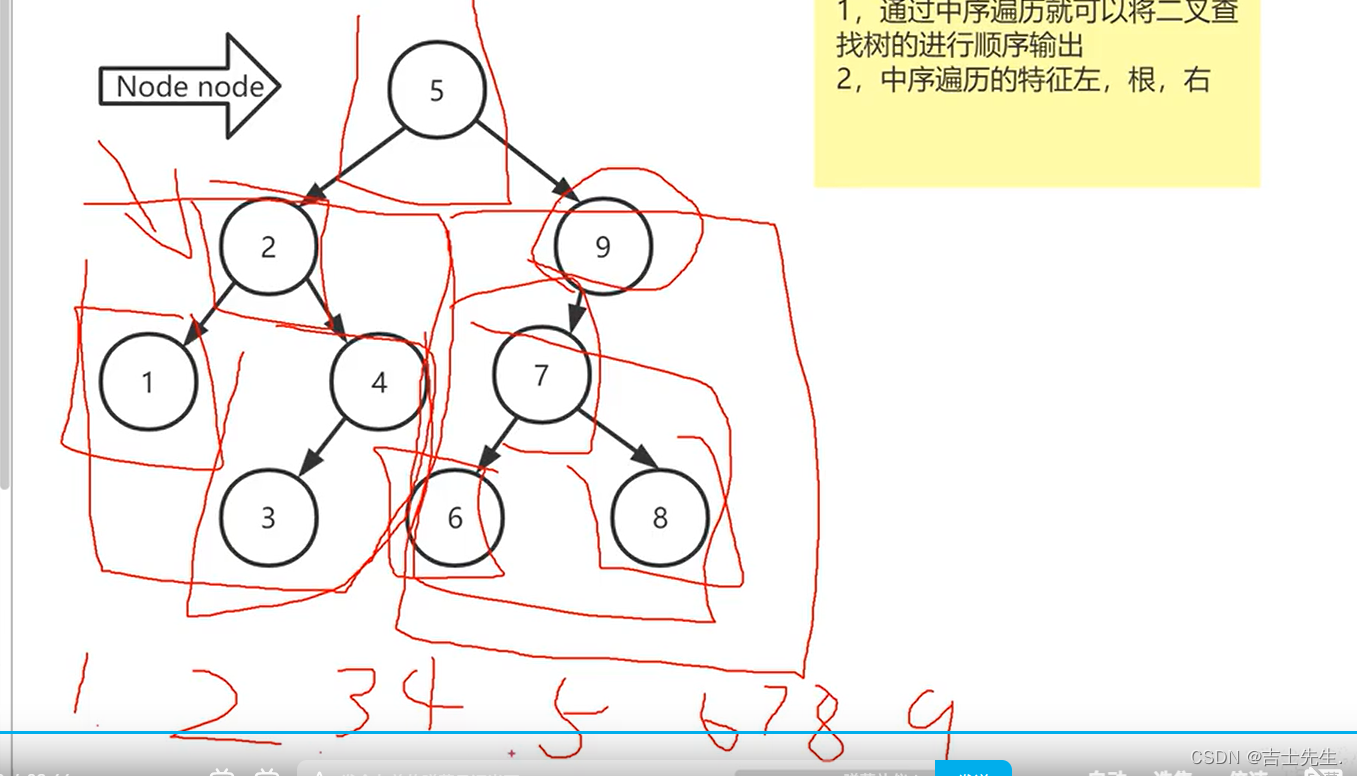
3.二叉查询树的查找原理
1.提供一个你要查找的值。
2.假如说查找的值比结点大,那么就走右子树,假如说比结点小,那么就走左子树。
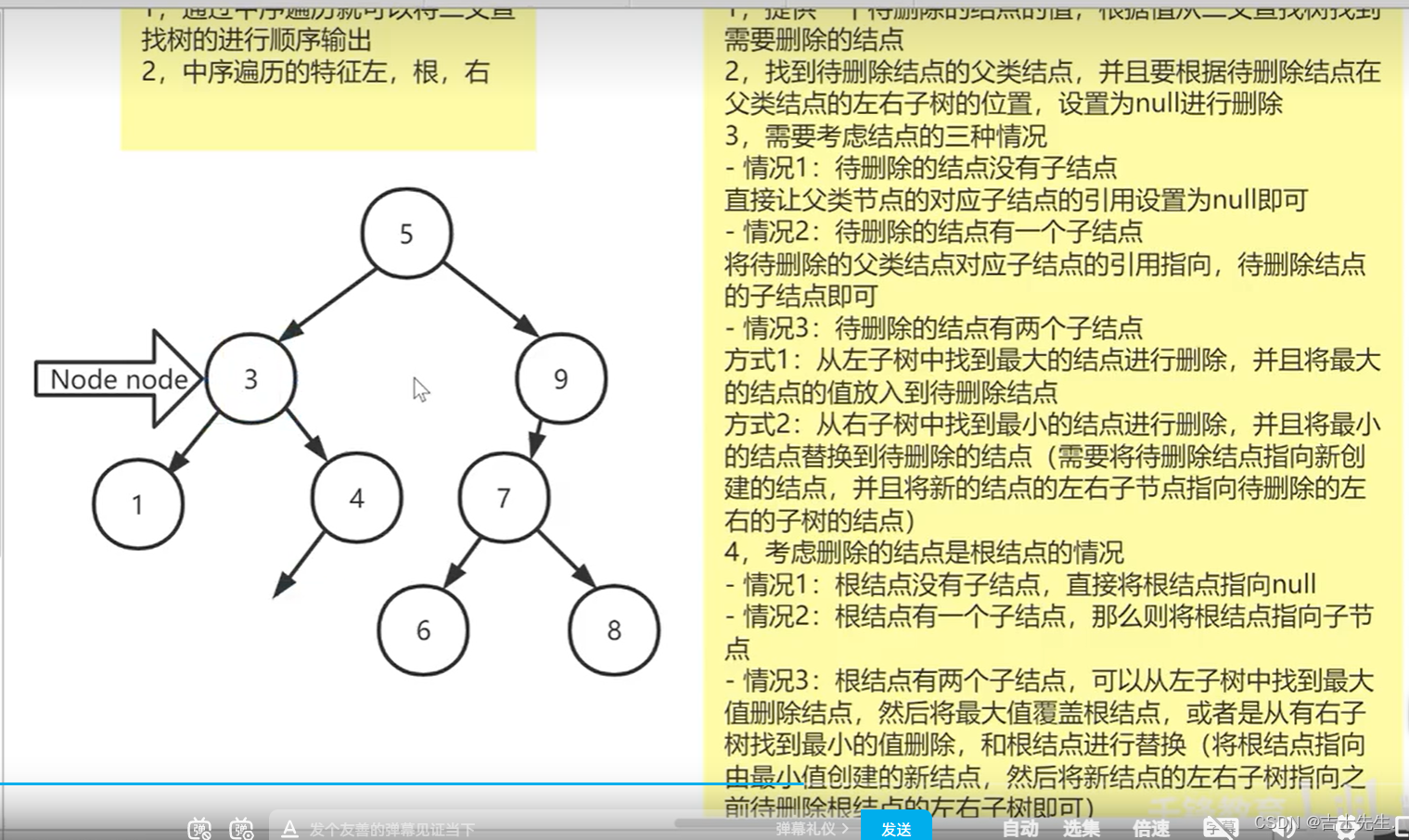
4.二叉查询树的删除原理
1.提供一个待删除结点的值,根据值从二叉树找到需要删除的值的结点。
2.找到待删除结点的父类结点,并且要根据待删除的点在父类的左右子树的位置,设置为null进行删除,
3.需要考虑结点的三种情况:
情况一:待删除的结点没有子结点
直接让父类结点的对应子结点的引用设置为null
情况二:待删除的结点有一个子结点
将待删除的父类结点对应的子结点的引用指向,待删除的结点的子结点即可。
情况三:待删除的结点有两个子结点
1.从左子树中找到最小的结点进行删除,并且将最大的结点的值覆盖到待删除结点。
2.从右子树找到最小的结点进行删除,并且将最小的结点替换到待删除的结点(需要将待删除的结点指向新创建的结点)
情况四:考虑删除的结点是根节点:
1.根结点没有子结点,直接将根节点指向null
2.根结点有一个子结点,直接将根节点指向子结点。
3.跟结点有两个子结点,可以从左子树中找到最大值删除结点,然后然后将最大值覆盖根节点。或则从右节点找到最小值和跟根节点进行替换(需要将跟结点指向新创建的结点,然后将新结点分别指向左右子树即可)
5.增删改查(全部代码)
import java.awt.*;
public class TreeSelect {
//创建树结点
public static class Node {
Node left;
Node right;
int value;
public Node(int value) {
this.value = value;
}
}
//设置根结点;
Node root;
//构造查询二叉树
public void insert(int value) {
//假如说根结点为空,那么直接把值给根节点
if (root == null) {
root = new Node(value);
} else {
//声明一个游标结点,开始指向根节点
Node idex = root;
while (true) {
//假如说插入的值小于游标的值
if (value < idex.value) {
//假如说游标左子结点没有值了,那么就把该值给游标的左边
if (idex.left == null) {
idex.left = new Node(value);
break;
} else {//假如说游标左子节点有值的话,那么就把游标指向游标的左子节点
idex = idex.left;
}
} else {
//如果游标右子节点没有值的话
if (idex.right == null) {
idex.right = new Node(value);
break;
} else {//如果不为空,那么就游标指向游标的右节点
idex = idex.right;
}
}
}
}
}
//实现中序遍历
public void MidTraversal(Node node) {
if (node == null) {
return;
}
//遍历左结点
MidTraversal(node.left);
//输出中结点
System.out.print(node.value + " ");
//输出右结点
MidTraversal(node.right);
}
//二叉树的删除
public static int LEFT = 0;
public static int RIGHT = 1;
public void deleteNdde(int value) {
//定义游标从根结点开始查询
Node idex = root;
//定义目标结点.
Node target = null;
//定义目标结点的父类结点
Node parent = null;
//定义目标结点的类型
int nodeType = 0; //0代表左子结点,1代表右子结点
//==========查值
while (idex != null) {
//假如说游标的值等于删除的值
if (idex.value == value) {
//找到了结点
target = idex;
break;
} else if (value < idex.value) {//假如说删除的值小于游标的值
//保存父节点
parent = idex;
//将游标节点指向左子节点
idex = idex.left;
nodeType = LEFT;
} else {
//保存父节点
parent = idex;
//将游标节点指向右子节点
idex = idex.right;
nodeType = RIGHT;
}
}
if(target==null){
System.out.println("没有找到要删除的结点");
}
//==========删除结点的三种情况
//情况一:没有子结点
if (target.left == null && target.right == null) {
if(parent==null){ //假如跟结点
//直接将rroot为空
root=null;
return;
}
//判断目标值的结点是左子节点还是右子节点
if (nodeType == LEFT) {
//将父类的左子节点设置为null
parent.left = null;
} else {
parent.right = null;
}
} else if (target.left != null && target.right != null) { //假如说有两个子结点
//从目标值的右子树方法中查找最小值的方法
Node min=target.right;
//遍历左子树
while (min.left!=null){
min=min.left;
}
//将最小的结点进行删除
deleteNdde(min.value);
//将待删除的结点与最小值进行替换
target.value=min.value;
} else {//假如只有一个子结点的情况
if(parent==null){ //加入删除根节点
if(target.left!=null){
root=target.left;
}else{
root=target.right;
}
return;
}
if (nodeType == LEFT) {
if (target.left != null) {
//将父类的子结点指向待删除结点的左子节点
parent.left = target.left;
} else {
//将父类的子节点指向待删除结点的右子结点
parent.left = target.right;
}
} else {
if (target.left != null) {
//将父类的子结点指向待删除结点的左子节点
parent.right = target.left;
} else {
//将父类的子节点指向待删除结点的右子结点
parent.right = target.right;
}
}
}
}
}
import org.jetbrains.annotations.NotNull;
import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {
public static void main(String []avgs){
int []arr=new int[]{5,2,1,4,3,9,7,6,8};
TreeSelect ts=new TreeSelect();
//将二叉树构造成查询二叉树
for(int i=0;i<arr.length;i++){
ts.insert(arr[i]);
}
ts.deleteNdde(11 );
//对查询二叉树进行遍历
ts.MidTraversal(ts.root);
}
}