LLC补偿网络
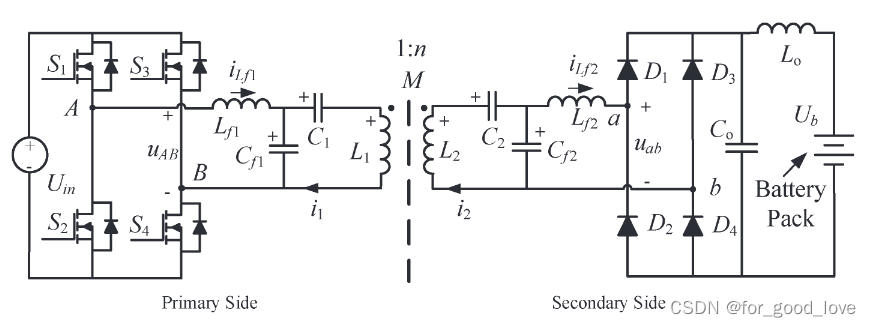
\qquad 其中Lf1/Lf2是原/副边补偿电感,Cf1/Cf2是原/副边并联补偿电容,C1/C2是原/副边串联补偿电容,L1/L2是原/副边电感。推导谐振条件如下,这是一个恒压谐振条件(CC/CV的谐振条件有很多,因此可以通过设置不同的工作频率来达到CC/CV输出)
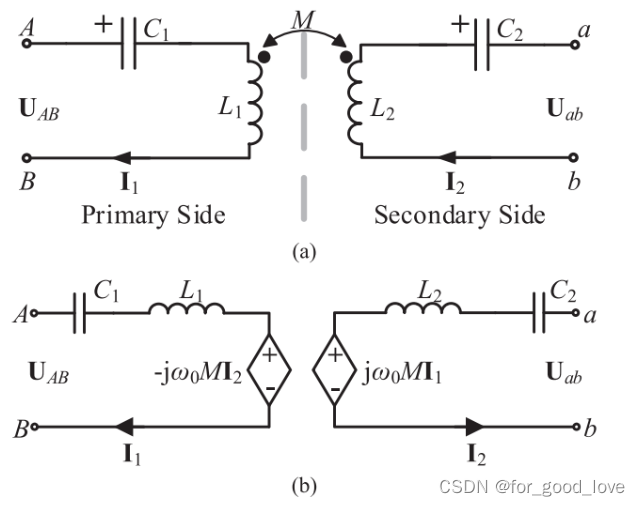
\qquad M模型如下:
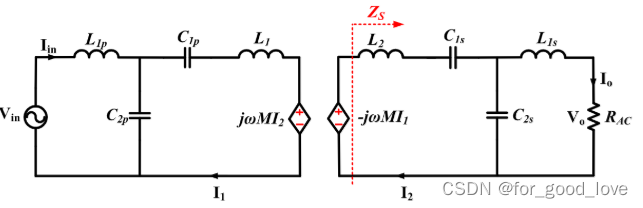 原边副边分别使用KVL有:
原边副边分别使用KVL有:
{ V i n = ( j w L 1 p − j 1 w C 2 p ) I i n − 1 j w C 2 p I 1 j w M I 1 = j ( w L 2 − 1 w C 1 s − 1 w C 2 s ) I 2 + j 1 w C 2 s I o \left\{ \begin{array}{lr} \bold {V_{in}}=\left(jwL_{1p}-j\cfrac{1}{wC_{2p}}\right)I_{in}-\cfrac{1}{jwC_{2p}}I_{1}\\ jwMI_{1}=j\left(wL_2-\cfrac{1}{wC_{1s}}-\cfrac{1}{wC_{2s}}\right)I_2+j\cfrac{1}{wC_{2s}}I_o \end{array} \right. ⎩
⎨
⎧Vin=(jwL1p−jwC2p1)Iin−jwC2p1I1jwMI1=j(wL2−wC1s1−wC2s1)I2+jwC2s1Io
\qquad 由上式得出,显然要是想Io与R无关。
I o = w 3 C 2 s C 2 p M V i n j = M V i n j w L 1 p L 1 s if : w L 1 p − 1 w C 2 p = 0 ( & & ) j ( w L 2 − 1 w C 1 s − 1 w C 2 s ) = 0 I_o=\cfrac{w^3C_{2s}C_{2p}MV_{in}}{j}=\cfrac{MV_{in}}{jwL_{1p}L_{1s}}\\ \text{if}:wL_{1p}-\cfrac{1}{wC_{2p}}=0(\&\&)j\left(wL_2-\cfrac{1}{wC_{1s}}-\cfrac{1}{wC_{2s}}\right)=0 Io=jw3C2sC2pMVin=jwL1pL1sMVinif:wL1p−wC2p1=0(&&)j(wL2−wC1s1−wC2s1)=0
\qquad 可以得到Zs的表达式
Z s = j ( w L 2 − 1 w C 1 s ) + ( − j 1 w C 2 s ) / / ( j w L 1 s + R A C ) = 1 w 2 R A C C 2 s 2 + j w C 2 s ( w 2 L 1 s C 2 s − 1 ) Z R = j w M I 2 I 1 = − w 2 M 2 Z s Z_s=j(wL_2-\cfrac{1}{wC_{1s}})+(-j\cfrac{1}{wC_{2s}})//(jwL_{1s}+R_{AC})=\cfrac{1}{w^2R_{AC}C_{2s}^2+jwC_{2s}(w^2L_{1s}C_{2s}-1)}\\ Z_R=\cfrac{jwMI_2}{I_1}=-\cfrac{w^2M^2}{Z_s} Zs=j(wL2−wC1s1)+(−jwC2s1)//(jwL1s+RAC)=w2RACC2s2+jwC2s(w2L1sC2s−1)1ZR=I1jwMI2=−Zsw2M2
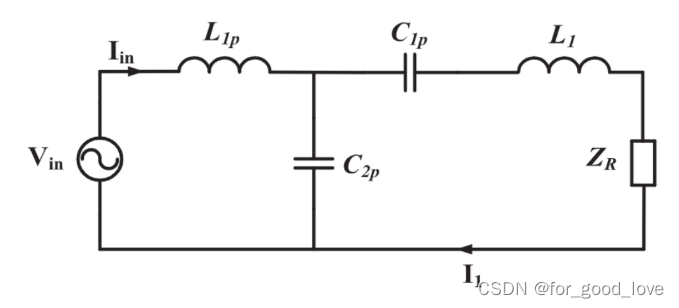
\qquad 从上图可以计算输入阻抗Zin Z i n = j w L 1 p + − j w 2 p / / ( − j w C 1 p + j w L 1 + Z R ) Z_{in}=jwL_{1p}+\cfrac{-j}{w_{2p}}//(\cfrac{-j}{wC_{1p}}+jwL_1+Z_R) Zin=jwL1p+w2p−j//(wC1p−j+jwL1+ZR)
\qquad 要想原边实现ZPA,那么Zin虚部为0,显然,如果利用上式求解较复杂,而且可能会出现多组解,那么可以采用电源等效的方式。
\qquad 由此可以得出CC谐振条件
L f 1 ⋅ C f 1 = 1 w 0 2 L f 2 ⋅ C f 2 = 1 w 0 2 ( L 1 − L f 1 ) ⋅ C 1 = 1 w 0 2 ( L 2 − L f 2 ) ⋅ C 1 = 1 w 0 2 L_{f1}\cdot C_{f1}=\cfrac{1}{w_0^2}\\ L_{f2}\cdot C_{f2}=\cfrac{1}{w_0^2}\\ (L_{1}-L_{f1})\cdot C_{1}=\cfrac{1}{w_0^2}\\ (L_{2}-L_{f2})\cdot C_{1}=\cfrac{1}{w_0^2}\\ Lf1⋅Cf1=w021Lf2⋅Cf2=w021(L1−Lf1)⋅C1=w021(L2−Lf2)⋅C1=w021
\qquad 下面按照论文A Double-Sided LCC Compensation Network and Its Tuning Method for Wireless Power Transfer中推导输出电流。
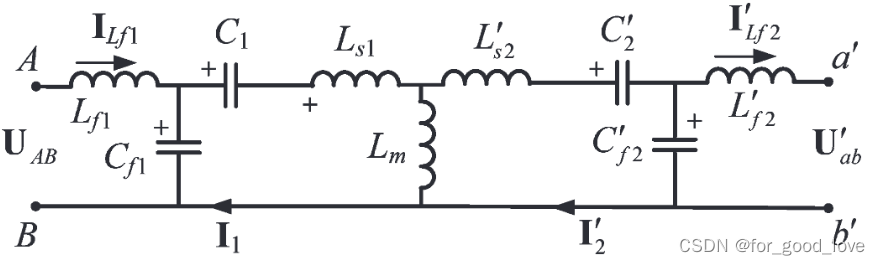
\qquad 去耦等效模型如上图
\qquad 折算关系 L m = k ⋅ L 1 L s 1 = ( 1 − k ) ⋅ L 1 L s 2 ′ = ( 1 − k ) ⋅ L 1 / n 2 L f 2 ′ = L f 2 n 2 C 2 ′ = n 2 ⋅ C 2 C f 2 ′ = n 2 ⋅ C f 2 U a b ′ = U a b n L_{m}=k\cdot L_1\\ L_{s1}=(1-k)\cdot L_1\\ L_{s2}'=(1-k)\cdot L_1/n^2\\ L_{f2}'=\cfrac{L_{f2}}{n^2}\\ C_{2}'=n^2\cdot C_2\\ C_{f2}'=n^2\cdot C_{f2}\\ U_{ab}'=\frac{U_{ab}}{n} Lm=k⋅L1Ls1=(1−k)⋅L1Ls2′=(1−k)⋅L1/n2Lf2′=n2Lf2C2′=n2⋅C2Cf2′=n2⋅Cf2Uab′=nUab
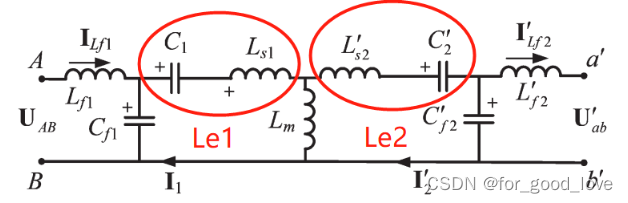
\qquad 其中
{ L e 1 = 1 j w 0 ( 1 j w 0 C 1 + j w 0 L s 1 ) = L f 1 − k L 1 L e 2 = 1 j w 0 ( 1 j w 0 C 2 ′ + j w 0 L s 2 ′ ) = L f 2 ′ − k L 1 \left\{ \begin{array}{lr} L_{e1}=\cfrac{1}{jw_0}\left(\cfrac{1}{jw_0C_1}+jw_0L_{s1}\right)=L_{f1}-kL_1\\ L_{e2}=\cfrac{1}{jw_0}\left(\cfrac{1}{jw_0C_2'}+jw_0L_{s2}'\right)=L_{f2}'-kL_1\\ \end{array} \right. ⎩
⎨
⎧Le1=jw01(jw0C11+jw0Ls1)=Lf1−kL1Le2=jw01(jw0C2′1+jw0Ls2′)=Lf2′−kL1
\qquad 利用叠加定理计算得
{ I L f 1 = I L f 1 a b = k L 1 U a b ′ w 0 L f 1 L f 2 ′ ∠ 0 0 = k U a b L 1 L 2 w 0 L f 1 L f 2 ∠ 0 0 I 1 = I 1 A B = U A B j w 0 L f 1 = U A B w 0 L f 1 ∠ − 9 0 0 I 2 = I 2 ′ n = I 2 a b ′ n = U a b ′ n w 0 L f 2 ′ = U a b w 0 L f 2 ∠ 0 0 I L f 2 = I L f 2 ′ n = I L f 2 A B ′ n = k L 1 L 2 U A B w 0 L f 1 L f 2 ∠ − 9 0 0 \left\{ \begin{array}{lr} I_{Lf1}=I_{Lf1ab}=\cfrac{kL_1U_{ab}'}{w_0L_{f1}L_{f2}'}\angle{0^0}=\cfrac{kU_{ab}\sqrt{L_1L_2}}{w_0L_{f1}L_{f2}}\angle{0^0}\\ I_{1}=I_{1AB}=\cfrac{U_{AB}}{jw_0L_{f1}}=\cfrac{U_{AB}}{w_0L_{f1}}\angle{-90^0}\\ I_{2}=\cfrac{I_2'}{n}=\cfrac{I_{2ab}'}{n}=\cfrac{U_{ab}'}{nw_0L_{f2}'}=\cfrac{U_{ab}}{w_0L_{f2}}\angle{0^0}\\ I_{Lf2}=\cfrac{I_{Lf2}'}{n}=\cfrac{I_{Lf2AB}'}{n}=\cfrac{k\sqrt{L_1L_2}U_{AB}}{w_0L_{f1}L_{f2}}\angle{-90^0}\\ \end{array} \right. ⎩
⎨
⎧ILf1=ILf1ab=w0Lf1Lf2′kL1Uab′∠00=w0Lf1Lf2kUabL1L2∠00I1=I1AB=jw0Lf1UAB=w0Lf1UAB∠−900I2=nI2′=nI2ab′=nw0Lf2′Uab′=w0Lf2Uab∠00ILf2=nILf2′=nILf2AB′=w0Lf1Lf2kL1L2UAB∠−900
\qquad 容易推得 { P = U A B ⋅ I L f 1 = L 1 L 2 w 0 L f 1 L f 2 ⋅ k U a b U A B Z i n = w 0 2 L f 1 2 L f 2 ′ 2 L m 2 R a c = w 0 2 L f 1 2 L f 2 2 k 2 L 1 L 2 R a c \left\{ \begin{array}{lr} P=U_{AB}\cdot I_{Lf1}=\cfrac{\sqrt{L_1L_2}}{w_0L_{f1}L_{f2}}\cdot kU_{ab}U_{AB}\\ Z_{in}=\cfrac{w_0^2L_{f1}^2 L_{f2}'^{2}}{L_m^2R_{ac}}=\cfrac{w_0^2L_{f1}^2 L_{f2}^{2}}{k^2L_1L_2R_{ac}} \end{array} \right. ⎩
⎨
⎧P=UAB⋅ILf1=w0Lf1Lf2L1L2⋅kUabUABZin=Lm2Racw02Lf12Lf2′2=k2L1L2Racw02Lf12Lf22
{ G v v = U a b U A B = k L 1 L 2 R w 0 2 L f 1 L f 2 ∠ − 9 0 0 G v i = I 2 I 1 = I L f 2 I L f 1 = U A B u a b = w 0 L f 1 L f 2 k L 1 L 2 ∠ − 9 0 0 \left\{ \begin{array}{lr} G_{vv}=\cfrac{U_{ab}}{U_{AB}}=\cfrac{k\sqrt{{L_1}{L_2}}R}{w_0^2L_{f1}L_{f2}}\angle{-90^0}\\ G_{vi}=\cfrac{I_{2}}{I_{1}}=\cfrac{I_{Lf2}}{I_{Lf1}}=\cfrac{U_{AB}}{u_{ab}}=\cfrac{w_0L_{f1}L_{f2}}{k\sqrt{{L_1}{L_2}}}\angle{-90^0}\\ \end{array} \right. ⎩
⎨
⎧Gvv=UABUab=w02Lf1Lf2kL1L2R∠−900Gvi=I1I2=ILf1ILf2=uabUAB=kL1L2w0Lf1Lf2∠−900
\qquad 从上式看,电压增益和电流增益与负载电阻成线性关系,副边电流滞后原边90度,副变电压滞后原边90度,原副边都是ZPA。从 I o I_{o} Io的表达式看, I o I_o Io与负载大小无关,是恒流输出。
按照其他文献的推导方式也可以推导出这个谐振频率下的Gvi。
统一分析方法
\qquad 文献Load-Independent Voltage and Current Transfer Characteristics of High-Order Resonant Network in IPT System和Unified Load-Independent ZPA Analysis and Design in CC and CV Modes of Higher Order Resonant Circuits for WPT Systems给出了补偿结构的统一分析方法。其基本思路是将wpt系统的去耦模型等效成一个一个的低阶电路
基本低阶等效电路
一阶
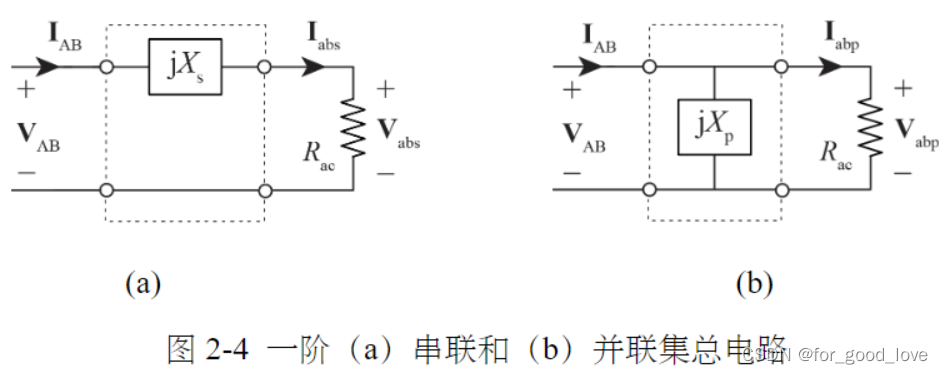
{ V a b p = V A B ( C V ) I a b s = I A B ( C C ) \left\{ \begin{array}{lr} V_{abp}=V_{AB}\qquad (CV)\\ I_{abs}=I_{AB}\qquad (CC)\\ \end{array} \right. {Vabp=VAB(CV)Iabs=IAB(CC)
二阶
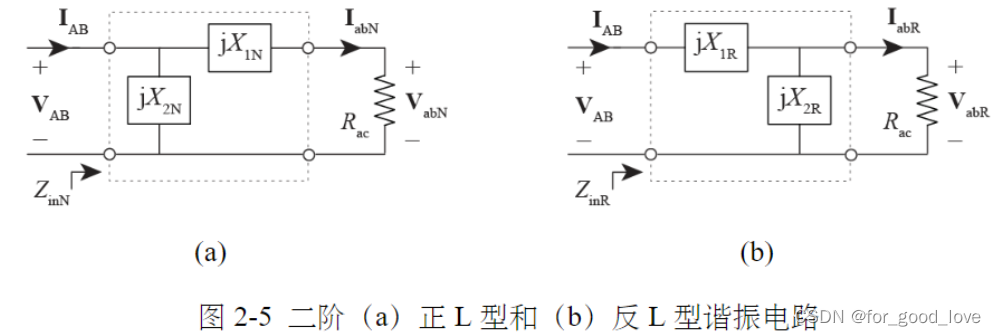
V A B N = { R a c ⋅ j X 2 N R a c + j ( X 1 N + X 2 N ) I A B j X 2 N I A B X 1 N + X 2 N = 0 ( C V ) V_{ABN}=\left\{ \begin{array}{lr} \cfrac{R_{ac}\cdot jX_{2N}}{R_{ac}+j(X_{1N}+X_{2N})}I_{AB}\\ jX_{2N}I_{AB}\qquad X_{1N}+X_{2N}=0(CV)\\ \end{array} \right. VABN=⎩
⎨
⎧Rac+j(X1N+X2N)Rac⋅jX2NIABjX2NIABX1N+X2N=0(CV)
I a b R = { j X 2 R V A B R a c ⋅ ( j X 1 R + j X 2 R ) + j X 1 R ⋅ j X 2 R − j 1 X 1 R V A B X 1 R + X 2 R = 0 ( C C ) I_{abR}=\left\{ \begin{array}{lr} \cfrac{jX_{2R}V_{AB}}{R_{ac}\cdot(jX_{1R}+jX_{2R})+jX_{1R}\cdot jX_{2R}}\\ -j\cfrac{1}{X_{1R}}V_{AB}\qquad X_{1R}+X_{2R}=0(CC) \end{array} \right. IabR=⎩
⎨
⎧Rac⋅(jX1R+jX2R)+jX1R⋅jX2RjX2RVAB−jX1R1VABX1R+X2R=0(CC)
\qquad 上式表明,正L型在电流源作用下可以实现恒压输出,但存在90度相移。反L型在电压源作用下可以实现恒压输出,但存在-90度相移。
\qquad 不论是二阶还是三阶电路,都利用戴维宁定理去分析。
{ Z i n N = ( R a c + j X 1 N ) j X 2 N R a c + ( j X 1 N + j X 2 N ) Z i n R = R a c ⋅ j X 2 R R a c + j X 2 R + j X 1 R \left\{ \begin{array}{lr} Z_{inN}=\cfrac{(R_{ac}+jX_{1N})jX_{2N}}{R_{ac}+(jX_{1N}+jX_{2N})}\\ Z_{inR}=\cfrac{R_{ac}\cdot jX_{2R}}{R_{ac}+jX_{2R}}+jX_{1R} \end{array} \right. ⎩
⎨
⎧ZinN=Rac+(jX1N+jX2N)(Rac+jX1N)jX2NZinR=Rac+jX2RRac⋅jX2R+jX1R \qquad 带入谐振条件
{ Z i n N = ( R a c + j X 1 N ) j X 2 N R a c = − X 1 N X 2 N R a c + j X 2 N Z i n R = R a c ⋅ j X 2 R R a c + j X 2 R + j X 1 R = − X 1 R X 2 R R a c + j X 2 R \left\{ \begin{array}{lr} Z_{inN}=\cfrac{(R_{ac}+jX_{1N})jX_{2N}}{R_{ac}}=-\cfrac{X_{1N}X_{2N}}{R_{ac}}+jX_{2N}\\ Z_{inR}=\cfrac{R_{ac}\cdot jX_{2R}}{R_{ac}+jX_{2R}}+jX_{1R}=\cfrac{-X_{1R}X_{2R}}{R_{ac}+jX_{2R}} \end{array} \right. ⎩
⎨
⎧ZinN=Rac(Rac+jX1N)jX2N=−RacX1NX2N+jX2NZinR=Rac+jX2RRac⋅jX2R+jX1R=Rac+jX2R−X1RX2R
三阶
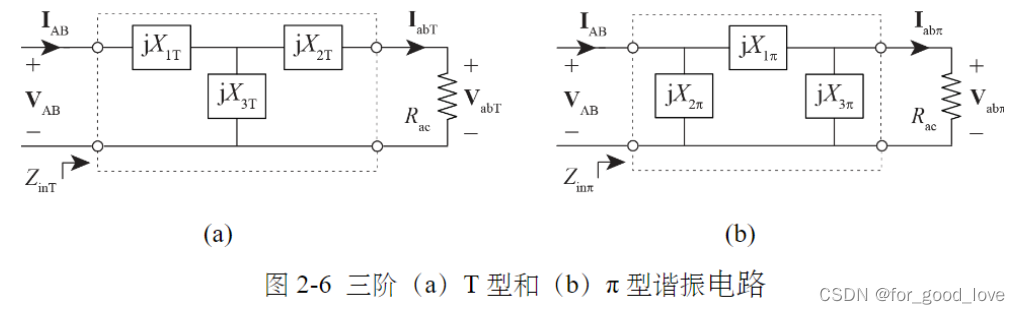
T型 { V a b T = U A B X 3 T R a c j ( X 1 T X 2 T + X 1 T X 3 T + X 2 T X 3 T ) + R a c ( X 1 T + X 3 T ) V a b T = X 3 T U A B X 1 T + X 3 T X 1 T X 2 T + X 1 T X 3 T + X 2 T X 3 T = 0 ( C V ) I a b T = U A B X 3 T j ( X 1 T X 2 T + X 1 T X 3 T + X 2 T X 3 T ) X 1 T + X 3 T = 0 ( C C ) \left\{ \begin{array}{lr} V_{abT}=\cfrac{U_{AB}X_{3T}R_{ac}}{j(X_{1T}X_{2T}+X_{1T}X_{3T}+X_{2T}X_{3T})+R_{ac}(X_{1T}+X_{3T})}\\ V_{abT}=\cfrac{X_{3T}U_{AB}}{X_{1T}+X_{3T}}\qquad X_{1T}X_{2T}+X_{1T}X_{3T}+X_{2T}X_{3T}=0(CV)\\ I_{abT}=\cfrac{U_{AB}X_{3T}}{j(X_{1T}X_{2T}+X_{1T}X_{3T}+X_{2T}X_{3T})}\qquad X_{1T}+X_{3T}=0(CC) \end{array} \right. ⎩
⎨
⎧VabT=j(X1TX2T+X1TX3T+X2TX3T)+Rac(X1T+X3T)UABX3TRacVabT=X1T+X3TX3TUABX1TX2T+X1TX3T+X2TX3T=0(CV)IabT=j(X1TX2T+X1TX3T+X2TX3T)UABX3TX1T+X3T=0(CC)
\qquad 从上式看,在电压源的作用下,三阶T型可以既可以实现恒压,也可以实现恒流输出,实现恒压输出时,输出电压与输入电压同相位;实现恒流输出时,电流超前-90度相位。
Z i n T = { ( R a c + j X 2 T ) ⋅ j X 3 T R a c + j X 2 T + j X 3 T + j X 1 T = j R a c + ( j X 1 T + j X 2 T ) − X 1 T X 2 T − X 1 T X 3 T − X 2 T X 3 T R a c + j X 2 T + j X 3 T j R a c + ( j X 1 T + j X 2 T ) R a c + j X 2 T + j X 3 T X 1 T X 2 T + X 1 T X 3 T + X 2 T X 3 T = 0 ( C V ) X 1 T 2 R + j ( − X 1 T + X 2 T ) X 1 T + X 3 T = 0 ( C C ) Z_{inT}=\left\{ \begin{array}{lr} \cfrac{(R_{ac}+jX_{2T})\cdot jX_{3T}}{R_{ac}+jX_{2T}+jX_{3T}}+jX_{1T}=\cfrac{jR_{ac}+(jX_{1T}+jX_{2T})-X_{1T}X_{2T}-X_{1T}X_{3T}-X_{2T}X_{3T}}{R_{ac}+jX_{2T}+jX_{3T}}\\ \cfrac{jR_{ac}+(jX_{1T}+jX_{2T})}{R_{ac}+jX_{2T}+jX_{3T}}\qquad X_{1T}X_{2T}+X_{1T}X_{3T}+X_{2T}X_{3T}=0(CV)\\ \cfrac{X_{1T}^2}{R+j(-X_{1T}+X_{2T})}\qquad X_{1T}+X_{3T}=0(CC) \end{array} \right. ZinT=⎩
⎨
⎧Rac+jX2T+jX3T(Rac+jX2T)⋅jX3T+jX1T=Rac+jX2T+jX3TjRac+(jX1T+jX2T)−X1TX2T−X1TX3T−X2TX3TRac+jX2T+jX3TjRac+(jX1T+jX2T)X1TX2T+X1TX3T+X2TX3T=0(CV)R+j(−X1T+X2T)X1T2X1T+X3T=0(CC)
\qquad 从表达式上看,不论是恒压输出模式还是恒流输出模式,输入阻抗都不能做到纯阻性
π \pi π型
{ I a b π = j X 2 π j X 3 π I A B j X 3 π ( j X 1 π + j X 2 π ) + j R a c ( X 1 π + X 2 π + X 3 π ) I a b π = X 2 π I A B X 2 π + X 1 π X 1 π + X 2 π + X 3 π = 0 ( C C ) V a b π = j X 2 π X 3 π I A B X 1 π + X 2 π + X 3 π X 1 π + X 2 π = 0 ( C V ) \left\{ \begin{array}{lr} I_{ab\pi}=\cfrac{jX_{2\pi}jX_{3\pi}I_{AB}}{jX_{3\pi}(jX_{1\pi}+jX_{2\pi})+jR_{ac}(X_{1\pi}+X_{2\pi}+X_{3\pi})}\\ I_{ab\pi}=\cfrac{X_{2\pi}I_{AB}}{X_{2\pi}+X_{1\pi}}\qquad X_{1\pi}+X_{2\pi}+X_{3\pi}=0(CC)\\ V_{ab\pi}=\cfrac{jX_{2\pi}X_{3\pi}I_{AB}}{X_{1\pi}+X_{2\pi}+X_{3\pi}}\qquad X_{1\pi}+X_{2\pi}=0(CV) \end{array} \right. ⎩
⎨
⎧Iabπ=jX3π(jX1π+jX2π)+jRac(X1π+X2π+X3π)jX2πjX3πIABIabπ=X2π+X1πX2πIABX1π+X2π+X3π=0(CC)Vabπ=X1π+X2π+X3πjX2πX3πIABX1π+X2π=0(CV)
\qquad 从表达式上看3阶 π \pi π型电路在电流源的作用下,可以实现恒流输出,实现恒流输出时,输出电流与输入电流同相位,实现恒压输出时,电压超前输入电流90度相位。
Z i n π = { ( R a c ⋅ j X 3 π R a c + j X 3 π + j X 2 π ) ⋅ j X 2 π R a c ⋅ j X 3 π R a c + j X 3 π + j X 2 π ⋅ j X 2 π Z_{in\pi}=\left\{ \begin{array}{lr} \cfrac{\left(\cfrac{R_{ac}\cdot jX_{3\pi}}{R_{ac}+jX_{3\pi}}+jX_{2\pi}\right)\cdot jX_{2\pi}}{\cfrac{R_{ac}\cdot jX_{3\pi}}{R_{ac}+jX_{3\pi}}+jX_{2\pi}\cdot jX_{2\pi}} \end{array} \right. Zinπ=⎩
⎨
⎧Rac+jX3πRac⋅jX3π+jX2π⋅jX2π(Rac+jX3πRac⋅jX3π+jX2π)⋅jX2π
\qquad 从表达式上看,CC/CV都无法实现纯阻性输入阻抗.
\qquad 基本的低阶网络可以看出,一阶二阶只存在一个CC或CV点,三阶既存在CC也存在CV点,这很好理解,三阶可以看成是一阶和二阶的级联。
四种基本补偿结构
\qquad 值得注意的是,采用上述分析方法可以得出CC/CV谐振频率,但与上一篇写的CC/CV谐振点不同,这很正常,
Gvv/Gvi分析
\qquad 按照导师的建议,这种补偿网络的是在器件应力、补偿网络复杂性、实现CC/CV复杂性、抗干扰能力等进行折中考虑,导师说重点可以放在参数识别上。使用最简单的SS+参数识别(M的识别可以进行DIPT,R的识别可以实现CC/CV)即可。
SS:
C 1 = 1 w 0 2 L 1 C 2 = 1 w 0 2 L 2 C_1=\cfrac{1}{w_0^2L_1}\qquad C_2=\cfrac{1}{w_0^2L_2} C1=w02L11C2=w02L21
{ I 1 = U a b j w 0 M = U a b w 0 M ∠ 0 0 = U A B R w 0 2 M 2 ∠ 0 0 I 2 = − U A B j w 0 M = U A B w 0 M ∠ 9 0 0 P i n = P o = R e [ U A B I 1 ∗ ] = 1 w 0 M U A B U a b U a b = U A B R w 0 M 带入有: P i n = P o = U A B 2 R w 0 2 M 2 \left\{ \begin{array}{lr} I_{1}=\cfrac{U_{ab}}{jw_0M}=\cfrac{U_{ab}}{w_0M}\angle{0^0}=\cfrac{U_{AB}R}{w_0^2M^2}\angle{0^0}\\ I_{2}=-\cfrac{U_{AB}}{jw_0M}=\cfrac{U_{AB}}{w_0M}\angle{90^0}\\ \end{array} \right. \\P_{in}=P_{o}=Re[U_{AB}I_1^*]=\cfrac{1}{w_0M}U_{AB}Uab\\ U_{ab}=\cfrac{U_{AB} R}{w_0 M}\text{带入有:}P_{in}=P_{o}=\cfrac{U_{AB}^2R}{w_0^2M^2} ⎩
⎨
⎧I1=jw0MUab=w0MUab∠00=w02M2UABR∠00I2=−jw0MUAB=w0MUAB∠900Pin=Po=Re[UABI1∗]=w0M1UABUabUab=w0MUABR带入有:Pin=Po=w02M2UAB2R
{ G v v = U a b U A B = R w 0 M ∠ − 9 0 0 G v i = I 2 U A B = 1 w 0 M ∠ 9 0 0 \left\{ \begin{array}{lr} G_{vv}=\cfrac{U_{ab}}{U_{AB}}=\cfrac{R}{w_0M}\angle{-90^0}\\ G_{vi}=\cfrac{I_{2}}{U_{AB}}=\cfrac{1}{w_0M}\angle{90^0}\\ \end{array} \right. ⎩
⎨
⎧Gvv=UABUab=w0MR∠−900Gvi=UABI2=w0M1∠900
\qquad 按照这个谐振关系进行仿真,从SS的表达式看,当M保持不变时,可以实现恒流输出,电流大小由输入电压大小决定,相位关系是原边电压和原边电流同相位,副变电压和电流同相位,但复变电流超前原边90°。plecs下的仿真结果与计算结果一致。
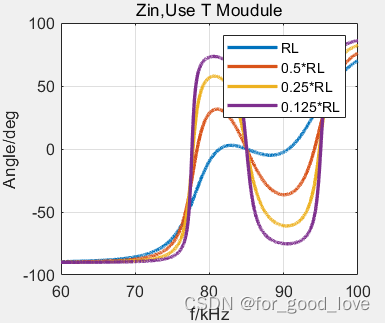
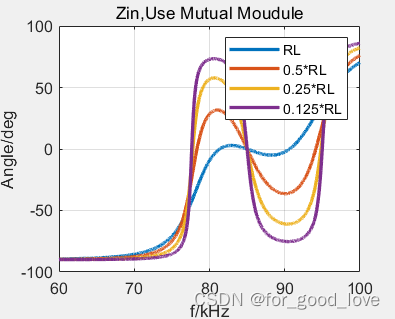
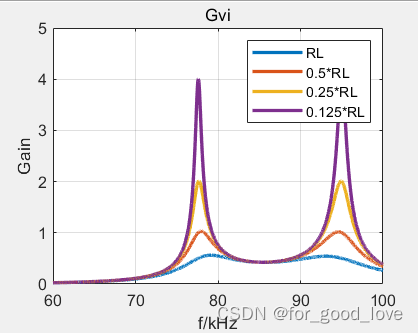
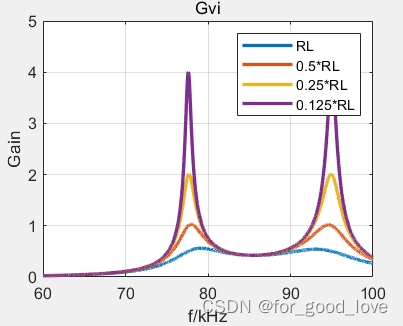
从参数计算的仿真上看,利用M模型和T模型计算出的输入阻抗结果一致。ZPA在额定频率下实现,CC在额定频率下实现,CV有两个点,和CC频率点不一样。从仿真结果可以看出: w c c = 1 L 1 C 1 = 1 L 2 C 2 w c v = 1 ( L 1 − L M ) C 1 ( C 1 = C 2 = 1 w c c 2 L 1 ) w c v = 1 ( L 1 + L M ) C 1 ( C 1 = C 2 = 1 w c c 2 L 1 ) w_{cc}=\cfrac{1}{\sqrt{L_1C_1}}=\cfrac{1}{\sqrt{L_2C_2}}\\ w_{cv}=\cfrac{1}{\sqrt{(L_1-L_M)C_1}}\qquad(C_1=C_2=\cfrac{1}{w_{cc}^2L_1})\\ w_{cv}=\cfrac{1}{\sqrt{(L_1+L_M)C_1}}\qquad(C_1=C_2=\cfrac{1}{w_{cc}^2L_1}) wcc=L1C11=L2C21wcv=(L1−LM)C11(C1=C2=wcc2L11)wcv=(L1+LM)C11(C1=C2=wcc2L11)
LCC
\qquad 按照上诉的谐振条件,按照阻抗计算方式去计算Gvi,Gvv。带入参数计算有
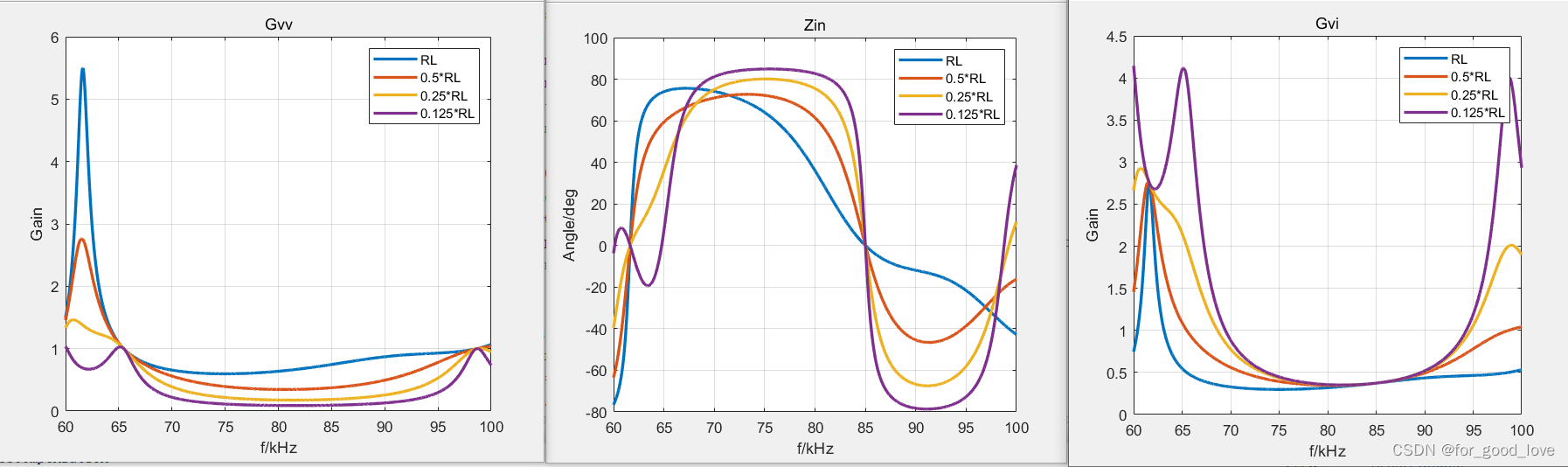
\qquad 值得注意的是,在这个这个谐振参数下,存在其他的CV频率,但无法做到ZPA。其他的CC/CV点计算也很复杂