KMP算法由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。
前言
KMP算法在我看来是一种学起来比较困难但一学会之后就特别简明清晰的算法。
因为其本身的核心思想就并不是太难,所以在看本文的时候不要潜意识的认为算法很难,
尽量用简单的方式去思考,不懂的地方其实多模拟几次就懂了。
再一个就是本人是一个萌新初学者,在一些解释方面可能会出现偏差和错误,请见谅。
我会用我的方式来让读者更快的理解KMP。
问题类型
相信读者在看我的文章时已经或多或少的了解过一些其他的KMP讲解了。
其实这个算法就是为了解决字符串匹配问题,简单来说就是寻找一个字符串里是否包含另一个字符串并可以返回其起始位置,
也可以用来寻找一个字符串中包含几个相同的子字符串,例:
str1=zyzyzyz
str2=zyz
则str1中包含了三个str2,起始位置分别是0,2,4。
KMP其实还有非常多的变式应用,只不过我都不会 这里就不再赘述,请读者自行查阅资料了解。
废话不多说,进入算法讲解部分。
算法讲解
什么是KMP?
KMP就是是一种改进的字符串匹配算法。
我们都知道,普通的暴力是一位一位的挪动字符串并逐位比较,
这样的时间复杂度会达到 O ( n m ) O(nm) O(nm),非常不利。
而KMP则是通过比较操作的简化来优化时间复杂度,不是一位一位的移动,
而是不后退的一段一段的移动,有读者想问:这不会出现遗漏的错误么?
这时候,就需要用到一个移动数组next,KMP算法的核心部分就是next数组的应用,使其时间复杂度大大降低,达到 O ( n + m ) O(n+m) O(n+m)
next数组
next数组的含义
首先要明白next数组是什么——
n e x t [ i ] next[i] next[i] 表示一个字符串前 i i i 个字符的最长的前缀和后缀相同的长度。
⭐其中-1表示无最长的前缀和后缀,0表示1,1表示2,以此类推。
还是不明白?
举个例子:
str=ababc;
next[1]=-1; /none
next[2]=-1; /none
next[3]=0; /a 是最长前缀和最长后缀相同的字符串
next[4]=1; /ab 是最长前缀和最长后缀相同的字符串
next[5]=-1; /none
两个注意点:
- “kkkk” 的最长前缀和最长后缀相同的长度是 3,最长前缀和最长后缀相同的字符串为"kkk"!
- 在“aba”中,ab和ba 不能算作是最长前缀和最长后缀相同!
next数组的求法
知道了next数组的含义之后,就来看看传说中“很难”的求法。
暴力?肯定不行,这样就失去了KMP的意义。
其实,next数组的求法也是 O ( n + m ) O(n+m) O(n+m).
下面我就用图加文字的方式解说next数组的求法。
以字符串"ababc"为例来演示:
k k k 代表当前字符串最长的前缀和后缀相同的长度为 k k k,初始化为-1,见上⭐
i i i 代表当前字符串到了第 i i i 位。
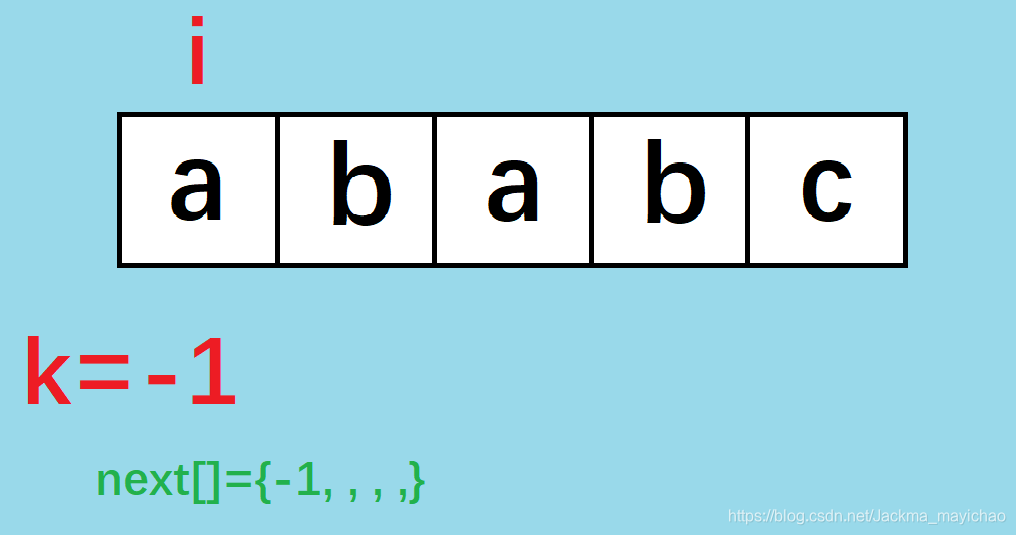
此时字符串“a”没有最长的前缀和后缀相同, n e x t [ 0 ] = − 1 next[0]=-1 next[0]=−1;
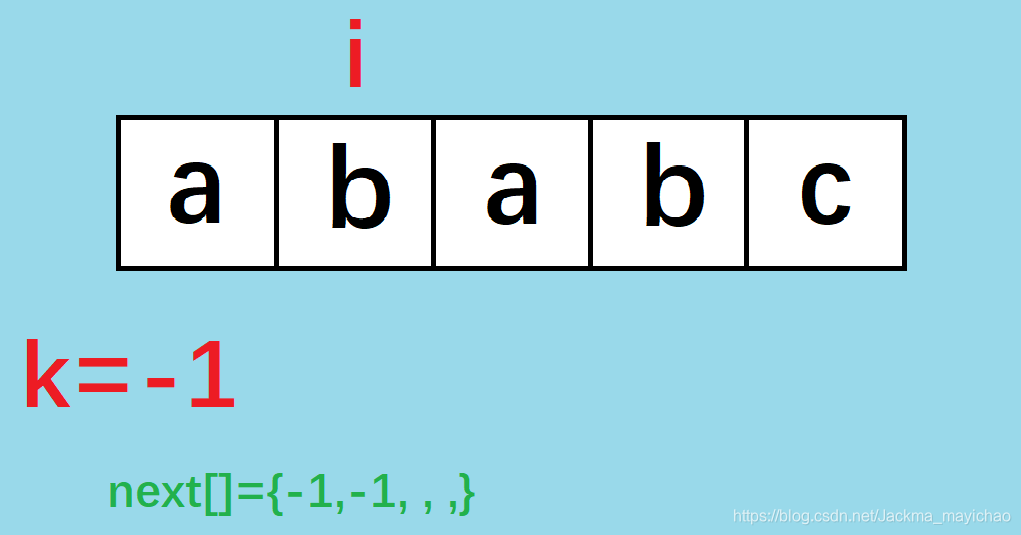
这时字符串"ab"仍没有最长的前缀和后缀相同, n e x t [ 1 ] = − 1 next[1]=-1 next[1]=−1;
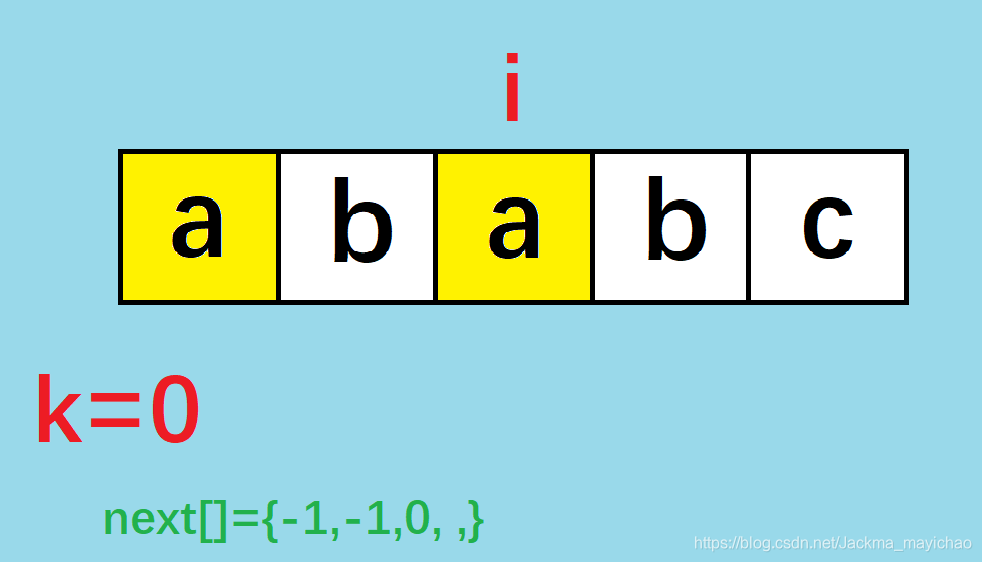
此时 s t r [ k + 1 ] = s t r [ i ] str[k+1]=str[i] str[k+1]=str[i] (这里的K指的是-1,当这一句语句执行之后 k k k 才会 + + ++ ++ 为 0 0 0)
字符串"aba"中 a是最长的前缀和后缀相同的部分。
所以 k + + k++ k++ ,至于为什么是这个判断条件,我在下一张图就详讲。
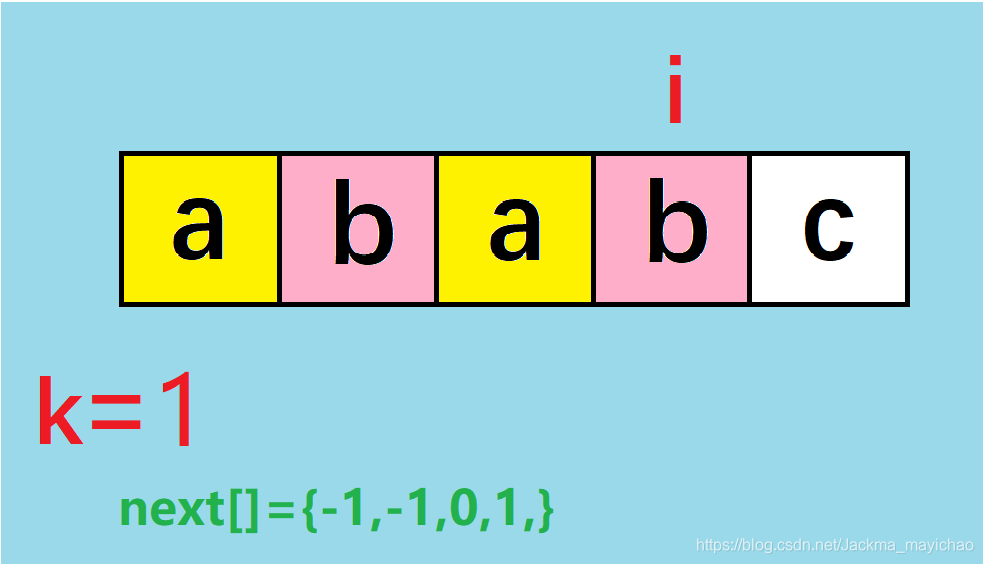
(首先注意:k在判断之后才会等于1,现在等于0!图中直接k=1是为了方便观看)
这个时候,“abab” 字符串中 ab 是最长的前缀和后缀相同的部分。
我们知道,前缀和后缀一定要完全相同才算数,
在现在匹配到的字符之前,我们已经匹配成功了 k k k 个字符,所以如果 k + 1 k+1 k+1 和 i i i 相等,
那么前缀和后缀必然可以匹配。(注意i是循环变量,自己就会 + + ++ ++)
就算 k = − 1 k=-1 k=−1 也没有关系,因为 k + 1 k+1 k+1 作为起点( 0 0 0 是字符串起点)要与某个 i i i 匹配之后才会继续匹配下去,
不然k不会改变,一直是起点。
(这时候要提醒一下,前缀和后缀一定要完全相同才算数!所以一个字符不同,就不能算是最长前缀和最长后缀相同)

重点来了,如果在匹配成功了一段字符串之后突然遇到两个字符匹配失败怎么办呢?
现在 s t r [ k + 1 ] = s t r [ i ] str[k+1]=str[i] str[k+1]=str[i] 匹配失败了!
k − − k-- k−− 再匹配可以吗?
明显不行,因为 0 → k − 1 0\to {k-1} 0→k−1 是已经匹配过的了,就算 k − 1 k-1 k−1 可以与 i i i 匹配,那么也会打乱阵型。
比如:
ababb,当3号位a不能和5号位b匹配时,就算2号位b能和5号位b匹配,总体来看这个字符串还是没有最长的前缀和后缀相同的部分
通过上面的推论,同理可得 1 → k − 1 1\to k-1 1→k−1 都不能与之匹配,那么谁可以尝试与之匹配并不会打乱阵型?
已经匹配成功的k个字符串最长的前缀和后缀相同的部分!
为什么呢?
因为只有让匹配成功的k个字符的 最长的前缀和后缀相同的部分 与之匹配才是符合要求的,其他的字符与之匹配也是白费力气,如同我上面的推论。
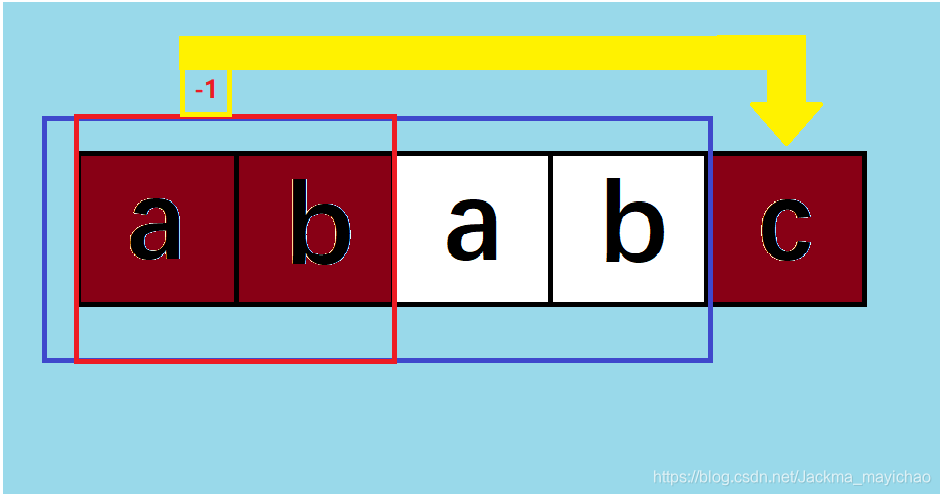
- 重温一下概念: n e x t [ k ] next[k] next[k] 表示一个字符串前 k k k 个字符的最长的前缀和后缀相同的长度。
k个字符串最长的前缀和后缀相同的部分怎么用程序语言表达?———— n e x t [ k ] next[k] next[k] !
所以直接让当前 k = n e x t [ k ] k=next[k] k=next[k] 就可以节省非常多的时间匹配了。
next数组代码实现
void find_next()
{
int k=-1;
for(int i=1; i<=longmbs-1; i++)
{
while(k>-1&&mbs[k+1]!=mbs[i]) //要不断往回找直到找不到为止(k=-1就没有最长的前缀和后缀相同的部分了)
k=next[k];
if(mbs[k+1]==mbs[i])
k++;
next[i]=k; //将当前算出的结果赋给next数组
}
}
当然你也可以不用k=-1去做,用字符数组直接k=0;
void find_next()
{
int k=0;
for(int i=2; i<=longmbs; i++)
{
while(k>0&&mbs[k+1]!=mbs[i])
k=next[k];
if(mbs[k+1]==mbs[i])
k++;
next[i]=k;
}
}
KMP的实现
如果你完全看懂了next数组的求法和 k = n e x t [ k ] k=next[k] k=next[k] 的意义所在,KMP就不是问题了。
我们知道, n e x t [ k ] next[k] next[k] 的实际用途是寻找当前已经匹配的k个字符的最长的前缀和后缀相同的部分。
而KMP刚好是用来寻找一个字符串里是否包含另一个字符串,所以——
可以利用next数组来实现KMP!
这里,我用了一个详细的图来解释KMP,相信你看了之后一定能懂!
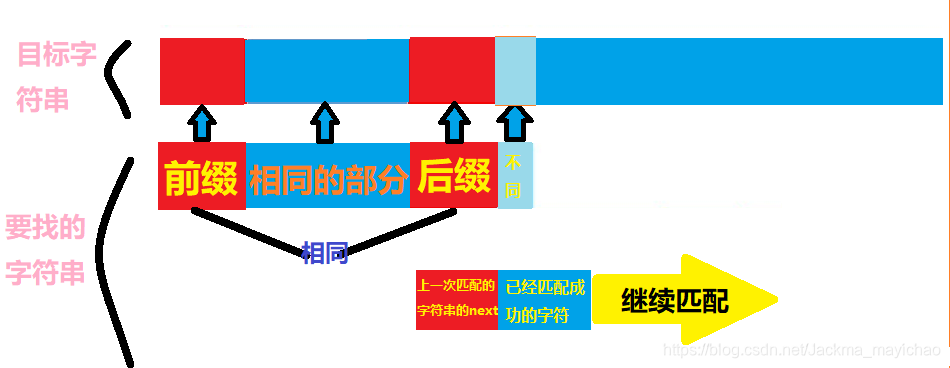
KMP代码
void kmp()
{
next[0]=-1;
find_next();
int k=-1;
for(int i=0; i<=longys-1; i++)
{
while(k>-1&&mbs[k+1]!=ys[i])
k=next[k]; //位移的实现
if(mbs[k+1]==ys[i]) //累计 匹配成功的字符 的个数
k++;
if(k==longmbs-1) //找到了,从当前的k个字符的最长的前缀和后缀相同的部分继续找
{
ans++;
k=next[k];
}
}
}
字符数组版
void kmp()
{
find_next();
int k=0;
for(int i=1; i<=longys; i++)
{
while(k>0&&mbs[k+1]!=ys[i])
k=next[k];
if(mbs[k+1]==ys[i])
k++;
if(k==longmbs)
{
ans++;
k=next[k];
}
}
}
后记
完整KMP代码截这儿
有问题评论区留言,这里推几道题
KMP模板题
KMP题1
KMP题2