End-to-End Object Detection with Transformers（ECCV 2020）

论文链接：论文链接
代码链接：代码链接

摘要

• 动机：传统方法性能受到了NMS、anchor generator等步骤的影响
• 解决方案：DETR使用基于集合的全局损失，通过二分匹配以及transformer encoder-decoder架构进行预测：DETR 预测 目标和全局上下文 的关系以直接并行输出最终的预测集

引言

• 与传统检测器的对比：DETR 一次预测所有object，并使用一组损失函数进行end-to-end训练，该函数在预测对象和真实对象之间执行二分匹配
  
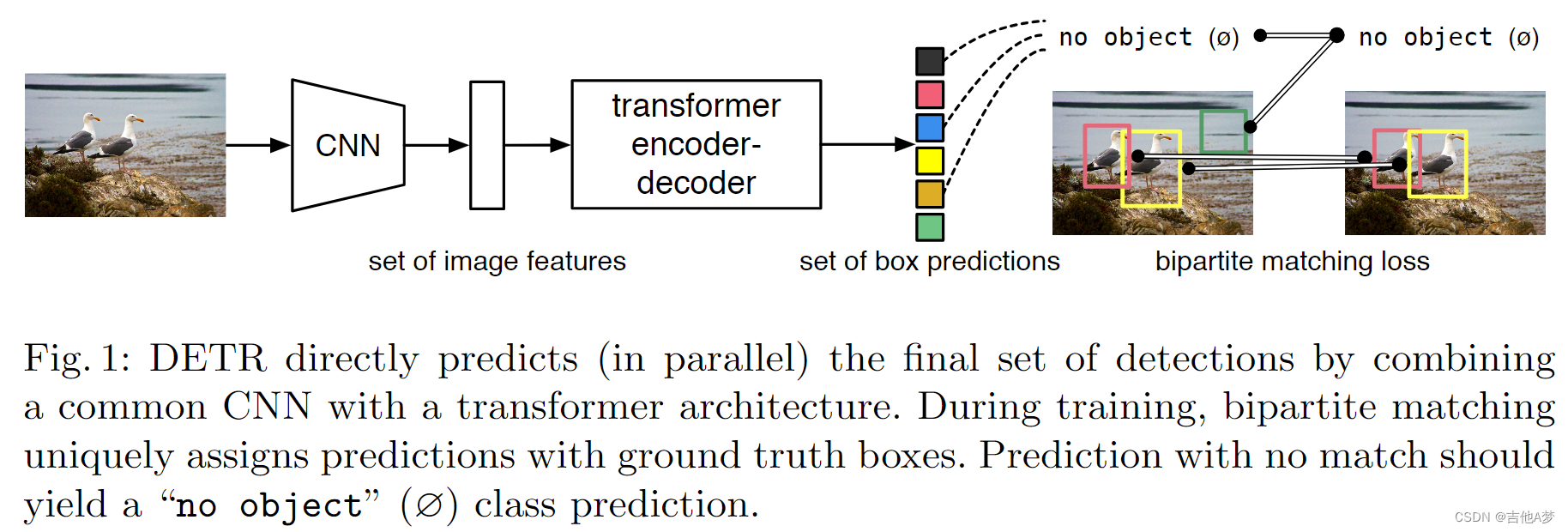
• 与集合预测工作相比：DETR的结合了二分匹配损失 和 基于并行解码（非自回归）的transformer。以前主要是用RNN进行自回归解码。匹配损失函数将预测结果唯一地分配给gt，并且对预测对象的排列组合是不变的，因此可以并行处理

相关工作

集合预测

• 最常见的集合预测任务是多标签分类，其存在的困难是避免重复（例如NMS干的事情），解决这个困难的办法是根据匈牙利算法设计一个损失，找到gt和预测之间的二分匹配（匈牙利算法可以参考链接）

DETR 模型

集合预测损失（Object detection set prediction loss）

• 二分匹配损失： $y$ 是目标的 gt 集合， y ^ = { y ^ i } i = 1 N \hat y=\{\hat y_i\}_{i=1}^{N} y^​={y^​i​}i=1N​ 是 $N$ 个预测值，$N$ 远大于图片中的 gt 个数，同时将 $y$ 视为大小为 N 并用 ∅ 填充的集合（无对象）。为了找到这两个集合的二分匹配，搜索一个具有最低成本的排列（这一部分看不懂的话，看一下匈牙利算法就能理解了，其实就是找一种匹配方法使得匹配损失最小）
  $$\hat{\sigma }={argmin}_{\sigma \in {\mathfrak{S}}_N}\sum _i^N{\mathcal{L}}_{match}(y_i,{\hat{y}}_{\sigma (i)})$$
  其中 $L_{match}(y_i,{\hat{y}}_{\sigma (i)})$ 是gt $y_i$ 和预测索引为 $\sigma (i)$ 的预测框之间的匹配损失
• $L_{match}$：匹配损失考虑了类别预测和 预测框与gt框 的相似性。gt 集合每一个元素 $i$ 可以看做是 $y_i=(c_i,b_i)$ ，其中 $c_i$ 是类标签（可能是 $\varnothing$），$b_i\in [0,1{]}^4$ 是定义 gt 框的中心坐标和其相对于图像尺寸的高度和宽度的向量。对于索引为 $\sigma (i)$ 的预测，将 $c_i$ 类的概率定义为 ${\hat{p}}_{\sigma (i)}(c_i)$，并将预测框定义为 ${\hat{b}}_{\sigma (i)}$，定义 $L_{match}(y_i,{\hat{y}}_{\sigma (i)})$为 − L { c i ≠ ∅ } p ^ σ ( i ) ( c i ) + L { c i ≠ ∅ } L b o x ( b i , b ^ σ ( i ) ) -\mathbb L_{\{c_i\neq∅\}}\hat p_{\sigma(i)}(c_i)+\mathbb L_{\{c_i\neq∅\}}\mathcal L_{box}(b_i,\hat b_{\sigma(i)}) −L{ci​=∅}​p^​σ(i)​(ci​)+L{ci​=∅}​Lbox​(bi​,b^σ(i)​)
• $L_{Hungarian}(y,\hat{y})$:
  
• ${\mathcal{L}}_{box}$：

DETR 结构

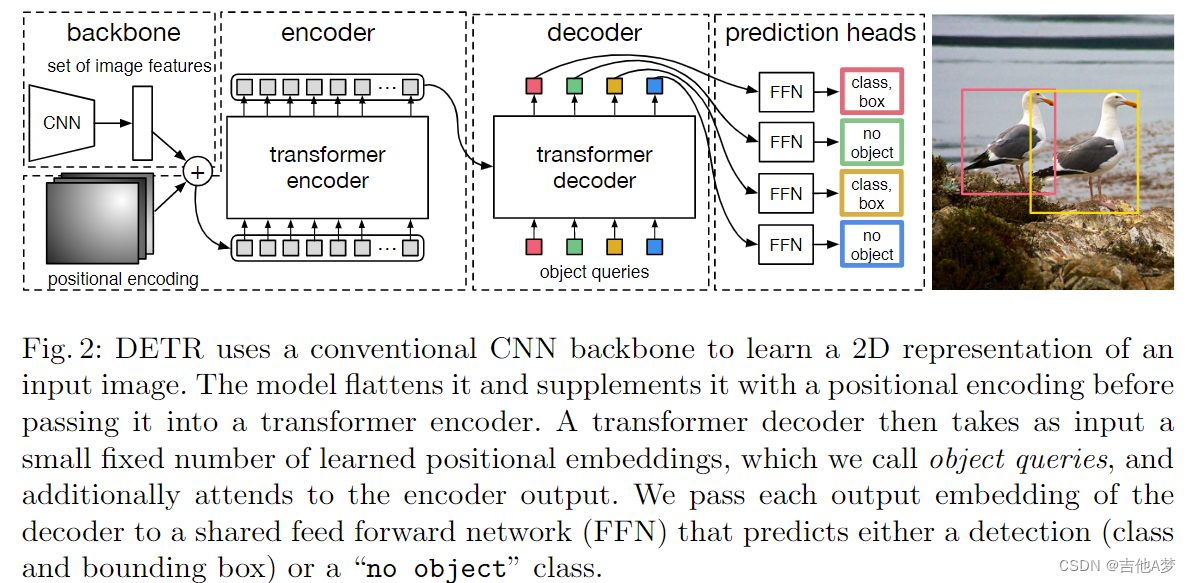
• Backbone：原始图片 $x_{img}\in {\mathbb{R}}^{3\times H_0\times R_0}$，使用一个 CNN 生成特征图 $f\in {\mathbb{R}}^{C\times H\times W}$，典型值为 $C=2048,H,W=\frac{H_0}{32},\frac{W_0}{32}$
• Transformer encoder：
  • $1x1$ 卷积将 $f$ 的通道维度从 $C$ 减少到更小的维度 $d$，得到新特征图 $z_0\in {\mathbb{R}}^{d\times H\times W}$
  • encoder需要一个序列作为输入，因此我们将 $z_0$ 的空间维度折叠为一个维度，从而得到一个 $d\times HW$ 特征图
  • 每个 encoder 层都有一个标准架构，由一个多头自注意力模块和一个前馈网络（FFN）组成。由于 Transformer 架构是置换不变的，我们用固定的位置编码来补充它，这些编码被添加到每个注意力层的输入中
• Transformer decoder：
  • 解码器使用多头自注意机制转换长度为 $d$ 的 $N$ 个嵌入序列。DETR模型在每个decoder层并行解码 $N$ 个对象，而自回归模型一次只能处理一个对象。
  • 往 $N$ 个嵌入序列中加入 positional encoding，并被注意力机制处理。然后通过前馈网络将它们独立解码为框坐标和类标签，从而产生 $N$ 个最终预测。
• Prediction feed-forward networks（FFNs）：
  • 最终预测由具有 ReLU 激活函数和隐藏维度 $d$ 的 3 层感知器和线性投影层计算。
  • FFN 预测 框的归一化中心坐标、高度和宽度。线性投影层使用 softmax 函数预测类标签。
  • 由于我们预测了一组固定大小的 $N$ 个边界框，其中 $N$ 通常远大于图像中感兴趣对象的实际数量，因此使用了一个额外的特殊类标签 $\varnothing$ 来表示在一个范围内没有检测到任何对象。该类与标准对象检测方法中的“背景”类的作用相似

实验

• 对比 Faster R-CNN
  
• encoder 大小的影响
  
• 自注意力可视化图
  
• 每个 decoder 层后的 AP & 稀有类的非分布泛化
  
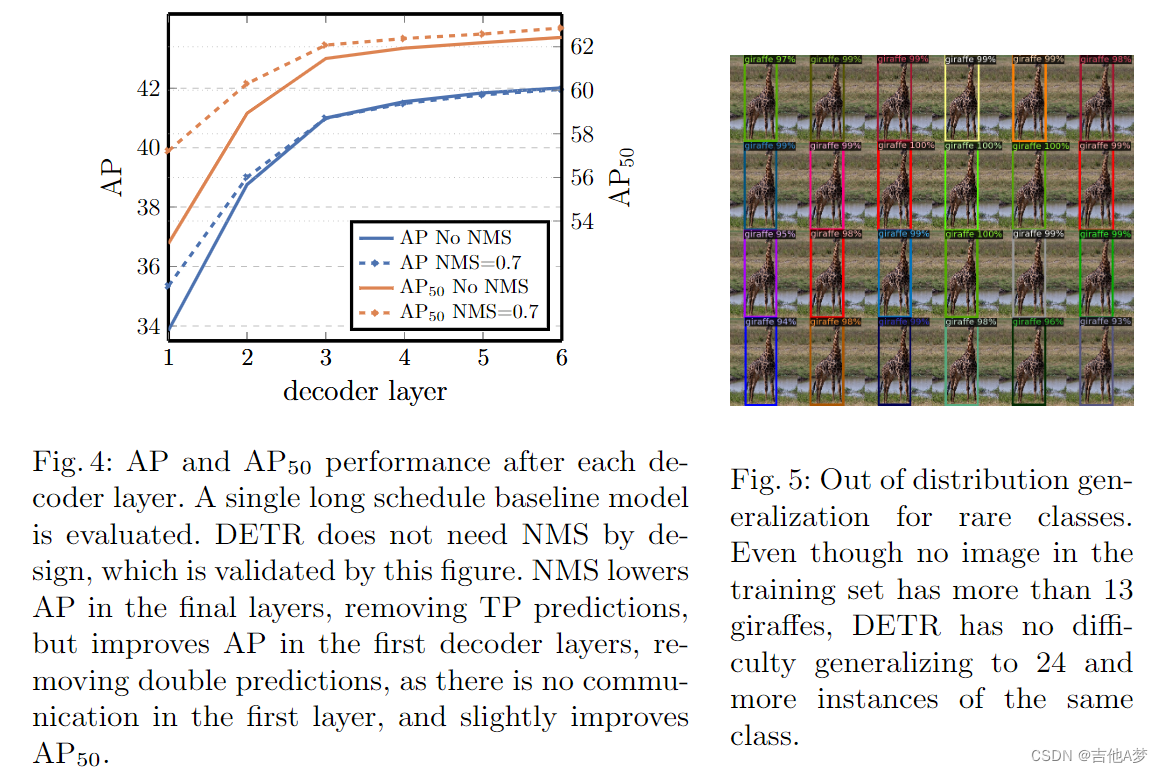
• decoder 注意力在预测对象上的可视化
  
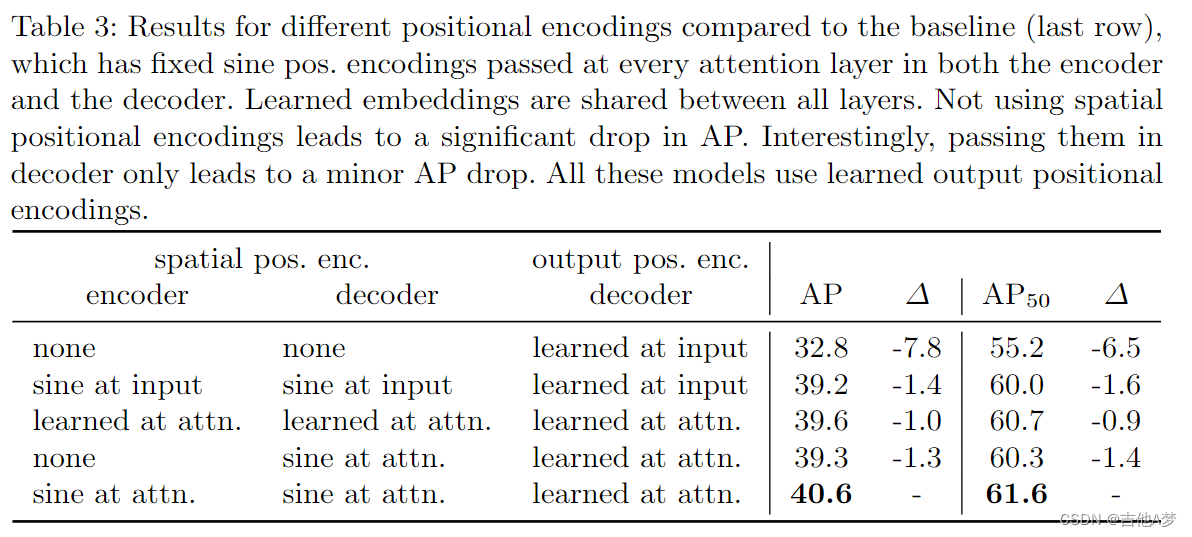
• 不同 positional encoding 的结果
  
• 损失函数对 AP 的影响
  
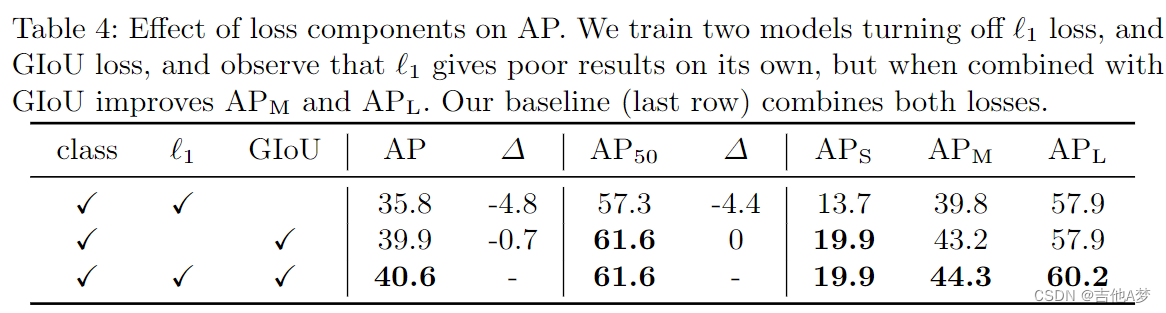
• 框预测的可视化
  
• 全景分割头
  
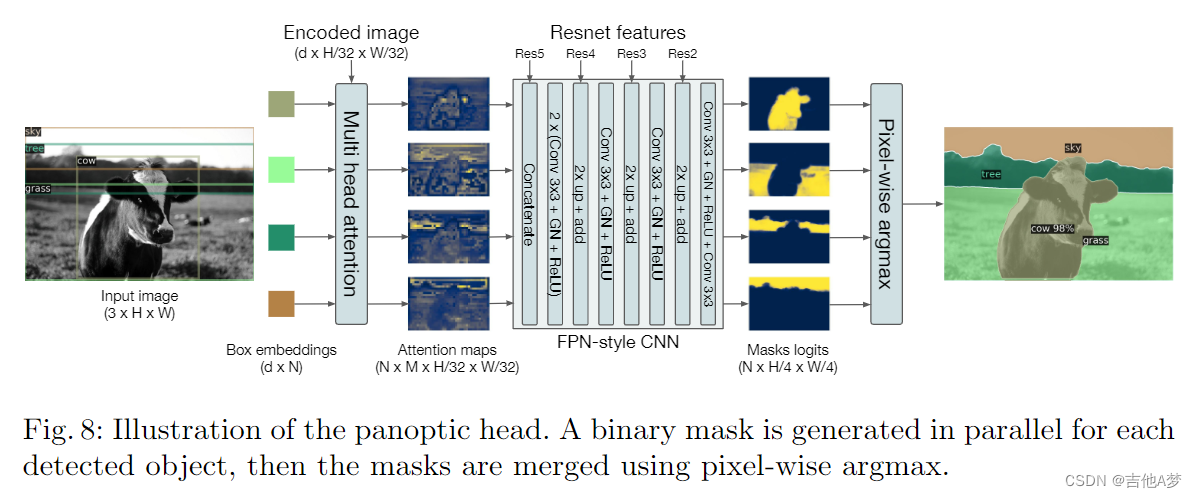
• 全景分割结果
  
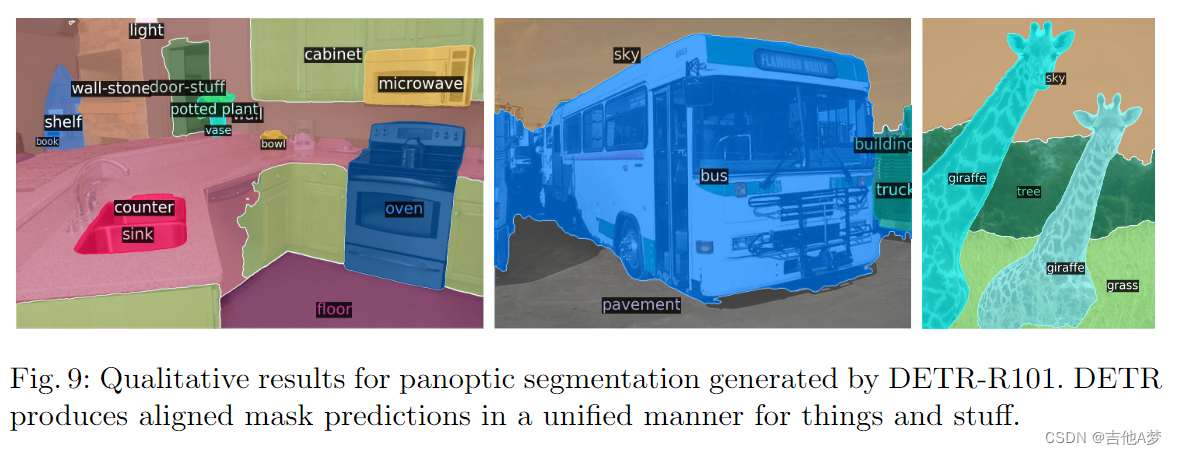
• 全景分割表现
  

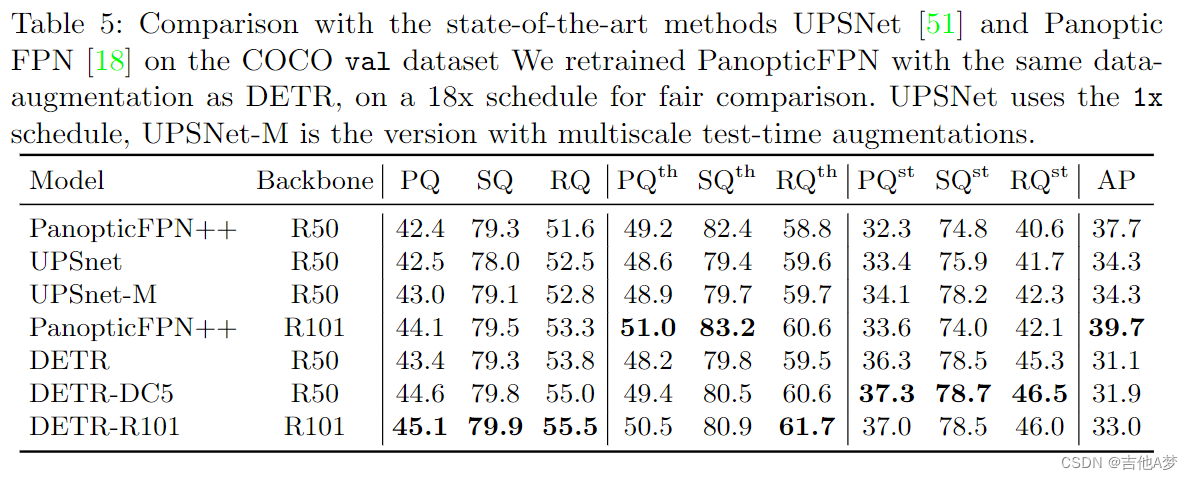
问题

• 二分匹配是什么？
• “匹配损失函数将预测结果唯一地分配给gt，并且对对象的排列组合是不变的，因此可以并行处理”，这句话是什么意思？