[原创]基于Comsol的方形、三角形、椭圆形克拉尼板仿真研究

**起因：**很早就看到过这种能把声波可视化的技术了，但仍然停留在第1次看到时候的震撼当中，也一直在思考这物理层面上是用什么方程来描述的，如果不是方形板，圆形板，三角形板，椭圆形板会是什么样子的呢（网上多看到的是正方形，圆形）。当初水平不够，也只是了解到这是一个平面薄板的弹性体的自由振动n阶模态问题。最近机缘到了，也正式的知道这个方形板叫克拉尼板(chladina plate), 也就有了基于Comsol有限元技术的仿真研究。

1.什么是克拉尼板

克拉尼图形（建议打开这个B站链接感受一下可视化声音的震撼）

【作死物理小讲堂】仅凭振动就能操纵沙子吗？驻波谐振与克拉尼图形 @FPS罗兹 硬核字幕

引百度百科：“十八世纪，德国物理学家恩斯特·克拉德尼做过一个实验，他安放一块较宽的金属薄片，在上面均匀地撒上沙子。然后开始用弓弦拉动，结果这些细沙自动排列成不同的美丽图案，并随着弓弦拉出的节奏的不断增加，图案也不断变幻和越趋复杂——这就是著名的克拉尼图形”，

下图是正方形板仿真中的几个振形:

下图是三角形板仿真中的几个振形:

下图是椭圆板仿真中的几个振形:

1.1 原理

原理：克拉尼板形成的图案是由于板在特定频率下共振，振动波在边界被反射形成稳定的驻波形成的固定波峰波浴。

下面一维绳子的震动就是驻波

2.下面是克拉尼板的各阶振形

下图是用comsol的仿真结果：

3.仿真过程

3.1 仿真套路

下图不管是什么工具基本都划分为前处理、后处理部分，各部分内容如下

3.2 仿真工具

Comsol: 选择Comsol是因为他的安装包大小合适，从力学，热学，光学，流体，波动，电池都能仿真。适合新手学习。软件版权归COMSOL公司所有，文本使用该软件是非营利用途，仅用于知识简谱。

Comsol官方网站：https://cn.comsol.com/

3.3 仿真步骤

3.3.1 建模

我们仿真的图形如下左图是长为40cm*40**0.1cm的正方形薄板(厚度为0.1cm)，且中间是个半径为0.5cm小圆, 由于对称性只需仿真其中1/4即可，这样可以减少计算理，如下图右选择右上角1/4建模即可。

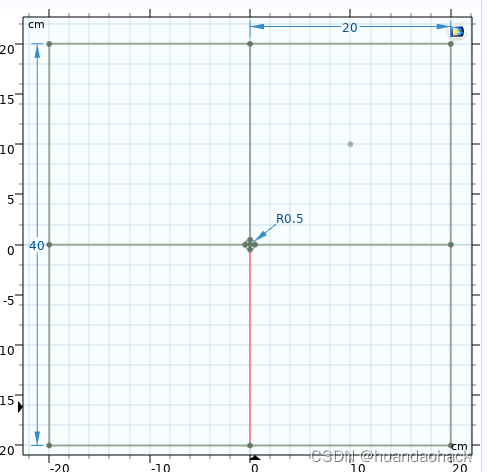
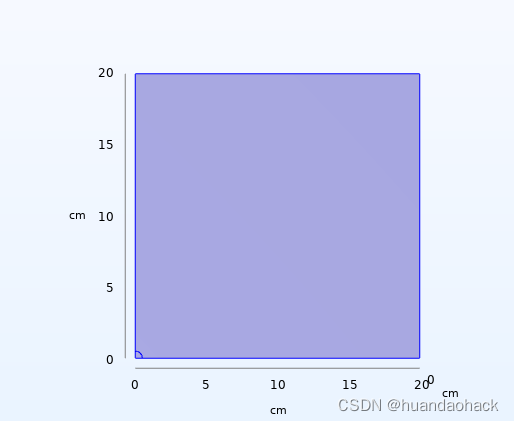
1. 新建“模型向导”，选择“三维”
   
   

2. 物理场选择“结构力学->“壳”,点击添加，研究（这个是结构力学中薄板，即壳的问题）

3. 选择研究的内容，这里研究的是克拉尼板的共振频率问题，所以选择“特征频率”
   

4. 设置模型单位，这里选择cm,因为研究对象长为40cm,并设置参数l为20cm(边长1/2), 小圆半径0.5cm

5. 创建几何模型
   
   

选择XY平台画图

先画1/4圆弧

画右上角1/4正方形

这里就已经完成了几何建模

3.3.2 材料设置

在打开的“内置材料”库选择铝（）材料，克拉尼板基本材料就是铝

把材料分配到模型上

3.3.3 网络设置

网络设计是基于分而治之的思路，实践的模型往往很复杂，不是简单的正方形，三解形，但复杂几何体可以用有限多的正方形，小三角形去逼近，这就是有限元有线的由来。物理方程在正方形，三角形上更易于计算，看图感受理解即可。（网络越细，精度越高，求解时间也越长）

3.3.4 初始条件，边界条件设置

设置薄板厚度，设置好两条边界的对称性， 中间的小圆设置固定（薄板要有支点才不会做自由落体，相当于板中心保持始终不动）

设置好两条边界的对称性：

固定小圆不动：

3.3.5 求解器设置

这步就是要求解我们的问题了，频率扫描范围设置30Hz到5000Hz计算就好。

3.3.6 后处理结果显示

1. 利用对称性画出整个求解结果

利用同样的原理，对“三给镜像1”再做1次镜像就能得到整个40cm**40cm0.1[cm]的正方形了

2. 设置结果图例颜色

到这里就能查看各个共振下板的效果了，有不明白的可以看我上传到B站的视频。

三角形，椭圆形的仿真结果看文末的下载连接。

4.理论分析

参考：《弹性力学》徐芝纶，第十五章薄板的振动问题

自由振动的薄板由下面的微分方程描述：
$$\begin{gathered} D(\frac{{\partial }^{4}w}{\partial x^4}+2\frac{{\partial }^{4}w}{\partial x^2\partial y^2}+\frac{{\partial }^{4}w}{\partial y^4})=0(1) \\ D=\frac{E{\delta }^3}{12(1-\mu )},D为弯曲刚度，E为材料杨氏模量，\mu 为泊松比\delta 为板厚度 \end{gathered}$$

$$\begin{gathered} 对于铝材料，查看相应的材料参数得E=70e9[Pa],\mu =0.33我们仿真的板厚度为1mm,\delta =0.001 \\ 所以D=8.706 \end{gathered}$$

$$\begin{gathered} 对于矩形薄板方程(1)的振形函数解为: \\ {W}_{kn}=sin\frac{k\pi x}{a}sin\frac{n\pi y}{b}自然频率为:\omega ={\pi }^2(\frac{k^2}{a^2}+\frac{n^2}{b^2})\sqrt{\frac{D}{m}} \end{gathered}$$

对于正方形a=b=0.4m，得：
$$W_{kn}=sin\frac{k\pi x}{a}sin\frac{n\pi y}{a}自然频率为:\omega ={\pi }^2(\frac{k^2}{a^2}+\frac{n^2}{a^2})\sqrt{\frac{D}{m}}$$
铝板质量m=0.4x0.4x0.001x2700=0.43千克

当D=8.706 m=0.43 k=1,n=0, a=0.4时计算得, 其图形如下：
$$\omega =3.14^2(\frac{1}{0.4^2}\sqrt{\frac{8.706}{0.4}})=181.82Hz$$

当D=8.706 m=0.43 k=1,n=1, a=0.4时计算得, 其图形如下：
$$\omega =3.14^2(\frac{1+1}{0.4^2}\sqrt{\frac{8.706}{0.4}})=363.64Hz$$

5. 总结

1. 通过本文能了解Comsol在结构力学仿真中的应用及一步骤。
2. 通过本文能学习使用Comsol求解物理对象的共振频率方法。
3. 圆形的网友可以自行研究，对称性越高的物本其共振模式丰富， 正方形>三角形>椭圆

6. 模型下载地址

仿真文件下载地址
仿真操作视频请看我博客