第一部分 --- 范式

1.一个文字即是字句也是短语
1.注意:简单析取式和简单合取式都是由有限个文字组成的 --- 文字是一个单独的命题单元
2.析取范式和合取范式则分别是由有限个短语和有限个字句组成有限个:
3.可以是一个也可以是多个
4.当被括号括起来的时候,我们要将括号内的内容看作一个整体,而不能将括号内的内容分开来看

上面是求解任意一个命题公式的析取/合取范式的步骤

1.当命题变元使得命题公式的析取范式为真的时候,命题公式为真
当命题变元使得命题公式的合取范式为假的时候,命题公式为假
2.命题公式的范式(析取/合取)的表达式不唯一,但是在我们解决问题的时候我们希望范式的表达式唯一,这样子能够对一个问题进行统一的描述,于是人们引入了主范式(析取/合取)
第二部分 --- 主范式
1.短语对应极小项,子句对应极大项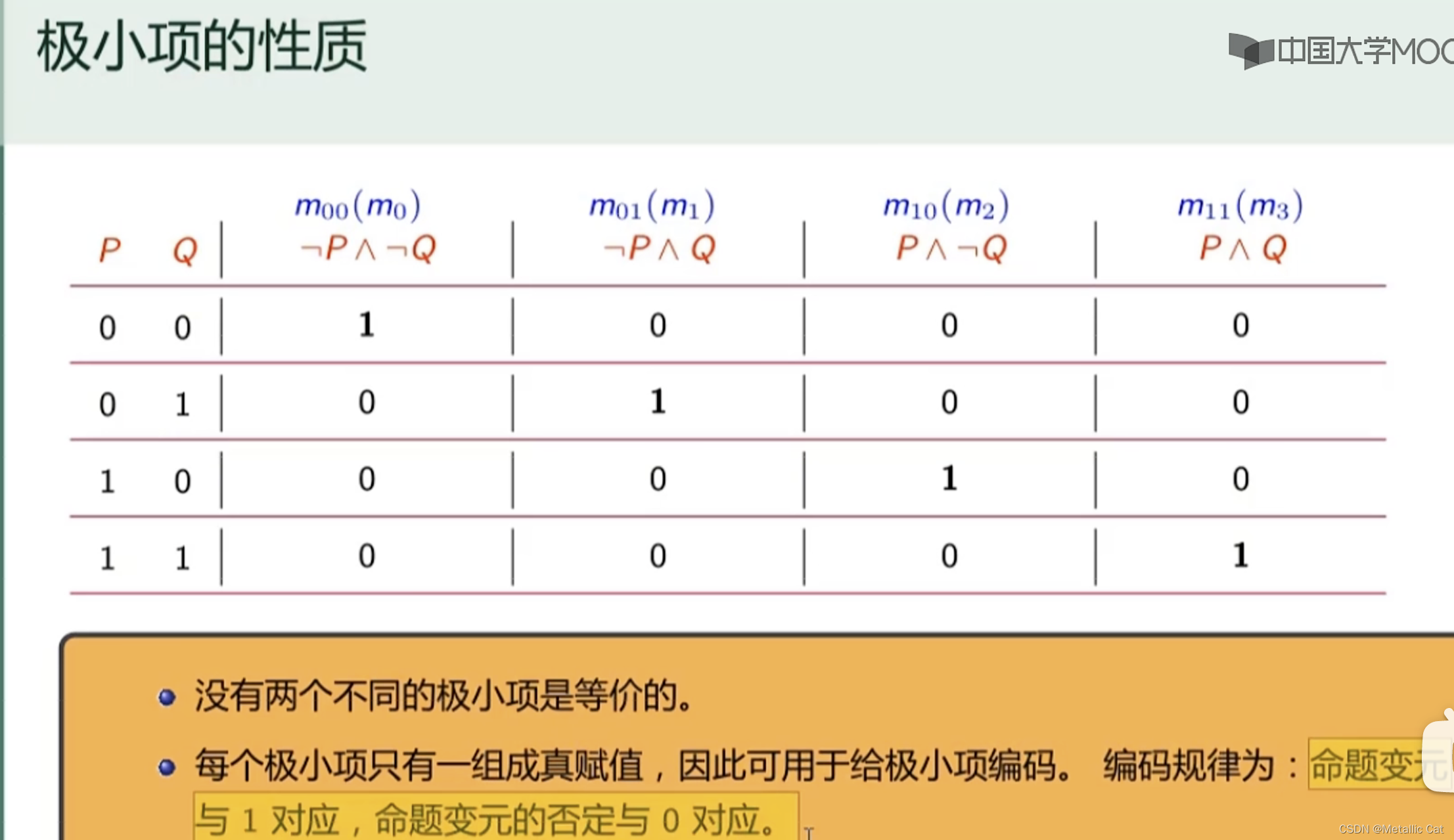
1.给极小项编码的时候用符号m(极小项用小m)+下标表示,且下标有两种表示方法:1.二进制表示法(按照命题变元顺序以及命题变元的值写出对应的二进制码)2.将第一种得到的二进制码转换为十进制表示(极大项同理)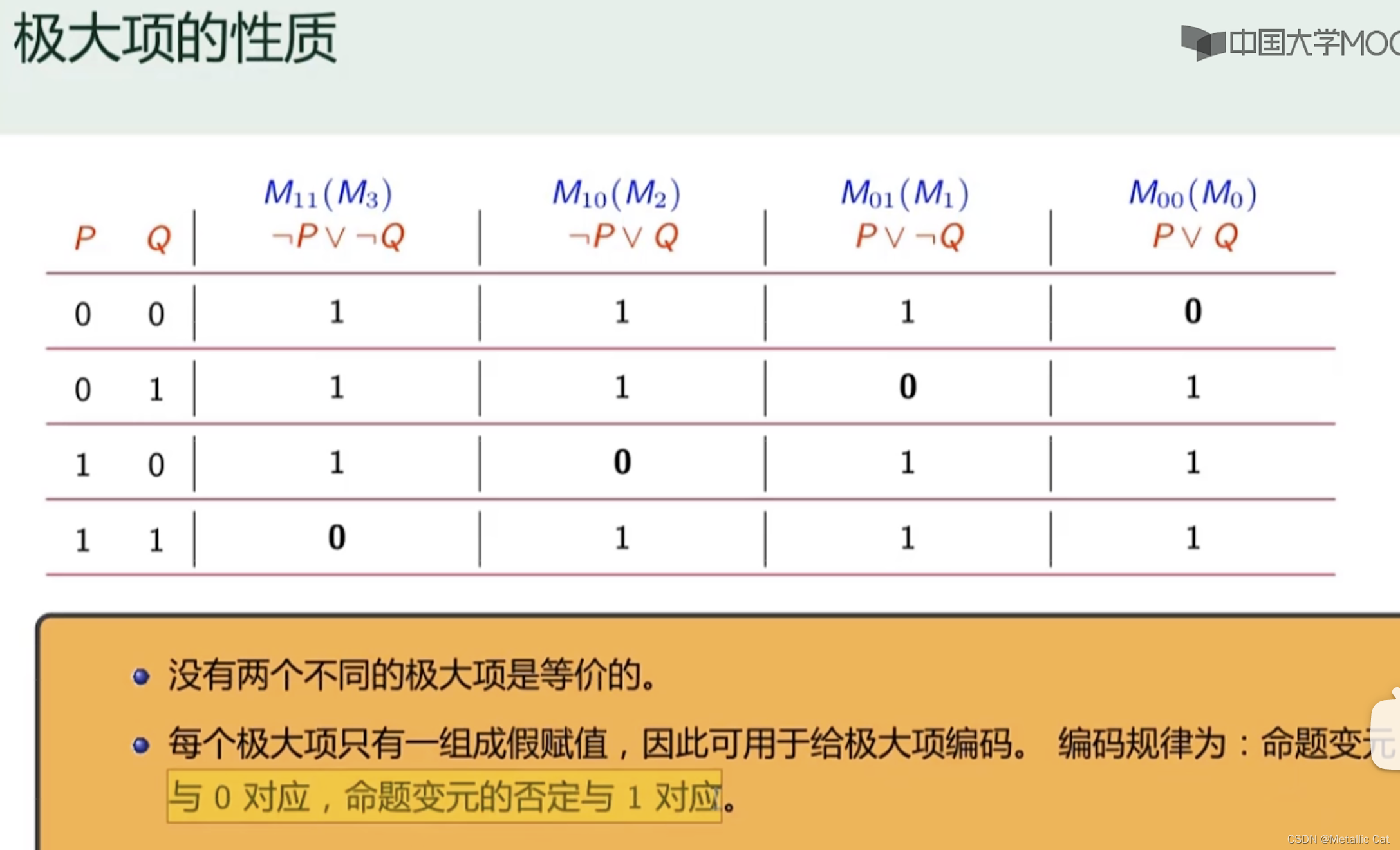
2.极大项用M来表示
3.极小项的下标中出现的0表示的是对应命题变元的否定,1则表示的是对应的命题变元
极小项按照下标编码能够获取到的是短语为真的情况
4.极大项的下标中出现的0表示的是对应命题变元,1则表示的是对应的命题变元的否定
极大项按照下标编码能够获取到的是子句为假的情况

1. 任意两个极小项合取后为0,任意两个极大项析取后为1
2.一个极小项取反后等于对应下标的极大项(极大项同理)
3.所有极大项析取后的结果为0,所有级小项析取后的结果为1
1.为极小项/极大项的条件是:在式子中每个命题变元都要出现,一个命题变元只能出现一次,且命题变元的否定和命题变元不能同时存在
然后当命题变元间都是用析取联结符连接的时候 --- 为极大式
用合取联结符连接的时候 --- 为极小式
求解主范式(析取/合取)的具体步骤如下:

1.最后一步通过交换律将得到的所有极大项/极小项根据下标的大小按照从小到大的顺序排列 
上面这种方法是公式法求解主范式,下面还有一种真值表法求解主范式
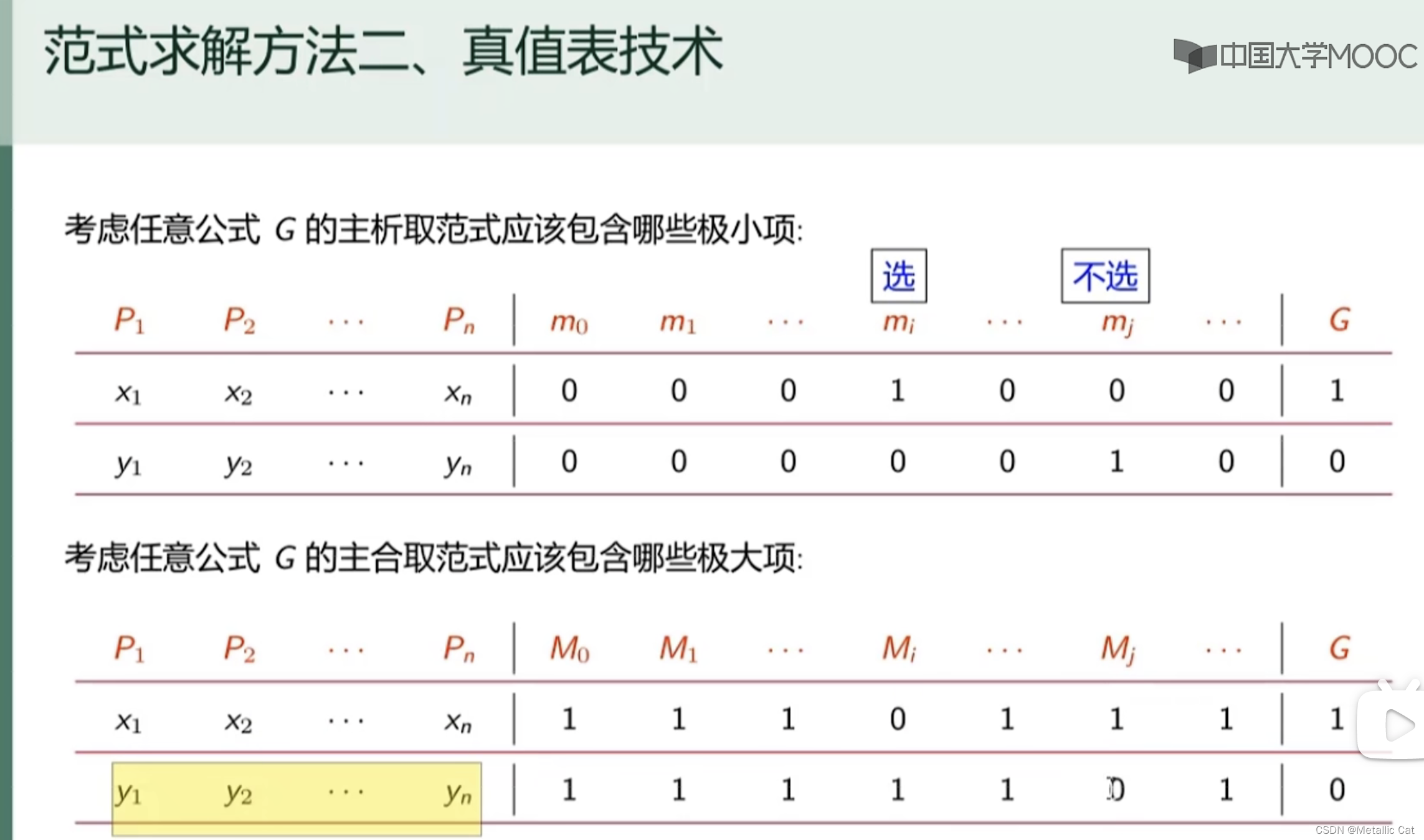
每一个极小项都只在一种命题公式的解释(所有命题变元取确定值后称其为命题公式的解释)下为真,其它命题公式的解释下都为假
每一个极大项则是反过来,它是只在一种命题公式的解释下为假,其它命题公式的解释下都为真
![]()
由上面的真值表技术我们可以得知一个命题公式的极小项合极大项是“互补”的,没有被选中作为极小项的“极小项”其实就是极大项(极大项同理)
根据这个发现我们在求出主析取范式需要的极小项之后,剩下的没被选中的“极小项”就是主合取范式需要的极大项了(反过来也同理)

